电动汽车电机轴断裂的有限元分析

李浩亮 方劲松 林文干 杨超起

东风汽车股份有限公司商品研发院 湖北武汉 430057

1 前言

气候变化、能源和环境问题是人类社会共同面对的长期问题。汽车带给人们方便、快捷和舒适现代生活的同时，也带来了日益增多的交通安全问题、日趋严重的环境污染和潜在的能源危机。汽车的发展时刻面临着安全、环保和节能三大主题。电动汽车由于具有低排放甚至零排放、低噪声和节能等优点，成为当今汽车研究、开发和推广应用的热点之一。开发高性能无污染的电动汽车得到各国政府、汽车制造商、科研院所、风险投资企业的高度重视，他们纷纷制定电动汽车研制计划，掀起全球范围内的电动汽车开发热潮。

在国家政策的引导下，各种类型的电动汽车得到迅速开发并投放到市场上，但由于开发技术不够成熟，会出现与传统汽车迥异的各类失效问题，需要得到快速有效解决。有限元法因其具有高精确度、高可靠性、低成本等优点，成为快速分析和解决电动汽车零部件断裂问题不可缺少的分析工具。

2 电机轴断裂失效情况

一辆电动汽车样车在试车跑道试跑时发生飞车断轴事故，事故描述为：平路车速20 km/h，2挡换3挡过程中，踩离合时出现响声且持续增大，完成换挡到3挡后，响声更大，观察仪表显示转速迅速从2 000 r/min升高到4 500 r/min（满表刻度）,随后换成空挡，几秒钟后发出巨响。整个过程车辆行驶了约20 m，前后历时约8 s，驾驶员一直踩着离合器踏板，没有踩下油门踏板。驾驶员描述响声是电机转速加大形成的声音。

失效描述为：电机轴根部断裂，变速箱一轴断裂成3段，飞轮带离合器飞出，离合器壳被撞裂，飞轮多处撞裂，离合器撞裂解体，主减速器外壳开裂，周边多处被撞变形，动转电机被撞裂。电机轴断口见图1。

图1 电机轴断口（左：飞轮侧；右：电机侧）

电动汽车样车使用的永磁同步电机主要参数见表1。

表1 永磁同步电机的主要参数

金相与失效分析部门对电机轴和变速箱一轴进行失效分析结果为：从断口上看，电机轴是在扭转+弯曲的载荷下发生的一次性快速断裂，有轻微扭转变形痕迹；变速箱一轴的两个断口断面粗糙，有明显的放射纹，宏观上无明显塑性变形痕迹，均为一次性快速断裂断口。电机轴可能是先于变速箱一轴断裂的。

电机供应商对电机轴进行强度校核，计算得出转轴自身可承受最大扭矩为1 188 N m，扭断极限时间为0.8 s（加速时间为0～9 000 r/min）。

按照金相与失效分析分析结果以及断裂过程中驾驶员一直踩着离合器的操作判断，变速箱一轴断裂是后续失效，将不包括在分析过程中，只分析飞轮对电机轴的影响。

3 有限元计算模型

由电机轴尺寸图、电机厂家提供的电机转子的简易CAD模型以及电机总成图纸绘制了电机转轴、转子、飞轮连接法兰的Pro/E模型，并装配上飞轮模型，导入ANSYS Workbench中，如图2所示。

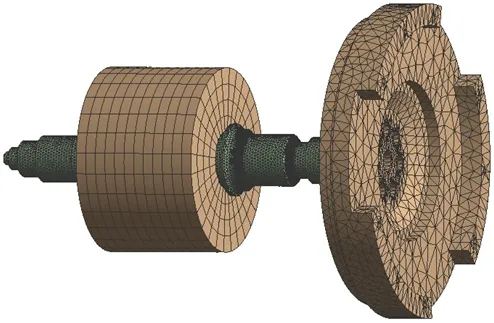
图2 有限元计算模型

电机转子总成重35 kg，转动惯量为0.139 kgm2。电机轴材料为40Cr，抗拉强度为750 MPa，屈服强度为550 MPa，疲劳强度为350 MPa。在有限元模型中通过调整转子的密度和外径达到电机转子总成的质量和转动惯量。飞轮材料为QT450-10，质量为16.4 kg，转动惯量为0.213 kgm2。离合器压盘质量约为15 kg，转动惯量为0.171 kgm2，通过质点单元进行模拟。

4 力矩载荷下的机械应力计算

在电机轴的轴承支撑位置施加圆柱支撑（Cylindrical Support）约束，飞轮的离合器摩擦面上施加1 188 Nm的力矩，转子外径面上施加固定（Fixed Support）约束，如图3所示。计算的等效应力分布见图4，最高等效应力为487 MPa，低于材料屈服强度。

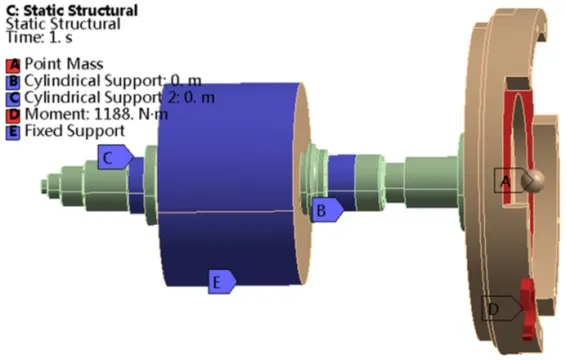
图3 有限元计算模型

按系统设计师提出计算电机加速期间扭矩的分析要求，计算的平均驱动力矩见表2，转轴自身可承受最大扭矩为1 188 Nm是实际驱动扭矩300.8 N m的3.95倍，因此电机轴的静态强度应是足够的。

图4 力矩载荷下的等效应力结果

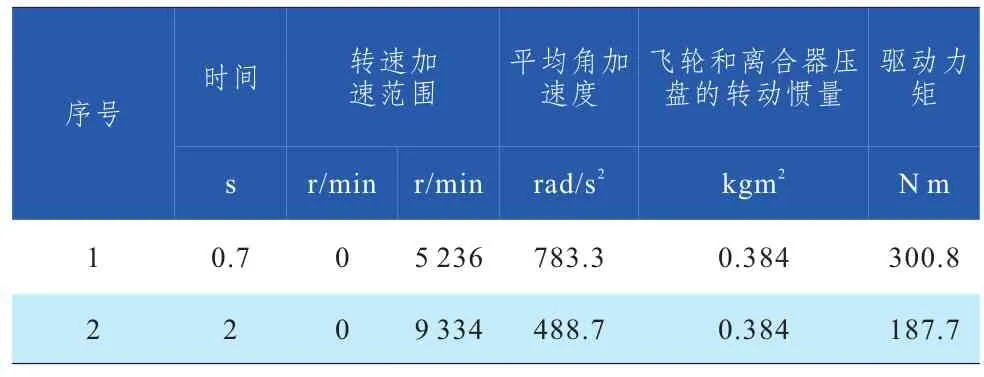
表2 电机加速平均驱动力矩计算结果

5 加速度载荷下的机械应力计算

尽管在电机轴断裂失效时是在平路上行驶，不会有较大的加速度载荷，但为了全面评估电机轴的强度，笔者也进行了加速度载荷下的机械应力计算。在电机轴的轴承支撑位置施加圆柱支撑（Cylindrical Support）约束，在垂向上施加了100 m/s2，转子外径面上施加固定（Fixed Support）约束，计算的等效应力分布见图5，最高等效应力为228 MPa，低于材料屈服强度。

图5 加速度载荷下飞轮壳的最大主应力分布

6 有限元模态分析结果

在电机轴的轴承支撑位置施加圆柱支撑（Cylindrical Support）约束，进行模态分析求取自振频率和模态。模态分析结果见表3，最低弯曲模态频率为111 Hz，模态振型见图6。最低扭转模态频率为208 Hz，模态振型见图7，转子临界转速见图8，最低弯曲模态的1阶临界转速为6 660 r/min，最低扭转模态的2阶临界转速为6 240 r/min。

永磁同步电机的电磁转矩包含基波分量以及2次、6次、12次谐波分量[1]，因此有可能因2次谐波转矩激励而在6 240 r/min附近产生扭转共振。转子的旋转不平衡量是1阶激励，会激励转子弯曲模态共振。扭转共振和弯曲共振的最高模态应力位置与断裂位置一致。

表3 模态频率计算结果

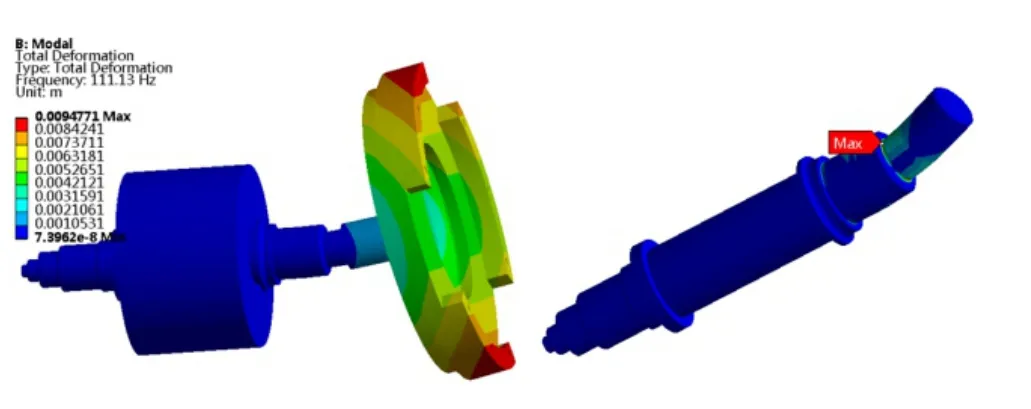
图6 1阶弯曲模态振型和模态应力分布

图7 1阶扭转模态振型和模态应力分布

图8 转子临界转速分布图

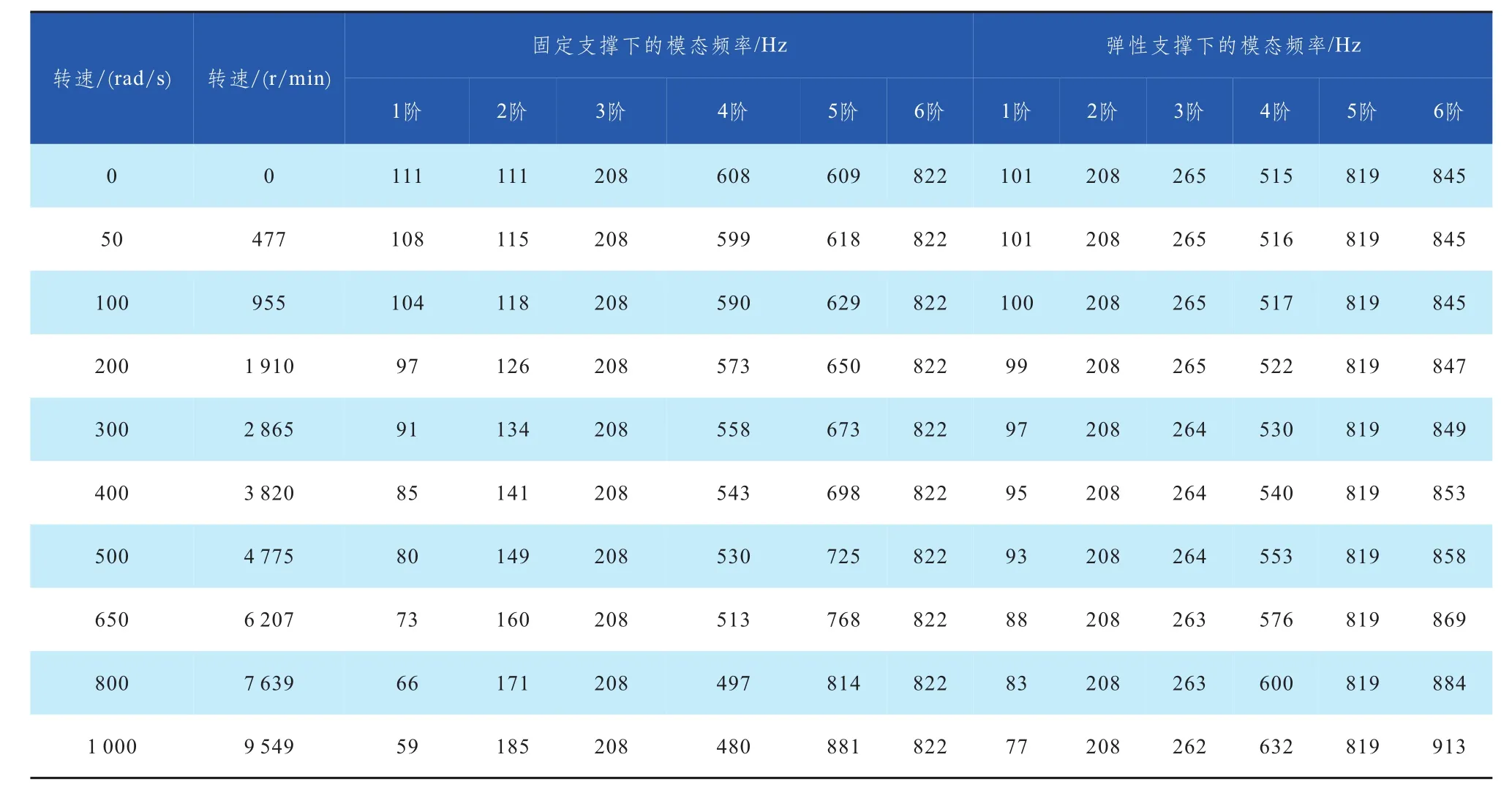
表4 转子动力学模态计算结果

7 转子动力学计算

转子动力学主要研究转子-支承系统在旋转状态下的振动、平衡和稳定性的问题，尤其是研究接近或超过临界转速运转状态下转子的横向振动问题。转子的固有频率除了与转子结构和支撑参数有关外，还随转子涡动转速和自转转速的变化而变化。采用有限元方法计算转子临界转速时，转子会出现正进动和反进动。由于陀螺效应的作用，随着转子自转角速度的提高，反进动固有频率将降低，而正进动固有频率将提高。根据临界转速的定义，在对永磁电机转子临界转速进行分析时应只分析其正进动的固有频率[2]。

ANSYS Workbench中的转子动力学计算是在模态分析的Analysis Setting中将Damped设为Yes，Coriolis Effect设为On，Campbell Diagram设为On，如图9所示。Number of Points设为10则将计算10个转速，加入边界条件Rotational Velocity，指定计算的旋转速度表格。

考虑到实际轴承支撑的弹性对转子的固有频率有影响，因此进行了固定支撑和弹性支撑的转子动力学计算。固定支撑是用Cylindrical Support约束；而弹性支撑则是删除Cylindrical Support约束，在Connections下用Bearing弹性单元代替，单元刚度设为380 000 N/mm[3]，如图9所示。

转子动力学计算的前6阶模态频率结果见表4，计算的固定支撑下的临界转速图见图10，弹性支撑下的临界转速图见图11。计算结果表明，旋转速度和支撑参数对转子系统的弯曲模态频率有较大的影响，但是对其扭转模态频率没有影响，仍然与模态计算结果相同。由于不考虑反进动的固有频率，则在低于9 000 r/min的转速范围内没有1阶弯曲临界转速。

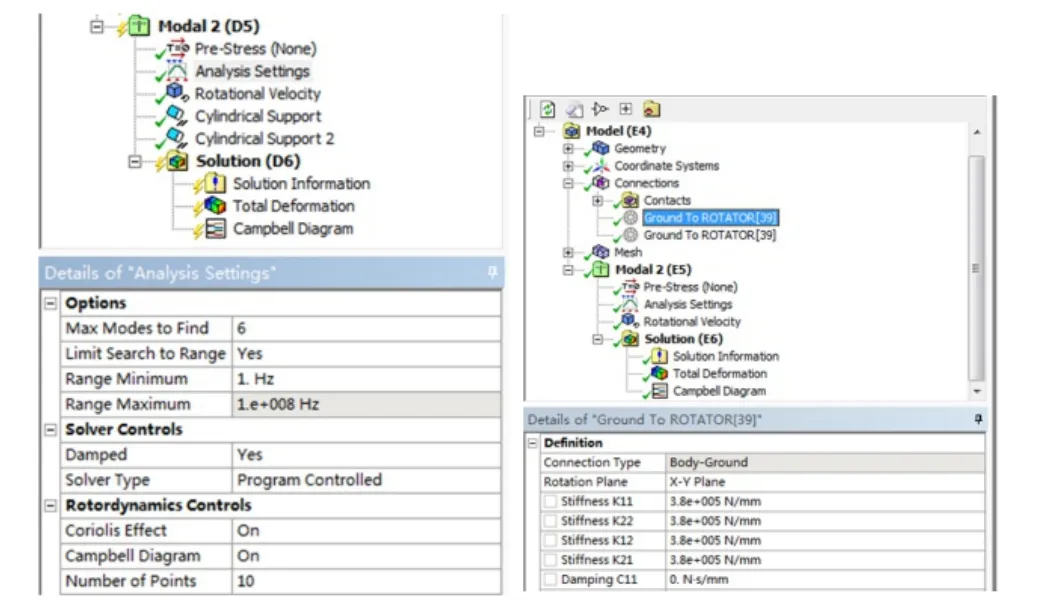
图9 转子动力学计算的分析设置（左：固定支撑；右：弹性支撑）

8 结语

a.电机加速过程中平均驱动力矩为300.8 N m，而电机轴的驱动能力大于1 188 N m，因此电机轴的静强度应该是足够的；

b.在100 m/s2的加速度载荷下，电机轴的最高等效应力为228 MPa，低于材料的屈服强度；

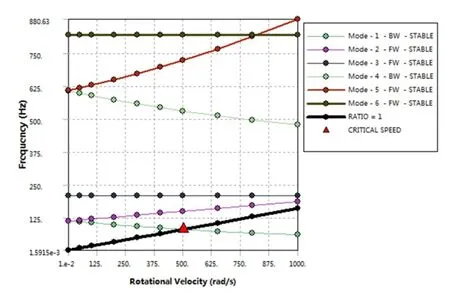
图10 固定支撑下的临界转速

图11 弹性支撑下的临界转速

c.电机转子-飞轮系统的最低弯曲模态频率为111 Hz，会在6 660 r/min左右产生弯曲共振；

d.电机转子-飞轮系统的最低扭转模态频率为208 Hz，会在6 240 r/min左右产生扭转共振；

e.转子动力学计算中，旋转速度和支撑参数对电机转子的弯曲模态频率有较大的影响，但是对其扭转模态频率没有影响。

基于有限元分析结果，电动机轴断裂失效的原因应是由于电动机转速超出设计规范要求的4 200 r/min的最高转速，达到系统的临界转速而产生扭转共振和弯曲共振导致电动机轴断裂。

因为电机没有内燃机的四冲程工作产生的转速波动，而且电机转子本身的转动惯量较大，与大惯量的飞轮形成双扭摆振动系统的自振频率较低，产生共振时就会损坏电机轴，因此建议降低电机传动系统的飞轮转动惯量和质量；或者增大电机轴直径，提高系统模态频率，防止产生转子共振。

依据最小设计变更的要求，采取在电动机控制软件中加入防止电动机超速的控制策略的措施，在后续可靠性试验和售后市场中再未出现此类失效。