登高平台消防车曲臂连杆的铰点优化及强度分析
2021-01-29周轶群张萧笛
周轶群 张萧笛
长沙中联消防机械有限公司 湖南长沙 410200
1 前言
登高平台消防车是常用于高空消防救援的主要装备之一。随着城市高层建筑数量和高度不断增加,高空消防救援工作对登高平台消防车最大工作高度和救援车辆稳定性要求也在不断提高,对登高平台消防车的臂架长度和轻量化设计提出了更高要求[1-2]。
为了在安全设计范围内增加工作高度,在结构设计中需要尽可能地减少臂架上零部件的质量。目前常见的设计方法是利用有限元分析软件,结合零部件工作时的应力分布情况,最大限度地挖掘材料潜力,对结构进行优化,降低结构件的质量[3-5]。如伍财生等人将有限元法应用到臂架的静力学分析和模态分析中,对臂架的静动态特性和臂架截面的参数优化进行了研究,实现了登高平台消防车臂架结构的轻量化设计[6];葛广成应用机械系统动力学仿真软件(ADAMS)对登高消防车的臂架进行受力分析,为整车的稳定性提供了理论指导和设计依据[7]。另外,通过优化臂架运动传动连杆机构,也可减少臂架机构在运动中结构件的最大应力值,这种优化技术多用于多臂架结构的混凝土泵车,如龚桂良等采用Solidworks Motion的优化设计模块对直杆式6铰点连杆机构进行优化,以此改善了变幅油缸和直杆式6铰点连杆机构的力学性能[8];宋晶晶通过建立臂架系统驱动机构的优化模型,并基于遗传对该优化模型进行了求解,极大地减小了臂架系统上最大驱动力的值[9]。同样国外也有许多已将优化技术应用于不同产品的臂架系统设计中的实例[10]。
本文通过对消防车曲臂变幅机构进行力学分析,建立了与之对应的连杆机构的铰点优化数学模型,利用遗传算法编制计算程序对其不同边界条件下的铰点布置进行优化求解,并对臂架强度进行有限元分析与试验验证。
2 连杆铰点力学模型的建立
以某登高平台消防车上的曲臂旋转变幅的连杆机构为例,图1(a)所示是由曲臂、主臂、连杆1、连杆2所组成的四连杆机构。图1(b)所示为变幅油缸直线伸缩运动为曲臂相对主臂的转动提供动力。为了便于力学分析与计算,对该连杆机构进行简化和标定,简化示意图如图1(c)所示,其中将铰点P3在坐标轴中定为原点。在连杆机构的设计中,各连杆上铰点之间相对位置的布置不同,将影响曲臂在运动过程中变幅油缸的推力大小。
为了便于力学分析,设曲臂连杆机构在运动时,曲臂的空间相对位置将始终保持在水平状态。图1(b)中,铰点P3处的载荷可简化为曲臂部分重力mg在连杆机构中产生的弯矩M(包含了曲臂末端其他结构质量和工作斗载荷)。在力学分析公式中,设Lij为铰点之间的几何矢量,Fi表 示铰点Pi处连杆之间的矢量力。
设逆时针方向弯矩为正,根据力和力矩之间关系,列出以下平衡方程:
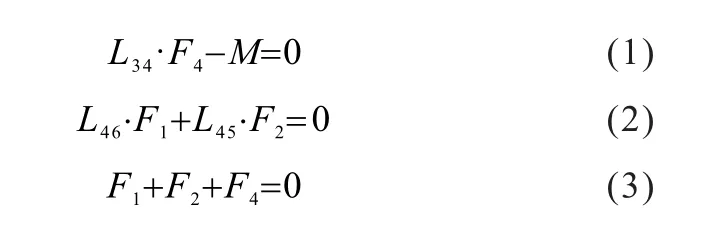
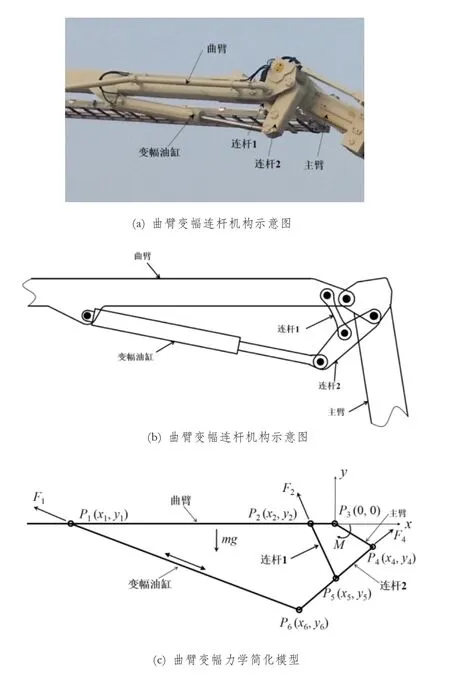
图1 曲臂变幅连杆机构

式中,X为曲臂变幅连杆机构中各铰点坐标位置;θ为主臂与曲臂之间的相对转角;f(θ,X)为转角θ与铰点坐标之间的函数关系表达式,表示把弯矩M与油缸支撑力F1联系起来。在此力学模型中,臂架全收回时θ=0,图2所示状态即为全收回状态。
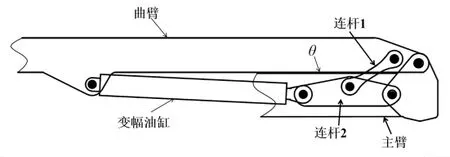
图2 臂架连杆机构全收回状态
为了改善变幅油缸的受力情况,减小铰点上的应力分布,以下选择以油缸在变幅过程中的最大支撑力最小化为优化对象,目标函数则有:
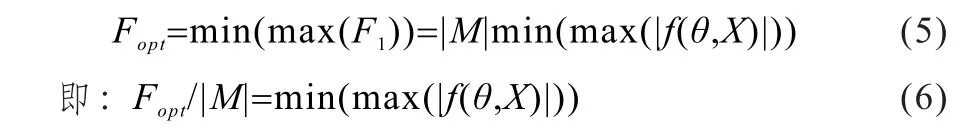
由式(6)可以看出,可用最大油缸力与所加弯矩之比,即输入输出之比来表征连杆机构上铰点布置的力学状态。
从式(4)中可以看出,油缸支撑力F1与铰点P3处弯矩M成正比关系,油缸支撑力最大时的出现状态与载荷无关,只与主臂曲臂的相对位置有关,因此在载荷大小不定的情况下,加载一定单位的力就可进行优化计算。从式(4)中也可以看出,臂架在往返运动过程中,在夹角θ相等的状态下,油缸的支撑力大小是相等,因此在往返运动过程中,在优化推力的时候,也同时优化了拉力。
3 连杆铰点的边界条件
在已知优化的目标函数后,还需确定优化模型的约束边界。在臂架系统的连杆机构设计中,为了满足产品功能需求和连杆形成的基本条件,连杆机构中的每个铰点位置都会被限定在一定的范围内。在图1(b)中,曲臂是在油缸L16和 连杆1L25的推力或拉力的共同作用下运动的,故此为了防止连杆铰点P6不能越过铰点P1和铰点P4的连线,铰点P2和铰点P5的连线不能越过铰点P3,否则连杆机构存在死点,根据右手螺旋法则有以下约束条件:

如果考虑到构成连杆机构的条件和轴套之间的最小距离,为了保证铰点处受力时的强度,铰点处的轴及轴套的最小半径Rmin必须要大于一个值,如图3所示。
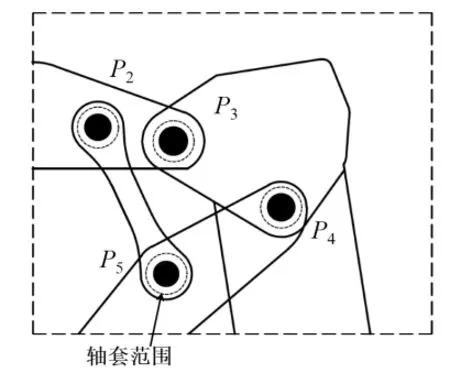
图3 轴套限制示意图
即铰点之间需要要满足式(9)~(12)的约束条件,通过该 约 束 条 件 还 可 以 判 断 铰 点P2、P3、P4、P5是 否 组 成 四 连杆机构。


在臂架系统连杆机构设计的方案阶段,为了满足产品开发中功能与外观设计的要求,设计时一般会希望优化后的铰点位置是在初始方案铰点附近的一定范围内进行变化的,这个范围可用如图4中所示的方形边界表示。如铰点P1满足式(13)、(14)的方形边界限制。同时为满足臂架的功能性要求,臂架之间的相对夹角θ必须满足式(15)。其他铰点按照设计要求,施加相应的方形边界约束。
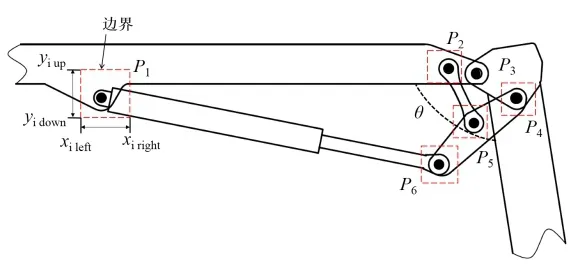
图4 铰点方形边界约束
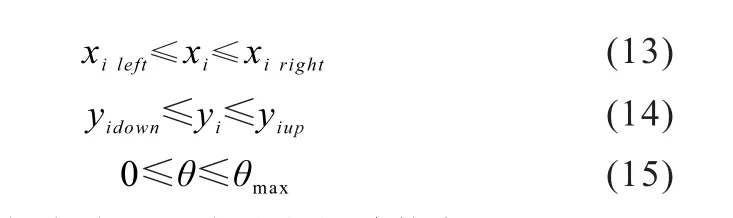
式中,θmax为主臂与曲臂之间的最大相对转角。
在臂架连杆的运动中,铰点P5和铰点P6的位置应位于臂架的下端面以下,同时要考虑到连杆2销轴边界与曲臂下端面的最小距离,故铰点P5和铰点P6只能出现在曲臂下端面所构成的包络线之间,如图5所示。通过描点使用样条曲线插值的方法即可求得包络线拟合曲线的方程,即铰点的位置应满足以下约束公式:

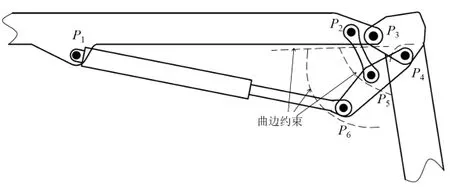
图5 铰点曲线边界约束
对于臂架连杆机构中的油缸,臂架在运动过程中,油缸的伸长量随着夹角θ的变化而变化,且在优化过程中铰点位置的调整也会引起油缸尺寸的变化,但是受油缸自身特性的影响,油缸存在死程限制条件,故此油缸的最小安装距离必须满足最小值约束,即当L16最小时,都要大于油缸伸缩行程s一定的最小死程尺寸b,式(17)中最小死程尺寸b的大小由油缸结构特性所决定。

4 优化结果
由于遗传算法仅需知道目标函数的信息,而不需要其连续可微等要求,因而具有广泛的适应性,在很大程度上可以跳出局部最优解找到全局最优解[11-13],故在编制曲臂连杆机构优化程序时,选用遗传算法求解。结合式(1)~(4)和式(7)~(17)这些铰点的边界约束条件和优化目标函数式(6),在初始条件中,曲臂变幅最大角度θmax= 175°,油缸死程为260 mm,设曲臂载荷在铰点P3处的弯矩M恒为120 kNm。表1中为连杆机构中初始坐标与优化计算后的结果。
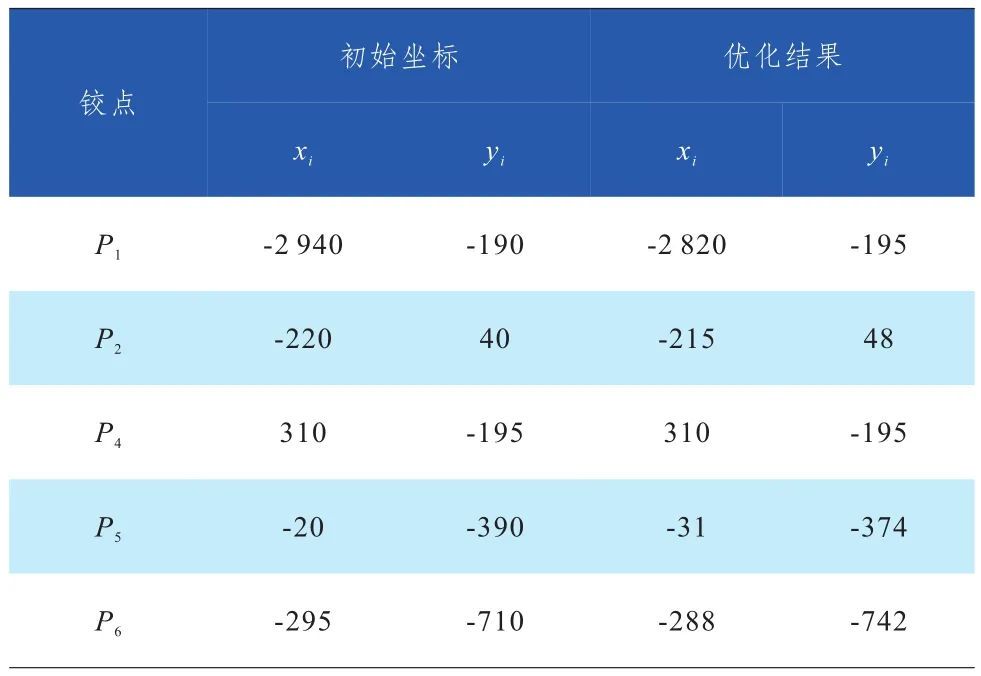
表1 初始坐标与优化结果 单位:mm
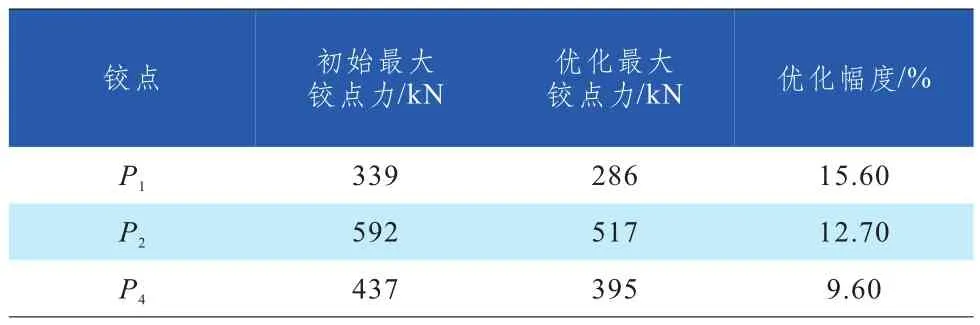
表2 初始最大铰点力与优化结果
优化前后各杆件的反力见图6。
5 分析与验证
5.1 有限元分析
臂架结构采用屈服强度为550 MPa的高强度结构钢,利用有限元分析软件对优化前后的曲臂变幅连杆机构进行结构强度分析,图7所示为曲臂水平、主臂75°时最大油缸支撑力状态下铰点优化前后的应力分布状况。
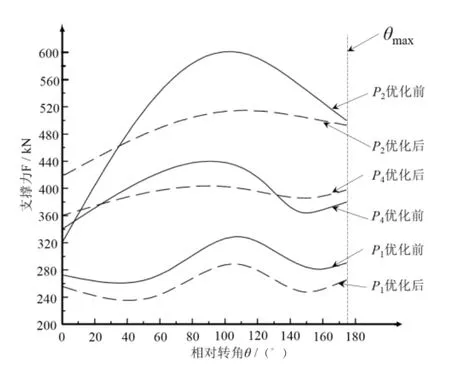
图6 铰点优化前后铰点反力图
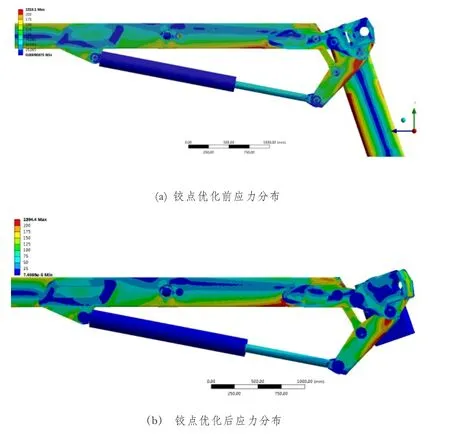
图7 曲臂变幅连杆机构应力分布
从优化前后连杆机构和曲臂的应力分布结果可以发现,在同样的负载下,优化后曲臂的局部应力虽有所增加,但大部分也都在200 MPa以内,而各铰点处的应力强度均有不同程度降低。优化的铰点分布,减小了铰点处的应力峰值,这证明了油缸支撑力相比优化前有所减小。
5.2 试验验证
为验证上述铰点优化和分析的正确性,对优化前后的曲臂连杆机构实物进行试验测量。曲臂水平、主臂75°、工作斗加载,使在铰点P3处的弯矩M为120 kN m,见图8。通过测量油缸无杆腔压力并计算得到油缸支撑力P1,沿连杆1的A点贴应变片,并计算得到铰点力P2。测量点布置见图9,测量并计算结果列入表3。
对比表2和表3的数值,铰点优化确实起到减小变幅油缸最大支撑力的作用,且理论与实测值误差小于7%,说明上述铰点优化和分析是正确的,准确性能满足工程实际应用的需要。

图8 应力测量试验
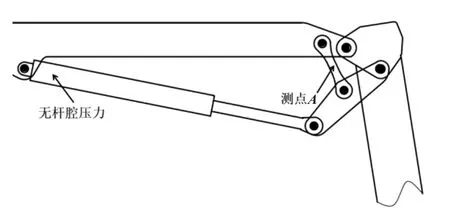
图9 部分测量点布置
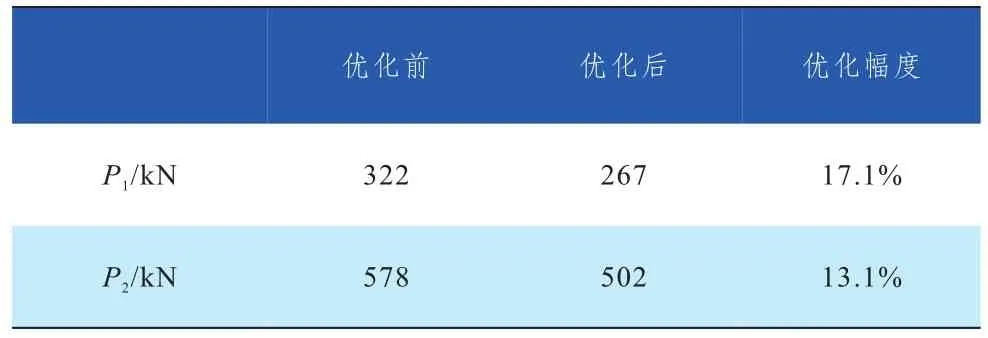
表3 部分试验测量并计算结果
得益于优化后变幅油缸最大支撑力的减小,变幅油缸的压杆稳定性将会得到增强。与此同时,在变幅油缸最大、支撑力减小的情况下,设计时也可以选用缸径规格较小的变幅油缸,这也有利于登高平台消防车的轻量化设计。
6 结语
本文建立了登高平台消防车曲臂变幅连杆机构的数学模型,并采用遗传算法进行了优化求解,后通过有限元强度分析和试验验证,得出以下结论:
a. 相比优化前,降低了变幅油缸出现最大支撑力时候的极值,油缸最大推力减小了15.6%;
b. 优化后的变幅连杆机构,除曲臂局部应力值稍有所增加,各连杆铰点处的反力降低;
c. 该方法可以大幅提高登高平台消防车臂架连杆铰点优化效率,从而缩短产品的研发周期。
