基于机器学习算法的电子音乐信号辨识模型
2021-01-28杨文华
杨文华
(渭南职业技术学院 师范学院, 陕西 渭南 714026)
0 引言
随着计算机技术的不断成熟,信号处理的能力得到提升,其在音乐生成领域得到了成功应用,产生了大量的电子音乐。由于大多数人都喜欢听音乐,但是电子音乐的种类繁多,每一个人喜欢的电子音乐类型不同,如果事先对电子音乐信号类型进行分类和辨识,听众可以从电子音乐信号标签中选择自己想听的电子音乐,这样能够大幅度提升电子音乐的管理水平,因此电子音乐信号的分类和辨识成为人工智能领域的一个重要研究方向[1-3]。
多年以来,人们对电子音乐信号辨识问题进行研究,电子音乐信号辨识包括多个因素[4],如风格、音量、音调、旋律、音色、和声等,是一个十分复杂的过程,与多种技术有关,如信号处理、人工智能、电子技术等,起初采用人工方式进行电子音乐信号辨识研究,它们根据自己对电子音乐信号的经验实现,因为存在太多的主观意识,不仅人工方式辨识效率低,而且电子音乐信号辨识误差比较大,不能满足现代电子音乐发展的速度[5-6]。随后出现了人工智能的电子音乐信号辨识方法,如线性判别分析的电子音乐信号辨识方法、人工神经网络的电子音乐信号辨识方法、支持向量机的电子音乐信号辨识方法,它们获得比人工方式更好的电子音乐信号辨识结果[7-9],但是在实际应用中,这些方法存在一定的不足:线性判别分析的电子音乐信号辨识正确率低,其认为特征向量和电子音乐信号类型之间是一种固定的线性变化关系,无法反映电子音乐信号的变化趋势;支持向量机的电子音乐信号辨识效率低;人工神经网络对噪声的干扰鲁棒性弱,因此电子音乐信号辨识有待进一步研究[10]。
为了提高音乐信号辨识正确率,提出了一种基于机器学习算法的电子音乐信号辨识方法,采用最小二乘支持向量机建立电子音乐信号辨识模型,并采用Matlab 2018编程实现电子音乐信号辨识的仿真实验,验证了本文电子音乐信号辨识方法的有效性和优越性。
1 机器学习算法的电子音乐信号辨识方法
1.1 机器学习算法的电子音乐信号辨识原理
机器学习算法的电子音乐信号辨识方法。首先对电子音乐信号进行采集,并引入去噪方法对其进行预处理,抑制噪声对音乐信号辨识的干扰,提高抗噪鲁棒性,然后从去噪后的电子音乐信号中提取能够描述其类型的特征向量,其与电子音乐信号类型组成学习样本,最后通过采用机器学习算法的最小二乘支持向量机对学习样本进行训练构建电子音乐信号辨识模型,如图1所示。

图1 电子音乐信号辨识原理
1.2 电子音乐信号的去噪处理
由于电子音乐信号的采集环境比较复杂,通常在室内,由于回波、信号折射、人员走动以及技术人员自身的水平等因素影响,得到的电子音乐信号含有一定的噪声,这样对电子音乐信号辨识结果会产生干扰,一个带有噪声的电子音乐信号y(n),如式(1)。
y(n)=x(n)+e(n)
(1)
式中,x(n)表示无噪声的电子音乐信信号;e(n)表示噪声。
采用小波包方法对电子音乐信号去噪,基本思想为:采用小波包对电子音乐信号进行分解,产生高频和低频两种电子音乐信号,对低频电子音乐信号进行进一步分解,不断分解下去,直到满足要求为止。电子音乐信号的正交尺度函数为φ(x),其小波函数为ψ(x),如式(2)、式(3)。
(2)
当μ0=φ(x),μ1=ψ(x),得到:
(3)
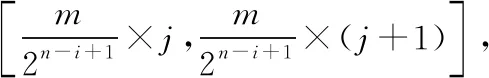
1.3 电子音乐信号特征向量的构建
不同的电子音乐信号,具有不同的特征向量,建立电子音乐信号辨识模型主要用于描述特征向量和电子音乐信号类型之间的映射关系。电子音乐信号特征主要包括3类:时域特征、频域特征和Mel 倒谱系数,因此本文提取这3类特征进行电子音乐信号辨识。
1.3.1 提取电子音乐信号的时域特征
电子音乐信号的时域特征很多,本文选择短时能量特征、短时平均过零率特征,对于电子音乐信号{x(n)},其短时能量的计算,如式(4)。
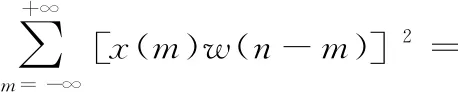
(4)
式中,h(n)=w2(n)表示电子音乐信号的单位冲击响应。
短时平均过零率的计算,如式(5)。
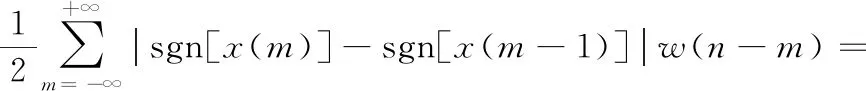
(5)
式中,sgn表示符号函数。
1.3.2 提取电子音乐信号的频域特征
电子音乐信号的频域特征选择谱质心、子带能量和带宽,先对电子音乐信号进行傅里叶变换,得到F(w),然后得到谱质心、子带能量和带宽的计算,如式(6)—式(8)。
(6)
(7)
(8)
式中,w0表示信号电子音乐采样频率的1/2;Hj和Lj分别表示傅里叶变换子带的上下边界频率。
1.3.3 提取电子音乐信号的Mel倒谱系数
Mel倒谱系数是一种关键电子音乐信号辨识特征,建立在傅里叶变换和倒谱分析基础上,电子音乐信号的每个子带宽度,如式(9)。
Mel(f)=2 595lg(1+f/700)
(9)
电子音乐信号的Mel倒谱系数特征提取步骤具体如下。
Step1:采用傅里叶变换对电子音乐信号进行处理,得到频谱X(k),如式(10)。
(10)
Step2:建立Mel倒谱的滤波器组,采用Mel滤波器组对X(k)进行处理,得到信号的功率谱Sk。
Step3:采用离散余弦逆变换计算Mel倒谱系数,如式(11)。
(11)
式中,K表示滤波器的数量。
1.4 机器学习算法的电子音乐信号辨识
最小二乘支持向量机是最近流行起来的一种机器学习算法,其学习速度要快于支持向量机,学习效果要优于人工神经网络,因此选择其建立电子音乐信号辨识模型。设电子音乐信号辨识特征和信号类型组成训练样本集合:{(xi,yi)},i=1,2,…n,xi∈Rn,yi∈R,xi和yi分别为电子音乐信号辨识特征和类型,如式(12)。
f(x)=wTφ(x)+b
(12)
对式(12)进行变换求解,如式(13)。
s.t.
yi-wTφ(x)+b=ei
(13)
式中,γ表示最小二乘支持向量机的参数。
由于式(13)的计算过程十分复杂,建立其等价形式,如式(14)。

(14)
根据最优化理论,如式(15)。

wTφ(xi)+b+ξi-yi=0
(15)
根据K(xi,xj)=φ(xi)Tφ(xj),得到最小二乘支持向量机的电子音乐信号辨识模型形式,如式(16)。
(16)
K(xi,xj)定义,如式(17)。
(17)
式中,σ为径向基宽度。
2 仿真实验
2.1 实验数据
选择Matlab 2018作为仿真实验的工具,并编写了电子音乐信号辨识程序。采用6种电子音乐信号仿真测试对象,它们分别是古典、迪斯科、流行音乐、摇滚、爵士、乡村,电子音乐信号辨识结果采用交叉验证进行。电子音乐信号的训练、验证样本的数量,如表1所示。
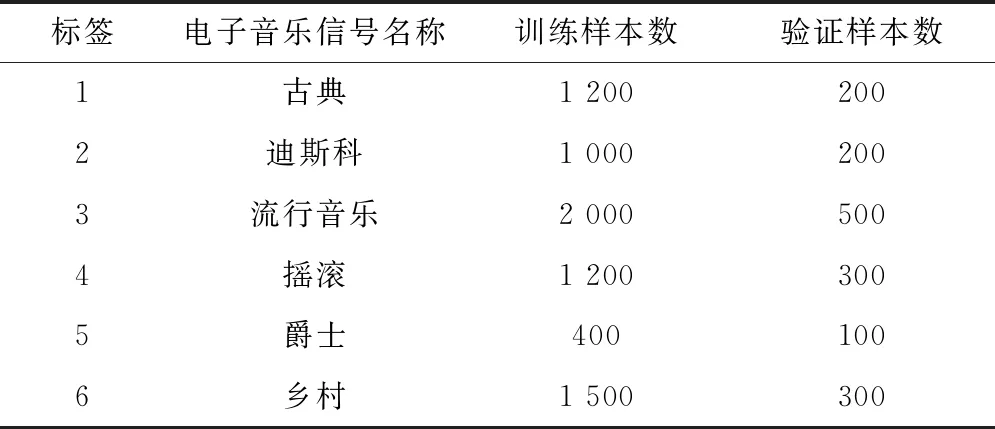
表1 电子音乐信号仿真实验的数据
2.2 与经典方法的电子音乐信号辨识性能对比
采用支持向量机、BP神经网络的电子音乐信号辨识方法作为对比方法,统计它们对6种类型的电子音乐信号验证样本集合辨识正确率,如图2所示。

图2 电子音乐信号辨识正确率
对图2的电子音乐信号验证样本集合辨识正确率进行对比和分析,可以得出结论:机器学习算法的电子音乐信号辨识正确率要高于支持向量机、BP神经网络的辨识正确率,减少了电子音乐信号辨识错误率,解决了当前电子音乐信号辨识结果不理想的问题,证明了本文方法的电子音乐信号辨识结果的优越性。
由于当前电子音乐数量不断增加,向大规模方向进行发展,为了适应现代电子音乐信号发展要求,电子音乐信号辨识的时间亦十分重要,统计3种方法对6类电子音乐信号辨识时间(秒,s),如表2所示。

表2 电子音乐信号辨识时间(s)
从表2可以看出,机器学习算法的电子音乐信号辨识时间要明显少于支持向量机、BP神经网络,加快了电子音乐信号辨识速度,在相同时间内,可以辨识更多的电子音乐信号。
3 总结
电子音乐信号的辨识具有重要的实际应用价值,成为人们的关注焦点,为了提高电子音乐信号的辨识正确率、减少电子音乐信号的辨识误差,提出机器学习算法的电子音乐信号辨识方法,在相同条件下,与经典方法进行了辨识仿真实验,机器学习算法的电子音乐信号辨识正确率远远高于实际应用的要求,信号辨识误差低于经典方法,为解决电子音乐信号辨识问题提供了一种新的研究思路。
