一种新型自复位SMA 支撑的抗震性能试验研究

2021-01-27胡淑军姜国青熊进刚

工程力学 2021年1期

胡淑军，顾琦，姜国青，熊进刚

(1. 南昌大学建筑工程学院，江西，南昌 330031；2. 江西省近零能耗建筑工程实验室，江西，南昌 330031；3. 洪都建设集团有限公司，江西，南昌 330029)

当前建筑结构的抗震性能和震后快速恢复能力被日益重视[1]。传统的结构抗震设计常采用增加结构自身延性来满足更强的地震要求，但震后可能引起结构过大的残余变形，导致结构震后修复困难[2]。可恢复功能结构能在提高结构抗震性能的同时，将损伤集中在可快速修复的耗能构件上[3]。带屈曲约束支撑[4]、偏心支撑[5]等的结构可有效提高其抗侧刚度和抗震性能，并将耗能和损伤集中在耗能构件上，且损伤构件震后也能被快速修复，但可能出现的残余变形会给整体结构的修复带来极大困难。因此，需在提高耗能支撑抗震性能的同时，有效减小构件残余变形并增强构件自复位能力。

形状记忆合金(SMA)是一种具有形状记忆效应、超弹性，在奥氏体相能表现出超弹性的材料，其恢复应变可达6%～8%[6]，且受温度[7]、加载速率[8]等因素影响。SMA 棒材和SMA 丝材均可用于土木工程中，SMA 棒材的承载能力高，但在应力较大时可能产生残余变形[9−10]，且性能不如SMA 丝材稳定[11]。SMA 丝材可用于自复位阻尼器中，并表现出良好性能[12−17]，例如：任文杰等[8]提出一种形状记忆合金-摩擦复合阻尼器，可根据不同输入荷载切换不同的工作机制；Dolce 等[12]利用SMA 分段受拉原理研制出一种SMA 自复位阻尼器，即构件在拉、压荷载下由不同的SMA 组提供自复位和耗能；Ozbulut 等[13]提出并研究一种基于SMA 和摩擦的耗能装置RVFD，并应用于高层建筑中；刘明明和李宏男等[14]提出一种自复位SMA-剪切型铅阻尼器，由SMA 丝材、剪切型铅块和复位弹簧组成；孙彤等[15]设计了一种新型多维SMA 阻尼器，能将扭转运动转化为阻尼缘拉伸，从而提供拉压及扭转方向阻尼；Feng 等[16]基于SMA 环提出一种非对称的自复位支撑，并用于钢结构梁柱节点中，有效避免节点损伤及提供自复位能力；展猛等[17]基于SMA 材料和压电PZT陶瓷驱动器，提出一种复位型SMA 压电混合减震装置。

高强螺杆在长圆孔中的摩擦滑移可增大构件延性和耗能能力，且板件间设置不同种类垫片的摩擦系数差异很大[18−19]。其中，采用1 mm 厚的丁基橡胶所制成的垫片，其摩擦系数可低至0.075[4]。另外，在支撑中合理设计两个长圆孔和滑移螺杆，并在螺杆之间设置SMA 丝材，可使其在拉力或压力作用下SMA 始终受拉[13]，从而进一步增大其耗能能力，并使其滞回曲线趋向旗帜型，降低构件的残余变形。

本文基于SMA 的自复位性能和滑移螺杆在长圆孔中的摩擦滑移耗能等思想，并结合丁基橡胶垫片的低摩擦效应，提出一种抗震性能良好和自复位能力强的新型自复位SMA 支撑，其中SMA始终受拉。设计五个不带SMA 的支撑和六个自复位SMA 支撑并进行低周往复加载试验研究，并仅考虑温度为20 ℃且加载速度为0.0012 s−1[20]，可得到支撑的滞回曲能、骨架曲线、割线刚度、耗能能力、承载能力和自复位能力等抗震性能指标，为该种新型自复位SMA 支撑的应用提供理论基础。

1 自复位SMA 支撑的基本性能

1.1 自复位SMA 支撑的构造

如图1 所示，自复位SMA 支撑的主要组成构件包括：前副板、后副板、左端板、右端板、高强螺栓、固定垫片、滑移螺杆、滑移垫片、丁基橡胶垫片、SMA。在前副板、后副板和右端板中间左、右两侧同一位置处分别开设长圆孔；在前副板、后副板和右端板上、下同一竖轴上分别开设螺栓圆孔。在两个长圆孔处的各板两侧分别设置丁基橡胶垫片，然后在丁基橡胶垫片远离各板一侧设置滑移垫片，并通过滑移螺杆将前副板、后副板和右端板固定连接，且滑移螺杆均设置在长圆孔内靠近另一长圆孔端部一侧，如图1(a)滑移螺杆位置。在螺栓圆孔处各板两侧分别设置固定垫片，并通过高强螺栓固定连接。当螺栓及螺杆均固定后，在两个滑移螺杆上分别缠绕SMA 丝材，即可形成新型自复位SMA 支撑。

1.2 自复位SMA 支撑的工作原理

自复位SMA 支撑初始状态如图2(a)所示。前副板、后副板和左端板受两个高强螺栓的固定作用，不发生任何滑移和变形。假设左端板在远离右端板一侧截面初始为固接，当右端板承受拉力作用时，右端板将带动右侧滑移螺杆向右侧移动，而左侧滑移螺杆受前副板和后副板内的左侧长圆孔固定，不发生滑移，故SMA 丝材将处于受拉状态，如图2(b)；当右端板恢复至初始状态且逐渐受压力作用时，右端板将带动左侧滑移螺杆向左侧移动，此时右侧滑移螺杆受前副板、后副板内的右侧长圆孔固定，也不发生滑移，SMA 丝材仍处于受拉状态，如图2(c)。此外，当外力卸载后，SMA 丝材的恢复力可为支撑提供复位力，且具有一定的耗能能力。在整个受力过程中，丁基橡胶垫片的设置将有效减小各板件与滑移垫片之间的摩擦力，增强构件的自复位能力。基于此，该种支撑在拉力、压力作用下SMA 始终受拉，有效实现构件的自复位能力。

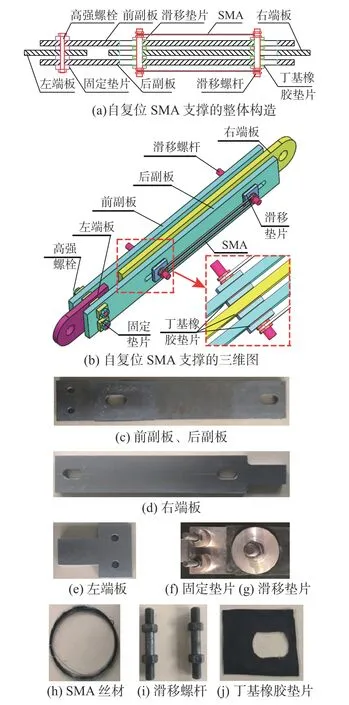
图 1 自复位SMA 支撑构造图Fig. 1 Schematic diagram of self-centering SMA brace

图 2 自复位SMA 支撑工作原理图Fig. 2 Work principle of self-centering SMA brace

1.3 自复位SMA 支撑的组装

单个自复位SMA 支撑部件包括：1 块左端板、1 块右端板、1 块前副板、1 块后副板、2 束SMA 丝材、8 块滑移垫块、8 块普通垫块、12 块丁基橡胶垫片、2 个高强螺栓、2 个滑移螺杆。各部件加工完成后，按如下步骤进行组装：

1)将裁剪好的丁基橡胶垫片粘贴在前副板、后副板、右端板与滑移垫块接触位置，如图3(a)；

图 3 自复位SMA 支撑的组装图Fig. 3 Assembly drawing of self-centering SMA brace

2)依照支撑构造图，采用滑移螺杆将滑移垫块、前副板、后副板、右端板固定连接，并将滑移螺杆安装在预定位置。随后采用高强螺栓将普通垫块、前副板、后副板和左端板固定连接。待上述装配完毕后，使用扭矩扳手对滑动螺杆的两侧螺母施加扭矩至目标值，如图3(b)；

3)由于SMA 丝材刚度较大，人工缠绕SMA丝材无法与滑移螺杆紧密贴合。设计一种方钢支撑套筒，其轴线距与支撑滑动螺杆的轴心距相同。将锚固好的SMA 丝材，通过套筒、圆形杆将预应力张拉到目标值，并采用方钢支撑卡住两套筒中间。另外，SMA 丝材之间采用鸡心形连接。具体如图3(c)；

4)取出设置了预拉力的SMA 丝材，并套入位于初始位置的滑移螺杆内，即可形成本文所提出的自复位SMA 支撑，如图3(d)。

2 试验概况

2.1 试件设计

为研究新型自复位SMA 支撑的抗震性能及自复位能力，设计多组考虑多种因素影响的模型，并对各构件进行试验研究。各主要参数如表1 所示。

表 1 试件主要参数Table 1 Table Main parameters of specimens

首先，设五个不带SMA 丝材的支撑模型(模型1～模型5)，以考虑滑动螺杆扭矩值的影响，并得到支撑承载力与扭矩值的关系。其次，设计六个带SMA 的模型，以考虑扭矩值、SMA 面积和SMA 预应力对支撑的影响。其中，两个模型的SMA 丝材横截面积分别是25.12 mm2、43.96 mm2(模型 6、模型 7)，分别是 16 圈 (两侧各 8 圈)、28 圈(两侧各14 圈)；两个模型考虑滑移螺杆扭矩值的影响(模型8、模型9)，并与模型7 对比；两个组模型考虑SMA 预拉力的影响(模型10、模型11)，并与模型7 对比。试件总长度为450 mm，最大位移行程为17 mm(约为SMA 长度的6%)。

在自复位支撑中，左端板尺寸为110 mm×80 mm×15 mm(长×宽×厚，下同)；前副板和后副板尺寸相等，均为424 mm×80 mm×8 mm；右端板长是424 mm×80 mm×15 mm；固定垫片半径为15 mm，厚5 mm；滑移垫片半径为40 mm，厚3 mm(两侧设置有1 mm 厚的丁基橡胶垫片)；螺栓圆孔半径为5 mm，长圆孔半径为10 mm，长度为17 mm，其它具体尺寸详见图4。

图 4 自复位SMA 支撑的几何尺寸图Fig. 4 Details of the self-centering SMA brace

2.2 材料性能

1) SMA 丝材的力学性能

本次试验中选用NITI 形状记忆合金丝材，其直径为1 mm，长度为37.5 mm，合金成分为56.00%(Ni 原子分数，下同)、43.59%Ti、0.04%C、0.05%Co、0.10%Cr、0.01%Cu、0.015%Fe、0.10%Si、0.095% 其它元素。试验温度为20 ℃，SMA 丝材的初始状态为奥氏体状态，且参照文献[20]加载速度取0.0012 s−1，且忽略其它加载速率的影响。采用SANS 电子万能试验机对SMA 丝材进行单一应变循环加载、逐级增量应变加载，具体表示为：

① 单一应变循环加载：对SMA 丝材进行幅值为 0.06 应变、加载速率为 0.0012 s−1的 30 圈循坏加载；

② 逐级增量应变加载：对SMA 丝材进行幅值为0.06 应变、增幅为0.01 应变/次、加载速率为 0.0012 s−1的循环加载。

如图5 所示SMA 丝材的应力-应变曲线。在单一应变循环加载中，当SMA 丝材在应变0.06下循环30 圈后，应力及应变均减小，最后回到初始状态，曲线呈明显的旗形，无明显残余变形，即SMA 丝材具有良好的自复位能力。另外，SMA丝材30 圈的循环拉伸曲线几乎保持重合，即力学曲线无明显改变和退化。在逐级增量应变加载中，其骨架曲线的轮廓与单一应变循环加载的曲线一致。当应变逐步增大时，曲线围成的图形为呈旗型，且每级应变下的应力、应变均能回归至初始零状态，其耗能能力也在逐渐增大。

图 5 SMA 丝材的应力-应变曲线Fig. 5 Stress-strain curve of SMA wire

图 6 SMA 的本构模型Fig. 6 Constitutive model of SMA

基于以上力学试验所得SMA 丝材的应力-应变曲线，可得到各参数的值，具体如表2 所示。

表 2 SMA 丝材的力学参数Table 2 Mechanical parameters of NITI-SMA wire

2)钢板的材料性能

自复位SMA 支撑中，各连接板件采用Q345B钢材，前副板、后副板厚度均为8 mm，右侧板厚度为15 mm。材性试验结果见表3。

表 3 钢板的力学参数Table 3 Mechanical properties for steel plate

2.3 试验装置及加载制度

本次试验在南昌大学工程力学实验室进行。如图7 所示，加载设备为SDS100 电液伺服试验机，且采用试验机中的静力试验模块，其最大加载力为100 kN，并采用液压夹头、液压驱动加载。安装时，采用夹头将左端板固定在下端，右端板也采用夹头固定在上端，并通过上端的力传感器同步施加和采集荷载和位移。整个试验过程中室温为20 ℃。

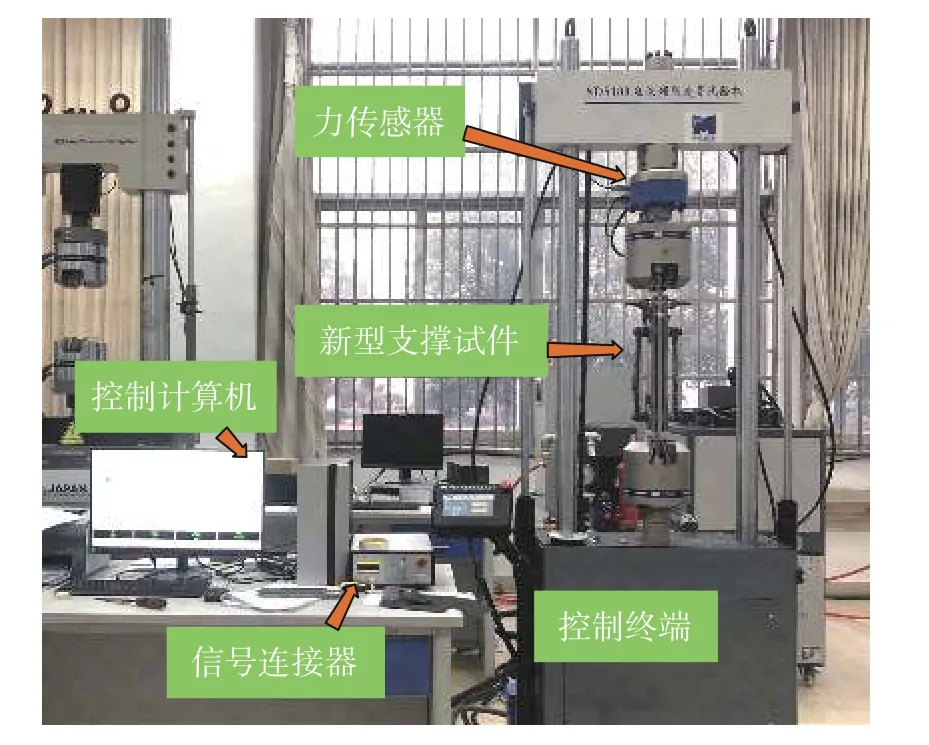
图 7 加载装置图Fig. 7 Experiment setup diagram

本文采用增量幅值加载的方式对构件施加位移荷载[8]，所采用的位移幅值和相应加载步如图8所示。加载速率为0.0012 s−1应变，换算成位移值为14.4 mm/min，如图8 所示。

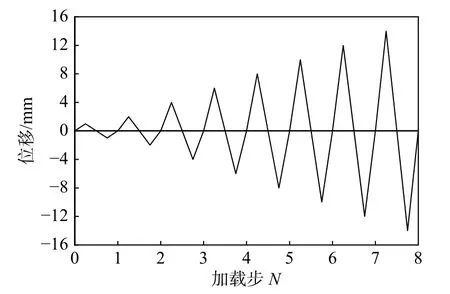
图 8 加载方式Fig. 8 Loading protocal

2.4 量测方案

各板件应变的测点布置方案如图9 所示。在右端板中部布置A1、A2、A3 应变片，间距为60 mm；在前副板、后副板中间布置A4、A5 应变片，以测量各板件在外力作用下的应力分布情况。此外，由于左端板、前副板、后副板在外荷载下不会发生移动，且加载时右端板的力和位移自动采集。构件的自复位率可通过滞回曲线中的残余变形和加载位移值进行确定，故整个加载过程中无需再布置位移计。

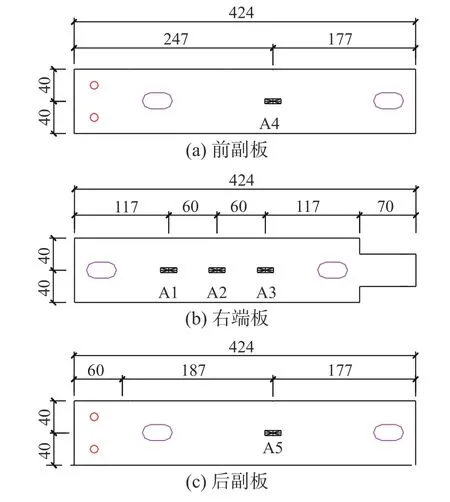
图 9 应变测点布置Fig. 9 Location of strain gauges

3 试验结果及分析

3.1 滞回曲线

1) 不带SMA 支撑的滞回曲线

当支撑的滑移螺杆间未设置SMA，且构件滑移距离小于长圆孔尺寸时，各板件的滑动需克服板件间丁基橡胶垫片所产生的摩擦力。此时，支撑的抗滑移承载力Fslip可表示为[19]：

式中：ns是摩擦面数目；nb是螺栓数目(等于2)；Tb是滑移螺杆预拉力；µ是抗滑移系数(取0.075[4])。

各构件的滑移螺杆在不同扭矩值下的滞回曲线如图10(a)所示。各构件在加载初期，轴向力较大，随后减小，这可能是由于相同压力下接触面之间的静摩擦力大于滑动摩擦力。当滑移进入稳定后，由于滑移螺杆间没有设置SMA，滑移螺杆移动至各加载位移时无法复位至初始状态，即滑移螺杆下次加载的初步位移值为上一步的加载位移值。另外，各加载步的初始加载时，仅有4 个摩擦面，随后增至6 个或8 个摩擦面，故各加载步后期轴力增大，且反向加载中进入4 个摩擦面的滑移。例如，第二个加载步后右侧滑移螺杆被拉至2 mm 处，在第三个加载步开始后，只有当位移加载到2 mm 时，右端板才接触到右侧滑移螺杆后摩擦面将明显增多，故轴力向会发生突变。因此，各构件滞回曲线中的轴力突变值主要由变化的摩擦面数目ns所引起的。此外，构件加载过后无法自复位，故其残余变形较大。

图 10 不带SMA 试件的滞回曲线Fig. 10 Hysteresis curves of specimens without SMA

取各支撑仅右端板在摩擦滑移且滑移螺杆未发生移动时(仅4 个摩擦面)的轴力值，并与相应扭矩值进行对比分析，如图10(b)所示。随着扭矩值的增大，构件轴力值也逐渐增大，大致呈线性关系，与式(1)理论计算值相符。分析结果可为自复位SMA 支撑的研究提供参考。

2) 自复位SMA 支撑的滞回曲线

图11 是考虑了SMA 面积、滑移螺杆预拉力和SMA 预应力的支撑滞回曲线，均明显的双旗型。另外，由于支撑在摩擦滑移时会产生抗滑移荷载，使得SMA 无法完全克服摩擦力并复位至初始状态，故会产生残余变形。各试件的主要变化趋势为：各加载步初期有一小段平滑段，随着位移和SMA 应力均增大，构件的承载能力也明显提高，整个往复加载过程中滞回曲线主要位于第一、第三象限，残余变形小，且复位效果明显。

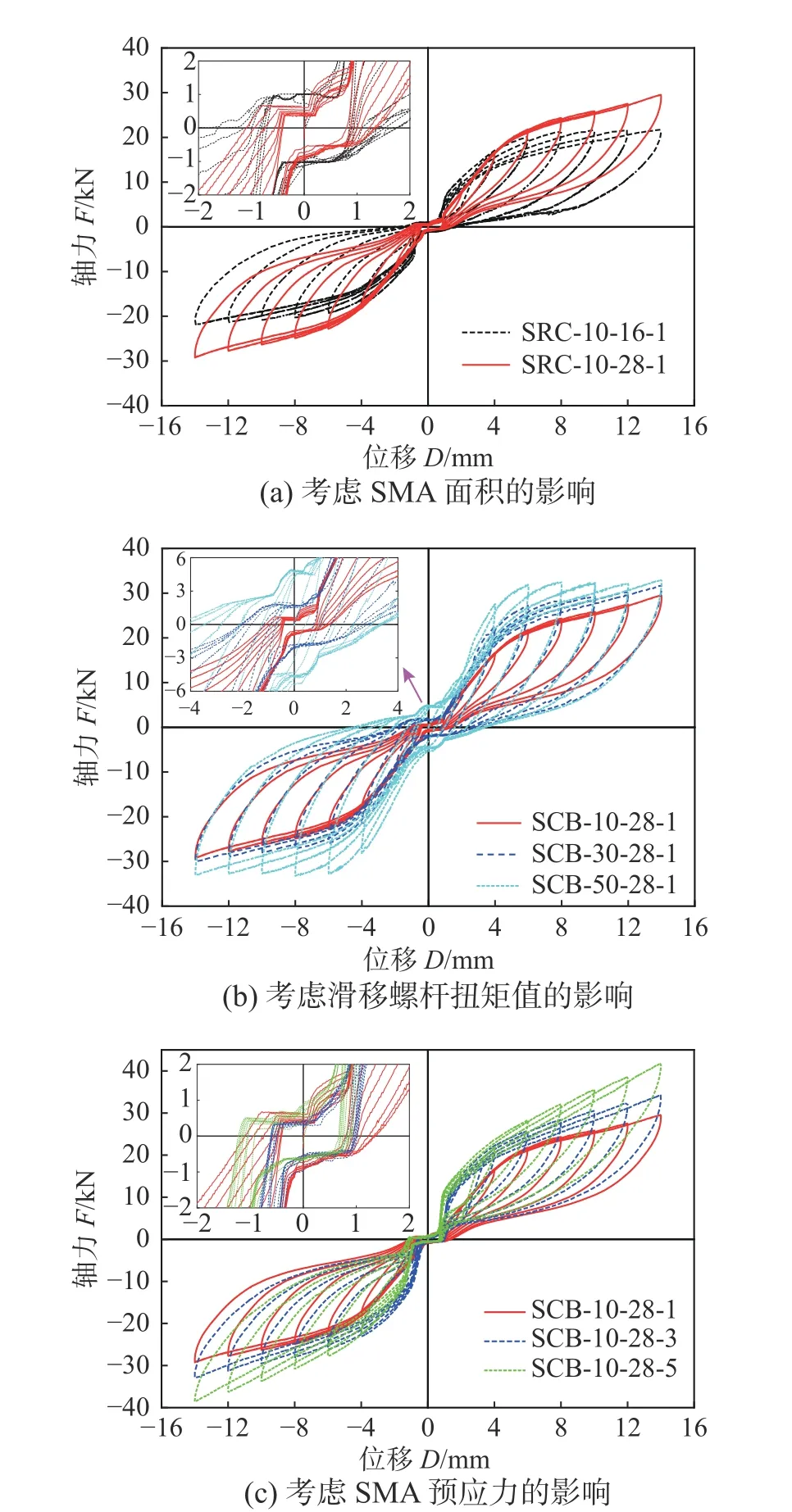
图 11 自复位SMA 支撑试件的滞回曲线Fig. 11 Hysteresis curves of self-centering SMA brace specimens

① SMA 面积的影响。如图11(a)，对比试件SCB-10-16-1 和 SCB-10-28-1 可知，增大 SMA 面积可有效提高构件的承载能力，并略微减小构件的残余变形。另外，增大SMA 面积对构件的抗滑移承载力无明显影响；

② 滑移螺杆扭矩力的影响。如图11(b)，对比三种试件的滞回曲线可知，增大滑移螺杆扭矩值可提高构件的承载能力，但该值的增量与构件抗滑移承载力的增量基本相同。同时，增大扭矩值还将使得构件的残余变形有所变大，影响其自复力能力；

③ SMA 预拉力的影响。如图11(c)，对比预拉力为1 kN、3 kN、5 kN 的曲线可知，增大SMA预拉力可提高构件的承载能力，但所得到的滞回曲线更捏缩，滞回面积更小，这主要是由于增大预拉力可使SMA 在相同位移下具有更高应力，但不会对抗滑移承载力和残余变形产生明显影响(预应力为5 kN 时的残余变形有所偏差，但正负残余变形基本相同，可能是由施工误差所致)，具有良好的复位能力。

3.2 骨架曲线

图12 给出了各自复位SMA 支撑的骨架曲线。从图中可以看出，各骨架曲线弹性阶段基本保持直线，随后呈上升趋并能达到预期位移，且各曲线关于原点对称。对比各构件骨架曲线可知，SMA 面积、螺杆预拉力和SMA 预拉力对构件的初始刚度和承载能力均有影响。

图 12 自复位SMA 支撑试件的骨架曲线Fig. 12 Skeleton curves of self-centering SMA brace specimens

3.3 割线刚度

自复位SMA 支撑的割线刚度可以反映其刚度退化的情况，可表达式为：

式中：Fmax、Fmin分别为第i 次循环加载时的最大正、负轴力；Dmax、Dmin分别为第i 次循环加载时的最大正、负位移。

图13 所示，各试件在正负两个方向上的割线刚度总体变化趋势相一致。加载初期，由于SMA应力较小，构件主要处于摩擦滑移，其割线刚度逐渐增大；随后SMA 应力增大，各构件割线刚度逐渐减小。当构件位移继续增大且SMA 应力缓慢上升时，刚度退化有所减缓并趋于相对稳定状态。此外，基于各构件的割线曲线可知，SMA 面积、螺杆预拉力和SMA 预拉力可提高构件的割线刚度。

图 13 割线刚度曲线Fig. 13 The curve of secant stiffness

3.4 应变变化规律

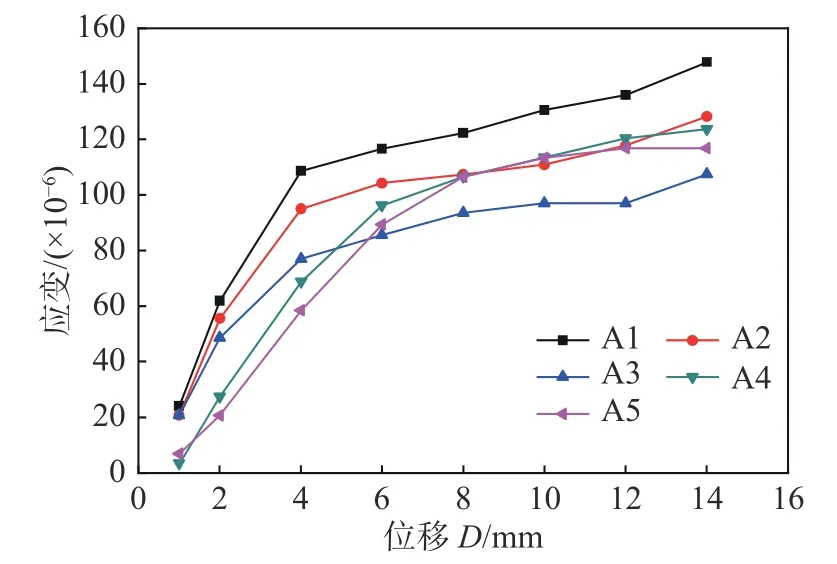
图 14 各监测点应变曲线Fig. 14 Strain curves of key positions

为研究自复位SMA 支撑在往复荷载下各板件的应变变化规律，取受力最大的SRC-10-28-5 试件为研究对象。根据表3 的材性数据可知，前副板和后副板的屈服应变为1772×10−6，右端板的屈服应变为1780×10−6。各监测点的最大应变值-位移曲线图14 如所示，各测点的应变值随位移的增大而增大，与承载力和骨架曲线变化趋势相同。测点A1、A2、A3 的应变变化规律基本一致，最大值分别为 145×10−6、128×10−6、107×10−6，即离左侧滑移螺杆近的应变值越大，但均远小于屈服应变；测点A4、A5 在加载步下的位移也基本一致，最大值为 126×10−6、122×10−6，小于屈服应变。此外，同一位移处的A2、A4、A5 最大应变值相近。

取A1 和A4 测点在往复荷载下的全过程应变-位移曲线对比，如图15 所示。根据图2 可知，试件受拉时，右端板仅右侧加载处至右侧滑移螺杆处受力，且前副板、后副板的受力处也仅为高强螺杆至左侧滑移螺杆之间，即此时测点A1、A4 均不会产生明显应力和变形；试件受压时，测点A1、A4 的受力变形与构件的受力变形相同。两测点在受压状态下的应变变化规律与试件的滞回曲线基本相同；受拉状态下的应变均较小，这与测点处的受力模式相同，同时也证明A1 应变值大于A4 应变值。

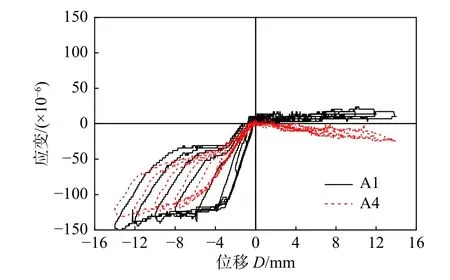
图 15 测点A1、A4 的应变-位移曲线Fig. 15 Strain-displacement curves of A1、A4 positions

3.5 耗能能力

为明确自复位SMA 支撑的耗能能力，研究各加载位移下试件耗能值的大小，如图16 所示。随着各试件位移的增大，相应耗能值也逐渐增加，即试件可提供稳定的耗能能力。对比试件SCB-10-16-1 和SCB-10-28-1 可知，在位移为14 mm 时的耗能值分别为206.1 J 和321.3 J，即增大SMA 面积可明显提高支撑的耗能能力；对比SCB-10-28-1、SCB-30-28-1 和 SCB-50-28-1 可知，最大加载步中的耗能值分别为321.3 J、407.8 J 和481.3 J，即增大滑移螺杆扭矩值也能有效增大支撑的耗能能力；对比 SCB-10-28-1、SCB-10-28-3 和 SCB-10-28-5 可知，最大耗能值分别为321.3 J、363.4 J和333.5 J，即小幅增加SMA 预拉力可有效改善支撑耗能能力，但预拉力值增加太多时，尽管可以提高构件的承载能力，同时滞回曲线也会带来较大捏缩现象，造成耗能值的下降，耗能变化规律需通过等效黏滞阻尼系数进一步判断。

图 16 试件耗能能力Fig. 16 Energy dissipation capacity of specimens

3.6 等效黏滞阻尼系数

图 17 试件等效黏滞阻尼系数Fig. 17 Energy dissipation indices of the specimens

3.7 承载力及自复位能力

对各自复位SMA 支撑试件的试验数据进行处理，可获得试件的最大承载力、抗滑移承载力、残余变形等参数。如图18 的自复位SMA 支撑在受拉状态下的力-位移曲线[21]可知，该种构件的承载力等于SMA 的承载力与滑移螺杆的抗滑移承载力两部分组成，且残余变形主要由旗帜形曲线与滑移曲线在卸载时所产生的。

图 18 自复位SMA 支撑的力-位移曲线Fig. 18 Force-displacement curve of self-centering SMA brace

结合图11 中各曲线值，可得如表4 的性能指标。增大SMA 面积、SMA 预应力对抗滑移承载力和残余变形无明显影响，但可以明显提高试件的最大承载力和自复位率，且最大自复位率达到93.7%。增大滑移螺杆扭矩值可增大构件的最大承载力，且抗滑移承载力与图10 中相应各扭矩值下的不带SMA 支撑结果基本相符，SMA 的承载力也基本保持不变，即承载力的增量仅为抗滑移承载力的增量，同时将明显增大支撑的残余变形，并降低其自复位能力。