水流作用下双圆柱墩混凝土梁桥的动力响应实测与数值模拟

华旭刚，邓武鹏，陈政清，唐 煜

(湖南大学风工程与桥梁工程湖南省重点实验室，湖南，长沙 410082)

西藏达林大桥是一座横跨雅鲁藏布江，跨径布置为35 m+5×30 m+35 m 的钢筋混凝土桥梁，下部结构采用双圆柱桥墩。2018 年7 月开通后不久，该桥在水流作用下桥墩及桥面出现了出乎意料的顺桥向大幅振动。水流流经桥墩会引起桥墩附近的冲刷，长期冲刷可能引起结构的安全性问题[1]。但本桥发生的是桥墩及桥面在横流向(顺桥向)的振动，是一种典型的流固耦合振动问题。刚度大、质量重的混凝土桥梁鲜有流致振动问题报道，为此本文开展了实测与数值模拟研究。

水流流经钝体断面时，断面两侧会出现边界层分离、旋涡产生及脱落等复杂的现象，并在断面上产生流体作用力，从而引起钝体断面或结构的流致振动问题，如顺流向的振动，横流向的涡激共振和驰振等。圆柱结构在桥梁、海洋立管、烟囱、输电线等很多工程领域均有应用，所以国内外学者对圆柱的绕流及流致振动问题进行了深入广泛的理论与试验研究，取得了大量的研究成果[2−5]。而桥墩一般为双圆柱结构，其上游柱会对下游柱的流场产生复杂的影响，且流动模式还与双圆柱的间距及来流与双圆柱中线的夹角等有关，因此其流固耦合问题更为复杂[6−8]。Zdravkovich[9]总结了串列双圆柱绕流中存在的六种流动模态，双圆柱振动响应的形式与这些流动模态存在紧密联系。Kim 等[10]进行了多个间距比下串列双圆柱的振动响应研究，分别讨论了三种自由度组合下的振动响应，证明了上游圆柱在一定间距比内对下游圆柱的振幅有增强作用。Zhou 和Alam[11]对现有双圆柱绕流及振动响应的研究进行了总结，并讨论了不同来流形式、雷诺数、流体力对双柱振动的影响；Zhao[12−13]对低雷诺数下刚性耦合双圆柱横流向振动进行了数值模拟，研究了串列和并列两种情况下的涡振响应。杜晓庆等[14]在高雷诺数Re=1.4×105下研究了串列双圆柱间距比与流场流态之间的关系，发现随着间距比的增大，双圆柱依次表现出单涡脱、剪切层再附和双涡脱三种流态。

还有部分学者针对桥墩绕流及墩水耦合作用进行了研究。刘晓亮等[15]对浅水下的大直径桥墩绕流进行了试验及数值模拟研究，发现靠近底部的小部分区域的漩涡脱落受到边界抑制，但整体上仍有规律的涡街出现，与二维模拟类似。杨万理等[16]对单圆柱桥墩绕流进行了三维数值模拟，分析了流体力沿水深的分布关系并探讨了自由液面及底部边界对流场的影响。Sun 和Liu[17]研究了深水桥墩结构动力响应，解释了水动压力对桥墩动力响应的影响。李乔等[18]对不同断面桥墩的墩水耦合振动问题进行了试验研究并通过CFD 软件验证了试验有效性，提出了用附加刚度法来模拟水中桥墩的弹性振动，发现桥墩底部的动水压力及自振频率会随水深的增大而增大，而各类地震波下的桥墩位移响应则会减小。曹宁宁[19]对不同横断面的桥墩进行了二维绕流数值分析，并利用ANSYS 计算了不同断面桥墩在不同入水深度和流速下的动力响应。张家瑞等[20]基于贝叶斯理论建立了波浪作用下深水桥墩的动力响应概率模型，修正了传统方法预测的偏差。

上述研究多是基于缩尺模型或数值模拟完成的，而对于实际桥梁、桥墩的流致振动响应及振动原因却鲜有深入研究。本文为进一步分析西藏达林大桥的振动原因，在雅鲁藏布江汛期时对该桥加速度及梁端位移进行了实测研究，并将桥梁简化成顺桥向振动的单自由度系统，通过Fluent对双圆柱式桥墩进行了绕流及流固耦合模拟。探讨了大桥顺桥向大幅振动的原因及桥墩入水深度、三维效应及结构阻尼比等对数值模拟结果的影响。

1 工程背景

达林大桥位于西藏自治区林芝市米林县派镇隆白地区，为跨径布置为35 m+5×30 m+35 m 的7 跨桥面连续的混凝土梁桥，全长220 m，如图1所示。大桥主梁全宽为8.5 m，由4 片小T 梁组成，通过板式橡胶支座支承于盖梁之上。桥墩采用双圆柱形式，双圆柱之间采用横梁连接。本桥于2016 年完工，2018 年7 月交工开通。开通不久后本桥伸缩缝处出现了显著的顺桥向振动，为探明振动原因，对达林大桥进行了动力测试。测试时正值雅鲁藏布江汛期，水位约处于桥墩上横梁位置，桥墩入水深度约为6.5 m。

图 1 达林大桥Fig. 1 The Dalin bridge

利用ANSYS 对大桥进行了有限元建模分析。由于特殊原因缺少部分设计图纸，无法直接得到桥梁所有构造及尺寸，故采用图像识别软件对现场拍摄照片进行尺寸识别。已知桥墩直径为1.3 m，得到构件尺寸识别结果如图2 所示。

由图2 可基本确定桥梁尺寸、截面与材料参数。经尺寸比对发现，本桥的主梁横截面及跨径、构造等均与《公路桥涵通用图》中编号为11-7的公路-II 级预应力混凝土简支T 梁近似，跨径30 m，桥宽8.5 m，标准断面见图3 所示，图3 尺寸单位均为mm。由图2、图3 中关于达林大桥的桥梁尺寸、截面以及材料参数，通过这些信息便可建立全桥ANSYS 有限元模型：主梁、桥墩、盖梁均采用BEAM188 模拟，主梁桥面连续，桥墩底部固结。本桥的一阶顺桥向和横桥向固有频率及等效质量如表1 所示。

图 2 构造尺寸确定Fig. 2 Determination of construction dimension

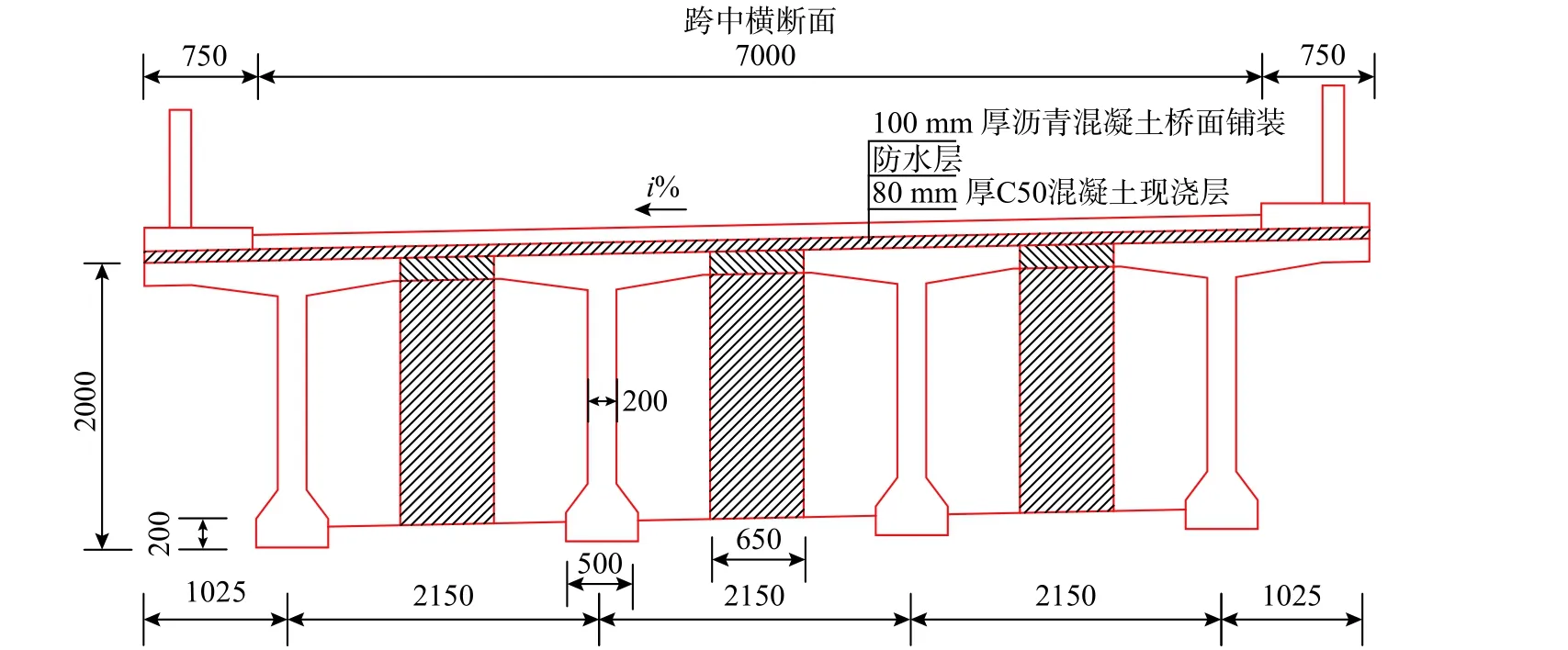
图 3 公路-II 级预应力混凝土简支T 梁截面 /mmFig. 3 Highway class II T-beam section

表 1 大桥固有模态Table 1 Natural mode of bridge

2 大桥振动实测

2.1 传感器布置与测试内容

在汛期对大桥进行了水流作用下的振动响应测试，测试时水流流速约为4 m/s。测试仪器包括加速度传感器及激光位移传感器。加速度传感器型号为东华公司的2D001 磁电式加速度传感器，灵敏度为0.3 V/(m/s)，量程为20 m/s2，采样频率为200 Hz。激光位移传感器采用的是KEYENCE公司的IL-300 号CMOS 激光位移计，量程为160 mm～450 mm，重复精度为30 µm，采样频率为200 Hz。由于现场条件限制无法将加速度传感器安装到桥墩顶部，各传感器均安装于桥面，激光位移传感器则安装在第一跨梁端伸缩缝处。图4 给出了各传感器的布置图。

现场测试获取了水流作用下大桥第一跨和第二跨在顺桥向(横流向)、横桥向(顺流向)、竖向三个方向的加速度响应及伸缩缝处的梁端相对位移响应，并识别出了各个方向的振动频率和阻尼比。

图 4 传感器布置图Fig. 4 Layout of sensors

2.2 测试数据分析

图5 和图6 分别为第一跨和第二跨顺桥向加速度时程及功率谱曲线，图7 为梁端位移时程与功率谱曲线。图8 是从实桥振动实况录像中取出的两个画面，分别对应伸缩缝处顺桥向振动的波峰与波谷状态，可发现顺桥向振动十分明显。图9和图10 分别为第一跨横桥向和竖向加速度时程及功率谱曲线。

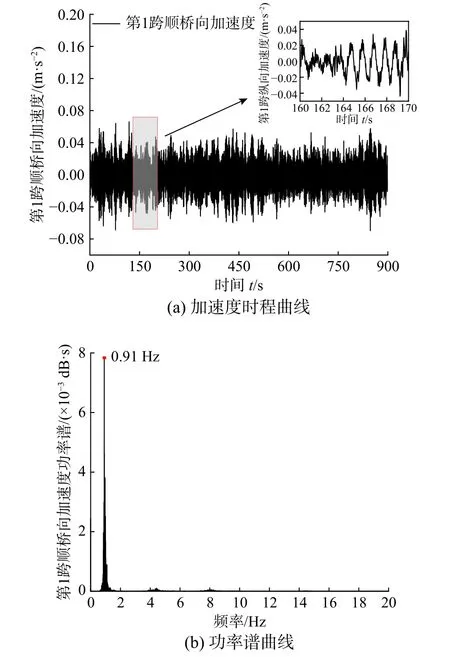
图 5 第一跨顺桥向加速度时程与功率谱曲线(传感器编号：4C)Fig. 5 Longitudinal acceleration of the first span and its power spectrum (sensor number: 4C)

图 6 第二跨顺桥向加速度时程与功率谱曲线(传感器编号：1C)Fig. 6 Longitudinal acceleration of the second span and its power spectrum (sensor number: 1C)

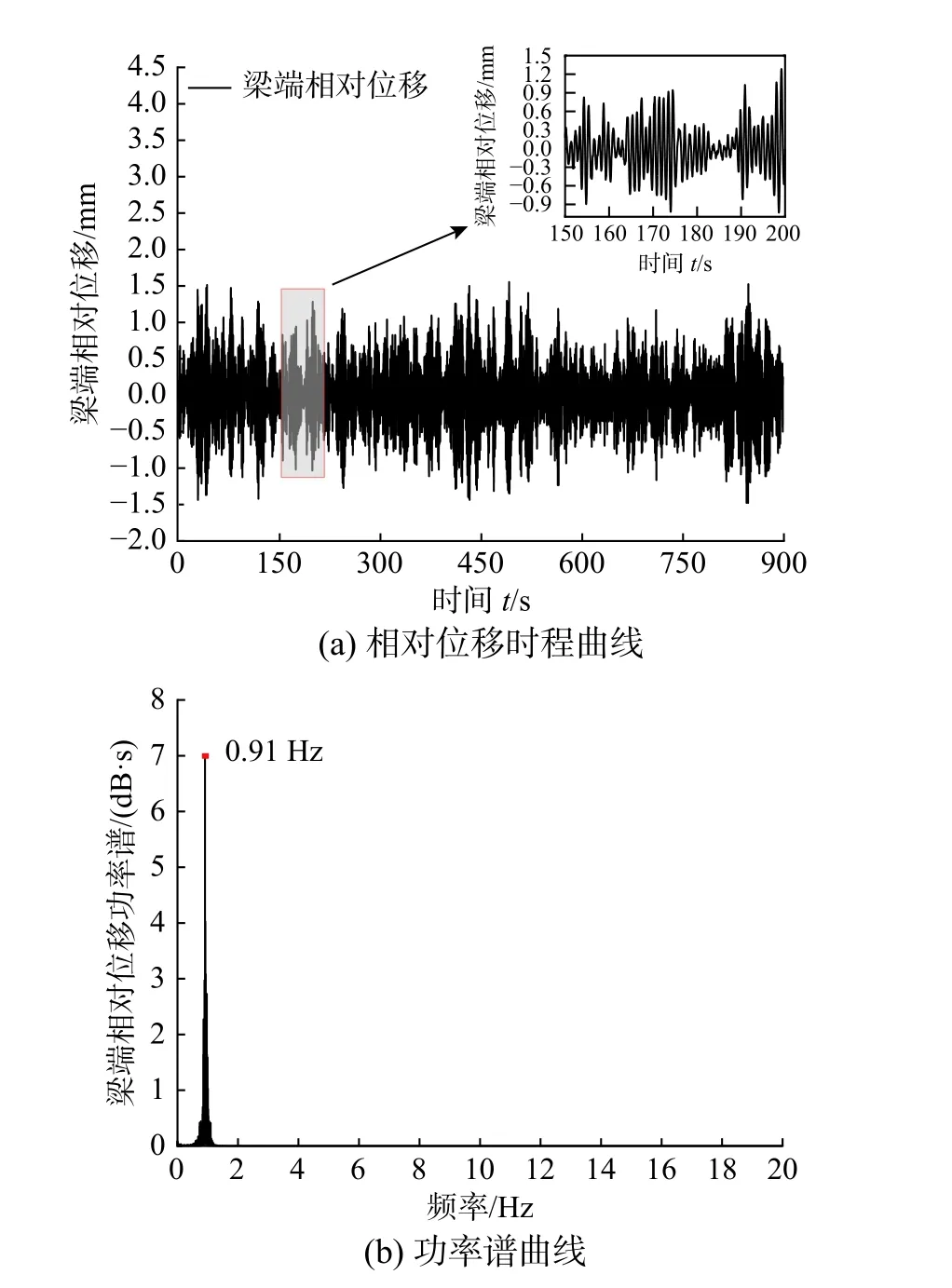
图 7 顺桥向相对位移时程与功率谱曲线(传感器编号：7C)Fig. 7 Longitudinal relative displacement of the bridge and its power spectrum (sensor number: 7C)

图 8 顺桥向振动实况图Fig. 8 Graphical illustration of longitudinal displacement of the bridge

由图5～图7 可知，4C、1C、7C 传感器识别出的顺桥向振动频率都为0.91 Hz，ANSYS 计算所得的大桥一阶顺桥向自振频率为0.94 Hz，两者之间误差为3.2%，可证明实测数据的准确性。由图9 可知，现场实测的横桥向振动频率为1.22 Hz和1.53 Hz，其中1.22 Hz 与ANSYS 计算结果1.24 Hz相接近。大桥横桥向和竖向振动的频率成分复杂，包含多个频率且加速度响应较弱，振动形式为随机微振动。

图 9 第一跨横桥向加速度时程与功率谱曲线(传感器编号：5C)Fig. 9 Transverse acceleration of the first span and its power spectrum (sensor number: 5C)

图 10 第一跨竖向加速度时程与功率谱曲线(传感器编号：6C)Fig. 10 Vertical acceleration of the first span and its power spectrum (sensor number: 6C)

观察顺桥向振动各时程数据可知，大桥顺桥向振动最大加速度约为0.08 m/s2，最大梁端位移为1.56 mm。顺桥向振动响应特别是梁端相对位移时程呈现“拍”的特点，类简谐形式；拍振现象可能是由于顺桥向上的水流激励频率即水流涡脱频率与桥梁自振频率接近所导致，初步判定在4 m/s左右的流速范围内，涡脱频率可能被顺桥向自振频率捕获，从而引起桥梁结构发生横流向的涡振。本文第4 节将利用流体分析软件Fluent 对墩顶位移随来流速度变化的响应进行研究，探讨振动原因。

为了后续研究，采用随机子空间法(SSI)对上述实测数据进行了阻尼比识别。随机子空间(SSI)是基于线性系统离散状态空间方程的识别方法，SSI 识别具有较高的准确性与较强的抗干扰能力[21]。本文主要关注桥梁在顺桥向上的振动，基于实测数据得到的顺桥向模态振动阻尼比范围为0.3%～3%，识别结果较为离散。故在CFD 仿真分析时设置ζ=0.01、0.02、0.03 三个不同阻尼比工况。

3 CFD 仿真分析

3.1 基本理论

作为一座桥面连续的多跨混凝土梁桥，达林大桥的桥墩是直接承受流体力的主要构件，是产生流固耦合作用的来源。为此，利用Fluent 对大桥双圆柱桥墩的绕流及流固耦合进行了二维断面的模拟与分析。桥墩模型布置示意图如图11 所示，圆心距T/D=3.7，x 轴为阻力方向即沿河道的顺流方向，y 轴为升力方向即垂直河道的横流方向。

图 11 桥墩模型布置图Fig. 11 Layout of twin cylinders pier

对于运动着的粘性不可压缩流体，其内的流体质点在外力作用下，运动参数将会以一定形式发生变化，考虑到运动着的流体质点必遵循动量守恒定律，即可得到运动参数间的特定关系，其数学表达形式即为N-S 方程，本文研究忽略了流体重力的作用，则N-S 方程可写为：

式中： yc(t)为墩顶位移响应；yf(t)为Fluent 计算所得位移响应。

3.2 计算模型及网格无关性检验

图12 为计算域及边界条件示意。结合湍流理论与动网格变形需求对计算域尺寸进行选择，以保证完整的流体绕流效应以及动网格变形需要。双圆柱直径D=1.3 m，为桥墩实际直径，圆心距T/D=3.7。计算域为方形，尺寸为100D×100D，可分为两部分：第一部分是加密的随桥墩一起运动的刚性区域；第二部分是自由变形动网格区域。计算域左边界为进口，定义为速度入口；右边界为出口，定义为压力出口；上下边界为对称边界。圆柱采用无滑移壁面边界条件，表面速度为零。本次计算流动为非定常，采用SIMPLEC 算法，空间离散采用Second Order Upwind 二阶迎风格式。

图 12 计算域及边界条件Fig. 12 Computational domain and boundary conditions

为检验网格无关性，保持其余参数不变，在来流流速U=4 m/s、雷诺数Re=3.9×106的条件下比较了周向网格数、径向网格数对计算结果的影响。表2 给出了Case 1～Case 4 等四种网格方案。图13 给出了Case 3 的网格方案图，图中圆柱周向共260 个单元，径向150 个单元，最小单元高度为 5×10−5。

表 2 网格参数表Table 2 Mesh parameter

图 13 Fluent 网格示意图Fig. 13 Fluent computational gird

表 3 不同网格数量的升、阻力系数对比Table 3 Comparison of lift and drag coefficients ofdifferent mesh numbers

3.3 双圆柱墩升阻力特性

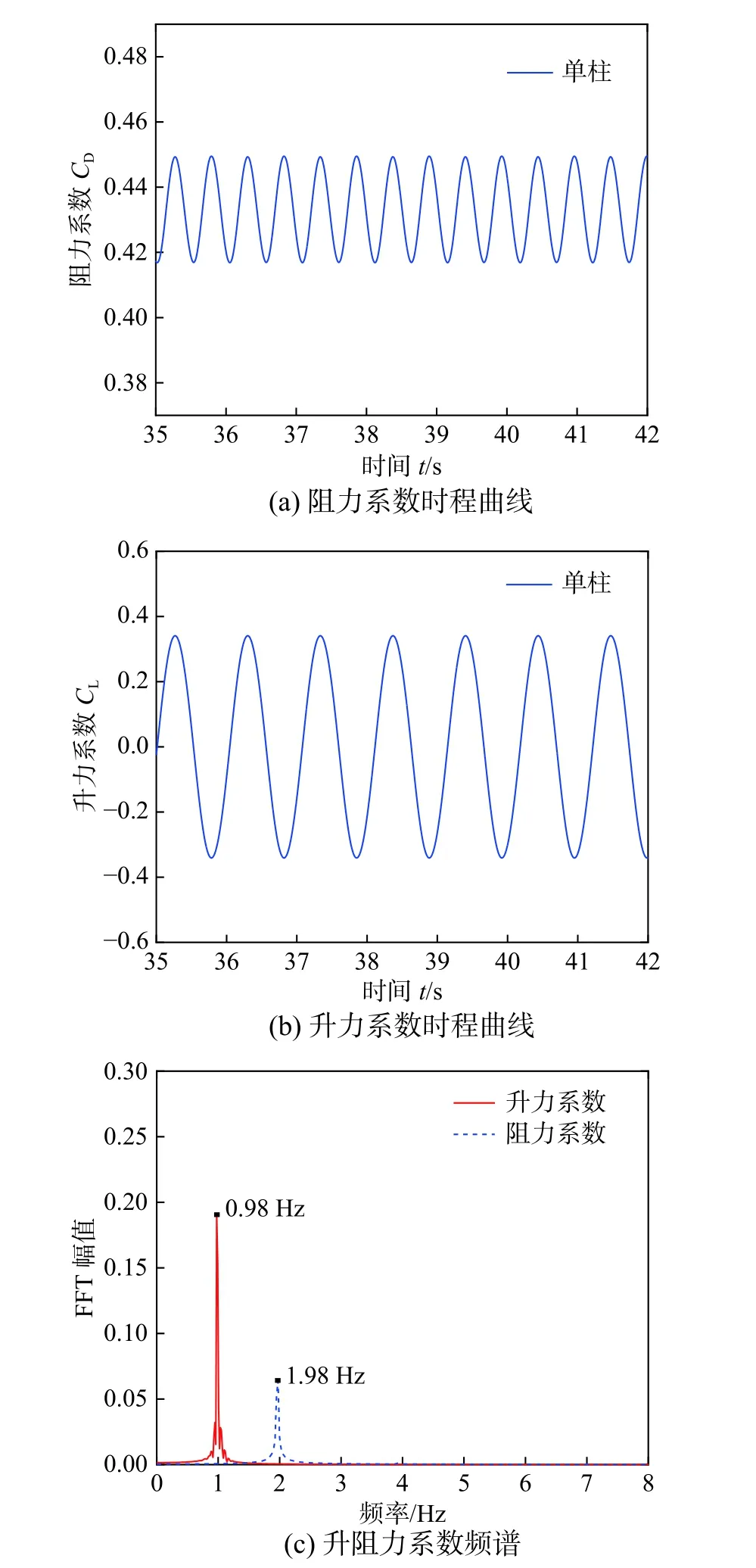
图 14 单圆柱升阻力系数时程及频谱(U=4 m/s)Fig. 14 Lift and drag coefficients of single cylinder and their frequency spectrum (U=4 m/s)

从图14 和图15 可发现，桥墩整体阻力系数频率为1.70 Hz，与现场实测的横桥向振动特征频率中的1.53 Hz 接近，说明1.53 Hz 为测试时的横桥向的流体力(阻力)频率，而1.22 Hz 为横桥向自振频率。桥墩整体升力频率为0.86 Hz 且上下游柱升力频率基本一致，略低于单圆柱升力频率；桥墩整体升力频率与现场实测的顺桥向振动特征频率0.91 Hz 相接近，再次说明了在接近4 m/s 的流速范围内，桥墩可能出现横流向的涡激共振。

3.4 二维振动响应

本节进行了流固耦合计算以研究位移与来流速度的关系。相关参数设置如下：来流流速U=2 m/s～10 m/s，雷诺数Re=2.6×106～1.3×107；质量比m*=4m/ρπD2=503.7，m 取 ANSYS 计算所得全桥顺桥向振动等效质量的1/6；自振频率f0=0.91 Hz；考虑到通过实测数据所识别出的阻尼比范围较广且可能存在水流的阻尼贡献，不能真实反映结构自身的阻尼特性，所以设置三个阻尼比工况，分别取ζ=0.01、0.02、0.03。

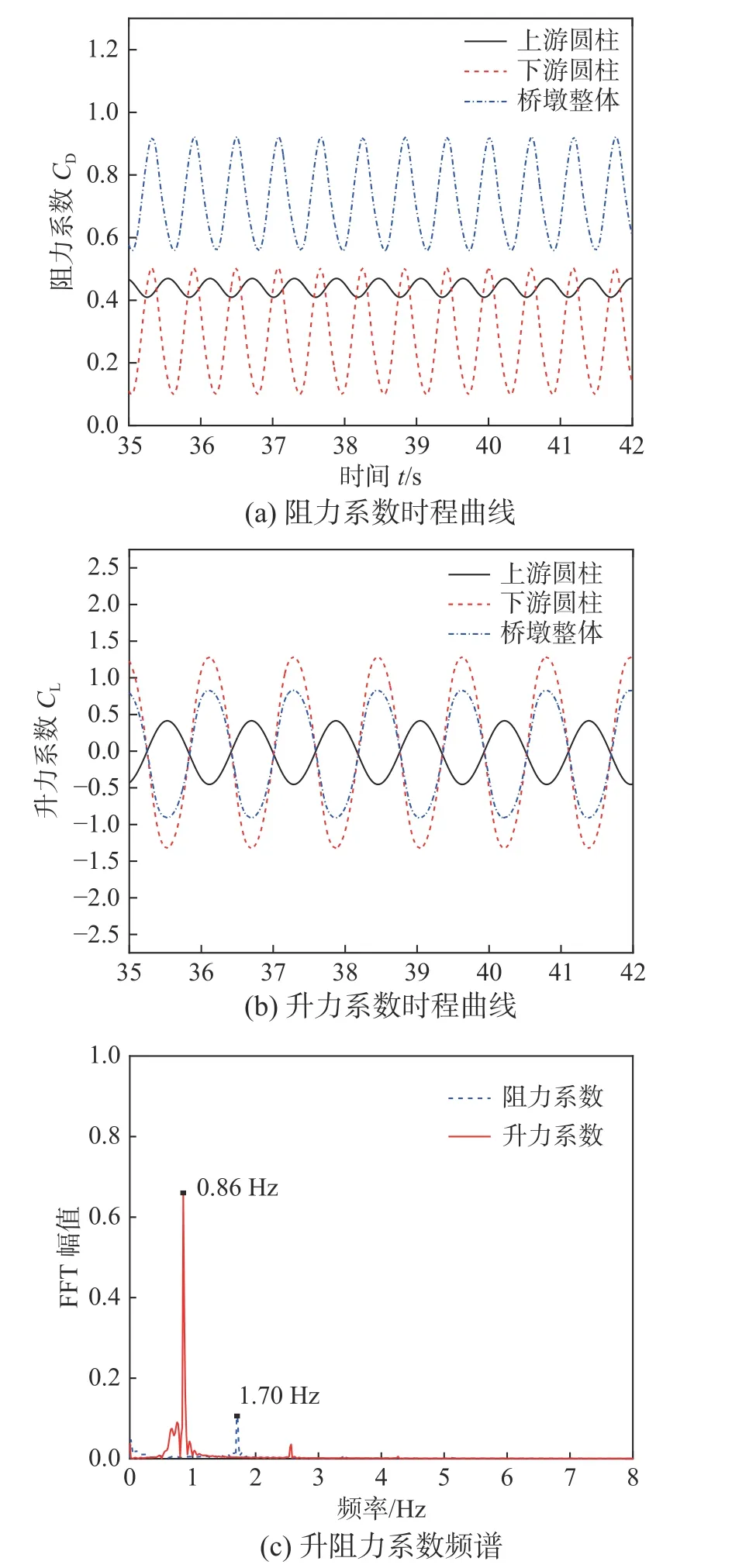
图 15 桥墩升阻力系数时程及频谱(U=4 m/s)Fig. 15 Lift and drag coefficients of twin cylinders and their frequency spectrum (U=4 m/s)

图16 给出了ζ=0.01 时，三个特定流速下的桥墩位移响应的计算结果。当U=2.5 m/s 时，ymax=0.33 mm，此时振幅很小；振动频率f =0.52 Hz，振动频率也远小于自振频率f0。当U=4.3 m/s 时，ymax=8.87 mm，振幅较大；振动频率f =0.93 Hz，大致等于f0。当U=8.0 m/s 时，振动频率f =1.86 Hz，ymax=1.90 mm，振幅下降且振动频率较高，此时桥墩在水流作用下做强迫运动。从图看出，由于忽略了振型及流速的三维修正，得到涡振振动幅要远大于实测值。限于篇幅，其他阻尼比的结算结果不作详细讨论，详见4.5 节。

3.5 墩顶位移动力响应

图 16 U=2.5 m/s、4.3 m/s、8.0 m/s 三种流速下双圆柱的位移时程曲线及频谱(ζ=0.01)Fig. 16 Displacement time history and its frequency spectrum of twin-circular cylinder at U=2.5 m/s、 4.3 m/s、8.0 m/s (ζ=0.01)

4.4 节得到的是二维双圆柱墩的动力响应，它没有考虑实际桥墩的振型效应及水流流速分布。利用式(7)对上述三种阻尼比时各个流速下的Fluent 计算所得位移响应yf(t)进行修正，即可得到各阻尼比下墩顶位移随来流流速变化的关系。图17 用经修正后的稳态振幅ymax对墩顶位移响应进行了描述：三个工况下的墩顶位移响应从U=3 m/s 开始急速增加，并均在U=4.3 m/s 达到最大值 ， 分 别 为 2.40 mm(ζ=0.01)、 2.18 mm(ζ=0.02)、1.80 mm(ζ=0.03)，此后响应开始急速下降，直到U≥6 m/s 后下降速度变缓。从响应随流速变化的情况可知，桥墩在3 m/s～6 m/s 的流速范围内发生了明显的涡激振动；阻尼比对墩顶位移的影响主要体现在涡振锁定区间内，随着阻尼比的增大，位移响应降低。

图 17 不同阻尼比下墩顶振幅随流速变化响应曲线Fig. 17 Variation of vibration amplitude of twin-pier top with velocity under different damping ratio

同时还可发现，当来流流速U=4 m/s，不同阻尼比 ζ 下 ymax分别为：1.60 mm(ζ=0.01)、1.24 mm(ζ=0.02)、1.13 mm(ζ=0.03)。实测的位移最大值为1.56 mm，与其进行比对可知，阻尼比ζ=0.01 时的位移与实测值最为吻合。

4 结论

本文针对达林大桥在水流作用下桥墩及桥面出现的顺桥向大幅振动这一情况，对其进行了现场实测及CFD 仿真分析的研究。现场实测表明，在流速约为4 m/s 的水流作用下，大桥顺桥向振动表现为桥梁一阶顺桥向模态为主的拍振。说明在4 m/s 左右的某个流速范围内水流涡脱频率可能被顺桥向自振频率捕获，从而导致涡振的发生。

随后将桥墩-桥面系统简化为顺桥向振动的广义单自由度体系，在流速U 为2 m/s～10 m/s 范围内 (Ur=1.69～8.45、Re=2.6×106～1.3×107)利用 Fluent进行了二维数值模拟。计算得到了4 m/s 下桥墩的升阻力系数，表明桥墩的上游柱对下游圆柱的脉动升力有增强作用。考虑桥墩振型与桥墩入水深度等三维效应，对Fluent 计算所得响应进行修正，得到了不同阻尼比下墩顶位移响应随流速变化的关系：在3 m/s～6 m/s 流速范围内均观测到了桥墩的涡激振动，解释了达林大桥桥墩及桥面在顺桥向上发生大幅振动的原因。桥墩发生涡振时，振动频率与顺桥向一阶自振频率接近，且发现随着阻尼比的增加，涡振最大振幅变小，锁定区间基本不随阻尼比发生改变。

在考虑三维修正后，ζ=0.01 工况下墩顶位移数值模拟结果与实测值较为吻合。后续应考虑不同流速下的桥墩入水深度、真实的来流流速分布等因素的影响以及三维CFD 分析，进而深入研究涡振振幅预测。