圆弧-线段一阶混合曲线及其插补算法*

马虎亮，吕 明，杨胜强，王燕青

(太原理工大学机械与运载工程学院，太原 030024)

0 引言

数控加工系统中主要以线段和圆弧为主，复杂图形的加工有两种办法，一种是在误差范围内，以多个微小线段和圆弧对曲线进行拟合；第二种是针对B样条曲线、NURBS曲线直接插补方法。第一种方法简单，插补算法较多，但得到的加工数据量大，不易存储和执行。第二种方法拟合过程复杂，但得到的曲线对象少。在计算结果方面，线段拟合段数最多，圆弧拟合段数次之，曲线拟合最少。因此，当前数控系统的研究热点之一便是曲线的拟合和插补方法。

B样条曲线和NURBS曲线引入与坐标系无关的参数，同时引入控制点，得到控制多边形，通过控制点和权因子等形状控制参数用多项式对目标曲线进行生成和拟合。同时由于很多设计软件中已经配置了曲线设计功能，在这种情况下，可以直接得到曲线的控制点信息，省去拟合的过程。NURBS已成为当前曲线曲面设计和拟合的标准形式。很多学者也对于NURBS 样条曲线的插补算法进行了研究[1-3]，对NURBS样条曲线曲面加工技术也进行了很多研究[4-5]。

NURBS样条曲线曲面具有很多优点：局部可调性、几何不变形和仿射不变性等，还可以精确地表示某些圆锥曲线段，但仍然具有一些缺陷[6-8]：①NURBS曲线曲面求导非常麻烦，次数太高，反复求导则其高阶导矢曲线的阶数快速上升；②变量较多，需要设计人员具有一定的数学基础；③不能完整的表示整段圆弧、摆线和螺旋线等曲线。 因此研究者们引入了包含三角函数和双曲三角函数的混合曲面曲线[9-10]，来表示更高要求的曲面曲线。

圆弧-线段一阶混合曲线包含三角函数，用样条曲线等有理函数拟合，必然存在误差和拟合精度等问题。由于其表达式可分解为线段和圆弧的表达式之和，因此提出了将线段和圆弧插补有机组合的插补合成法。

本文对圆弧-线段一阶混合曲线的特征进行分析并推导其参数表达式，然后说明插补合成法的原理和方法，最后对插补方法进行了验证。

1 圆弧-线段一阶混合曲线

圆弧-线段一阶混合曲线是指由圆弧和线段混合而成的曲线，其表达式中包含一阶多项式和一阶三角函数。线段与圆弧的混合包含线段与线段的混合、线段和圆弧的混合、两条圆弧的混合。几何元素在坐标系中的表达式通常有显示方程和隐式方程。线段和圆弧的一般显示方程和隐式方程如表1中所示。线段和圆弧插补算法一般基于表1中的表达式来推导。

表1 线段和圆弧的函数表达式

表中可以看出，圆弧的表达式包含了二阶函数和平方根等函数形式，处理起来都比较复杂，为了降低表达式的阶数、便于数据处理，对线段和圆弧采用参数方程的形式，见式(1)和式(2)。圆弧表达式以一阶三角函数代替了平方和开方计算。

(1)

(2)

1.1 线段与线段的混合

线段与线段的混合比较简单，几何上相当于两个向量的相加。混合后的参数表达式如式(3)所示：

(3)

式中，A、D为线段1斜率相关的系数；B、E为线段2斜率相关系数；C、F为线段起点坐标；t1、t2为线段1和线段2的变量，t1∈[θ1,θ2],t2∈[θ3,θ4]。

图1 线段与线段的混合

1.2 线段和圆弧的混合

线段和圆弧都属于最基本的几何元素，加工中的图案大部分由线段和圆弧组成。一般而言，图形组合是指多条线段和多条圆弧首尾相连拼接而成。图形的混合与此不同，是指将线段与圆弧合并为一个几何元素，并用其表示一段曲线。单个线段和圆弧混合基本表达式如式(4)所示。

(4)

式中，A、C为与线段斜率相关系数；B、D为曲线起点坐标;R为圆弧的半径值；t1、t2为线段和圆弧的自变量,t1∈[θ1,θ2],t2∈[θ3,θ4]。

在式(4)中，Rcosθ和Rsinθ是圆弧的参数表达；At和Ct是线段的参数表达。虽然t1、t2的取值范围是线性区间，但由于三角函数为无理函数，无法与一次项式进行合并。线段和圆弧的混合几何效果如图2所示，实线表示圆弧，点划线表示线段，虚线表示混合曲线。

图2 圆弧与线段的混合

1.3 圆弧和圆弧的混合

圆弧本身属于曲线，两段曲线的合成结果更具变化性。两段圆弧的混合曲线表达式如式(5)所示。

(5)

式中，R1、R2为两段圆弧的半径值；A、B为两段圆弧圆心相关的系数；t1、t2为两段圆弧的自变量，t1∈[θ1,θ2]，t2∈[θ3,θ4]。

式(5)中，两条圆弧的混合转换成了三角函数的和，t1、t2的取值范围依然是线性区间，混合的结果根据t1、t2的不同而生成不同的曲线。两个圆弧的混合几何效果如图3所示，实线表示圆弧1，点划线表示圆弧2，虚线表示混合曲线。

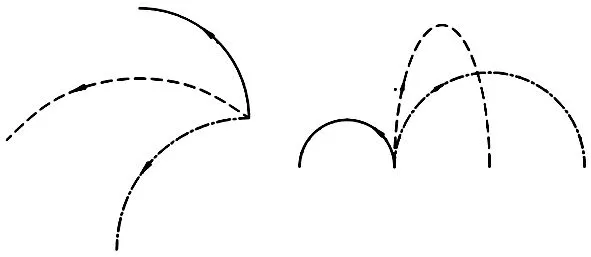
图3 圆弧与圆弧混合

2 一阶混合曲线的特例和归一化处理

2.1 混合曲线的特殊情况

线段与线段的混合结果还是线段，符合一般线段的特点。线段和圆弧、圆弧和圆弧的合成曲线则除了一般表达式外，在某些特点情况下可以退化为特定的曲线。

2.1.1 线段圆弧合成曲线特例

在式(4)中，取A=0，C=-R，θ和t的取值范围相同时，公式转换为式 (6)。

(6)

式(6)与摆线的表达式形式一致。根据摆线的定义，摆线为一个圆沿着一条线段运动时的轨迹，即一个整圆和一条线段的混合，见图2中右侧图形。由以上可得结论：线段与圆弧混合曲线在一定条件下可以形成摆线。

2.1.2 双圆弧混合曲线特例

如果R1=R2=R，根据三角函数的和差化积公式，式(5)可以转换为式(7)。

(7)

若t1-t2或者t1+t2为定值时，公式退化为圆的参数表达式。

若R1≠R2，t1+t2≡π时，根据三角函数诱导公式，公式(5)可以转换为公式(8)。

(8)

公式(8)与椭圆的参数公式相同，说明圆弧混合曲线在特定情况下可以形成椭圆，见图3中右侧图形。以上说明，双圆弧混合的结果是包含了圆和椭圆在内的一阶三角函数曲线。

2.2 曲线自变量的归一化处理

式(4)和式(5)中线段与圆弧的混合曲线包含三角函数，在区间内无限可导，符合光滑曲线的特征，其中的特例摆线和椭圆已经在工业中有很多应用。因此，线段和圆弧的一阶混合曲线在设计和加工应用中有很大前景。

混合曲线的变量较多，双元素混合时包含两个变量，虽然函数形式不同，但自变量的取值方法是一致的，即从区间初始值到最终值。对t1、t2进行归一化处理，即t1、t2统一为变量t，且t∈[0,1]。

(9)

将式(9)代入式(4)、式(5)中即可得到双元素混合的单变量表达式，见式(10)和式(11)所示。公式引入无量纲参数t，有利于对其进行各种变换和处理。

(10)

(11)

式中，α=θ1+(θ2-θ1)t，β=θ3+(θ4-θ3)t。

3 混合曲线的插补合成法

对混合曲线进行归一化处理之后，除了可以运用曲线插补算法对其进行插补外，还可以采用插补合成法。

3.1 插补合成法的定义和种类

插补合成法是先将插补对象分解为基本几何元素，然后分别对几何元素进行插补运算，最后把插补结果进行合成的插补方法。

式(3)～式(5)中曲线是由线段和圆弧混合而成的，因此插补方法可以对基本几何对象分别进行插补，然后再进行合成，即所谓的插补合成法。插补合成法分为在线插补合成法和离线插补合成法，其主要特征是根据插补过程是否在线来进行区分的。

3.2 在线插补合成法

在线插补是将加工信息发送给硬件插补器，硬件插补器进行实时插补。插补器运算一次得到一次插补运动，交给电机执行，然后再进行下一次插补运算。此方法可以利用现有的线段和圆弧的硬件插补电路，再辅助以分配器从而实现对混合曲线的插补运动。在线插补合成法电路功能框图如图4所示。

图4 在线插补合成器功能构成

以线段和圆弧混合曲线为例，在线插补合成器的工作流程如图5所示。获得混合曲线信息后进行分解，分解出来的信息发送给对应的线段和圆弧插补器，同时计算出各几何元素的插补步数并发送给插补分配器。插补分配器根据插补步数按照均布原则分别使各插补器进行运算，直至插补步数完成。插补过程中插补器运算一次完成后转换为保持状态，等待插补分配器的命令。在线插补的缺点在于无法在加工前得到具体的插补结果，只能依靠硬件算法的准确性。两个圆弧的混合曲线流程与图5一致，只需将线段插补器替换为圆弧插补器。

图5 在线插补合成法运算流程图

3.3 离线插补合成法

离线插补合成法是指在加工前进行插补运算并得到插补结果，在加工时直接输出插补结果数据，最后由硬件电路解码成电机的控制信号即可。离线插补的优势在于节省了实时插补运算的时间和资源，同时插补结果可以进行检查，以保证加工结果的准确。

离线插补的关键技术在于插补方法和插补结果的保存形式。由于线段和圆弧的插补方法很多，如逐点比较法、最小偏差法和数字积分法等等。因此，单个线段或者圆弧的插补可以采用任意种方法，不再详述。离线插补合成法的关键在于插补结果的保存形式，既要形式简洁，还要易于存储和编辑，使其能完成插补结果的合成运算。

4 插补合成法运算实例

由于离线插补合成的方法便于检验，因此以离线插补合成法结果来验证混合曲线的插补合成性。

4.1 离线插补格式保存——字节流

字节流格式易于保存离线插补尤其是软件插补的结果。字节流格式即以字节为最小单位，单个比特位为基本元素。一个比特位有两种含义，一种是表示进给与否，另外一种是表示正反方向。使用两个比特位保存一个轴的单步插补结果。一般机床都是多轴，根据机床的情况决定字节的格式。若是四轴以内的机床，以一个字节就可以囊括所有轴的单步插补结果；如果多于4个轴，将轴进行分组，将字节中的前几位设定为组号标识，一步可以多个字节表示。这些字节以十六进制字符串的形式储存在计算机中，读取的时候按照顺序进行。以两轴为例，单字节的格式如表2所示。

表2 单字节各个比特位含义(XY轴)

混合曲线中单个几何元素插补出来的结果以字节流的形式保存，然后进行合成。由于字节流非常适合编辑，因此插补结果的合成方法也比较简单。

以线段和圆弧合成为例，线段插补M步，圆弧插补N步，将两个字符串结合成一个字符串，流程如图5所示。将较长字符串设为基准，每读取一步增加一个步长。检测当前步长L是否大于1：若L>1，则读取较短字符串对应字节，同时补偿减1；若L<1，则继续读取较长字符串的字节。步长计算如图6所示(以M>N为例)。

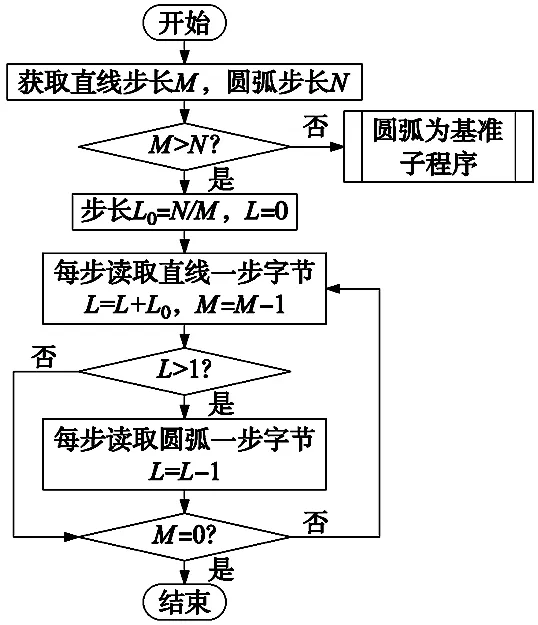
图6 运动字节流合成运算流程

4.2 加工对象

加工对象如图7所示，共4条曲线。曲线从原点(0,0)经过(2,1)、(13,0)和(2,-1)回到原点。其4段表达式见式(12)，取值范围第1段：t1:π→π/2,t2:0→1；第2段：t1:π/2→0,t2:0→10；第3段：t1:0→π/2,t2:0→-10；第4段：t1:(-π)/2→-π,t2:0→-1。相当于一个半径为1的整圆分成4个圆弧分别和线段混合。每段都可以分解为一段圆弧和一条线段的混合，适用于插补合成法。

(12)

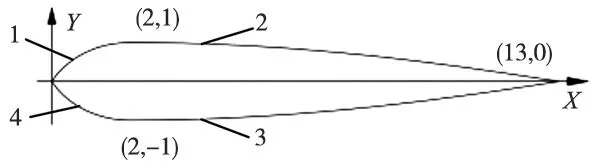
图7 线段与圆弧混合曲线加工对象

4.3 插补结果

使用VS2010中的C#语言进行编程开发，结果显示使用了开源图表控件ZegGraph。只需要对字节流进行读取，并转换为坐标点，添加到ZegGraph控件就可以显示插补结果。每段先对圆弧和线段分别进行插补，将插补结果保存成字节流的形式，再按照比例将两个插补结果进行合成，字节流形式的插补过程如图8示意。XY轴单个脉冲增量为1 μm，第1段圆弧插补1 414步，线段插补1 000步，合成结果共2 414步；第2段，圆弧插补1 414步，线段插补10 000步；第3段，圆弧插补1 414步，线段插补10 000步；第4段，圆弧插补1 414步，线段插补10 000步。离线插补总计27 656步。插补结果图形显示见图9，为了显示插补效果，Y轴选择较大比例，插补结果达到了加工要求。

图8 离线插补合成法流程示意

图9 插补合成法结果显示

以上是线段与圆弧混合曲线的插补实例，圆弧和线段的数量可以增加，组成更为复杂的一阶混合曲线表达式。具有混合特征的表达式完全可以进行插补运算，并使用插补合成法进行插补运算，结果完全符合加工要求。

5 结论

圆弧-线段一阶混合曲线具有圆弧和线段等元素的混合特征，表达式阶数低、几何含义清晰，不仅可以表示线段和圆弧，还包含了摆线和椭圆。在分析圆弧-线段一阶混合曲线的参数表达式的基础上，提出的插补合成法可以对其进行有效插补。无论离线还是在线的插补合成法结构清晰、过程简洁，数学运算量小，相对于样条曲线复杂的拟合插补过程有很大的优势。离线插补算法中使用的字节流表达形式简洁通用，便于数据存储和数据传输。