基于RecurDyn 和ANSYS 的液压挖掘机动臂结构优化设计

管琪明，解思状，贺福强，曹 刚

（贵州大学机械工程学院，贵州 贵阳 550025）

1 引言

液压挖掘机动臂结构的设计冗余影响着工作装置的可靠性和作业能力，需要对其结构参数进行优化设计。当前，国内外已有设计者对其进行研究。

文献[1]以动臂结构的刚度和强度为目标变量，实现了对动臂钢板厚度的双目标拓扑优化，使质量减轻了9.7%；文献[2]提出了一种基于进化结构优化（ESO）的箱体加强筋布置优化方法，该方法实现了对结构应力的有效改善。

文献[3]利用有限元模态分析对挖掘机回转立轴齿轮进行了结构强度分析和优化；文献[4]利用静力学分析的方法对铲斗强度进行了加强；文献[5]利用动力学仿真的方法减轻了结构的振动与冲击；文献[6]利用拓扑优化，减少了挖掘机臂截面应力；文献[7]利用有限元分析和NSGA-II 算法使驾驶室的避震器性能得到了提高；文献[8]应用D-H 法对四节臂轮式挖掘机工作装置进行了运动学分析，优化了动臂运动范围；文献[9]同时调用Solidworks 和ANSYS，对挖掘机工作装置静力学模型进行了集成优化；文献[10]经拓扑优化得到了材料分布的理想结构，实现了节材设计。

参考上述研究方法，以动臂实际承受的最大等效应力和抗弯系数为切入点，解决动臂的设计冗余问题。但动臂的应力和抗弯能力与其截面设计尺寸和钢板厚度均有关系，如果单一地改变设计尺寸或厚度进行优化，其结构可能仍然存在较大的冗余设计。其次，应力与设计尺寸、钢板厚度之间的关系也无具体数学模型，无法利用算法进行目标寻优。

为解决上述问题，采用动力学、静力学仿真对挖掘机动臂受力状态进行研究分析，预测推理动臂应力数学模型，结合动臂结构的抗弯系数，提出一种挖掘机动臂截面参数优化模型，利用遗传算法对截面参数进行双目标优化。

2 动臂受力仿真分析

利用动力学仿真软件Recurdyn 进行刚柔耦合模型建模及仿真，将动臂机构处理为柔性体，其余部分为刚体，为减少模型复杂程度，将发动机等机构等效为质量块，选取动臂弯曲处铰点旁边的截面为危险截面，如图1 所示。

图1 挖掘机刚柔耦合模型及危险截面Fig.1 Rigid Flexible Coupling Model and Dangerous Section of Excavator

在仿真时，将物料的质量附加在铲斗上，挖掘方式采用复合挖掘，利用STEP 函数对工作装置的运动进行定义，使其完成规定的挖掘动作，具体设置为：动臂液压缸：STEP（TIME，0，0，0.6，500）；斗杆液压缸：STEP（TIME，0.01，0，0.2，-100）+STEP（TIME，0.3，0，1.5，600）；铲斗液压缸：STEP（TIME，0.01，0，0.3，200）+STEP（TIME，0.4，0，1.5，-900）；函数中步幅的正负依据运动副的正方向设定。动臂各关键铰点C、B、D、F 的受力曲线图，如图2 所示。

图2 动臂铰点受力曲线Fig.2 Force Curve of Hinge Point of Boom

根据动力学的受力信息，选取动臂各个铰点的在Y、Z 坐标轴方向上的最大受力作为下一步动臂应力分析的试验参数。

3 试验及数值拟合

3.1 试验

选用ANSYS workbench 作为静力学分析平台，以工作装置挖掘过程中动臂在最低位置时的姿态为试验姿态，即动臂油缸全缩，动臂与斗杆铰接点、斗杆与铲斗铰接点、斗齿尖三点一线且垂直于停机面（简称姿态1）。在各个铰点的Y、Z 坐标方向上施加上一步动力学仿真得出的最大受力，通过设置单因素试验寻找动臂危险截面四个参数与等效应力之间的独立关系，具体参数，如表1（a）所示。

基于单因素关系式，对四个变量与动臂应力之间的多因素关系式作出预测，通过设置正交实验确认多因素关系式的相关系数，具体参数，如表1（b）、表1（c）所示。

表1 试验参数表Tab.1 Test Parameter Table

3.2 数值拟合

动臂最大等效应力与动臂危险截面高度h、截面宽度b、侧板厚度m、上下盖板厚度n 之间的数值拟合曲线，如图3 所示。其关系式为：

决定系数分别为 0.9916、0.9991、0.9985、0.8928；

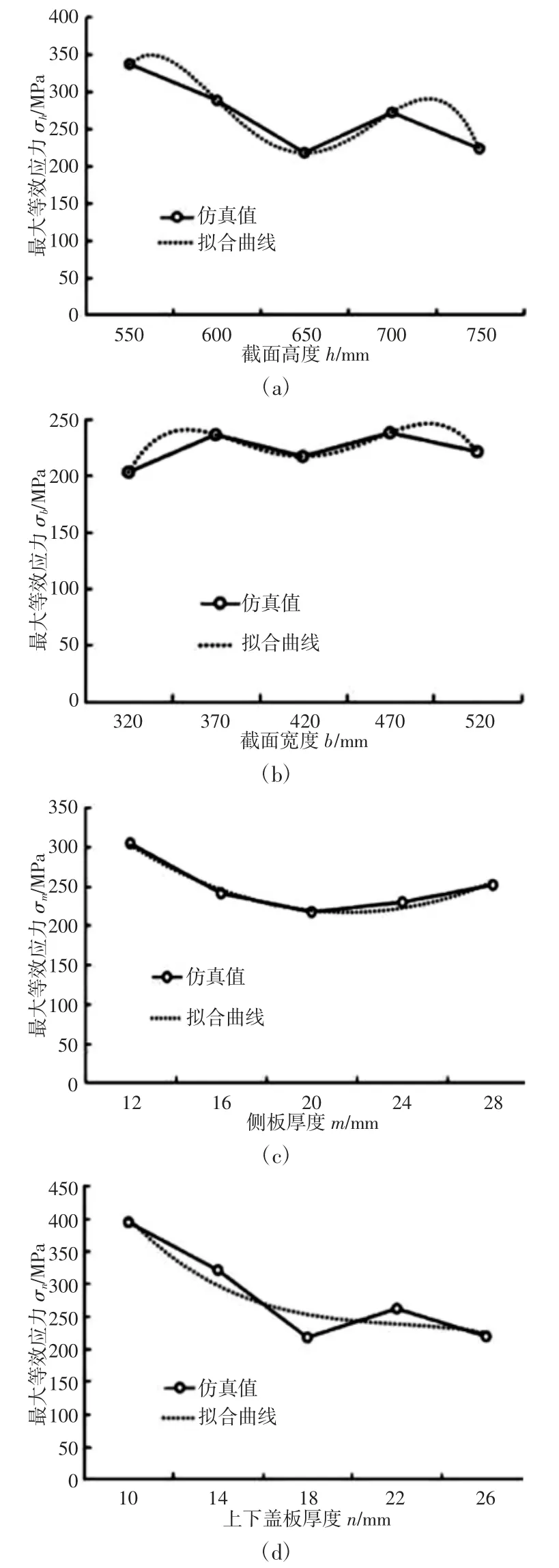
图3 单因素拟合图Fig.3 Single Factor Fitting Diagram

根据单因素数值模拟的结果，预测动臂最大等效应力关于截面参数的多因素模型表达式为：

其中：Ci、Di、Apq、Bpq、Cpq、d 均为常数。

对模型进行求解，设适应度准则为：

式中：σi—多因素模型值—正交试验值。通过变量求解，建立动臂最大等效应力与动臂危险截面参数的模型表达式为：

将表中的参数代入式（11）中，计算最大等效应力值σ，将正交试验值与计算值进行比较，验证多因素模型的误差大小。误差结果，如表2 所示。

表2 试验-模型计算误差表Tab.2 Test-Model Error Table

根据表2，试验值和计算值的平均误差为（-0.2864）%，误差较小，则式（31）多因素数学模型具有较高精度。

4 基于遗传算法的截面参数优化

4.1 目标函数

进行目标优化的表达式和约束条件分别为：

式中：Wi—动臂结构在仿真工况下实际承受的最大等效应力值；W2—抗弯截面系数，其表征截面的抗弯能力；W1与W2的乘积—动臂该截面处实际所承受的等效力矩值。

在动臂结构设计验算时，会根据理论最大挖掘力和铰点位置，估算动臂截面所需要承受的力矩，W1、W2在验算时为一对矛盾变量，但力矩计算比较麻烦，且误差较大。鉴于此，为了使截面抗弯能力最大发挥，以动臂截面的应力最小为第一个目标函数，为了使材料强度最大利用，以抗弯截面系数最小为第二个目标函数，由于设计选用材料为Q345 低合金钢，设计安全系数1.5，最大等效应力值应小于230MPa。为方便优化，考虑变量影响度差异，将单目标模型设定为：

选取初始种群大小M=100，最大进化代数T=100，变量个数v=4，变异概率Pm=0.1，交叉概率Pc=0.9，取单目标函数变化最小为适应度函数。

4.2 优化结果

结合限定条件，利用遗传算法进行优化，解得的最优值为h=631.2031，b=429.9503，m=21.5062，n=17.9317，适应度函数随进化代数的变化，如图14 所示。

图4 适应度函数变化曲线Fig.4 Variation of Fitness Function

将正交实验的结果、目前市场上小松挖掘机动臂参数的计算结果、遗传算法优化结果进行对比，如表3 所示。1 组为正交实验结果，2 组为小松挖掘机动臂参数的计算结果，3 组为遗传算法优化结果。

对比表中数据，3 组较1 组截面高度增大约31mm，盖板厚度减小2mm，但等效应力减小了11.5422%，3 组相对于2 组在截面高度和宽度上均有减小，侧板厚度增加约2mm，盖板厚度基本不变，等效应力减小9.3929%，3 组相对于前两组在截面系数上均有下降。

表3 优化结果Tab.3 Optimization Results

5 结论

（1）在动臂的最低姿态位置（姿态1），将动力学仿真得出的各个铰点在Y、Z 坐标轴方向上的最大受力施加在动臂各个铰点，利用静力学仿真进行单因素试验和正交试验，试验结果反映了动臂在最大受力情况下的最大等效应力，也反映了不同参数的变化对最大等效应力值变化的影响程度的不同；

（2）基于单因素试验结果，拟合出了最大等效应力关于各个变量的单因素数值模型，根据单因素数值模型预测了多因素复合模型，结合正交试验结果对多因素模型中的变量系数和常数进行了确定，得出了完整的多因素数值模型；

（3）结合多因素数值模型和抗弯截面系数公式，将最大等效应力最小值和抗弯截面系数最小值设为目标函数，利用遗传算法对动臂结构参数进行优化。优化结果显示，与正交设计和现存设计相比，W1分别下降了11.5422%和9.3929%，即抗弯能力得到了更大发挥，W2也相对降低，即材料强度得到了更大利用，此优化方法可为相关设计提供参考。