侧铣表面点位轮廓误差预测方法

罗 豪，余杭卓，江 磊，宋小欣

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

侧铣是指采用铣刀侧刃对工件进行铣削，常用于直纹面零件，是一种重要的数控加工方式。曲面的轮廓度误差是零件侧铣加工形位公差中应用广泛的评价指标之一。目前，轮廓度误差的测量和计算方法较为成熟，如文献[1]提出了一种用序列二次规划算法（SQP）解决定位问题，用迭代搜索法求解点到曲面最近距离；文献[2]采用分割逼近算法和遗传算法相结合的方法精确计算了复杂曲面的轮廓度误差；文献[3]采用粒子群算法解决了被测曲面和设计曲面的定位问题，同时简化了空间点到STL 模型距离的计算。

然而，在某些精密加工过程中，不仅仅需要测量加工后的轮廓度误差，更需要在加工前预测曲面的点位轮廓误差，从而进行工艺精度分析和补偿。

目前针对点位轮廓误差预测的研究较少，如文献[4]将利用五轴机床综合误差模型计算得到的各预测点投影到零件轮廓法向，得到点位轮廓误差，并分析了各误差因素所占的比重；文献[5]利用研发的五轴铣削加工精度预测软件系统计算得到切触点处的轮廓误差。但以上研究均将理想轮廓点与对应实际轮廓点的空间误差在法向上的投影作为点位轮廓误差，而在实际测量过程中，点位轮廓误差为理想轮廓点与实测点的空间距离，两者不一定相等，从而导致结果不够精确。

综合上述考虑，参考点位轮廓误差的测量原理，设计了一种侧铣表面点位轮廓误差预测方法。该方法利用侧铣扫掠面上的轮廓点阵列，采用NURBS 曲面拟合方法，构建了工件的理想和实际加工表面，再求取预测点法线与实际加工表面交点，即可求得待预测点位处的轮廓度误差。

2 侧铣扫掠面轮廓点阵列的计算

设刀位点在工件坐标系中的理想和实际坐标分别为PW（可由刀位文件获得）和（可根据多体系统理论和齐次坐标变换原理[6]，在考虑机床几何误差、工件位姿误差和主轴热误差等误差的条件下获得）。由于刀位点与刀具侧刃存在的几何关系，如图1 所示。以圆柱形铣刀为例，设刀具为理想刀具，刀位点为刀具底面中心点，刀具侧刃为刀具外轮廓母线，刀具侧刃垂直于刀具底面，且与刀位点距离一个刀具半径。因此选取刀具侧刃上等间距的若干点作为刀触点，就可以通过这种几何关系计算出刀位点对应的系列刀触点。

图1 侧铣加工示意图Fig.1 Diagram of Side Milling Process

刀位点对应的系列刀触点计算过程如下：

（1）设刀位轨迹上第i 个理想刀位点PWi的切向矢量为ti，根据PWi+1和PWi坐标关系，可知ti的计算公式为：

式中：xi，yi，zi—刀位点坐标，可由刀位文件获得；i—刀位点序列号。

（2）根据矢量叉乘原理，可知刀位轨迹法矢为：

式中：vi—刀位点对应的刀轴矢量，可由刀位文件获得。

（3）由刀位点和刀触点的几何关系可知，理想刀位点PWi对应的理想刀触点PCi为：

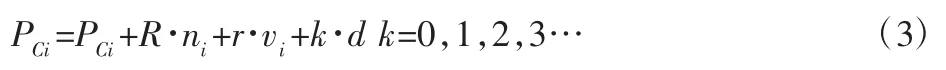
式中：R—刀具半径；d—两相邻刀触点之间的间隔，其大小为两相邻刀位点间隔的平均值；r—刀具圆角半径。

同理，计算出实际刀位点即可得到相应的实际刀触点。

侧铣扫掠面由刀具侧刃加工得到，扫掠面上轮廓点与刀具侧刃上的刀触点存在一一对应的关系。因此计算出每个位置刀位点对应的的系列刀触点，即可获得扫掠面上的轮廓点阵列。

3 点位轮廓误差预测

点位轮廓误差测量有接触式和非接触式两种，其中接触式应用的更为广泛。这里以接触式测量为例对点位轮廓误差的测量原理进行说明[7]。先通过工件三维模型获取理想加工表面上测量点P 及该点处法向矢量np，测头再沿着法矢方向接触到实际加工表面的点Pa，则点P 的轮廓度误差，如图2 所示。并且由于实际测量点Pa和实际轮廓点P′的连线不一定垂直于法向矢量np，因此点P 与点P′的空间误差在法向的投影不一定等于点位轮廓误差εp。

参考上述原理设计了点位轮廓误差预测方法，如图3 所示。假设理想加工表面为Sideal，实际加工表面为Sactual。点P 为Sideal上的一个预测点，该点的法向矢量为np，过点P 的法线L 与Sactual相交于点Pa，则预测点P 和交点Pa的距离即为点P 的轮廓度误差。

图2 点位轮廓误差测量原理图Fig.2 Diagram of Point Profile Error Measurement Principle

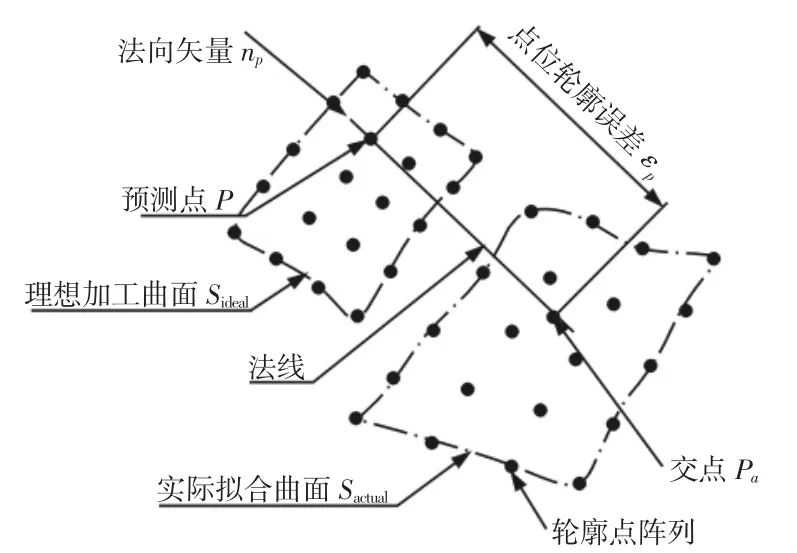
图3 点位轮廓误差预测示意图Fig.3 Diagram of Point Profile Error Prediction

3.1 加工表面的构建

通过上面的计算可以得到侧铣扫掠面的轮廓点阵列，这些轮廓点类似于接触式测量机在曲面上的采样点，因此可以采用曲面拟合方法构建加工表面。NURBS 拟合精度高，在工业制造中应用广泛，因此这里采用NURBS 曲面拟合方法。

将得到的轮廓点阵列当成型值点Pij（i=1，2，…，m；j=0，1，2，…，n），则一张 3×3 次 NURBS 曲面数学定义[8]为：

式中：Vi，j（i=0，1，2，…，m；j=0，1，2，…，n）—曲面的控制顶点；wi，j（i=0，1，2，…，m；j=0，1，2，…，n）—与控制顶点 Vi，j相联系的权因子；Bi，3（u）、Bj，3（v）—沿u 向的3 次和沿v 向的3 次B 样条基函数。

根据型值点数据计算节点矢量和基函数，反求控制点网格及权因子即可求出曲面方程。这样就可以分别得到理想加工表面Sideal（u，v）和实际加工表面Sactual（u，v）。

3.2 交点坐标的计算

根据上文分析可知，求得预测点 P（xp，yp，zp）和交点 Pa的距离即可求得点P 处的轮廓度误差，因此问题的关键为求取法线与实际加工表面的交点。交点坐标计算的具体步骤如下：

（1）计算理想加工表面上预测点P 处的法矢np：

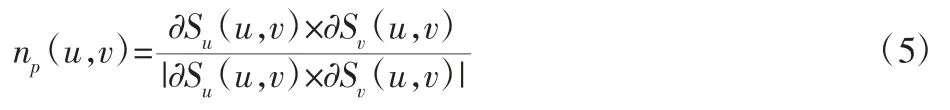
式中：Su（u，v）、Sv（u，v）—表示 u 向和 v 向的偏导矢。

（2）构建过点P 的法线L：

法线L 过点P，直线方向矢量为法矢np，则法线参数方程为：

（3）求解法线L 与实际加工拟合曲面Sactual的交点Pa[9]：

一般情况下，加工曲面NURBS 拟合时，控制点权因子计算结果为wij=1，则式（4）可简化为：

将曲面S（u，v）和直线L 所在坐标系变换为直线L 为Z 轴的坐标系，在变换后的坐标下，NURBS 曲面参数方程的控制顶点Vij（i=0，1，…，m；j=0，1，…，n）变换为NURBS 曲面方程变换为：

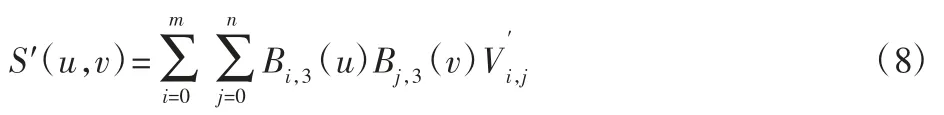
法线L 在新的坐标系下参数方程变为：

式中：z0—刀触点P 经过空间变换后的Z 坐标值。

图4 点位轮廓误差预测算法流程Fig.4 Algorithm Flow of Point Profile Error Prediction

在旧坐标系下求解法线L 与曲面S（u，v）的交点，转换为新坐标系下计算曲面S（′u，v）与Z 轴的交点。在新坐标下，交点坐标的 x 值和 y 值为零，即，则有：

采用拟牛顿迭代寻优[10]的方法解出方程组（10），就可以求解出法线L 与实际加工曲面Sactual（u，v）的交点Pa（xpa，ypa，zpa）。

完成了交点坐标的计算后，则预测点P 的法向轮廓误差为：

综上，可以计算出加工表面点位轮廓误差，算法流程，如图4所示。

4 实验验证

以XFYZBA 结构的五轴机床加工一个壁厚16mm 的S 形件（如图5）为例，验证预测方法的有效性。在加工前，需先采用激光干涉仪和球杆仪检测出机床几何误差和主轴热误差，计算出考虑这些误差的实际刀位点。在图示方框部分选取15（沿刀具轴线进给方向选取15 层）×20（沿铣削进刀方向选取20列）=300 个点，采用预测方法计算得到每个点对应的轮廓度误差预测值，预测结果，如图6 所示。

图5 S 件实物图Fig.5 S Pieces

图6 预测值分布图Fig.6 Diagram of Predicted Values Distribution

选取第一列15 个点，利用三坐标测量机得到对应的轮廓度误差测量值，并将其与预测值对比，对比数据，如表1 所示。数据显示预测值和测量值的差值都在0.006mm 以内。将数据做成折线图，如图7 所示。结果显示预测值与实测值变化趋势相同，从而验证了该预测方法的有效性。

表1 预测值、测量值及差值数据Tab.1 Data of Predicted Values，Measured Values and Difference

图7 预测值与实测值对比图Fig.7 Comparison of Predicted and Measured Values

5 结论

曲面加工工艺中有时也需要对点位轮廓误差进行预测，相关研究较少且与点位轮廓误差测量原理不符。针对这个问题提出侧铣表面点位轮廓误差预测方法，能够针对侧铣工艺在加工前对关键点位的轮廓度误差进行预测。并通过实际加工一个S 形件验证了该方法，结果显示通过该方法计算得到的预测值与实测值差距较小且分布大致相同，证明了该方法的准确性和有效性。该方法提高了点位轮廓误差的预测精度，能为加工质量评价和工艺规划优化提供重要的参考价值。