双螺杆真空泵新型变速螺线型转子的研究

魏蜀红，赵 峰，夏明川，王 君

（1.中国石油大学（华东）化学工程学院，山东 青岛 266580；2.中国石化青岛炼油化工有限责任公司，山东 青岛 266580）

1 引言

双螺杆真空泵因其抽气腔干式无油、运行平稳可靠和适应性强等优点，广泛应用于石油化工、食品制药、真空热处理、纳米制造和国防技术等领域[1]。双螺杆真空泵的主要部件是相互啮合的两个螺杆转子，螺杆转子及其转子截面型线的设计是其核心技术。目前传统的截面型线为摆线-渐开线型，采用圆渐开线和摆线连接齿顶和齿根圆弧[2]。然而，该型线存在尖点不能完全啮合，螺杆转子空间接触线存在断点，有明显的泄漏通道。为了改善该问题，文献[3-5]采用圆弧与摆线的等距曲线修正圆弧和圆渐开线连接处，并且在爪尖处也采用圆弧光滑连接，实现了转子的全啮合，但型线组成复杂。文献[6]为了消除泄漏通道提高密封性，采用多段圆弧及其包络线连接齿顶与齿根圆弧，增加曲线设计难度。文献[7]绘制了变螺距螺杆转子的啮合线和空间接触线。文献[8]研究了螺杆转子的热力变形和最大间隙变化情况。

针对以上问题，为了实现截面型线的光滑连接和简化设计，提出了一种变速螺线的构建理论，可用一条曲线光滑连接齿顶和齿根圆弧，推导了截面型线方程，对比了现有转子和所提出的新型螺杆转子的空间接触线和应力分布，对提高双螺杆真空泵的工作性能具有重要的意义。

2 型线理论

2.1 曲线啮合原理

螺杆转子截面型线的共轭曲线指的是在同步异向回转运动的任意时刻，另一转子截面型线上与已知截面型线完全啮合的曲线，假定第一截面型线上某一组成曲线的矩阵方程为r1（t），该曲线在运动时形成的曲线族可以通过坐标变换得到，曲线族的公式为：

式中：M12—动坐标系xO1y 到动坐标系xO2y 的变换矩阵：

式中：φ—截面型线的旋转角；求解t 与φ 的关系：

将式（3）带入坐标变换公式（1），即得到共轭曲线的方程。

2.2 变速螺线的构建理论

阿基米德螺线亦称为等速螺线，即一点P 沿动射线O1P 以等速率运动的同时，该射线又以等角速度绕点O1旋转，在图1 中表示为 v（t）=c1，ω（t）=c2。但由此不能光滑连接齿顶圆弧与齿根圆弧，通过改变点P 的运动方式，可以实现螺线在曲线交点处的光滑连接。

图1 变速螺线生成原理Fig.1 Generation Principle of Variable Speed Spiral

点P 的初始位置在半径为R3的齿根圆弧点A 处，终止位置在半径为R1的齿顶圆弧点C 处，如图1 所示。点P 沿射线O1P 做径向速度v（t）运动的同时，射线又以角速度ω（t）绕点O1旋转。且vA（t）=vC（t）=0，也就是在A 点和C 点处极径O1P 的增长速率为0，曲线曲率分别为R3和R1。

根据点P 在射线O1P 方向先加速后减速的运动规律，设径向速度v（t）为正弦函数：

则点 P 径向位移为：R（t）= ∫v（t）dt，将 R（0）=R3，R（θ）=R1带入上式，得到点P 位移方程为：

式中：θ—角度参数。

角速度ω（t）决定了点P 转过角度的快慢，点P 的旋转角函数为 φ（t）= ∫ω（t）dt。则得到变速螺线的方程：

图2 不同旋转角函数对应的变速螺线Fig.2 Variable Speed Spirals Corresponding to Different Rotational Functions

φ（t）可选取不同的函数，取 φ（t）分别为一次、二次、三次多项式时，且均通过点A 和点B，生成的三种变速螺线，如图2 所示。分别对应螺线 ABC1，ABC2，ABC3。由图中看出 φ（t）可以影响螺线圆心角和扫过的面积，可以对提高螺杆转子截面面积利用率提供一种途径。

3 新型截面型线

3.1 传统截面型线

传统截面型线，如图3 所示。由圆渐开线AB、齿顶圆弧BC、摆线CD 和齿根圆弧DA 组成。其在点A、点B 和点C 处存在尖点，容易引起应力集中；在A 点附近啮合不完全，存在如阴影所示的泄漏通道，造成压力损失和流量减小。

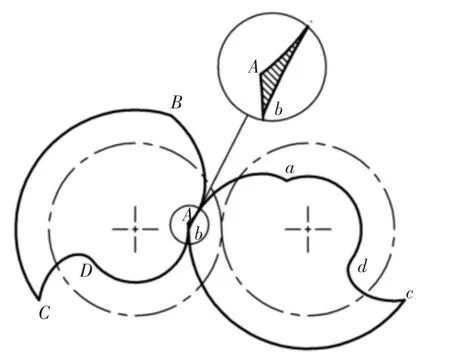
图3 传统截面型线Fig.3 Traditional Cross-Section Profile

3.2 变速螺线型截面型线

根据啮合原理和所构建的变速螺线，提出了一种变速螺线型转子截面型线，采用变速螺线替代圆渐开线，圆弧和摆线等距曲线代替摆线。为了使左右转子截面型线完全相同，AB 段采用变速螺线，BC 段采用变速螺线包络线。截面型线由6 条曲线组成：变速螺线 AB，变速螺线包络线 BC，三段圆弧（CD、DE、FA）和摆线EF，如图4 所示。

图4 新型截面型线Fig.4 New Cross-Section Profile

3.2.1 变速螺线及其包络线方程

变速螺线在构成截面型线时需顺时针旋转一个角度，使得点B 位于节圆和与横轴交点处，旋转角度的求解：

变速螺线AB 的方程可由式（6）顺时针旋转φ（θ/2）得到：

式中：M3—旋转矩阵：

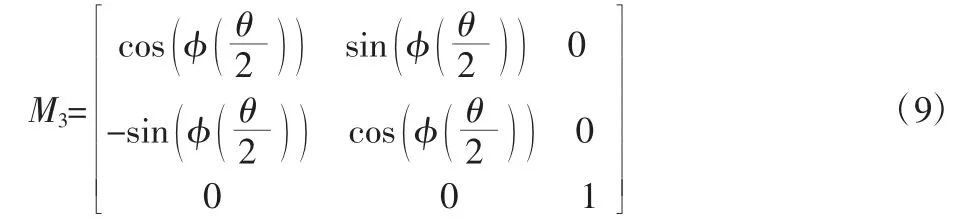
变速螺线包络线BC 方程由式（1）～式（3）求得：

3.2.2 旋转角函数的影响

点划线1、实线2 和虚线3 表示旋转角函数φ（t）为一次多项式t、二次多项式t+t2、三次多项式t+t2+t3对应的变速螺线AB 和变速螺线包络线BC，如图4 所示。三种螺线构成的型线面积明显不同，其各自的面积利用率，如表1 所示。随着旋转角函数φ（t）次幂的增加，变速螺线及其包络线组成的截面型线面积利用率逐渐增加。

表1 不同旋转角函数对应的面积利用率Tab.1 Area Utilization Ratios Corresponding to Different Functions

4 性能对比

在以下对比中变速螺线的旋转角函数均为φ（t）=t+t2+t3。

4.1 啮合特性分析

各段曲线的啮合线求解：

式中：M01—从动坐标系xO1y 到静坐标系XO1Y 的变换方程：

得到传统截面啮合线和变速螺线型截面啮合线，如图5（a）、图5（b）所示。

图5 截面啮合线Fig.5 The Meshing Lines of Cross-Section Profiles

4.2 空间接触线

空间接触线是双螺杆真空泵的主要泄漏通道之一，是由螺杆转子与转子之间非接触式啮合，转子与泵腔之间留有的间隙产生的。接触线两侧是压力不均的气体介质，如果接触线不连续，高压侧气体通过接触线缺口向低压侧泄漏，并且一般认为其长度越短螺杆转子的密封性越好。使传统截面型线转子和变速螺线型转子具有相同的转子齿厚，两种转子的空间接触线，如图6 所示。

图6 螺杆转子空间接触线Fig.6 Contact Linesof Screw Rotors

空间接触线是啮合线在螺杆转子曲面上的投影。啮合线不连续，如图5（a）所示。造成空间接触线在齿根和齿顶处有断点，如图6（a）所示。导致如图3 阴影处所示的泄漏通道。而变速螺线的啮合线和空间接触线是光滑连续的，如图5（b）、图6（b）所示。左右转子完全啮合，不存在泄漏通道，因而具有较好的级间密封效果。

4.3 应力分布

在双螺杆真空泵工作状态下，对传统螺杆转子和变速螺线型螺杆转子施加相同的边界条件。入口压力为3kPa，出口压力为100kPa，入口温度300K，出口温度370K，转速2940r/min。两种转子的应力分布，如图7 所示。

图7 螺杆转子的应力分布Fig.7 Stress Distributions of Screw Rotors

应力多集中于齿根处，最大应力值位于出口端齿根处。传统截面型转子最大应力值为35.26MPa，局部放大图处齿根应力集中明显，取一点值为7.73MPa，如图7（a）所示。变速螺线型转子最大应力值为32.76MPa，较传统截面型转子减小7.09%，局部放大图处没有应力集中，应力分布更为平缓，取相同的点应力值为5.55MPa，也小于传统截面型转子，如图7（b）所示。这是因为传统截面型转子齿根面与斜齿面之间过渡曲率突变较大，变速螺线型转子能够完全光滑过渡。

5 结论

（1）提出了一种变速螺线的构建理论，求解了其方程形式，该螺线可光滑连接齿根和齿顶圆弧，此理论对爪式真空泵、罗茨风机和滑片真空泵等流体机械有一定的应用价值。

（2）提出了一种变速螺线型转子截面型线，采用变速螺线及其包络线替代传统截面型线的圆渐开线，解决了截面存在尖点的问题，旋转角函数次幂增加时，转子截面的面积利用率有所提高。

（3）变速螺线型转子相比于传统截面转子具有光滑连续的啮合线和空间接触线，不存在泄漏通道，因而具有较好的级间密封效果；齿根应力分布更为平缓，最大应力值减小7.09%，转子受力情况好。