深圳某整体桥受力性能分析

张 嵩

（深圳市交通公用设施建设中心 深圳518000）

0 引言

相关学者研究表明，我国现有的公路桥梁中，有超过70%都存在伸缩缝破损和桥头跳车等问题［1］。全国每年因修理、更换伸缩缝产生的费用非常惊人，而由此造成交通中断等带来的间接损失可能更大［2-3］。目前，桥台位置取消伸缩装置或伸缩缝的做法，主要包括延伸桥面板桥台、整体式桥台和半整体式桥台，从3 种无缝桥在国外的应用数量和使用效果上来看，整体桥的应用数量最多，应用范围最广，并且整体桥能够完全取消支座、伸缩缝和伸缩装置，实际使用效果最好［4-5］。结构与土的共同作用［6-7］是整体桥受力分析的关键，其情况较为复杂，截止到目前，国内外还没有公认的、成熟的设计原则和标准［8］。工程应用中，需结合本地的具体实际，在工程背景下开展应用研究。本文将整体式桥台桥梁作为研究对象，以深圳某整体桥为背景，分析整体桥的受力性能，验算桥梁的安全性、稳定性和可靠性。

1 工程概况

深圳市南坪三期快速路工程位于龙岗区和坪山区，全长22.2 km，连接了南山、福田、龙华、龙岗和坪山，使得坪山到深圳市中心的距离进一步缩短，从原来的1.5 h 缩短至40 min。某整体桥是南坪快速路三期项目的子工程，经过某公园，桥址处对生态环境保护的要求高，客观条件要求桥梁结构设计必须具备以下特点：①最大限度减少桥梁养护维修的次数和费用；②较快的施工进度。通过调研国内外整体桥的使用情况，最终决定采用无伸缩缝整体式桥台桥梁。

1.1 桥型布置

桥梁分为左、右两幅桥，为28.96 m+30.00 m+28.96 m=87.92 m 连续结构箱梁，取消了伸缩缝和支座的设置，如图1所示。

图1 某整体桥桥型布置Fig.1 Layout of the Integral Abutment Bridge

1.2 主梁横截面

桥梁主梁为单箱三室箱梁，宽17 m，横断面布置为：0.5 m（栏杆）+16.0 m（行车道）+0.5 m（检修道及栏杆）=17.0 m，单向横坡为2%，单箱底宽3.95 m，箱梁两侧悬挑长度为2.25 m，悬挑端部板厚20 cm，根部板厚40 cm，箱梁顶板标准厚度为25 cm，横梁周围1.2 m 范围内的顶板加厚至45 cm。桥梁横断面如图2所示。

图2 某立交主线桥主梁横断面Fig.2 Cross Section of the Certain Main Bridge Girder

2 结构模型、荷载及主要输入参数

2.1 结构计算模型

按照设计图纸，将结构离散为593 个单元，614 个节点，利用Midas/Civil 建立分析模型。桩土作用和台后被动土压力采用土弹簧模拟，按照《公路桥涵地基与基础设计规范：JTG 3363-2019》［9］中的m 法计算土弹簧刚度。主梁与桥台采用刚性连接模拟整体式桥台与主梁固结，主梁与桥墩采用刚性连接来模拟墩梁固结，桩底为固结。全桥有限元模型如图3所示，施工工况如表1所示。

2.2 主要材料

主梁及墩台、桩基的混凝土强度等级分别为C50、C30 和C40，主梁采用1860 钢绞线，全桥均采用HRB400钢筋，材料强度参考《公路钢筋混凝土及预应力混凝土桥涵设计规范：JTG 3362-2018》［10］。

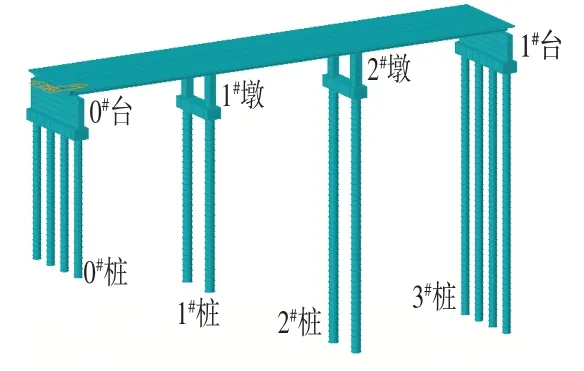
图3 主桥分析模型Fig.3 Analysis Model of Bridge

表1 施工信息明细Tab.1 Construction Information Details

2.3 设计荷载

本桥恒载包括主梁的自重和二期恒载，汽车荷载等级是城-A 级，采用4车道，荷载取值参照《城市桥梁设计规范：CJJ 11-2011》规定选取。冲击荷载中，计算连续梁冲击力引起的剪力效应和正弯矩时，采用f1；计算连续梁冲击力所引起的负弯矩效应时，采用f2。f1、f2的计算公式如式⑴：

式中：l 为结构的计算跨径，当连续梁的跨径不等时，取最小跨的计算跨径；E是结构材料的弹性模量，组合截面时，需计算等效弹性模量；Ic为结构跨中截面的截面惯矩；mc为线质量；二期荷载不考虑质量的贡献。

整体温度差按整体升温25 ℃，整体降温-25 ℃计算，升温、降温的梯度模式参照《公路桥涵设计通用规范：JTG D60-2015》［11］规定；不均匀沉降为10 mm；汽车制动力参照文献［11］取值。

2.4 边界条件

2.4.1 桩基水平弹簧刚度

在MIDAS建模模拟中，根据式⑵计算桩基水平弹簧刚度。

式中：y 表示侧向位移；Kp表示被动土压力系数；Pu表示极限抗力；γ'表示地基土的有效重度，对干砂取天然重度，对饱和取浮重度；z表示地基土的深度；D为桩径；Kh为地基土模量系数。

2.4.2 台后土压力的模拟

Midas 软件中台后填土的土压力计算采用静止土压力加上仅受压的非线性土弹簧（考虑被动土压力）模拟，升温时为横向弹性土抗力加上静止土压力，降温时则为主动土压力，桥台及承台的静止土压力如图4所示。

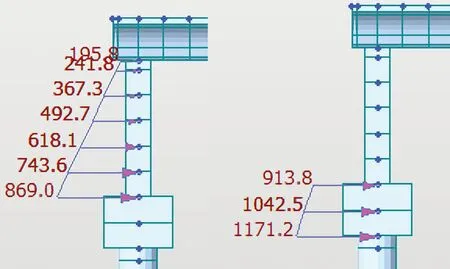
图4 桥台及承台静止土压力Fig.4 Static Soil Pressure Distribution of the Abutment and Cap

台后被动土压力采用仅受压的非线性土弹簧模拟，如图5所示。

图5 台后被动土压力模拟示意图Fig.5 Schematic Diagram of Passive Earth Pressure behind the Abutment

2.4.3 桩底及上下部连接方式

桩底及桥台处主梁与桥台、主梁与桥墩均采用刚性连接模拟固结状态。

3 结构受力分析验算

3.1 主梁结构验算

3.1.1 持久状况下的承载力极限状态验算

承载力极限状态下的主梁正截面抗弯承载力验算结果如图6 所示，可以看出正截面抗弯承载力验算满足《公路桥涵设计通用规范：JTG D60-2015》［11］要求。

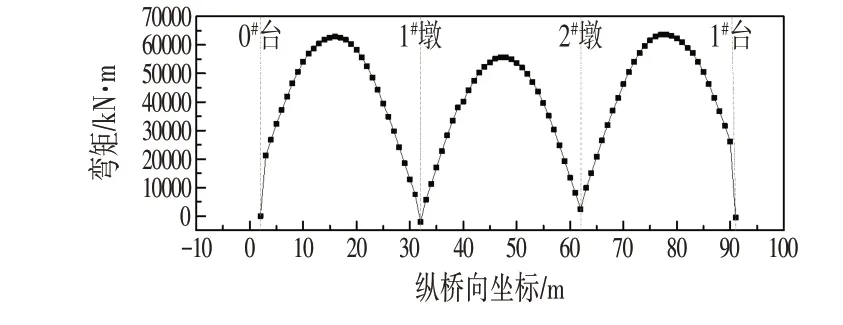
图6 承载力极限状态组合下主梁正截面验算结果Fig.6 The Checking Calculation Results of the Girder’s Normal Section under the Bearing Capacity Limit State

图7 所示为斜截面抗剪承载能力验算结果，表明全桥所有截面满足斜截面抗剪承载能力验算。

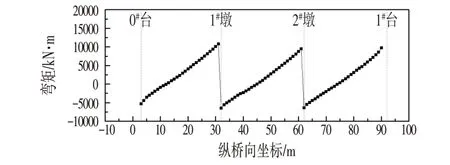
图7 承载能力极限状态组合下主梁抗剪截面验算Fig.7 The Checking Calculation Results of the Girder’s Shear Section Under the Bearing Capacity Limit State

3.1.2 持久状况下的正常使用极限状态验算

对于顶缘、底缘混凝土抗裂验算，参照文献［10］的规定，A 类预应力混凝土构件，在短期效应组合下应满足式⑶要求：

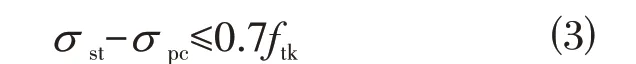
式中：σst为在短期效应组合下构件抗裂验算边缘混凝土的法向拉应力；σpc为扣除全部预应力损失后的预加力，在构件抗裂验算边缘产生的混凝土预压应力；ftk为混凝土的抗拉强度标准值。

正常使用的短期效应组合作用下所有截面顶缘、底缘拉应力如图8所示，均未超过容许拉应力。

对于A 类预应力混凝土构件，还应按文献［10］规定对构件进行斜截面主拉应力验算：

图8 正常使用短期效应组合作用下主梁应力Fig.8 Main Girder Stress Under Normal Use Short-term Effect Combination

式中：σtp为由短期效应组合和预加力产生的混凝土主拉应力。

正常使用短期效应组合作用下所有截面的拉应力如图9所示，均未超过容许拉应力，满足要求。

图9 斜截面主拉应力验算Fig.9 Checking Calculation of Principal Tensile Stress of Oblique Section

变形参照文献［10］规定进行验算，主梁变形如图10所示，主梁短期效应最大位移为22.18 mm，使用阶段的挠度需考虑荷载长期效应的影响，需乘以挠度长期增长系数（ηθ=1.425），得长期挠度值为31.61 mm，文献［11］规定的容许值为计算跨径的1/600，即50 mm，满足要求。

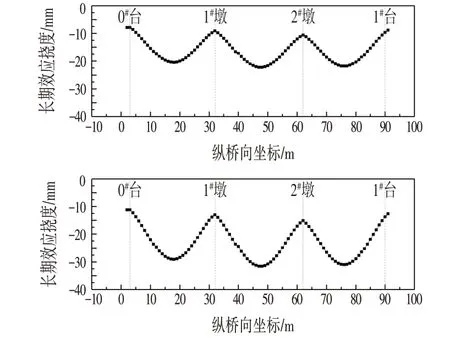
图10 正常使用阶段的主梁最大挠度分布Fig.10 Distribution of Maximum Deflection of Main Beam during Normal Use Stage

3.1.3 持久状况和短暂状况下构件的应力验算

持久状况顶板、底板混凝土压应力验算参照文献［10］规定，对于A 类预应力混凝土构件，标准效应组合下，应满足式⑸要求：

式中：σkc为混凝土法向压应力；σpt为由预加力产生的混凝土法向拉应力；fck为混凝土轴心抗压强度标准值。

在标准效应组合下，主梁各截面顶缘、底缘的压应力如图11 所示，可看出均在限值范围（-16.2 MPa）内，满足要求。

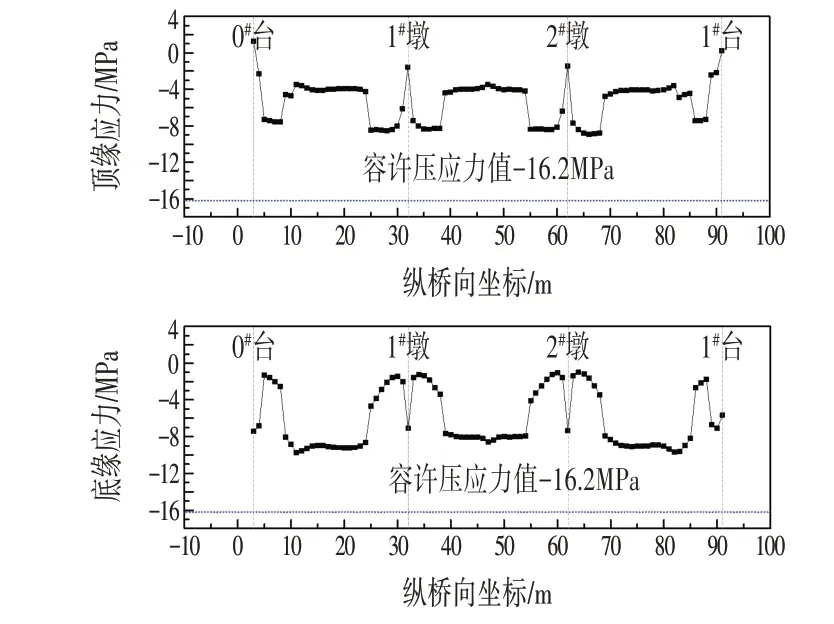
图11 标准效应组合下主梁的最大压应力验算Fig.11 Checking Calculation of Maximum Compressive Stress of Main Beam under Standard Effect Combination

对于A 类预应力混凝土构件，还应进行构件斜截面的主压应力验算，应满足式⑹要求：

式中：σcp为预应力浑南凝土受弯构件由作用（或荷载）标准值和预加力产生的混凝土主压应力；ftk为混凝土的抗拉强度标准值。

截面在正常使用短期效应组合作用下的主压应力如图12所示，均未超过规范容许压应力。

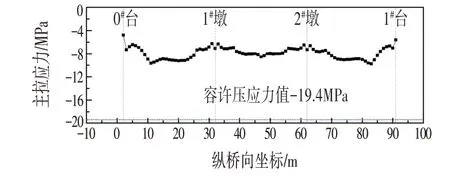
图12 斜截面主拉应力验算Fig.12 Checking Calculation of Principal Tensile Stress of Oblique Section

预应力钢筋验算参照文献［10］规定，对钢铰线、受拉区预应力钢筋的最大拉应力应满足0.65×1 860=1 209 MPa。预应力钢束最大拉应力计算结果如表2所示，从表2中可以看出，均符合文献［10］要求。

施工阶段的混凝土应力验算参照文献［10］规定，各主要施工阶段箱梁的顶缘、底缘应力如图13 所示，可看出各施工阶段箱梁顶板、底板应力均满足文献［10］要求。

3.2 主桥下部结构验算

3.2.1 主桥桥台桩基验算

参照文献［10］的相关规定，应按不同部位进行下部结构的承载力极限状态验算和正常使用极限状态验算，桥台桩基受力验算包括：桩身强度验算、裂缝宽度验算。

表2 预应力钢束参数与验算Tab.2 Prestressed Steel Bundle Parameters and Check Calculation

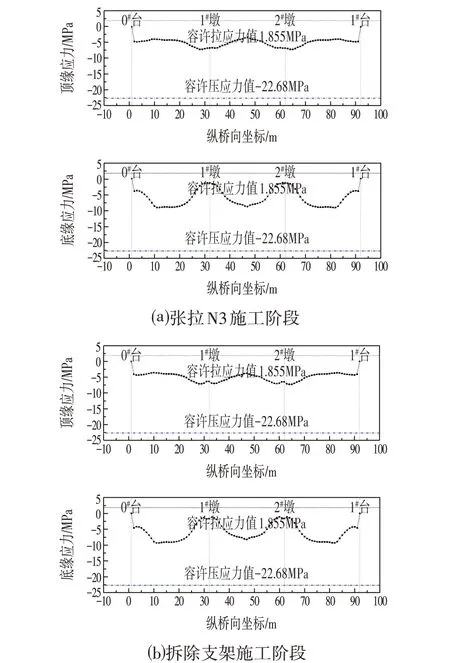
图13 主梁上、下缘正截面混凝土应力Fig.13 Stress of the Normal Section Concrete at the Upper and Lower Edges of the Main Beam

⑴桩基承载力验算：3#台为摩擦桩，参照《公路桥涵地基与基础设计规范：JTG 3363-2019》中规定来验算桩基承载能力：

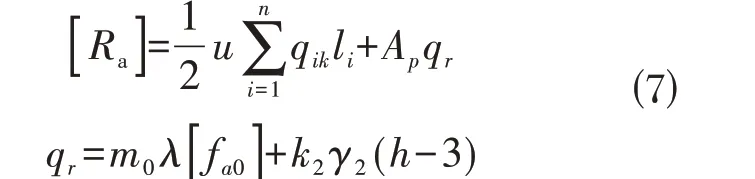
式中：［Ra］为单桩轴向受压承载力容许值；u 为桩身周长；Ap为撞断截面面积，n为土层数；li为承台地面或局部冲刷线以下各土层的厚度；qik为与对应的各土层与桩侧的摩阻力标准值；qr为桩端土的承载力容许值；［fa0］为桩端处土的承载力基本容许值；m0为清底系数；λ 为修正系数；k2为容许承载力随深度的修正系数；γ2为桩端以下各土层的加权平均重度。

代入数据计算得到［Ra］=20 757.10 kN＞5 739.0 kN；单桩承载力设计值小于容许承载力。

⑵桩身强度验算：取桥台桩基进行桩身强度验算，包括：轴力最小时的轴心受压验算、轴力最小时的偏心受压验算、主弯矩最大时的偏心受压验算和主弯矩最小时偏心受压验算。验算结果如图14～图17 所示。可知桩身强度满足要求。

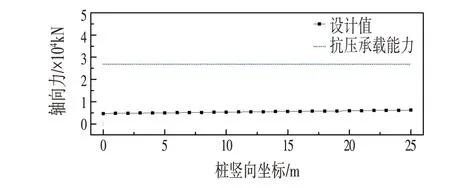
图14 轴心-Fxmin：轴力最小时的轴心受压验算Fig.14 Calculation of the Axial Compression When the Axial Force is the Smallest

图15 偏心-Fxmin（My）：轴力最小时的偏心受压验算Fig.15 Eccentric Compression Check when the Axial Force is the Smallest

图16 偏心-Mymax：主弯矩最大时的偏心受压验算Fig.16 Eccentric Compression Check when the Main Bending Moment is Maximum

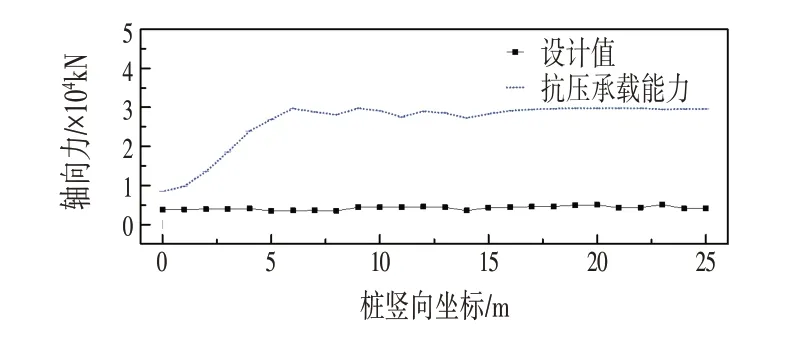
图17 偏心-Mymin：主弯矩最小时偏心受压验算Fig.17 Eccentric Compression Check when the Main Bending Moment is Minimum

3.2.2 下部结构裂缝宽度验算

对桥墩、桥台和桩基进行裂缝宽度的验算，验算结果如图18 所示，由图18 可知桥台端墙和桩基以及桥墩墩柱和桩基裂缝宽度验算满足要求。

图18 裂缝宽度验算结果Fig.18 Crack Width Check Result

4 结论

整体桥是目前应用最为广泛的无缝桥，可以从根本上取消梁桥的伸缩装置，从而增强桥梁的耐久性能，降低后期养护维修费用和社会不良影响，提高行车的舒适性，适应交通重载化的实际情况，避免地震作用下的落梁危害以及改善桥头跳车问题，具有广阔的市场前景和显著的经济效益。

本文采用有限元软件Midas建立了考虑桩土共同作用的全桥杆系有限元模型，分析了整体桥受力性能，依据国内现行规范，验证了该桥的设计、施工是安全、可靠和稳定的，有助于解决此类结构在设计和施工过程的关键性技术问题，具有一定的工程应用和推广价值。