阶估计法在判断瑕积分审敛法中的应用
2021-01-27张祖叙孙荣璞尹凯倩
张祖叙,孙荣璞,尹凯倩
(山东科技大学数学与系统科学学院,山东 青岛 266590)
通过对微积分的学习,可以利用比较原则、柯西判别法、狄利克雷判别法和阿贝尔判别法等[1]来判断瑕积分的敛散性。从判别法的不同角度对阶估计法进行研究,得到审敛性的定理。已有研究者对判别法进行过细致而全面的研究,如齐紫微[2]等学者给出的基于阶估计法的无穷广义积分审敛性定理。我们通过阶估计法推导了判断瑕积分敛散性的判别法,并通过比较判别法进行证明并附以实例,验证了审敛法的有效性和实用性。
1 基于阶估计法的瑕积分审敛性判别法
定理1.设f(x)是定义在区间(a,b]上的非负可积函数,且满足:



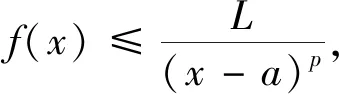
易见瑕积分收敛,由比较判别法,瑕积分同样收敛。
②当p≥1时,经过计算可知:

小结:在微积分学中只讨论了分式的奇点为0的判别法,而定理1给出了分式的起点不为0的一般情况。
定理2.设f(x),g(x)是定义在区间(a,b]上的非负函数,则:



证明:

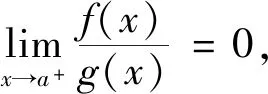

小结:与定理1提出的思路相一致,根据由特殊到一般的数学思想,对微积分学中的原有积分进行了简单推广。
定理3.设f(x)是定义在区间[a,b)上的非负可积函数,则:
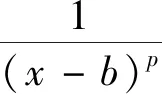
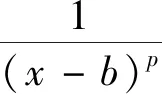
证明:
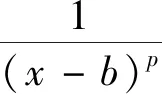
①0 ②p≥1时: 结合①②两点,得到了定理3的证明。 小结:定理3对应于微积分学中广义积分的阶判别法,将广义积分调整为积分区间为半闭半开区间的瑕积分。 定理4.设f(x)是定义在区间(a,b)上的非负可积函数(a和b都是瑕点),且对于∀p∈(0,1)及c∈(a,b),满足: 证明: 小结:与定理3相比较,发现积分区间两端均为瑕点。在证明该定理的过程中,对给定的积分区间进行分段,从而归结为定理3的结果。 又因为tanx~x(x→0),ex-1~x(x→0),所以有: 解: 根据瑕积分阶估计法,推广了微积分学中分式奇点为0的一般情况,并提高了阶估计法的适用范围,通过实例的引入,验证了审敛法的有效性和实用性。


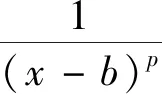

2 定理应用
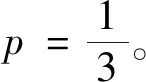



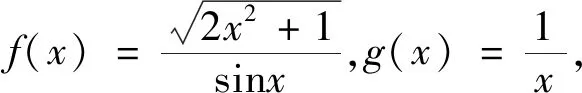
3 结语
