应用KPK力学方法研究落体的运动

皇甫泉生，严非男，顾铮

（上海理工大学 理学院，上海 200093）

自从牛顿揭示了力是改变物体运动状态原因的本质之后，人类对自然的认识发生了一大飞跃，引领力学走上了正确的道路，取得了辉煌的成就，牛顿关于力的三大定律成为了经典力学的基本定律。但是物理学的各分支沿着各自的道路发展，使经典物理学的各分支学科之间缺乏基本的相似性和类比。德国卡尔斯鲁厄物理课程[1-2]（KPK）开发者全面梳理了经典物理学中的知识体系，在力学中引入了动量流强度的概念，将物体之间的相互作用看成是动量的流动，而动量流强度就是经典力学体系中的力，构建了与经典力学等价[2]的卡尔斯鲁厄物理课程的力学体系，使力学与电学有了基本的相似性，可以进行广泛的类比[3-4]。类比的思想方法在教与学和创新中起到的启示作用是非常积极的，而KPK物理课程在这方面的优势是毋容置疑的，常言说“他山之石，可以攻玉”，如果希望将这一新的力学体系运用于我们的教学中，需要我们深入学习和研究KPK物理课程，充分地进行探索实践、消化吸收、掌握KPK的力学体系。落体是生活中较常见的运动物体，这里不妨通过用KPK力学方法来解决落体中的一些问题，作为运用KPK力学体系的一次探索实践。

1 卡尔斯鲁厄物理课程的力学体系

卡尔斯鲁厄物理课程（KPK）的开发者全面地审视了经典物理学，仔细地梳理其中的物理量，将描述物体运动状态的物理量分成与总质量成正比的广延量和与总质量无关的强度量，并在其中选择与能量密切相关的广延量动量和强度量速度作为力学分支的中心物理量[5]，分别与电学分支中的广延量电荷量和强度量电势进行类比，并将物体之间的相互作用看成是因为有动量在它们之间流动的结果。在电学中单位时间内流过某一截面的电荷量定义为电流强度I=dq/dt。式中：q表示电荷；t表示时间。同样，在KPK中把单位时间内流过某一截面的动量定义为动量流强度Ip=dp/dt。式中，p表示动量。对照牛顿第二定律，物体所受合力F=dp/dt。可见KPK中动量流强度就是经典力学中物体之间的相互作用力[6]。如果有两个物体发生了碰撞、滑动摩擦等相互作用，每个物体的动量都会发生变化，并且其中一个物体的动量增加量一定等于另一个物体动量的减少量，可以认为动量从一个物体流出并流入了另一个物体。在KPK的力学体系中认为动量守恒定律是力学的基本定律，动量可以在物体之间流动，但总量保持不变，即从一个物体表面流入物体的动量流强度必定等于该物体的动量变化率。将其推广到物体系，就意味着我们可以在空间任取一物体系闭合曲面，单位时间内流入该物体系曲面的动量，必定等于该物体系曲面所包围的空间区域内物体的动量的单位时间增量，可见动量守恒定律就是动量的连续性方程：dp/dt，也就是牛顿第二定律。因此在KPK中解动力学问题是先对研究对象进行动量流分析：动量流入、流出的途径有那些？大小是多少？方向向哪里？然后根据动量连续性列方程求解。需要注意的是动量是矢量，动量流也是矢量，动量的连续性方程是矢量方程。

灯笼被用来营造喜庆的氛围，节假日随处可见悬挂的红灯笼。对于如图1所示悬挂灯笼的系统，学过物理的人都知道，这是一个平衡系统，在教学中至少会提到有4个力。它们分别是：通过引力场作用在吊灯和地球之间的一对相互作用力，为万有引力；以及通过悬绳作用在吊灯和支架之间的一对相互作用力，它们是弹力。每一对力都遵循牛顿第三定律，而作用在灯笼上的两个力构成了一对平衡力，这4个力的大小都相等，但名称并不相同。

图1 悬挂的灯笼Fig. 1 Hanging lanterns

当我们把动量想象成与水一样是可以流动的物质，而力实际上就是动量流，那么这个悬挂灯笼的系统就会这样来描述了：动量从地球流出，经过引力场流入灯笼，再从灯笼流出，经过悬绳流入支架然后流回到地球。这里相当于一个闭合回路，在其中流动的是动量，没有任何地方有动量的累积，因此各处的动量流强度都相等，每个物体的动量不变，灯笼系统保持静止状态。这样的描述简洁明了，也不会对回路中“各处的动量流强度都相等”产生异议。反观在牛顿力学中，引入了4个力而名称各不相同，相当于把同一水流中4处不同位置的水用了4个不同的名字来命名，不仅是没有必要的，反而还增添了麻烦：为了消除“名称不同的力但是大小相同”的困惑，还要用一个定律来确定其中的每一对作用力与反作用力相等。

在KPK力学体系中力就是动量流强度，力的作用遵循动量连续性方程，那么容易得到，在经历了一段时间的积累，流入某个闭合曲面动量必定等于该闭合曲面动量的增量。动量在流动时也会携带着能量一起流动，从而起到传递能量的作用，因此动量被称为能量载体[7-8]，它所传递的能量E为：式中：r表示运动物体的位置；v则是该物体的运动速度。可见动量流的空间积累效应就是能量流。把单位时间内流过某一截面的能量定义为能量流强度IE=dE/dt，而动量在携带着能量所形成的能量流强度为：IE=dE/dt=v·dp/dt=v·Ip=v·F，可见动量在流动过程中传递的能量流强度就是我们熟悉的功率。

2 对落体运动速度的计算

对于我们生活中常见落体，在中学阶段只考虑重力的作用，在大学阶段还要考虑空气的摩擦阻力作用。设有一质量为m的小球由静止开始下落，如果我们要确定它的速度随时间变化的规律，在经典力学中，解题的顺序通常是先对研究对象进行受力分析，然后根据牛顿定律列方程求解[9]。在KPK中力就是动量流，解题的方法是先分析对象的动量流，然后根据动量的连续性列方程求解。

取向下为动量正方向，对小球进行动量流分析：因小球处于重力场内，因此有动量流强度FG=mg从地球经重力场流入小球[10]，式中，g为重力加速度。小球因为运动与空气发生摩擦，会有动量的流失。一般认为因空气摩擦而引起小球的动量流失与速度成正比（即摩擦阻力与速度成正比），设比例系数为k，因此有动量流强度Fm=kv从小球流出进入空气，如图2所示。

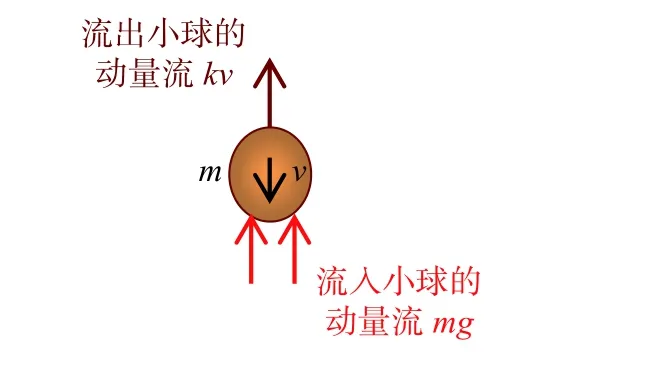
图2 落体的动量流图Fig. 2 Momentum flow diagram of a falling body

根据动量连续性可确定：流入小球的总动量流强度等于小球的动量变化率，即：mg-kv=

当t→∞时，解得收尾速度：

可见一个在空气中下落的物体，尽管从重力场流入物体的动量流强度是恒定的，使物体的动量稳定地增加。但由于物体与空气之间存在着摩擦，导致动量的流失，流失的动量流强度随着物体运动速度的增加而变大。一旦流入物体的动量流强度等于流出物体的动量流强度，小球的动量将不再变化，达到一个稳定的速度，此时物体的速度称为收尾速度（也称极限速度）。收尾速度的大小与k有关，而k主要取决于物体的外形和自重。例如毛毛细雨飘飘然润物无声，收尾速度不到1 m/s，而暴雨则掷地有声，雨滴最大直径5.5 mm左右，最大收尾速度可以达到8～9 m/s。

如果没有空气的摩擦，就不会有动量从物体流出进入空气，但始终有动量从地球经重力场流入物体，因此物体就不会有收尾速度。月球上没有大气，因此所有物体都以同样的加速度坠落，一片羽毛与一块石头只要从同一高度出发，就会以同样速度落向月面。在地球上，如果我们把羽毛与小块石头放入抽成真空的玻璃管中，同样能观察到这一现象。

3 对跳伞员的速率分析

高空跳伞是一项体育运动，跳伞员可以通过操纵变换出各种表演花样，令人赏心悦目。撇开各种操纵因素，高空跳伞员相当于有水平初速度为v的落体，跳伞员动量变化的途径只有两个：由重力场流入的动量和因为摩擦而流失的动量。但是因为跳伞员从飞机上跳出时有水平速度，因此牵涉到两维运动，情况变得相对复杂，且一般飞机飞行速度都大于跳伞员的第一收尾速度（没有开伞时的收尾速度约50 m/s）时,则跳伞员的速率变化将更加丰富，值得探讨。

跳伞员由于运动，与空气发生摩擦而流失的动量的状况比较复杂，参照文献[11]，可以认为流失的动量流强度与速度的平方成正比，又因为牵涉到两维运动，所以动量流强度需要用矢量表示。这样，从重力场流入跳伞员的动量流为：FG=mg。式中，g为重力加速度矢量。因为空气摩擦而流失的动量流为：Ip,out=kvv（Ip,out=kv2ev）。式中，ev表示运动方向的单位矢量，如图3所示。

图3 跳伞员的动量流图Fig. 3 Momentum flow diagram of a parachutist

根据动量连续性可确定：流入跳伞员的总动量流强度等于跳伞员的动量变化率，即

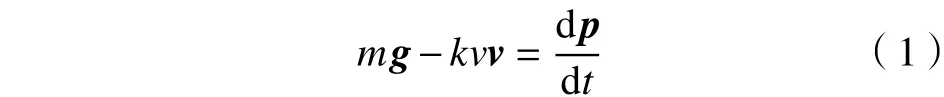
写成分量式（取飞机水平前进方向为x轴正方向，取向下为y轴正方向）：

由式（2）和式（3）所组成的方程组是有交叉项的一阶非线性齐次微分方程组，与用牛顿力学解题得到的方程组完全一样，数学上没有解析解。因此，文献[12]用计算机逐点计算描绘出速率与时间曲线，发现跳伞员在达到第一收尾速度之前会出现一个极小速率，但在文献[12]中并没有对这一现象进行更深层次的分析解释，因为用牛顿力学的原理难以对这一结果作出简单明了的解释，这里KPK力学体系可以有所作为。

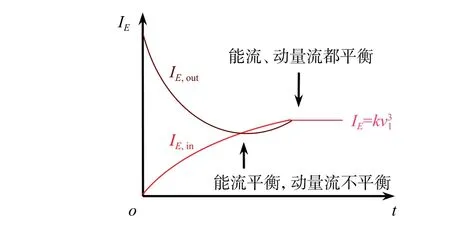
图4 跳伞员的能流变化曲线Fig. 4 Energy flow curve of the parachutist

图5 跳伞员的速率变化曲线Fig. 5 Rate curve of the parachutist

由于动量流是矢量，而流入与流出的动量又不在同一个方向，分量中又存在交叉项，因此仅利用动量流难以说出所以然来。但动量是能量载体，动量流动时携带着能量，而能量流可以用来确定速率的变化。这样，动量流结合能量流，可以对这一现象作出简单明了的解释。由重力场流入跳伞员的能量流强度为IE,in=v·FG=mgvy，而由摩擦流出跳伞员的能量流强度为kv3。如果飞机飞行速率大于跳伞员的第一收尾速度，那么跳伞员出舱后，流失的能量流强度就大于流入的能量流强度，因此跳伞员的速率在下降，一直到流入与流出的能量流强度相等。即：mgvy=kv3时，跳伞员的速率将达到一个极小值。尽管此时能量流维持平衡，但动量流并没有平衡（力没有平衡），在水平方向只有动量的流出而没有动量的流入。因此，尽管速率v没有变化，但是水平方向速度分量vx在减小而竖直方向的速度分量vy在增大，所以很快就会使能量流失去平衡，出现mgvy＞kv3的状况，即流入的能量流强度大于流出的能量流强度。因而，跳伞员的速率将会增加，直到水平方向速率为零，能量流再次取得平衡，mgv=kv3，同时动量流也取得平衡，mg=kv2，如图4所示，跳伞员才会达到第一收尾速度（约50 m/s）。可见在第一收尾速率之前会出现一个极小速率，此后跳伞员打开降落伞，而空气对降落伞的阻力非常大，意味着流出的动量流大幅增加，而流入的动量流却没有变化。因此，跳伞员的速率快速下降，流出的动量随着快速减少，直到能量流再次取得平衡而达到第二收尾速度（约4 m/s）为止，跳伞运动员跳出舱后直到落地的速率变化情况如图5所示。跳伞员以大约4 m/s较小的收尾速度飘向地面，这相当于从1 m高的窗台跳到地面的状况，大大降低了跳伞员从高空跳下落地时从身体流出的动量流，使跳伞员能安全落地。

4 结束语

把物体之间的相互作用看成是动量的流动，为力学现象的解释开辟了新的思路，也为力学问题的解决提供了新的方法。由于动量的流动可以与日常生活中熟悉的水流进行类比，这样一个系统的动量保持不变的条件就显而易见了；用动量流方法解力学问题不再进行受力分析，而是对系统进行动量流分析，物理图像更简洁；利用动量的连续性所列的方程方法，更贴近生活经验。以上例子说明卡尔斯鲁厄物理教程的力学体系简化了静力学系统的描述，用于解决动力学问题不但没有障碍，而且更有独到之处。