含阻挫和各向异性的反铁磁自旋链的键算符理论

卢蒙蒙，陈 斌

（上海理工大学 理学院，上海 200093）

近几十年来，低维磁系统是凝聚态物理中的一个重要领域。量子涨落在低维上的增强会导致很多新奇现象，如拉丁格液体行为和自旋皮尔斯相变。由于在铜基材料中发现了高温超导性[1]，方格点阵中最近邻的海森堡反铁磁体模型引起了理论界的广泛关注。对于一维铁磁体，Haldane[2]指出，整数自旋链的激发态具有有限的能隙，而半整数自旋链是无能隙的。半整数和整数自旋链的不同色散关系现象已经吸引了很多理论和实验研究者。S=1的自旋链是一个简单的例子（S为自旋），这一点已在S=1的磁性材料Ni（C2H8N2）2NO2（ClO4）中得到证实[3]。由于自旋轨道耦合，自旋Ni2+离子的各向异性效应不能被忽略。单粒子各向异性是高自旋的普遍现象。Sakai等[4]的研究表明，自旋为1/2的铁磁链的量子相变可能是单离子的各向异性引起的。通过平均场计算[5-6]也观察到了类似的相变。同时，Sachdev等[7]在二维量子反铁磁体中对自发二聚化相进行了广泛的研究。对于阻挫方晶格中的自发二聚化提出了自旋为1/2的键算符表示。此后，Wang等[8]引入了S=1的键算符理论方法来研究自旋为1的铁磁链和阶梯的磁化。Kumar等[9]应用此方法讨论了具有二聚化基态的一般性的反铁磁链。文献[10−11]使用键算符来处理亚铁磁链的二聚化效应。本文利用键算符的表示方法分别讨论了反铁磁自旋链中的单离子各向异性和阻挫。提出了具有阻挫和各向异性的S=1反铁磁自旋链的键算符平均场理论方法，得到了零温极限下的色散关系和有限温度下基于阻挫效应的能隙、磁化强度、静态磁化率和比热容数值。通过求解各向异性的参数讨论了阻挫效应下的物理性质。

1 键算符的表示方法

在实际材料中，阻挫是低维铁磁材料中普遍存在的现象。阻挫的自旋模型是一个基本模型，它与自旋皮尔斯材料密切相关[12]。由于自旋轨道相互作用的存在，S=1的自旋链的各向异性效应比S=1/2的自旋链的各向异性效应大得多。因此，考虑了S=1反铁磁海森堡自旋链的各向异性。现分别考虑阻挫和单离子各向异性对反铁磁自旋链的影响。哈密顿量

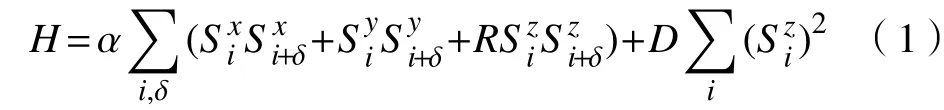
式中：α为阻挫参数；D为单离子各向异性参数；为i格点在x，y，z方向的自旋投影；R为各向异性因子，本文忽略不计；δ为铁磁链结构常数，在考虑阻挫的情况下，近似格点之间的距离相等，δ=0。

通过构造出自旋单态[13]，得到S=1的反铁磁自旋链的键算符

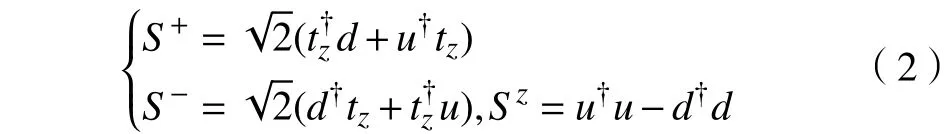
式中，tz，d，u是二聚体的耦合量子数。

式（2）中基态z方向上是玻色凝聚的，即为对算符取观测平均值。将键算符表示的升降算符代入哈密顿量，可以得到

式中，µ为依赖温度的化学势。

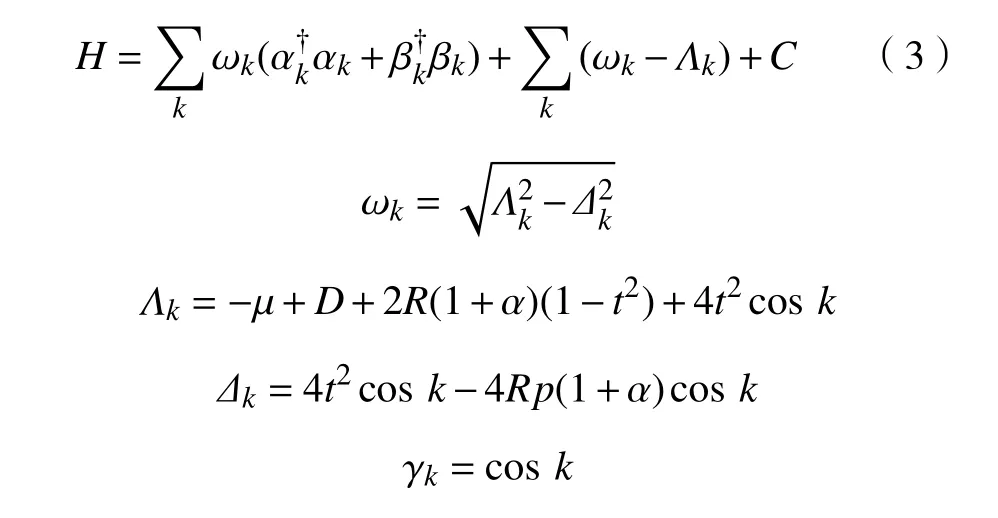
式中：γk为铁磁链的结构因子；C为常数。

然后得到格点的平均能量

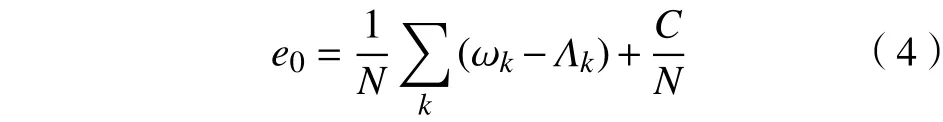
式中，N为铁磁链的格点总数。

同时得到参数的自恰方程组为

其中，β=1/(kBT)，kB=1，kB为玻尔兹曼常数，T为系统温度。

2 阻挫效应下的热力学性质

图1～4分别是在不考虑单粒子各项异性因子的情况下，考虑不同阻挫对激发谱、自由能、比热容和静态磁化率的影响。通过求解含有参数的自恰方程，得到了相应零温极限下的参数值。能谱的最小值在k=π处，得到能隙为0.7。这个数值下的系统与Haldane猜想下的系统是一致[14]。随着阻挫的增加，系统的能隙逐渐减小，在阻挫α=1.39时，能隙减小到0，这意味着相变可能由阻挫引起，相变临界点与Kato，Yamamoto，Hagiwara的数值结果是一致的[15-17]。采用不同的阻挫参数计算了自由能，如图2所示，随着温度的升高，自由能逐渐减小，同时，阻挫值越大，自由能相对越小。分析了不同阻挫下静态磁化率与温度的关系，当温度升高时，较小的阻挫值对应的静态磁化率增长比较慢，而在高温区域，静态磁化率增长相对比较快，阻挫越大，静态磁化率越大。在低温下，阻挫对磁化率的影响比较明显。研究发现，比热容在温度区域[0.1，0.5]呈线性增长，阻挫越大，比热容增长的速度越快。这表明S=1的反铁磁海森堡链在阻挫效应影响下会发生量子相变，这一现象已经在镍的含阻挫的铁磁系统中经实验证实[17]。

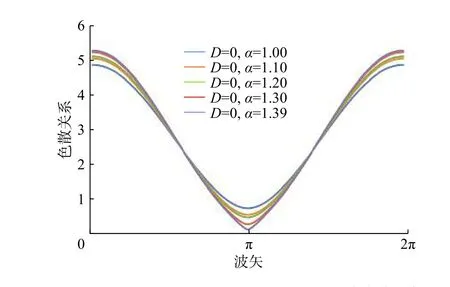
图1 D=0，α取值为1.0，1.1，1.2，1.39时的能谱图像Fig. 1 Energy spectrums with different bond alternation parameters α=1.0, 1.1, 1.2, 1.3, 1.39 at zero temperature,while D=0

图2 D=0，α取值为1.0，1.1，1.2，1.39时的自由能图像Fig. 2 Free energy diagrams with different bond alternation parameters α = 1.0, 1.1, 1.2, 1.3, 1.39 at finite temperature,while D=0

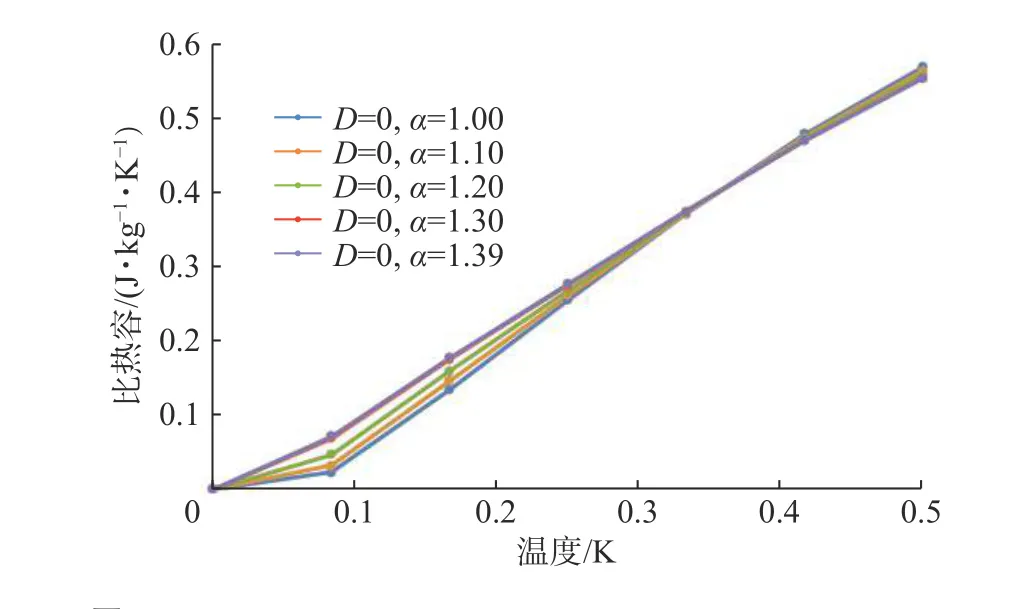
图3 D=0，α取值为1.0，1.1，1.2，1.39时的比热容图像Fig. 3 Specific heat capacity diagrams with different bond alternation parameters α=1.0, 1.1, 1.2, 1.3, 1.39 at finite temperature, while D=0

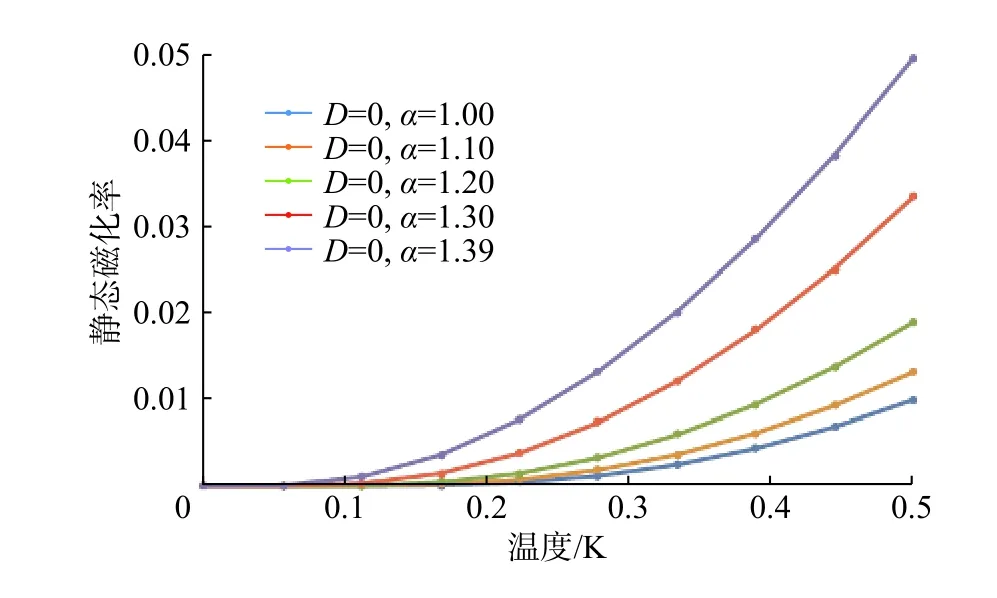
图4 D=0，α取值为1.0，1.1，1.2，1.39时磁化率图像Fig. 4 Uniform static susceptibility diagrams with different bond alternation parameters α = 1.0, 1.1, 1.2, 1.3, 1.39 at finite temperature, while D=0

3 各向异性影响下的热力学性质

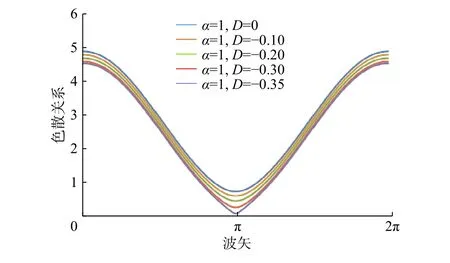
图5 α=1，D取值为0，−0.1，−0.2，−0.3，−0.35时的能谱图像Fig. 5 Energy spectrums with different anisotropy parameters D = 0, −0.1, −0.2, −0.3, −0.35 at zero temperature, while α=1

图5～8分别是在不考虑阻挫影响的情况下，不同的各项异性因子对低能激发谱、自由能、比热容和静态磁化率的影响。通过求解含有各向异性参数的自洽方程，得到的能谱如图5所示，当各向异性存在时，能谱较低。这个结果与阻挫效应的影响相比，能谱色散关系的变化很小。在D=−0.35时，系统能隙消失，这意味着各向异性也可以诱导量子相变。通过其他的数值方法，在D=−0.29也得到了这种相变[18-19]。同时得到各种热力学性质图像。当温度升高时，自由能降低得更快。各向异性较大的情况下，自由能相对较小，这个趋势与阻挫效应是相反的。在区域[0, 0.2]的静态磁化率几乎趋近于0。温度升高，静态磁化率趋于指数增长，各向异性越大，静态磁化率越大。同时从各向异性下比热容与温度的关系也可以看出，各向异性越大，比热容越大。在温度区域[0.1, 0.5]，比热容与温度呈线性增长。同时，键算符的各向异性量子相变与密度矩阵重整化群方法也很吻合[18]。

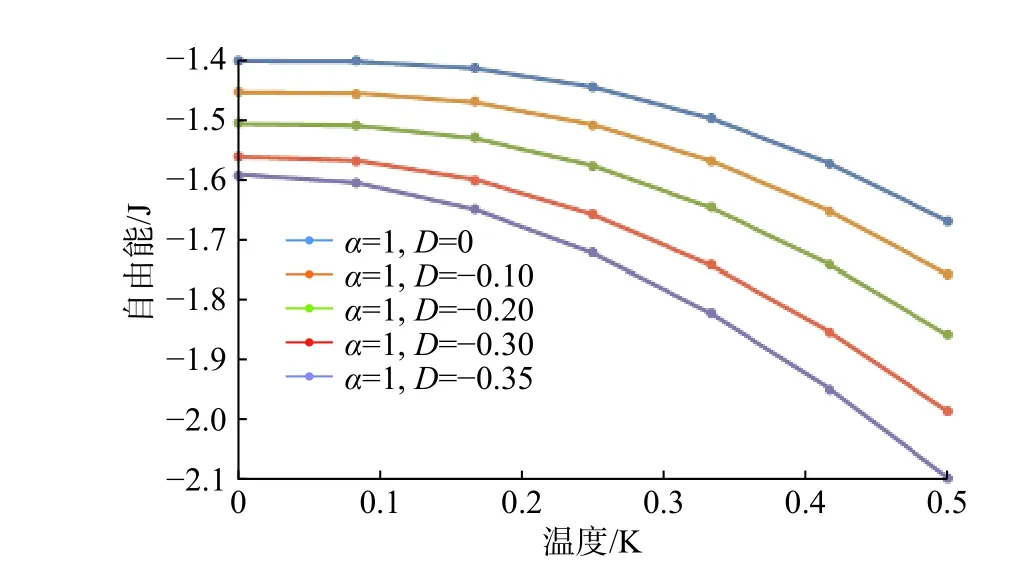
图6 α=1，D取值为0，−0.1，−0.2，−0.3，−0.35时的自由能图像Fig. 6 Free energy diagrams with different anisotropy parameters D = 0, −0.1, −0.2, −0.3, −0.35 at finite temperature, while α=1

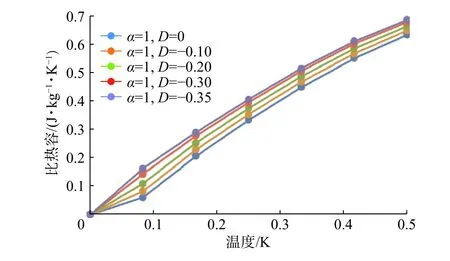
图7α=1，D取值为0，−0.1，−0.2，−0.3，−0.35时的比热容图像Fig. 7 Specific heat capacity diagrams with different anisotropy parameters D = 0, −0.1, −0.2, −0.3, −0.35 at finite temperature, while α=1

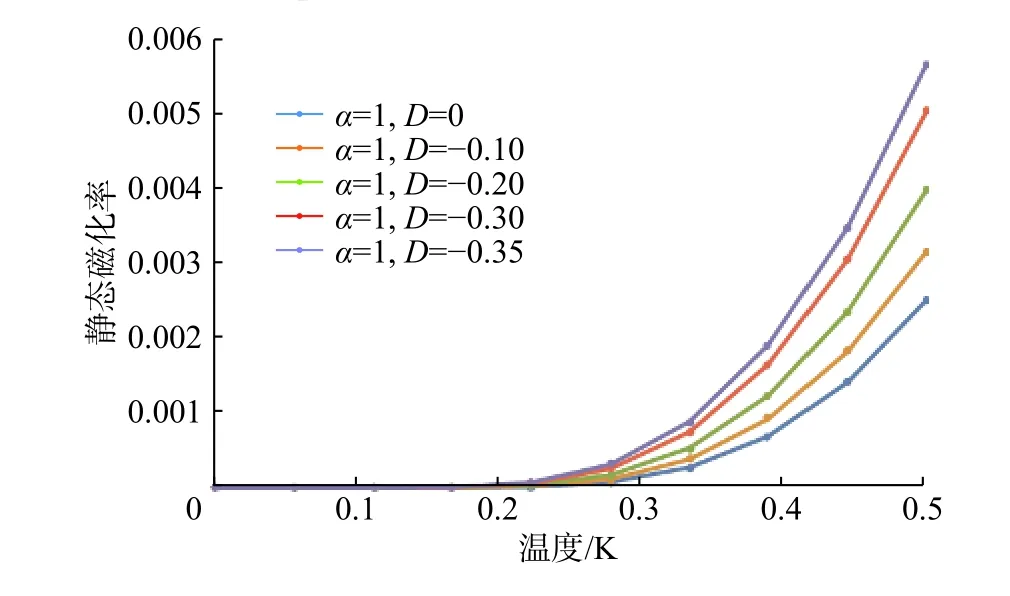
图8 α=1，D取值为0，−0.1，−0.2，−0.3，−0.35时的能磁化率图像Fig. 8 Uniform static susceptibility diagrams with different anisotropy parameters D = 0, −0.1, −0.2, −0.3, −0.35 at finite temperature, while α=1

4 结束语

通过键算符平均场近似的方法，讨论了阻挫和各向异性对S=1反铁磁海森堡链的影响。分析了阻挫和单粒子各向异性因子与能谱、自由能、静态磁化率和比热容的关系。阻挫效应引起的量子相变发生在 α=1.39处。通过求解各向异性的自洽方程，计算了系统的物理量。该系统能隙消失发生在D=−0.35处，这些结果与反铁磁自旋链上各向异性相变点D=−0.29的结果都是相一致的。因此，键算符方法也可以定性地描述阻挫和各向异性对S=1反铁磁海森堡链的影响。