基于卫星影像数据快速构建水动力水质模型研究
2021-01-27张诗豪徐宏亮刘宏宽周文婷
谭 鹏,张诗豪,徐宏亮,刘宏宽,彭 虹,周文婷
(1.中电建生态环境集团有限公司,深圳 518102;2.武汉大学水利水电学院,武汉 430072)
21世纪以来,随着中国经济的飞速发展,我国各大河流的水环境问题日益严峻[1-4],其中河道水动力水质模拟作为预测以及水污染防治的重要手段之一其作用越来越凸显重要性[5]。河道水下地形数据是进行水质模拟的基本条件,地形数据的质量直接影响水质模型模拟精度,地形处理不当甚至直接导致模拟计算的失败。当前,我国河流实时的数字化工作还相当不足,基本处于碎段化状态,难以适应高速经济发展带来的环境问题的需求,更不能满足当今我国对流域整体实施水环境精细化的管理目标。所以,在缺乏实测地形资料的地区如何获取满足模型运行所需要的河道水下地形数据,成为推广模型的重要限制条件。河道水下地形的测量,早期采用的方法主要有:光学定位方法、无线电定位方法以及深度测量方法[6]。目前采用比较多的方法有:遥感影像技术、水声定位、侧扫声呐、机载激光测量和无人船测量[7-12]。受测量条件和工作时间限制,水动力水质模型在缺乏实测水下地形资料时,一般会采用丰水期和枯水期水面线做概化处理。随着遥感影像技术的飞速发展,遥感影像分辨率越来越高,由10 m提高到3 m。这为没有条件进行水下地形实测的地区使用水动力水质模型提供了一种快速便捷的方法[13]。
本研究提出了一种基于Google Earth等遥感资料,利用普通克里金插值法[14]插值出河道地形[15],通过该插值地形构建水动力水质模型[16]。模型可以运用于地形相对较为缺乏的地区,且模拟结果能够达到一定的精度要求,可在资料缺乏区域,尤其在工程前期方案的比选中发挥重要的作用。
1 研究方法
1.1 Google Earth获取地形数据
对于没有河道边界及缺乏重点断面实测资料的河段,本次研究采用的是通过利用Google Earth等卫星地图工具,找到目的河道并勾取河道边界和重点断面,得到一系列边界散点和断面散点的经纬度坐标(WGS84坐标系)及对应的高程信息,并将各散点的经纬度坐标转换为模型计算所需的平面坐标。
利用Google Earth操作得到边界散点和断面散点经纬度的如图1,首先利用Google Earth找到本次研究的研究区域。随后,使用Google Earth中的添加路径与添加地标功能勾勒研究区域的边界线以及重点断面(如图2),采集的数据格式如图3所示,数据内容包括经纬度以及高程,最后导出边界点与断面散点的经纬度及高程。
转化公式如公式(1)~(3)所示:
X=(N+H)cosBcosL
(1)
Y=(N+H)cosBsinL
(2)
Z=[N+(1-e2)+H]sinB
(3)
式中:B为纬度,rad;L为经度,rad;H为大地高,m;e为地球的第一偏心率;N为地球面卯酉圈曲率半径。e和N可分别按如下公式求解:
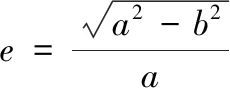
(4)
(5)
式中:a为地球长半轴,a=6 378 137.0 m;b为地球短半轴,b=6 356 752.314 2 m。
1.2 普通克里金插值
普通克里金插值法(Ordinary Kriging)是克里金插值法的一种,是一种依据协方差函数对随机过程进行插值的回归算法,该方法认为可依据区域上的一系列点X1,X2,…,Xn的观测值,采用一个线性组合来估计区域化变量在X0处的值,即:
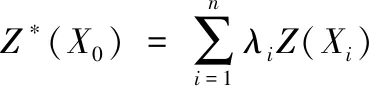
(6)
满足插值的无偏性和最优性,即要求:
E[Z(X0)-Z*(X0)]=0
(7)
D[Z(X0)-Z*(X0)]=min
(8)
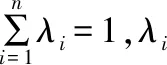
(9)
转化为λi求解的矩阵形式为:
(10)
其中Cij可通过变差函数γ(h)来确定,二维情况下,空间点P在X轴和Y轴上均有变化,可分别对x和y方向进行一维情况下的变差函数计算,即:
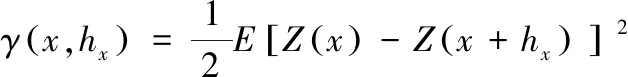
(11)
(12)
通常变差函数有球状模型、高斯模型、幂函数模型等,本研究采用球状模型:
(13)
式中:a为变程,即变量之间具有相关性的区域范围;h为滞后距;c为基台值,即变差函数在h大于变程时的值,为块金值c0和拱高cc之和。
块金值c0为变量纯随机性的部分,即在很短的距离内有较大的空间变异性,无论h多小,两个随机变量都不相关;拱高cc为观测值的变异幅度范围。变差函数、变程、滞后距、基台值、拱高、块金值之间的关系如图4所示。
1.3 二维水动力水质模型
本研究采用二维圣维南方程和二维污染物迁移转化方程模拟宽深比较大、断面变化较大的大型河道水动力学特征和水质迁移转化规律,即:
(1)二维圣维南方程包含连续方程和动量方程。
连续方程:
(14)
式中:H为微小水体的水深,m;u为x方向的流速,m/s;v为y方向的流速,m/s。
动量方程:
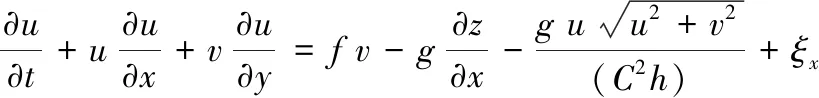
(15)
(16)
式中:g为重力加速度,m/s2;ρ为水体密度,kg/m3;C为谢才系数,m0.5/s;f为柯氏力常数,f=2Ωsinφ,φ为纬度,Ω为地转角速度;ξx、ξy分别为x、y方向上的涡动黏滞系数,m2/s。
边界条件:
上游边界条件或入流边界:
Q=Qin(t)
(17)
下游边界条件或出流边界:
z=zout(t)
(18)
初值条件:
φ=φin,t=0
(19)
式中:Q为流量,m3/s;z为水位,m;φ为Q,z中任何一个变量。
考虑对流、扩散、降解等项,二维水质模型基本方程如下:
(2)二维污染物迁移转化方程。
河流中的水质成分满足如下的守恒方程:
(20)
式中:ci为第i种物质的断面平均浓度,mg/L;Ex和Ey为河道的纵向和横向扩散系数,m2/s;SLi、SBi和SKi为第i种物质侧流入汇负Z荷、河道中源漏项,以及因水体水生态系统动力转换项,m·mg/(L·s)。
边界条件:
上游边界条件或入流边界:
C=Cin(t)
(21)
下游边界条件或出流边界:
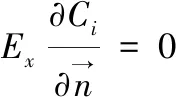
(22)
初值条件:
Ci=Cin,t=0
(23)
1.4 计算方法
首先,以河道研究可能涉及的最大水位,可以是历史高 洪水位或最高堤岸线,以此作为计算的外边界,通过网格生成程序生成模型计算的最大范围的计算网格。然后,依据圣维南方程,通过初始和边界条件,利用来流和下游水位及侧流入汇过程条件,根据横断面的水位变化,通过模型迭代计算,自动识别,判断出网格的干湿状态后,湿网格参与计算,干网格不参与计算,依次即可完成水动力水质模型中相应每个湿网格上的水位、流速和水质浓度的计算。
其中谷歌地球提取出来的高程,在校正插值后,构建出研究区域的水下地形,作为模型计算的边界条件。
2 研究区域
2.1 区域概况
研究河段为长江干流九江段,如图5所示,其上边界断面位于赛城闸上游4 km处,下边界断面为九江乌石矶粮库,长约20 km,宽约1.5~2.5 km。研究河段内有鹤问湖污水处理厂和老鹳塘污水处理厂两大污染源。
2.2 河道地形生成
依据上文所讲到的地形获取方法,根据九江河段的实际位置,使用Google Earth选取河道边界并沿河道均匀选取30个断面,得到河道边界和断面散点坐标,如图6所示。
利用获取的河道边界,绘制出平面二维正交网格,网格对应实际地形尺寸约为30 m×30 m,如图7所示。
依据河道边界散点以及选取的断面散点,结合网格结点坐标,利用普通克里金法插值计算每个网格结点处的高程信息,生成模型计算所需的地形标准文件。
如图8为根据遥感影像生成的河道地形与实测地形的对比图,图8(a)为根据遥感影像生成的地形,图8(b)为九江水文局2017年实测水下地形。从图8中可以看出,根据遥感影像生成的水下地形,尽管在趋势上与实测地形基本一致,但是在河道深泓线的表征方面还是不如实测地形连贯合理。
2.3 模型计算参数
本次研究以COD和NH3-N两种污染物为水质指标进行模拟计算,依据本河段水力条件,参考该河段相关研究成果,模型各参数取值范围如表1所示。

表1 水动力水质模型参数率定范围Tab.1 Calibration range of hydrodynamic water quality model parameters
鹤问湖污水处理厂和老鹳塘污水处理厂,排水规模分别为10和8 万t/d,两污水处理厂排污口处排放浓度及江段背景浓度如表2所示。
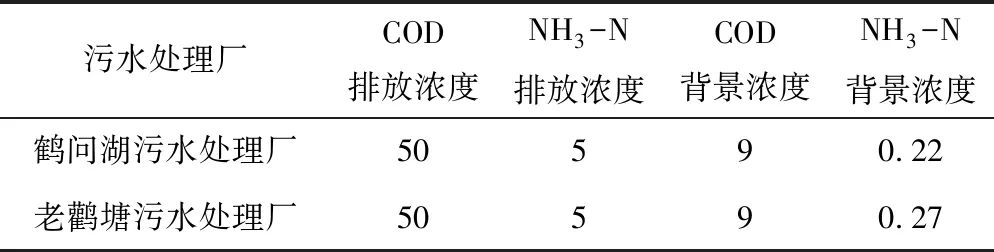
表2 污染物排放浓度及背景浓度 mg/L
2.4 结果对比
2.4.1 水动力对比
本次研究区域内,共有CS1、九江站、CS2 3个水文测验断面,如图9所示。其验证数据为九江水文局在2008年9月6日的水文测验实测水文资料。
本研究选取这3个断面的实测水位、流速进行模型验证。其中,CS1、九江站、CS2 3个水文测验断面平均水位验证结果及误差如表3所示,流速验证结果及误差如表4所示。
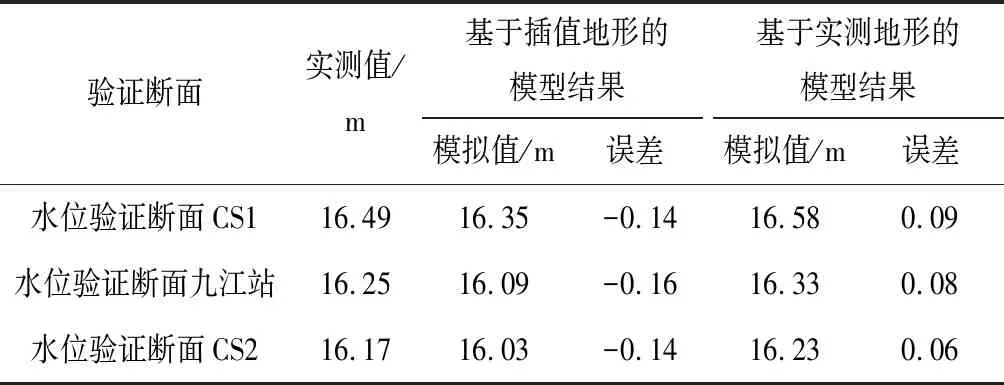
表3 两种地形条件下水位模拟结果误差统计表Tab.3 Statistics of water level simulation results under two terrain conditions
由表3和表4可以看出,基于插值地形的模型在绝大多实测点的相对误差值都比基于实测地形的模型要大,其中基于实测地形模型的相对误差都在10%以下,而本次研究所构建的基于插值地形的模型相对误差均在20%以下,两种地形所构建的模型都能够较好的模拟河道水动力规律。

表4 两种地形条件下模型流速模拟结果误差统计表Tab.4 Error statistics of simulation results of model velocity under two terrain conditions
2.4.2 水质对比
模型水质验证根据九江水文局2015年9月2日实测水质数据进行验证,选取研究河段内的抗洪广场、河西水厂、第三水厂(河东水厂)、乌石矶粮库为水质测验断面,如图10所示。
水质验证输入条件如表5所示。

表5 水质验证输入条件Tab.5 Input conditions for water quality verification
基于两种地形的模型在抗洪广场、河西水厂、第三水厂、乌石矶断面4个水质监测断面处的COD及NH3-N断面平均浓度模拟结果及误差如表6、7所示。
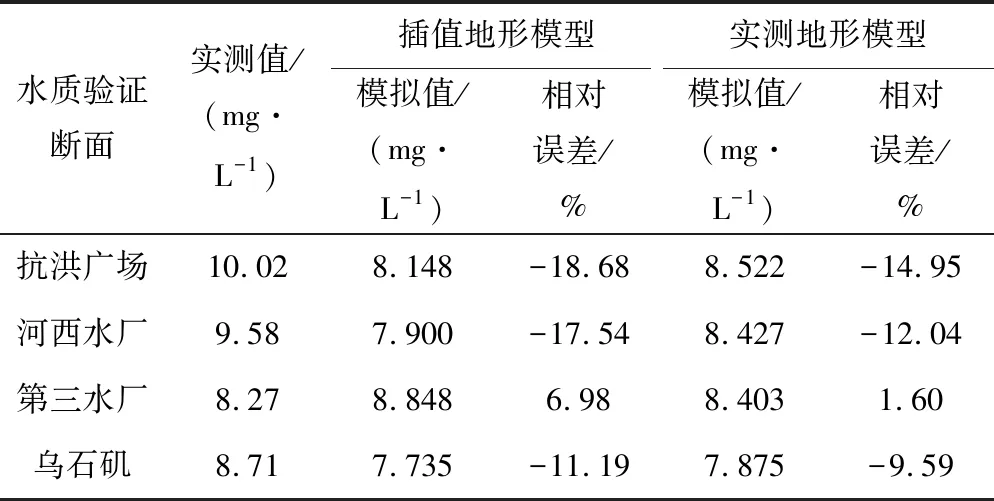
表6 COD浓度模拟结果误差统计表Tab.6 Error statistics of COD concentration simulation results
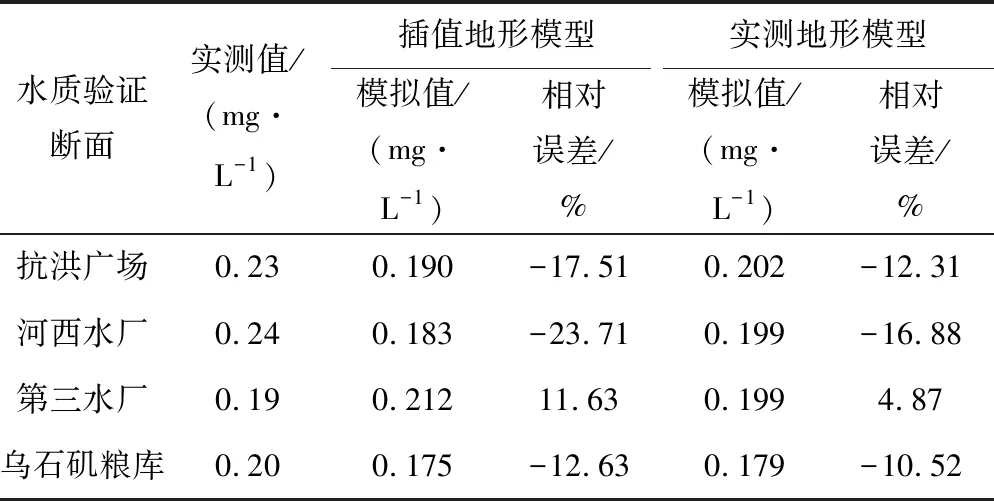
表7 NH3-N浓度模拟结果误差统计表Tab.7 Error statistics of NH3-N concentration simulation results
从表6和表7可知,本次研究基于插值地形模型在水质模拟方面,相对误差普遍大于基于实测地形的模型,插值地形的模型结果最大相对误差出现在河西水厂的NH3-N模拟上,达到了23.71%,小于30%;实测地形模型的最大相对误差同样出现在河西水厂的NH3-N模拟上,达到了16.88%,小于20%。
综合对比水动力模拟精度以及水质模拟精度,本次研究基于插值地形的模型模拟精度不如实测地形,但是其在验证断面处,水位模拟误差小于0.2 m,流速模拟相对误差小于20%,水质模拟相对误差小于30%,整体的模拟精度仍然能够满足实际需要。所以在一定精度范围内,本文基于插值地形的模型优于实测地形模型的地方在于,基于地形插值的模型能够用于缺少地形资料的地区。
3 结 论
本次研究通过二维圣维南方程、二维污染物迁移转化方程,利用遥感数据获取河道边界及断面地形,采用克里金插值法生成模型计算所需的地形标准文件,建立了水动力水质模型。经过验证,水动力模拟相对误差不超过20%,水质模拟相对误差不超过30%。
将本次研究所构建的基于地形插值模型与基于实测地形模型进行对比,两者使用相同的水文输入条件,区别在于二者的地形数据不同。结果表明,本次研究所构建的基于插值地形的模型水质模拟最大相对误差不超过30%,而基于实测地形模型的最大相对误差不超过20%,实测地形模型的模拟精度更大,但是在一定的精度范围内,都可满足不同实际的需要。下一步希望能够在更多的研究区域使用本方法构建水动力水质模型,从而多方面验证基于地形插值模型的精度。
由于我国河流数字化工作不足,大部分河流的地形资料还处于缺乏状态。本文提出的基于遥感影像数据快速构建水下地形进行水动力水质模拟,虽然在模拟精度上不能有好的效果,但是在为无资料地区的突发水污染预警上还是有一定应用实际意义,可以为污染物运移趋势提供预测,为污染事故防治提供指导。
特别值得说明的是,本次研究所使用的遥感影像数据来源于Google Earth,所以模拟精度和Google Earth提供的数据精度密切相关。实践者在使用时,请一定首先校核下数据精度是否在米级变化。我们相信,随着技术的发展,会有更多其他遥感影像能够提供精度更高的数据服务于水动力水质模型的构建,水质模型专业人士可以密切关注该领域的科技发展动态,以便更好地服务于水环境保护领域。
□
