爆破地震波传播过程中的多普勒效应研究❋

陈建龙

①中铁第一勘察设计院集团有限公司(陕西西安，710043)

②陕西省铁道及地下交通工程重点实验室(中铁一院)(陕西西安，710043)

引言

爆破施工过程中产生的爆破振动对保留岩体和附近建筑物均有不利的影响；因此，有必要对爆破振动的控制进行相关的研究。 而爆破振动主要是由介质中爆破地震波的传播而引起的。

爆源参数和岩体特性对爆破地震波传播均有很大的影响[1]，这就决定了爆破地震波在空间和时间上均具有随机性[2]。 同时，由于爆破振动频谱曲线的范围是连续的，说明其包含的频率也是连续的[3]。 尽管频谱分布连续，但其幅值却差异很大，而幅值大小的差异代表着该频率所携带能量的不同。 因此，爆破振动频率与爆破振动产生的破环效应具有密切的联系。 基于这种联系，为了进一步控制爆破振动及其产生的破环效应，有必要针对爆破振动频率进行研究。

爆破地震波是一种复杂的复合机械波。 而波在传播过程中存在着多普勒效应。 因此，在理论上，爆破地震波在传播过程中同样存在着多普勒效应[4]。

目前，国内外在地震研究领域对多普勒效应已有相关的研究和应用。 李启成等[5]利用多普勒效应的原理提出了地震作用下断层滑动速度的方法，并以四川汶川地震的余震为例验证了该方法的可行性。 刘瑞丰等[6]以汶川地震198 个全球地震站检测的数据为背景，研究得到地震波传播时，由于多普勒效应导致震源东北向的地震动有所加强，而西南方向有所减弱。 许力生等[7]以青海玉树地震为背景，通过地震波反演得到震源破裂模型，表明破裂过程产生的多普勒效应加重了地震的破环性。 施富强[8]基于对爆破振动频率的研究，成功实现利用多普勒效应进行频率控制，达到拆除爆破的目的。

上述研究从理论上指出地震波传播中存在多普勒效应的影响，但在爆破振动方面的应用研究较少，也没有对多普勒效应进行具体的试验研究论证，缺少其与振动频率之间关系的研究。

爆破振动具有随机性和复杂性。 因此，直接验证多普勒效应对爆破振动频率的影响较为困难。 但是，可以利用毫秒延时起爆条件下爆破振动频谱结构的特殊性来研究。 在毫秒延时起爆时，产生的爆破载荷可以等效看做是作用在岩体上的外界强迫激励[9]。 Blair[10]指出，毫秒延时起爆时，若相邻爆源的起爆时间均相差t，则得到的频谱曲线的峰值均出现在t -1及其整数倍处。 因此，可根据延时爆破情况下起爆间隔时间和产生的振动频率在数值上的这种特殊关联，通过合理设计起爆时间得到预期的爆破振动频率范围。

基于已有的研究，通过对爆破振动频谱的分析与计算，利用模态识别方法进行数据处理，结合数值模拟，研究爆破地震波传播中的多普勒效应及其对爆破振动频谱的影响。

1 毫秒延时起爆条件下的爆破振动频谱结构

1.1 毫秒延时爆破的振动频谱

毫秒延时爆破的振动频谱与间隔起爆时间具有相关性，具体公式推导如下。

单孔起爆的振动频谱由傅里叶变换[11]求得:

式中:f代表频率；un(t)为各炮孔的振动波形；~un(f)为第n个孔爆破振动信号的傅里叶变换；t为时间。

变换式(1)形式得

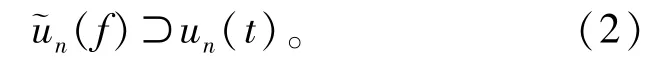
傅里叶变换的基本定理:

则多段爆破总振动的频域表达式为

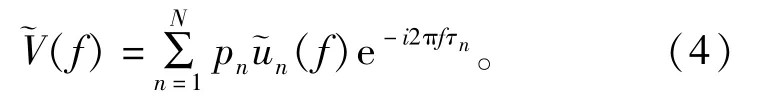
假定多孔起爆时其控制点位于爆破远区，则该点到各炮孔的距离可以看成是相等的(rn ＝r；hn ＝h)，且当各炮孔药量相等时(qn ＝q)，其爆破振动所得波形一样，均为v(t)，该波形的傅里叶变换假设为~v(f)，则式(4)可以化简为

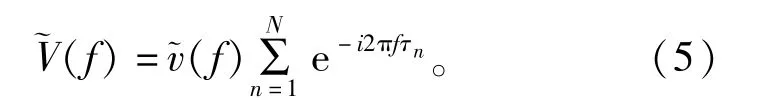
当各相邻炮孔为理想延时(无误差)起爆时，其微差延时间隔可认为是相等的，均为△τ，即τn ＝(n-1)△τ，则式(5)变为

设每个炮孔起爆产生的时程曲线v(t)的时间是ts，得到单个炮孔的功率谱密度ps(f)＝｜V(f)｜2/ts，则多段V(t)的总时间长tV ＝ts +(N -1)△τ，其总的功率谱密度为

令S(f)＝sin2(πfN△τ)/sin2(πf△τ)，功率谱因子S(f)是一个周期为(△τ)-1的周期函数，其自变量为f，当f ＝n/△τ(n∈Z +)时，函数S(f)最大。因此，若炮孔以时间差△τ依次起爆，由其产生的振动波形经过FFT 变换得到的振动频谱的峰值均出现在(△τ)-1及其整数倍处。

1.2 模态识别在爆破振动数据处理中的应用

模态识别方法包括频域法和时域法。 频域法需要对数据进行傅里叶变换，从而在频域范围识别参数；而时域法识别时，通常不需要激励载荷数据，只需对结构响应数据进行处理即可得到模态参数，而且对结构的自由响应和强迫振动均可以进行处理。

由于爆破载荷对岩体的作用是一种外界瞬态激励，一般其激励载荷大小很难直接获得，但可以很容易测得其爆破振动的响应数据；因此，可以利用模态识别的时域法来求得系统的模态参数，采用ARMA时序分析法[12]进行爆破振动数据的处理。 基于Matlab 程序，对爆破振动数据利用ARMA 法进行处理。 根据ARMA 法数据处理的要求，不仅需要监测计算测点的振动数据，同时还需要监测测点附近某参考点的数据，对测点和参考点的数据进行相关函数的运算，可以得到该测点的脉冲响应函数。 然后，以该响应函数为ARMA 法的输入数据进行模态参数识别。 ARMA 法作为时域法的一种，同样具有时域法不能消除噪声信号干扰的缺点。 因此，还需进一步对所得结果剔除噪声信号，提取有效信号。

2 毫秒延时爆破中的多普勒效应

2.1 爆破地震波传播中的多普勒效应

多普勒效应[13]是当振动波源与测点之间存在相对运动时，测点实际接收到的频率并不等于波源实际频率的现象。

根据多普勒效应的定义，进行毫秒延时爆破作业时，爆源依次起爆，而监测点一般是静止不动的。因此，爆破过程中会有多普勒效应的现象。 同样在该过程中，测点是静止的，而爆源是相对测点移动的。 具体原理如图1 所示。

图1 波源做相对运动Fig.1 Relative motion of wave sources

如图1 所示，假设观测点到波源连线和波源运动矢量方向之间的夹角为α，该波源自身波速为v，波的频率为f0。 在波源相对于测点以速度vA运动而测点静止不动时，该测点接受到的频率f为:

对式(10)进一步分析，当观测点到波源连线和波源运动矢量方向之间的夹角α ＜90°时，cosα ＞0，则f ＞f0，即测点接收到的频率f大于波源的固有频率f0；当夹角α ＝90°时，cosα ＝0，则f ＝f0，即测点接收到的频率f等于波源自身的的固有频率f0；当夹角90° ＜α ＜180°时，cosα ＜0，则f ＜f0，即测点接收到的频率f小于波源自身的的固有频率f0。

根据多普勒效应原理，波传播时测点接收的频率会因爆源与测点间的相对运动而产生变化。 爆破地震波传播过程中同样会存在由多普勒效应导致的频率偏移。 由于爆破地震波包含的成分是非常复杂且丰富的，这种情况下很难明显地发现多普勒效应导致频率偏移的规律。 但是，在毫秒差起爆情况下，爆破振动频率表现出一定的规律性，即当炮孔起爆间隔时间为△τ时，其爆破振动频谱曲线的峰值均大约相隔(△τ)-1。 因此，可利用该规律进行多普勒效应导致爆破振动频率偏移的验证和分析。 下面利用数值模拟进行验证。

2.2 多普勒效应的数值模拟验证

为验证毫秒延时爆破过程中存在着多普勒效应，并分析其对爆破振动频率的影响，建立ANSYS模型，如图2 所示。 利用其动力有限元分析模块LS-DYNA 进行计算处理。 图2 模型尺寸为50 m ×15 m×5 m，炮孔直径取0.6 m，各炮孔间距10 m。爆破载荷用理想的三角形载荷模型来代替，3 个炮孔以25 ms 的间隔时间从左往右依次起爆。 为了使爆破地震波传播时不出现波的反射和折射现象，在模型周围设置无反射边界。

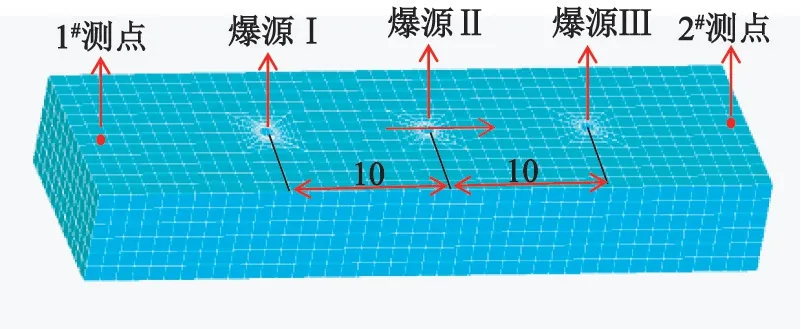
图2 ANSYS 模型示意图Fig.2 Schematic diagram of ANSYS model

岩体采用弹塑性模型材料，在ANSYS 中通过设置关键词Mat_Plastic_Kinematic 来实现，相关材料参数如表1 所示。 在爆源轴线两侧布置2 个监测点，记录其振动数据。

表1 模型材料参数Tab.1 Model material parameters

上述模型计算完成后，输出所布置测点处的振动数据，结果如图3 所示。

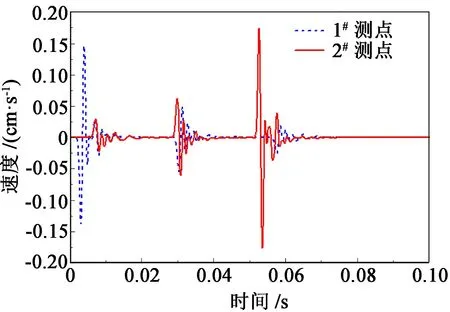
图3 ANSYS 模型各测点的爆速曲线Fig.3 Detonation velocity curves of each measuring point in ANSYS model

从图3 可以看出，两测点波形均有3 个明显峰值；并且，随爆源Ⅰ向爆源Ⅲ方向依次起爆。 由于炮孔逐渐靠近2＃测点而逐渐远离1＃测点，因此，靠近爆源Ⅰ的左侧1＃测点的各峰值依次减小，而靠近爆源Ⅲ的右侧2＃测点的各峰值依次增大。 输出图3曲线的振动数据，并用ARMA 法进行处理，识别得到爆破振动频率结果，如表2 所示。

表2 各测点的振动频率Tab.2 Vibration frequency at each measuring pointHz

同时，利用传统FFT 变换处理数据，求得1＃测点和2＃测点的频谱曲线，如图4 所示。

图4 各测点的频谱曲线Fig.4 Spectrum curves at each measuring point

1＃测点的谐振频率约为35 Hz 的整数倍，而2＃测点的谐振频率约为45 Hz 的整数倍。 这证明了当炮孔以△τ时间差依次起爆时，由其得到的振动频谱曲线的峰值均出现在某一数值的整数倍处。 本次数值模拟采用的相邻爆源间的延迟起爆时间间隔都为0.025 m，其谐振频率应为1/0.025 ＝40 Hz 的整数倍。 但计算结果表明，炮孔一侧大于40 Hz，而另一侧小于40 Hz。 这是由于爆破地震波在传播时存在的多普勒效应引起了两侧爆破谐振频率的偏移。具体分析可知，爆源从左向右依次起爆，逐渐靠近位于爆区右侧的2＃测点，即爆源运动方向与爆源-测点连线方向所成的夹角α ＜90°时，cosα ＞0，则f ＞f0，即实际传播到测点的频率f大于波源自身的频率f0；反之，爆源逐渐远离1＃测点，则实际传播到测点的频率f小于波源自身的频率f0。

2.3 多普勒效应引起的爆破振动频率偏移分析

1＃测点和2＃测点位于炮孔起爆方向上。 其中，1＃测点的谐振频率为35 Hz 的整数倍，而2＃测点的谐振频率为45 Hz 的整数倍；前者小于40 Hz，而后者大于40 Hz。 对结果按照式(10)进行计算。 其中，1＃测点α ＝180°，2＃测点α ＝0°，爆源相对于测点的运动速度vA＝10/0.025 ＝400 m/s，爆源自身的频率f0＝40 Hz，假设爆破弹性纵波在介质中的传播速度v ＝3 300 m/s。 由此求得1＃测点和2＃测点的频率值与数值计算得到的值几乎完全吻合。 如图5 所示。

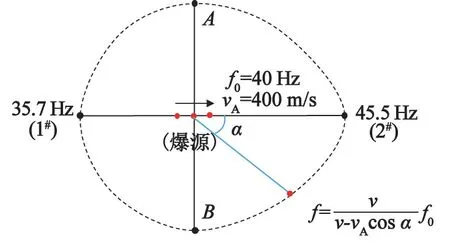
图5 多普勒效应频移机制Fig.5 Frequency shift diagram in Doppler effect

因此，多段延时爆破振动的频谱一方面包括爆源自身延时起爆的频率，另一方面还包括因爆源相对测点运动而产生的频率偏移；毫秒延时起爆情况下爆源周围任意方向处的频率可通过多普勒原理的公式计算得到。 特殊地，对于垂直于炮孔轴线(图5中AB线)的两侧，α ＝90°，得到f ＝f0，即该处没有多普勒效应产生的频率偏移。

3 讨论

针对上述计算结果，从时间角度来看，当不考虑孔间延迟，即假定炮孔均在空间同一位置处，则其爆破振动频率为1/0.025 ＝40 Hz；而实际情况下，各炮孔间存在一定距离，爆破地震波在该段距离传播需要时间，因此，实际到达测点的时间间隔不仅包括炮孔自身0.025 m 的时间，还包括孔间传播产生的时间，具体为炮孔间距与波速的比，即10/3 300 ＝0.003 s。 1＃测点实际接收到振动信号的时间间隔为0.028 m，而2＃测点则为0.022 s，计算得到其频率与多普勒效应原理的计算结果一致。 因此，在不考虑爆源相对运动产生多普勒效应的情况下，各炮孔以t时间差依次起爆时，由其得到的振动频谱曲线的峰值均出现在t -1及其整数倍处。 而在考虑爆源相对测点运动引起多普勒效应情况下，其振动频谱曲线的峰值均出现在(t ± t1)-1及其整数倍处。其中，t1为孔间传播延时。

4 结论

通过对爆破振动传播过程中的多普勒效应的分析与研究，主要得到以下几点结论:

1)爆破地震波在传播过程中存在多普勒效应；

2)多段延时爆破振动的频谱一方面包括爆源自身延时起爆的频率，另一方面还包括因爆源相对测点运动引起多普勒效应而产生的频率偏移；

3)在爆源不同方向处，多普勒效应对爆破振动频率的偏移量大小也不同，与起爆方向同向一侧最大，反向一侧最小。