埋地输油管道对爆破振动的动力响应❋
2021-01-27高文乐李坤鹏段耀奎张春玉
高文乐 李坤鹏 段耀奎 冯 娜 张春玉
①山东科技大学土木工程与建筑学院(山东青岛,266590)
②济南鲁威科安振动检测有限公司(山东济南,250000)
引言
目前,管道运输在石油运输与调配中起到重要作用,覆盖全国的油气管网格局已经形成[1]。 在管道运输过程中,难免会遇到爆破作业。 爆破施工产生的爆破振动会对邻近埋地输油管道产生影响,甚至导致管道破裂,造成资源浪费,同时存在很大的安全隐患。 国内外制定的管道上方地表振速控制标准差别较大[2],爆破振动对管道的影响无法得到准确计算。 因此,可以运用数值模拟分析爆破振动对埋地管道的影响。 王树江[3]运用ANSYS/LS-DYNA 有限元软件建立了包含炸药、岩土体、埋地管道的管土耦合模型,通过爆破动力载荷数值模拟,分析管土耦合模型受爆破动载荷的动力响应。郝郁清[4]运用有限元软件建立管土三维数值模型,分析不同装药量及爆心距工况下埋地燃气管道、地表土体对爆破振动的动力响应。 黄雄[5]运用LS-DYNA 软件建立三维有限元模型,证明管道迎爆面中心单元应变峰值和振速峰值均随着药量的增加而增加,随着爆心距的增加而减小。 舒懿东[6]建立三维动力有限元计算模型,分析爆破振动下埋地天然气管道的管径、壁厚和埋深等参数对管道及地表振动特征和管道Von-Mises 应力的影响规律。 张玉琦等[7]分析了爆破地震载荷作用下埋地管道的动力响应特征,研究了管道振动速度及动态应变分布特征。
上述文献均研究了爆破振动对邻近埋地管道的影响,但是仅停留在对埋地管道单个方向的分析。由此,结合邻近埋地输油管道的某港区疏港大道土石方爆破工程进行研究,对埋地管道的迎爆面、背爆面、管顶和管底4 个面进行分析,总结不同方向结构面应力分布规律。
1 有限元模型
1.1 计算模型建立
碎土石层厚度为2.0 m,两管道平均埋深为2.8 m,相距0.7 m,管径1 020.0 mm,壁厚12.7 mm。 爆源与管道水平距离46.0 m,竖直距离3.5 m,外侧管道中心距离模型另一端外边界4.0 m。
采用ANSYS/LS-DYNA 有限元软件建立模型,进行数值模拟。 由于管道内的液体流动压力远小于管道所承受的强度,建模时不考虑管道内部液体和动压力的影响。 根据对称关系,建立1/2 模型进行简化计算,参数单位采用cm-g-μs。 令重力方向为Y轴负方向,垂直于管道长度方向为X轴正方向,平行于管道方向为Z轴方向。
具体位置及模型尺寸见图1 所示。
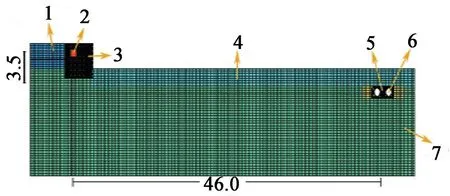
图1 模型尺寸示意图(单位:m)Fig.1 Model size diagram(unit:m)
在模型顶部炸药周围建立空气域,使得炸药爆炸后的能量在流体单元中流动,不存在单元的畸变问题。 基于管道实际埋地敷设施工中会在底部铺设垫层的情况,在模型最底部岩层和管道之间设置20 cm 厚的土层来模拟实际情况。 模型截面如图2 所示。
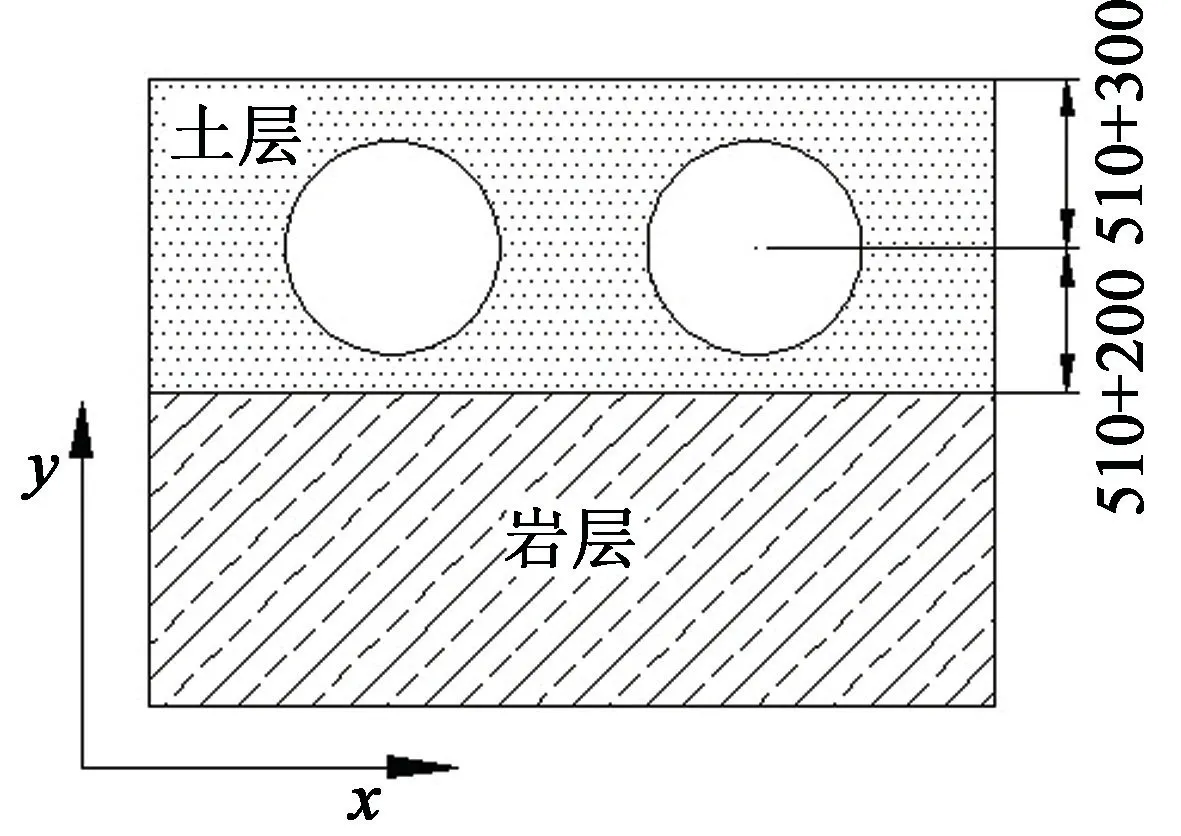
图2 管道模型截面图(单位:mm)Fig.2 Section of pipe model(unit:mm)
根据所研究问题特性,采用多物质流固耦合算法,即将炸药、空气等物质与固体结构的相互作用进行耦合计算[8]。
建模时,对流体材料(炸药及空气域)采用ALE算法,对固体材料(其他结构)采用Lagrange算法。在管道与土体接触处、炸药与被爆岩石接触处对网格进行加密,以保证计算的精度。 网格划分情况如图3 所示。
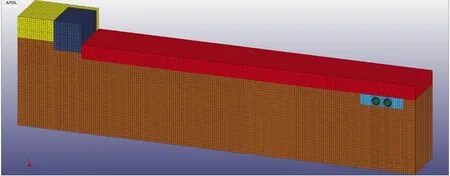
图3 模型网格划分示意图Fig.3 Schematic diagram of model grid division
1.2 材料本构模型及参数
1.2.1 岩石本构模型及相关参数
被爆岩石为弱风化白云质灰岩,采用*Mat_Plastic_Kinematic 弹塑性材料模型[9],主要参数如表1 所示。
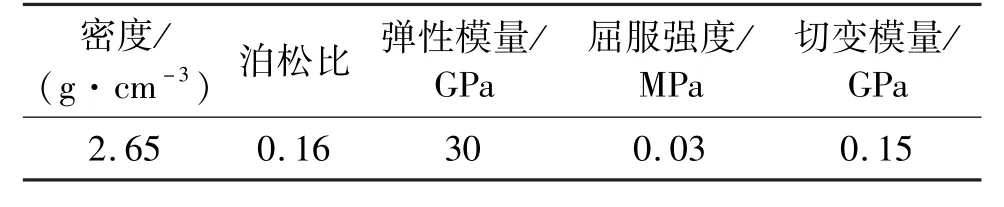
表1 岩体的相关力学参数Tab.1 Relevant mechanical parameters of rock mass
底部石灰岩采用HJC 模型(*Mat_Johnson_Holmquist_Concrete)[10-11],本构参数见表2。
1.2.2 土体本构模型及相关参数
土层采用*Mat_Drucker_Prager 材料模型,主要的物理力学参数见表3。
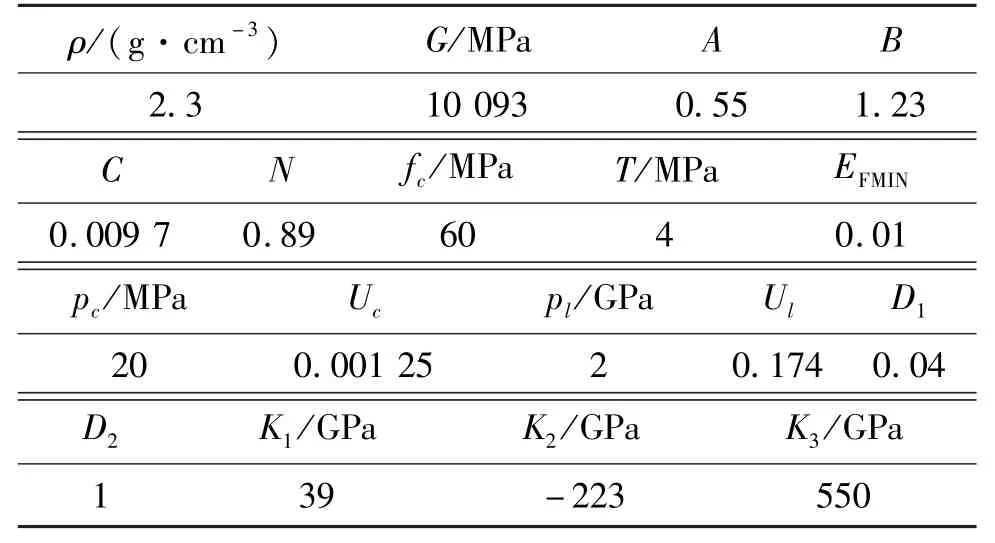
表2 石灰岩的HJC 模型参数Tab.2 Parameters of HJC model for limestone
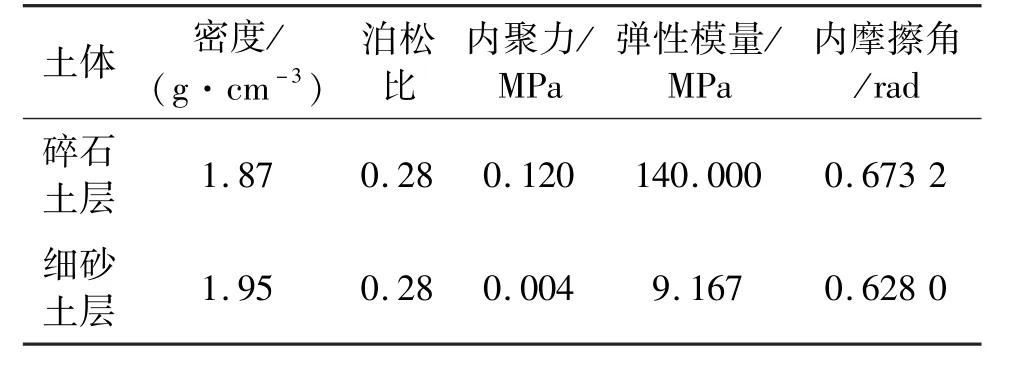
表3 土体的相关力学参数Tab.3 Relevant mechanical parameters of the soil
1.2.3 炸药本构模型及相关参数
炸药采用2#岩石乳化炸药、*Mat_High_Explosive_Burn 模型[9],材料的主要参数见表4。 采用JWL 状态方程模拟炸药爆轰产物的压力与体积的关系。
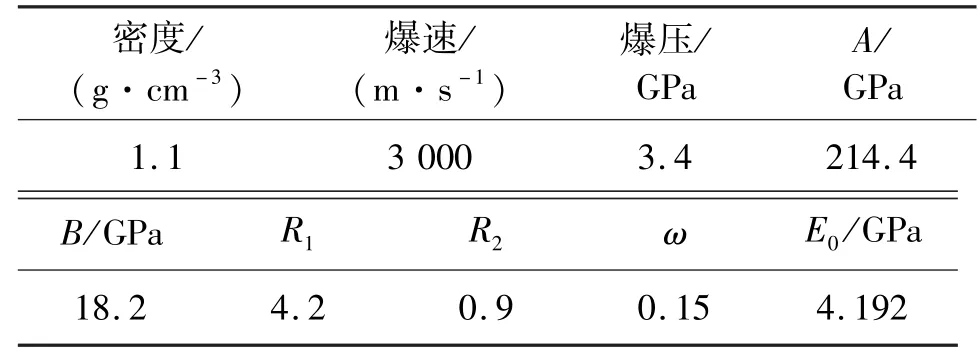
表4 炸药材料参数Tab.4 Material parameters of explosives
1.2.4 管道本构模型及相关参数
管道为X70 钢管,采用*Mat_Plastic_Kinematic弹塑性材料模型,服从Von-Mises 屈服准则,管道主要的参数[12]见表5。
1.2.5 空气本构模型及相关参数
空气采用*Mat_Null 材料模型和线性多项式状态方程*Eos_Linear_Polynomial 描述[13],在状态方程计算过程中不考虑偏应力。 力学参数见表6。
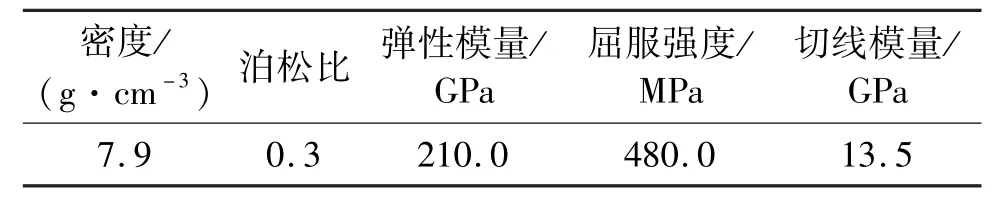
表5 管道的相关力学参数Tab.5 Relevant mechanical parameters of pipeline

表6 空气的相关力学参数Tab.6 Relevant mechanical parameters of air
2 数值模拟准确性验证
根据工程实例建立数值计算模型,取管道正上方与爆源水平距离46 m 的测点1#和61 m 的测点2#,其实测的地表峰值振速见表7。 选取模型中与测点1#相近位置处管道上方的地表的振速,其结果如图4 所示。
将现场监测数据与本次数值模拟结果进行比较分析可以发现,爆破振动现场测点1#的X方向、Y方向、Z方向峰值振速分别为0.82、0.74、0.64 cm/s,模拟计算结果的X方向、Y方向、Z方向峰值振速分别为0.78、0.63、0.59 cm/s,最大绝对误差为0.10 cm/s,相对误差为13. 5%,远低于30. 0%[14]。 因此,本次数值模拟是准确的,计算模型可以较好地模拟出现场的实际情况。

表7 爆破振动监测数据Tab.7 Monitoring data of blasting vibration
3 埋地管道应力分析
埋地输油管道计算时程内的应力云图见图5。
由图5可知,t=0 ms时刻炸药起爆,产生的冲击波从爆源中心向外传播,在5 ms后爆破地震波传到管道表面,随后应力波从中间沿管道轴向传播。传播过程中,管道面对爆心的迎爆面上的应力状态最先开始发生改变,应力值开始增大,且比管道其他位置处的应力都大;随着时间的流逝,管道上的应力先增大至最大,随后减小。
埋地输油管道不同位置处受爆破载荷的冲击和周围土体的作用不同,其动力响应也不同。 取左侧埋地输油管道横截面方向上A、B、C、D4 个位置来研究埋地输油管道的爆破振动响应规律。 管道截面取点位置见图6。 其中,A处位于迎爆面;B、D两处分别为管顶和管底;C处与A处相对,位于背爆面。
管道横截面4 个位置处有效应力随时间变化曲线见图7。
由图7 可知,爆破载荷作用下,管道近爆面(A处)的有效应力为1.46 MPa,管顶(B处)有效应力为0.77 MPa,管道背爆面(C处)有效应力为1.06 MPa,管底(D处)有效应力为0.84 MPa。 其中,A处有效应力最大,比C处有效应力高37.74%,比B、D处分别高89.61%、73.81%。C处有效应力比B、D处高37.66%、26.19%。
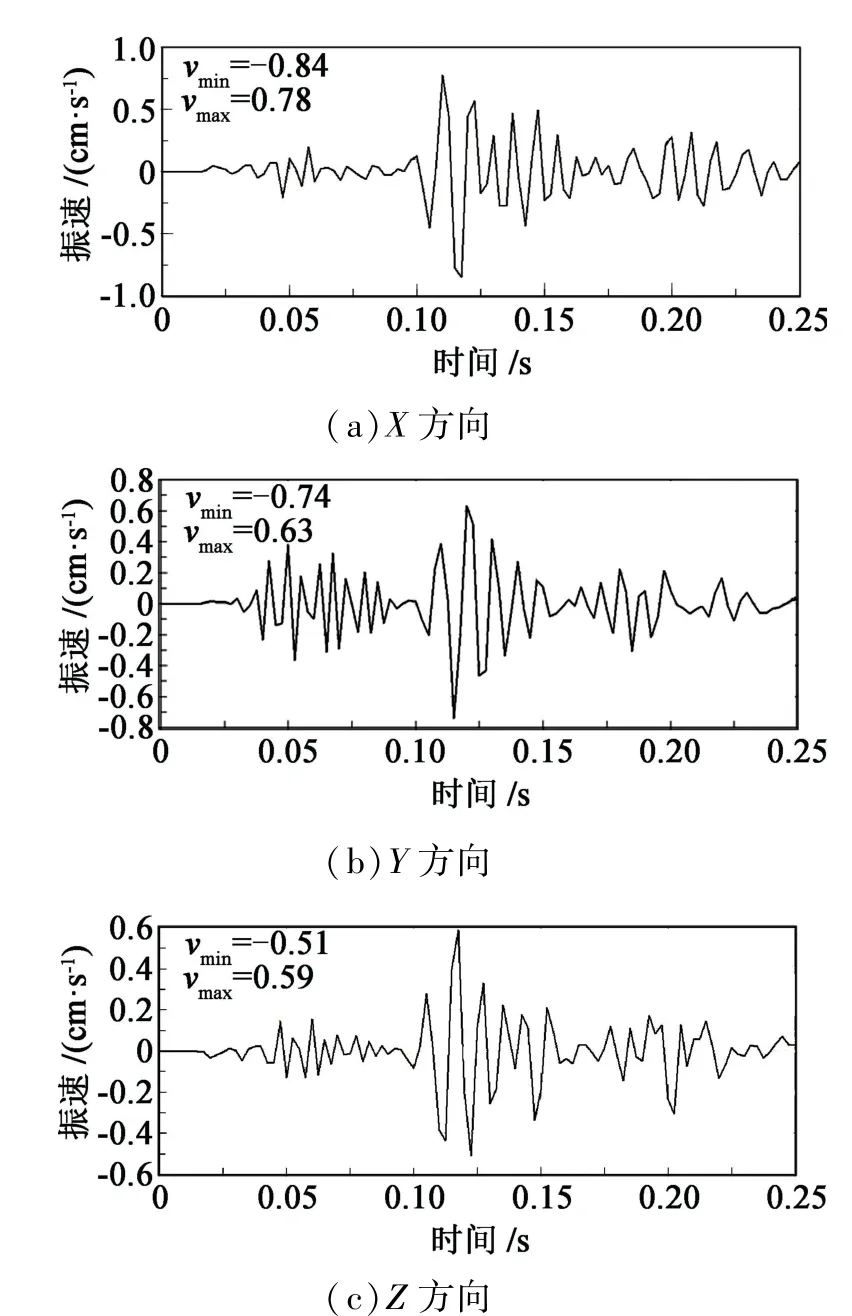
图4 模拟测点的振动速度波形图Fig.4 Vibration velocity waveform of simulated measuring points
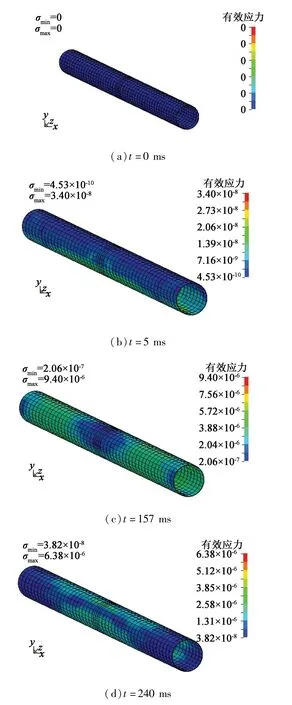
图5 埋地管道各时刻应力云图Fig.5 Stress nephogram of buried pipeline at each moment
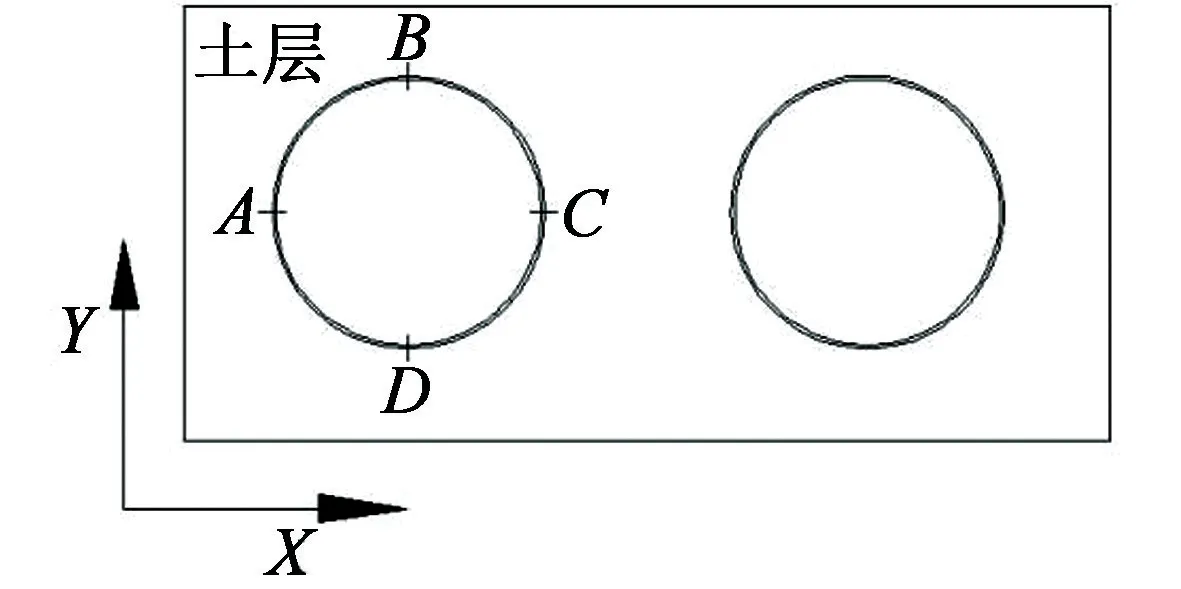
图6 管道截面取点位置Fig.6 Location of measuring points at the pipeline section
由以上分析可得:在爆破过程中,迎爆面的有效应力迅速增大至最大,之后开始衰减至0.1 ~0.4 MPa 范围内。 在爆破振动作用下,迎爆面和背爆面受到的应力远远高于管顶、管底的受力,且迎爆面的有效应力要大于背爆面,说明迎爆面是最容易发生变形的。 管顶和管底位于管道的中轴面上,受到的应力较小,变形也较小。 背爆面有效应力比管顶和管底的有效应力高,是由于当地震波经过左侧管道传递至右侧埋地管道时,右侧管道的波阻抗与土体不同,会在右侧管道处发生反射与折射,还会受到管道直径和壁厚的影响。
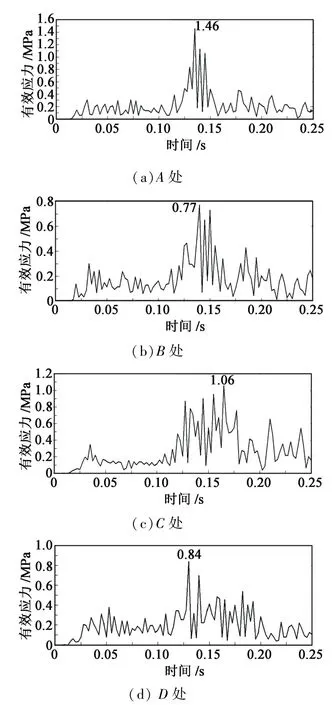
图7 有效应力曲线Fig.7 Effective stress curves
4 结论
1)通过ANSYS/LS-DYNA 流固耦合的方法模拟爆破过程,结果表明:基于流固耦合方法模拟得到的爆破振动速度与现场实测结果基本一致。 因此,在实际工程中可以采用流固耦合方法进行数值模拟,研究爆破振动对埋地输油管道影响的相关问题。
2)在爆破振动作用下,迎爆面和背爆面所受应力远高于管顶、管底所受应力,且迎爆面有效应力要大于背爆面,表明迎爆面是最容易发生变形的。 管顶和管底位于管道的中轴面上,受到的应力值较小,变形也较小。 当爆破地震波经过左侧管道传递至右侧埋地管道时,右侧管道的波阻抗与土体不同,爆破地震波会在右侧管道处发生反射与折射,反作用于左侧管道背爆面,使得背爆面应力比管顶和管底的应力大。
