基于多阶增量预测Exp-Golomb算法的冲击波数据压缩

2021-01-26童鸽徐悦王啸

长春理工大学学报（自然科学版） 2021年1期

童鸽，徐悦，王啸

（长春理工大学电子信息工程学院，长春 130022）

火炮、火箭炮和导弹等武器在发射时所形成的高温、高压、高速流场对操作人员、武器装备及周围环境等构成了严重危害，其中影响最大的因素之一就是冲击波［1］，冲击波的测试及冲击波场的描绘对于武器参数等的评定至关重要［2-4］。传统的冲击波测试系统主要可分为引线式测试系统和存储式测试系统［5］，其中前者布线繁杂，后者不可实时对数据进行观测［6］，然而无线冲击波测试系统则克服了传统测试系统的这两种缺点。但无线传输面临的最大问题是传输速率有限，目前常用的高速无线传输方式主要为802.11 ac/ax协议下的WiFi，但其有效传输速率仅达433/600 Mbit/s，若以Endevco的8510系列传感器作为冲击波的测量传感器，当测试系统的采样率高达2 MSa/s，采样精度为16位时，单一测试节点的数据产生速率高达32 Mbit/s，若要对冲击波场进行描绘，需要将数十个甚至上百个测试节点的数据同时进行上传，当同时上传节点数较多的时候，就会导致较大数据量与无线传输速率之间产生矛盾，进而导致系统实时性较差，因此有必要对信号进行压缩。

针对冲击波数据的压缩，张威峰等人［7］采用负延迟分区域存储的方式来减少随机瞬态信号高速采样中出现的大量冗余数据。王啸等人［8］采用频域分布比例门限法准确区分瞬态和非瞬态数据段，并且详细讨论了二分法和线性法在瞬态数据压缩上的压缩效果，以及数据的不同采样及恢复方法。上述方法对原始信号所采取的压缩方式为有损压缩，可能出现必要信息的丢失。因此，本文根据冲击波的突发性特征，采用时域门限判别法将冲击波数据分为瞬态数据段及非瞬态数据段，运用增量预测Exp-Golomb算法对冲击波数据进行压缩，并且根据瞬态信号随时间推移幅值变化趋于平缓的特性，提出多阶增量预测的改进算法。改进算法压缩率较原算法得到了较大提升，且克服了前人在瞬态数据部分压缩率较小的缺点。

1 冲击波信号的特征及识别方法

本文针对冲击波信号的特征，将其分为瞬态及非瞬态部分，并对不同部分采取不同的压缩策略。本章节首先阐述冲击波信号的特征，然后根据其特点，采用时域门限判别法区分瞬态及非瞬态信号。

1.1 冲击波信号的特征

冲击波信号属于典型的非平稳随机信号，其频谱范围约为0.3～100 kHz，具有突变快、上升沿陡峭以及超压峰值高等特点［9］。冲击波的压力值自其到达测试节点之后随时间的变化规律可由式（1）来表示［8］：

式中，ΔP为超压峰值；T+为正压作用时间；b为衰减系数，通常为1。其中ΔP的计算公式为国防工程设计规范（草案）中超压峰值计算公式：

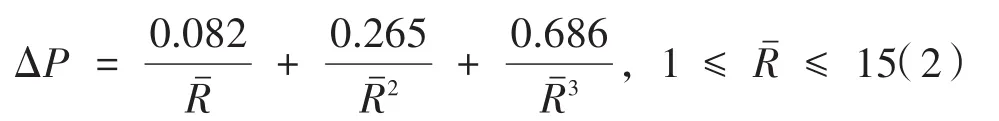
其中，冲击波比例距离算子Rˉ及正压作用时间T+的计算公式如下：

式中，r为测试节点到爆炸点的距离，单位m；ω为爆炸物的TNT当量，单位kg。

例如，取5 kg爆炸物的TNT当量，在距离爆炸点10 m处的地点，根据式（1）计算出的冲击波的压力值随时间的变化规律如图1所示。

图1 理想冲击波波形图

从图1可以看出，该次数值模拟从0.03 s处开始出现瞬态信号，0.06 s处幅值渐变为0；下图为某次爆炸试验中某支50 psi量程压力传感器所测得的实际冲击波波形。

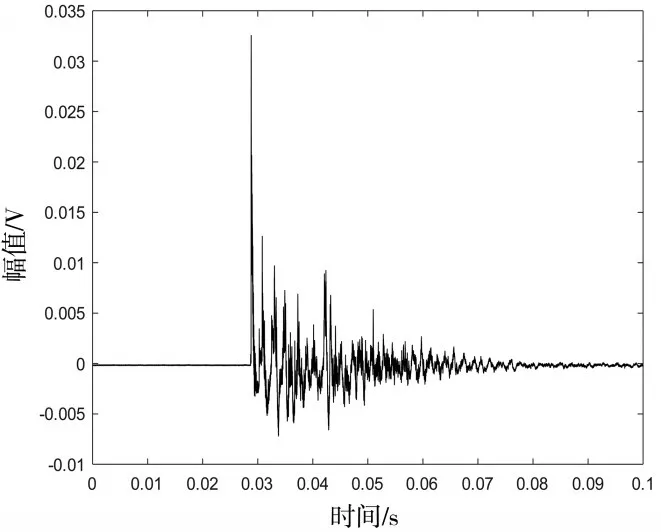
图2 实际冲击波波形图

从图2可以看出该次爆炸试验产生的瞬态信号发生在0.029 s左右，持续时间约为50 ms，超压峰值高达0.033 V、上升时间约为15 μs，高频成分较为丰富，且随着时间推移，其波动范围逐渐减小；非瞬态信号幅度小，近似为无规律的白噪声信号。

1.2 时域门限判别方法

由于冲击波信号的瞬态及非瞬态部分特征区别明显，而本文针对这两部分数据分别需要采用不同的压缩策略，才可进一步提高压缩率，故采用时域门限判别法［9］对瞬态及非瞬态信号进行判别。

该方法需设定一个门限幅度值thT，如果采集到的第i段数据序列Xi(n)中有超过门限值，即满足以下关系：

则取该数据段作为瞬态数据起始段。

2 Exp-Golomb算法原理

本章节首先介绍了Golomb算法、Exp-Golomb算法的基本原理，随后在Exp-Golomb算法的基础上增加了增量预测环节，最后使用增量预测的Exp-Golomb算法对冲击波数据进行压缩处理，分别得出该算法在对于瞬态数据段及非瞬态数据段的压缩情况。

2.1 Golomb算法原理

Golomb算法是一种无损的数据压缩算法，由数学家Solomon W.Golomb在1960年代发明。其只能对非负整数进行编码，当各个数据出现的概率符合几何分布时，编码可以达到最优效果［10］。

Golomb编码是一种分组编码，需要一个正整数参数m作为组内容量参数，然后以m为单位对要编码的数字进行分组。对于任一待编码的非负正整数nu，将其分为两个部分进行表示：所在组编号q以及分组后的偏移部分O。计算公式如下［11］：

对于得到的组号p使用一元编码，偏移部分O则使用固定长度的二进制编码。其中，任意非负整数nu的一元编码即nu位“1”后附一位“0”；或者是nu位“0”后附一位“1”。

Golomb压缩编码的实质是将为0至无限大的数值进行等长分组，如图3所示。

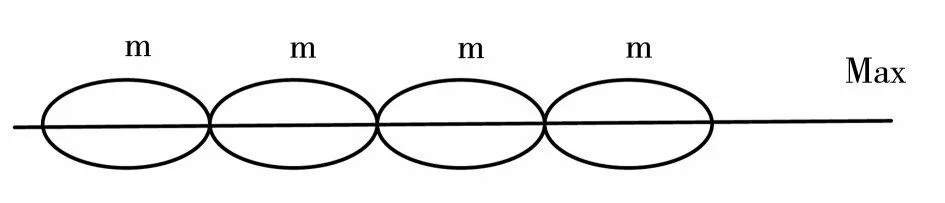
图3 Golomb编码分组示意图

图3为Golomb编码分组示意图，压缩过程就是首先将待压缩数据映射到各个组的各个偏移元素，再传递组号以及组内偏移量，以此达到压缩的目的。最终，对于nu码字长度表示为：

2.2 Exp-Golomb算法原理

Exp-Golomb算法在组容量大小上进行了改进，不再使用固定大小的分组，而使用呈指数增长的组容量［12］。Exp-Golomb需要一个非负整数k作为参数，称之为k阶Exp-Golomb编码算法（EG算法）。其分组示意如图4所示。

图4 Exp-Golomb编码分组示意图

由图4可知，EG算法同样是一种分组编码算法，相较于Golomb算法的定长分组，其按指数增长的变长分组容量能够更好的适应较大数值的压缩。对于任一待编码的非负正整数nu，EG算法同样将其分为两个部分：所在组的编号qe及分组后的偏移量Oe，其计算公式如下：

式中，mq为nu所处的组内长度，其计算公式如下：

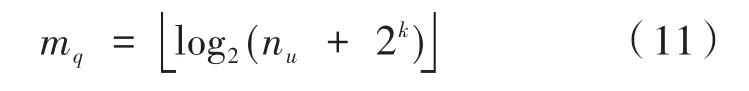
对得到的组号qe使用一元编码，余下部分Oe则使用固定长度的二进制编码，最终对于非负正整数nu的编码码字长度Le为：

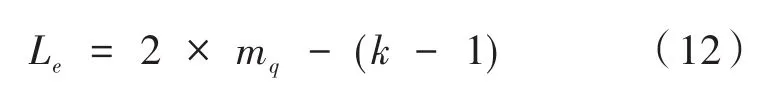
将式（11）带入式（12）得到：

EG算法的组容量呈2的指数倍增长，不同的参数k决定不同的起始分组容量，即k=n时，其起始组的容量为2n。根据数据本身特性适当选取合适k值时，可达到较好的压缩效果。

EG算法对于原始数据序列来说，较小数值的数据会有理想的压缩效果，而对于较大数值的数据来说，压缩率会整体下降。且EG算法通过对不同k值的选取，压缩效果还有很大影响：k取值越小，越适合小值数据的压缩；相反，k值取值越大，越适合大值数据的压缩。

2.3 增量预测Exp-Golomb算法（P-EG）原理

由于EG算法对数值较小的数据压缩效果好，同时为减小数据点间存在的时间相关性［13］，本文在EG算法的基础上增加增量预测环节（PEG算法），通过对原始数据进行增量预测而得到预测残差，对预测残差进行编码即可得到不同压缩阶数k下数据的压缩率。

针对EG算法对数值较小的数据压缩效果好的特性，P-EG算法改变其压缩对象，由对原始数据的压缩改变为对其增量预测后的残差数据的压缩。令原始数据序列为X={x1,x2,x3,…,xn} ，则其增量预测残差X1={x1_1,x1_2,x1_3,…,x1_n}由式（14）求得：

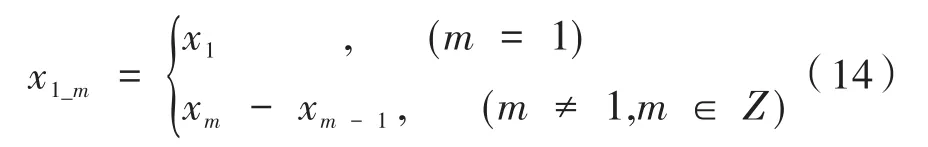
随后对预测残差X1={x1_1,x1_2,x1_3,…,x1_n} 进行零位映射，得到X1′={x1_1′,x1_2′,x1_3′,…,x1_n} ，对应计算公式如下：

对得到的X1′进行EG压缩，即得到在不同压缩阶数k下P-EG算法压缩率。

3 提出针对瞬态数据段的自适应多阶增量预测Exp-Golomb算法

针对瞬态信号的这一特征，本文在P-EG算法的基础上进一步提出基于自适应多阶增量预测的Exp-Golomb算法（MP-EG算法），将数据进行分段多阶增量预测，并且根据其预测值得到其压缩阶数，最后进行EG压缩。

不同于P-EG算法对于整个瞬态数据的增量预测方法，MP-EG算法根据瞬态数据幅值变化程度由大到小的特点，将采集到的瞬态数据均分为三段，并且对三段数据分别进行三阶、二阶、一阶的增量预测。即令N为瞬态数据总量，x为单个数据点所处瞬态数据段中的位置，则各数据点的预测阶数kp满足：

其中，原始数据序列的一阶增量预测残差X1={x1_1,x1_2,x1_3,…,x1_n} 可由式（14）求得，而n（n≥2）阶增量预测残差Xn={xn_1,xn_2,xn_3,…,xn_n}计算公式如下：

在对瞬态数据划分其预测阶数后，可根据式（14）和式（17）求出其多阶预测残差值，再根据式（15）对残差值进行的零位映射。

随后由式（18）得到映射数据xn_m的EG编码的压缩阶数：

根据其自适应后的压缩阶数km再对待压缩数据进行EG压缩，即可得到MP-EG算法压缩率。

4 实验结果

4.1 时域门限判别法对原始数据的划分

采用时域门限判别法对5 psi量程传感器所测得的持续时间为0.1 s冲击波数据进行判别，采样率2 MSa/s，采样精度16位，总数据量为400 Kbytes，得到其瞬态及非瞬态数据的划分如图5所示。

图5 模值累加百分比判别法对原始数据划分

如图5所示，在0.029 s附近开始出现瞬态数据，与此同时，信号幅值超过了0.003 V门限，从而准确区分出瞬态及非瞬态数据。

4.2 P-EG算法对冲击波数据的压缩效果

压缩实验所用数据选取5 psi及50 psi传感器的200 ms的数据，且取50 ms（共计800 Kbytes）作为瞬态数据持续时间，其余条件与4.1节所用数据条件相同。使用EG算法和P-EG算法对5 psi及50 psi冲击波数据进行压缩试验，则不同阶数下EG算法和P-EG算法压缩率对比结果如图6和图7所示。

图6 非瞬态数据压缩率

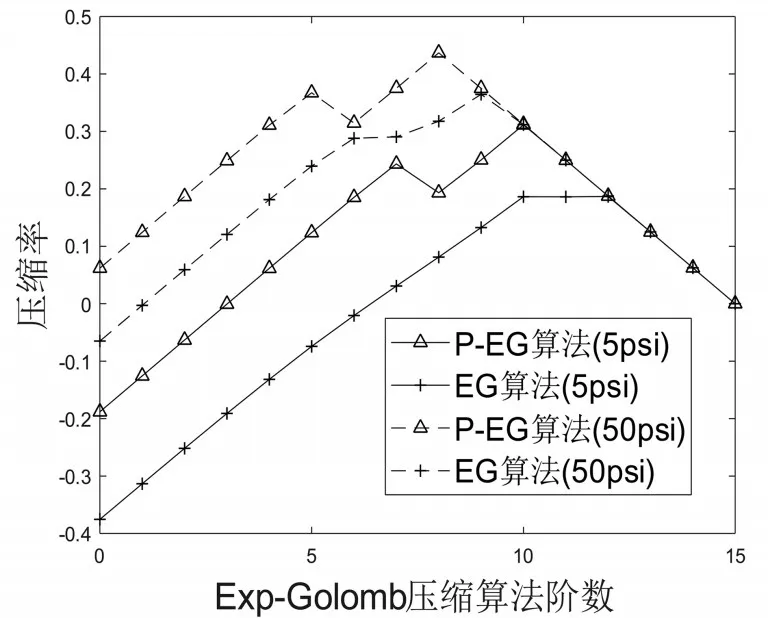
图7 瞬态数据压缩率

从实验结果可以看出，在相同压缩阶数下，P-EG算法的压缩率高于EG算法压缩率。对于非瞬态数据，P-EG算法的最佳压缩率分别达到62.50%（5 psi）、68.75%（50 psi），较 EG 算法提升了12.52%（5 psi）、6.41%（50 psi）。对于瞬态数据，P-EG算法的最佳压缩率分别达到31.14%（5 psi）、43.68%（50 psi），较EG算法提升了12.47%（5 psi）、7.23%（50 psi）。

随着压缩阶数的增加，算法压缩率总体呈先增后减的趋势，是因为过高的压缩阶数会导致数据整体所在的分组容量过大，过低的压缩阶数则会导致数据整体所在的分组数过高，两者均会导致编码位数的浪费。并且随着压缩阶数的增加，两种算法压缩率趋于相同，是由于分组容量的增大使得同一分组内所能囊括的数据个数增加，从而使得编码长度趋于相同。

4.3 MP-EG算法对瞬态数据的压缩效果

采用同样的实验条件，再使用MP-EG算法对5psi及50psi传感器测得的冲击波数据进行压缩仿真试验，则各算法的压缩率对比结果如表1所示。

从表1可以看出，在对冲击波信号进行压缩的过程当中，相比EG算法和P-EG算法，MP-EG算法在同一压缩阶数下的压缩率更高。MP-EG算法对非瞬态数据的压缩率分别达到70.12%（5 psi）、73.15%（50 psi）；对瞬态数据的压缩率分别达到 55.94%（5 psi）、56.17%（50 psi）；总体压缩率达到 66.57%（5 psi）、68.96%（50 psi）。采用MP-EG算法对冲击波数据进行压缩，整体压缩率高于P-EG算法11.91%（5 psi）、6.50%（50 psi），且在瞬态部分的压缩率明显高于P-EG和EG算法，可有效弥补传统压缩算法信息易丢失且对瞬态数据压缩率低的缺点。