荧光渗透探伤裂纹长度测量技术研究

王赫，白素平，闫钰锋

（长春理工大学 光电工程学院，长春 130022）

零件由于各类应力的作用会出现不同程度的损伤。在工业生产中，对于大部分结构较为简单的零件，表面产生的裂纹会随着运作过程中应力的不断作用而逐渐延展，这使得设备整体的工作安全和工作效率受到了影响，并随着裂纹的逐渐扩大引起设备的机械性能大幅度下降。因此，对零件进行表面裂纹检测并及时更换或处理问题零件在工业生产中具有重要的意义。

近几年一些裂纹检测系统相继问世，诸如Crack Viewer、IRP-100等裂纹检测系统，它们虽然可以实现裂纹信息的提取，但采集结果中的干扰信息较多。为了进行裂纹的检测，Hutchinson等人［1］使用canny滤波器和小波变换相结合的方法；Iyer等人［2］使用了数学形态学的方法；Miwa等人［3］则利用了分水岭分割算法。然而上述这些方法过度专注于将线性形状特征做为裂纹的主要特征，因此只能将检测出的一些线状轮廓做为实际裂纹的近似，一方面它们无法十分准确地检测出完整的裂纹，另一方面测量对象也受到自身表面形状的限制，进而就无法得到相对准确的裂纹长度信息［4-13］。

为了得到裂纹完整且准确的图像信息，在进行裂纹图像处理前，通过采用荧光渗透探伤对待测零件进行渗透处理。在暗室环境中，荧光材料渗透到缺陷裂纹中，使得裂纹部分的对比度大大增强，最终采集到的图像上，裂纹的轮廓清晰且连贯，同时可形变标尺可以随着零件的表面形状展开，此时标尺与裂纹的形变状态相同，在相机下不管缺陷零件表面为何种形状，在图像中单个像元所对应的实际长度是固定的，通过对应像元的实际长度相叠加，不但可以实现对工件复杂表面裂纹长度的计算，同时由于像元的尺寸微小，让测量精度大大提高。

1 荧光渗透探伤

荧光渗透探伤是一种以毛细管现象为基础，用于检查表面开口缺陷的无损检测手段。是五种常规无损检测方法中的一种（射线探伤、超声波检测、磁粉探伤、涡流检测）。同其他无损检测方法一样，荧光渗透探伤也是在不损坏被测对象使用性能的前提下工作的。

本文中应用水洗型荧光渗透探伤法来捕获零件表面的缺陷区域图像。根据所使用显象剂的种类水洗型荧光渗透探伤的工作流程图，如图1所示。

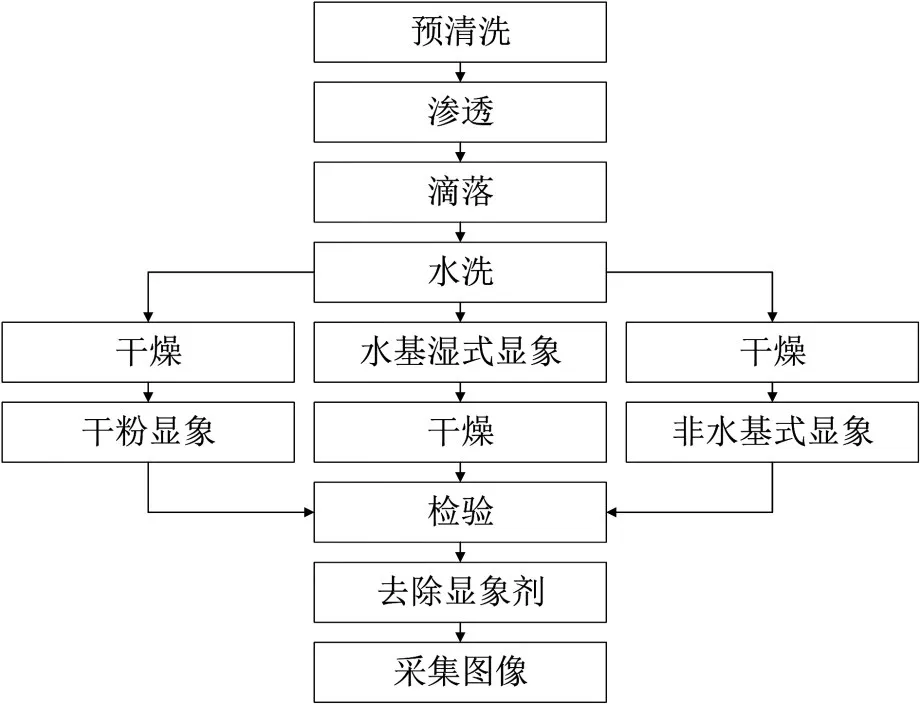
图1 水洗型荧光渗透探伤的工作流程图

2 裂纹缺陷长度检测

近几年，国内外有不少学者都在尝试用数字图像处理的方法，来检测各种物体表面裂纹缺陷的尺寸。其目的都是在存在噪声的物体表面图像中检测出裂纹轮廓并将其标注出来。这样做的主要问题在于检测出的裂纹轮廓可能会出现断裂，导致检测不完整，并且由于相机与CCD精度问题使得裂纹识别的准确率相对较低［14-16］。为解决这些问题，采用经过荧光渗透处理后的零件图像，加强裂纹处的图像对比度，根据实际情况无需进行图像增强处理。同时，凭借在缺陷区域贴加荧光标尺，以比例换算的方式降低相机与CCD带来的精度误差。

2.1 图像的去噪处理

在对裂纹缺陷图像区域进行处理时，只针对裂纹所在的小区域图像做相应处理可以有效减少计算时间、提高算法运行效率。本文中所采用的裂纹缺陷计算方法，所感兴趣的特征区域为裂纹及标尺所在窗口。裂纹与荧光标尺边缘都需要在图像上清晰体现。主要通过迭代阈值法来实现特征区域的提取。

迭代阈值法中阈值化处理主要是为了确定裂纹与标尺的初始窗口。图像的分割精度极大程度上依赖于所确定的阈值是否准确。迭代阈值法是阈值法图像分割中比较有效的方法，通过迭代的方式来求出分割的最佳阈值，具有一定的自适应性。迭代阈值法的步骤如下：

（1）确定参数T0，并选择一个初始估计阈值T1；

（2）用阈值T1分割图像。将图像分为两部分：灰度值大于T1的像素集合G1与灰度值小于T1的像素集合G2；

（3）分别计算G1及G2中所有像素的灰度平均值，记为μ1与μ2，则有新的阈值：

（4）若 |T2-T1|＜T0，则认为T2为最佳阈值；反之，将T2赋值给T1，重复步骤（2）-步骤（4），直至得到最佳阈值位置。

2.2 裂纹尺寸的计算方法

假设标尺的尺寸为Amm×Bmm，且可求得标尺长所占像素个数为n1，宽所占像素个数为n2。将裂纹的图像细化分块，即将裂纹长度以单个像元长度为单位分割成许多小单元，得到裂纹长所占像素个数为。

分析标尺，对于标尺的长，单个像元所代表的实际长度通过比例换算可以得到，即：

同理，对于标尺的宽，单个像元所代表的实际长度通过比例换算得：

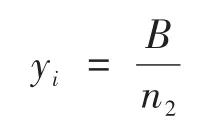
建立坐标系XOY，将裂纹沿X轴分成n段微弧dx1,dx2,…,dxn，由于单个像元尺寸足够小，近似将这些微弧看成直线，如图2所示。

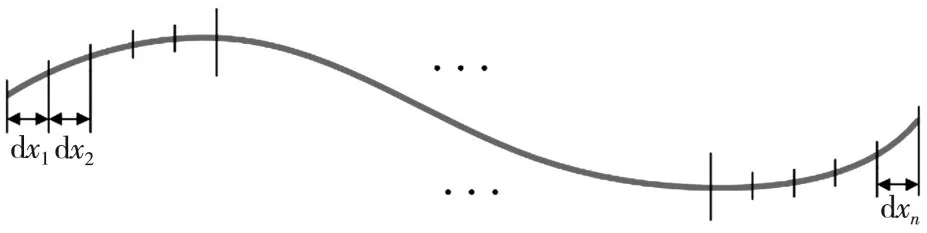
图2 裂纹分割图

在实际图像中dx实际上覆盖了一定数量组成的列像元，分别对dx1,dx2,…,dxn取中心点，共计得到n个特征点，每相邻两点之间用直线连接，共计有n-1条线段z1,z2,…,zn-1。则以X轴为基准，判别zi（i=1，2,…,n-1）与X轴的夹角θi。针对第i（i=1，2,…,n-1）个中心点，当θi＜ 45∘时，在其所在的像元列，dxi的长度为xi；当θi≥ 45∘时，在其所在的像元列，dxi的长度为yi。针对最后一段微弧dxn，其长度的选择由第n-1个夹角θn-1的大小来决定，判别方式同上。最终裂纹的长度为：

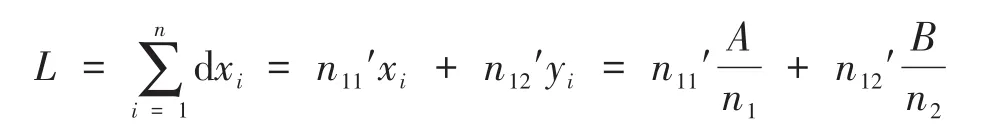
3 精度分析与实验结果

3.1 实验精度分析

在图像采集时，裂纹与标尺经由统一光学系统缩放，最终成像在同一个CCD上，可使被测裂纹与标尺所成的像拥有相同的畸变。被测裂纹与标尺在拍照成像的过程中具有相同的系统误差，且两者的系统误差可以起到相互补偿的作用，因此，在对裂纹的测量过程中，误差主要由CCD成像时单个像元引起，同时标尺的尺寸误差也会影响测量精度。

3.1.1 CCD单个像元引起的误差

由于在图像采集时，裂纹与标尺被放入同一视场内进行比例换算，但因为CCD分辨率不足以精准地用整数个像元表征裂纹与标尺的尺寸，所以CCD单个像元引起的误差最大时分如下2种情况。

3.1.2 标尺的误差

标尺根据其生产、工作环境等因素，其误差通常分为尺长误差ν1与标尺使用时的测量环境温度误差ν2，从标尺生产的角度，通常采用电子测量显微镜来测量，因此尺长的测量精度可达±1 μm，即δ1≤±1 μm；同时在正常室内温度下工作，标尺的形变最大约为±3 μm，且呈偶然性，即δ2≤±3 μm。

3.1.3 误差的合成

通过上述分析可知，CCD单个像元所引起的误差与标尺的误差均为随机误差，在测量实践中，各个单项误差的随机误差和测量结果的总误差也常以极限误差的形式表示，由于极限误差可通过标准差来表示，故合成后的总误差可写为：

由于所选用的远心镜头光学倍率为1，所以CCD单个像元所引起的误差可以直接带入计算。将CCD单个像元所引起的误差与标尺的全部误差代入总误差公式，计算长度的合成误差。合成后长度的误差为：

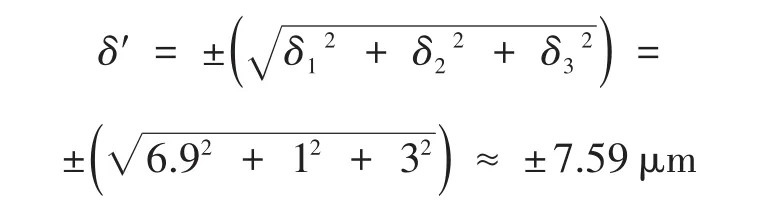
由于裂纹分布不是水平或垂直的，根据长度方向的作用误差，得出测量长度的结果表达式为：

裂纹与标尺所占的像元个数比可近似等于长度比，已知裂纹长度最长为5 mm，标尺的边长为3 mm，所以有：

故裂纹长度的极限误差为：

3.2 实验原始图像

经由荧光渗透探伤过程处理过后的表面带有缺陷的零件，其表面粘贴着涂有荧光颜料的标尺，标尺的尺寸为3×3 mm2，由于对比度的差异，裂纹缺陷在图像中较为清晰，为了方便完成裂纹长度的测量，实验时通过激光打标机在薄片金属零件上，刻划了3道长度不同的划痕作为待测裂纹。为方便手工测量，激光打标机在薄片型零件上刻划的模拟裂纹均为直线，经由手工测量三道划痕的长度分别为4.98 mm、3.86 mm、2.35 mm。且由于激光打标机工作时光束能量较高，薄片金属零件受热发生形变，其表面由平面变为带有一定弧度的不规则表面。图像采集实验的实验装置图如图3所示。

图3 图像采集实验装置图

该装置所采集到的模拟裂纹区域图像如图4所示。

图4 采集到的裂纹区域图像

4 实验结果分析

运用裂纹长度检测算法测量裂纹图像中的裂纹长度，通过去噪及阈值化处理后所得的图像结果如图5所示。

图5 迭代阈值分割后的裂纹图像

测量所得裂纹长度结果分别为4.987 4 mm、3.872 3 mm、2.340 2 mm，与激光刻制的标准值相比测量误差分别为 7.4 μm、12.3 μm、-9.8 μm，均位于精度分析中±18.9 μm的测量精度范围内。

5 结论

本文根据常见裂纹长度检测系统的特点和裂纹长度检测相应的技术指标要求，从渗透探伤和图像处理相结合的角度出发，提出一种在采用渗透探伤的情况下，通过累加单个像元尺寸，实现对工件复杂不规则表面裂纹长度计算的方法。相比于过去常用的裂纹尺寸检测方法该方法具有更高的测量精度，且不受面型种类的影响。通过相应的精度分析计算后得到该算法的裂纹长度测量精度为±18.9 μm，实际实验测量情况也表明，精度分析计算所得测量精度范围合理。