基于蒙特卡洛法的激光通信地面站轴系误差分析

王天宇 ，张家齐 ，张立中 ，王桂冰

（1.长春理工大学 机电工程学院，长春 130022；2.长春理工大学 空间光电技术国家地方联合工程研究中心，长春 130022；3.长春理工大学 空地激光通信技术重点学科实验室，长春 130022）

激光通信地面站是星-地激光通信链路的重要组成部分，其主要功能是与高轨和低轨卫星载荷进行跟踪、捕获和通信［1］。随着激光通信技术的不断发展，通信距离和速率不断提升，地面站望远镜口径不断增加，使跟踪架结构也随之增大，大型零件配合时的误差将对轴系精度产生较大的影响，提高加工精度和轴承精度，会增加零件加工难度，提高了成本，轴系精度过低，则会导致整机系统的工作不稳定，严重时会导致项目的失败［2-3］。更加科学合理的分析和分配地面站跟踪架轴系精度，一方面可以降低加工、装校难度，在大规模生产中可以降低成本；另一方面可以准确预估轴系精度对系统性能的影响，使仿真更为准确［4］。

目前对轴系误差分析主要使用极值法，例如中科院的4 m级地基光电望远镜跟踪架，计算轴系中的最大误差值，对轴系中可能产生的最大值进行预估［5］。但实际加工装调过程中误差的最大值出现的概率很低，特别在大规模生产时，会使成本和装调难度大幅度提升；同时极值法很难建立各种误差在综合作用下跟踪架的运动模型，零件在加工时，在公差范围内存在不确定性。针对这几个问题，本文以激光通信地面站为研究对象，使用蒙特卡洛法结合Adams对轴系误差进行分析，可对轴系误差更准确预估，其图像及响应报告可以有效准确的反应不同公差的波动情况，并分析出轴系误差设计敏感因子，可在设计时较严格控制敏感误差公差范围，对不敏感因素适当放松其公差标准，降低加工和装配要求；通过运用蒙特卡洛法，模拟轴系部件在实际加工时的随机性，准确的展示出位移跳动情况，避免了最值分析的单一性，在轴系误差分配上目的性更强、更准确，为轴系公差设计分配提供重要的指导作用［6］。

1 建立跟踪架基本运动模型

1.1 建立跟踪架模型

通过SolidWorks三维绘图软件建立与实际工况一致的激光通信地面站跟踪架数模，如图1所示。该地平式跟踪架分为：方位轴系、俯仰轴系、U型架和四通。通过两个轴系的回转运动，可使整个跟踪架实现方位轴在0°～360°范围内运动，俯仰轴在 0°～85°范围内运动，轴系晃动为 3″以内。

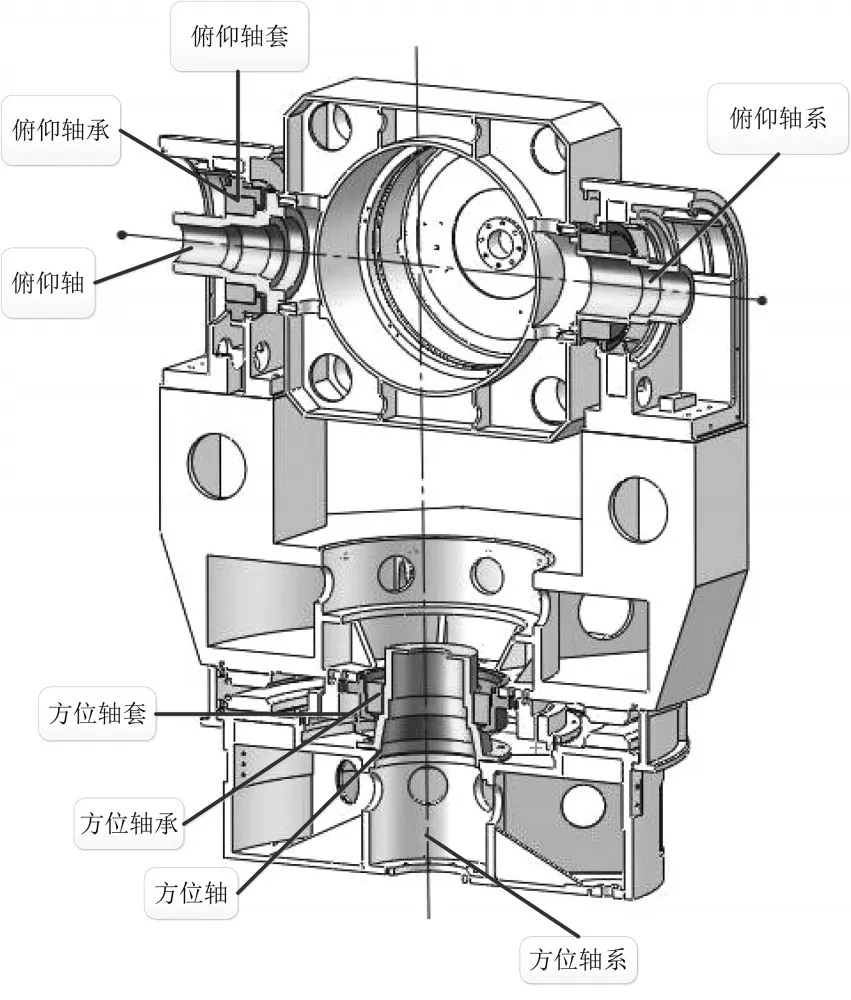
图1 大口径地面站跟踪架三维模型

1.2 建立跟踪架运动模型

使用软件对跟踪架装配体关系进行仿真，如图2所示，建立方位轴套和U型架约束，实际工作中，方位轴套和U型架使用螺钉相连接，为模拟实际工况，以固定副模拟螺钉固定连接，选择方位轴套和U型架，以轴套中心点作为二者的固定副连接点，建立方位轴套和U型架的固定约束，后分别建立大地和方位轴、方位轴和轴承、轴承和轴套等其他零部件的约束，如表1所示。

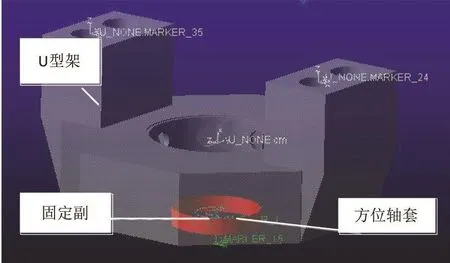
图2 方位轴套和U型架固定约束

表1 轴系各零部件约束副

由于实际加工中零件误差大小具有的不确定性，需要在Adams View中对运动轴系之间存在误差进行参数化设置，对于关键的运动部件的三维模型在Adams View建立并使其参数符合实际加工情况。理想型运动时方位轴中心与轴承中心应重合，由于轴承和轴在加工过程中会产生不确定误差，导致轴中心与轴承中心在运动时不重合，使整机产生位移误差，为了简化运动，故将方位俯仰轴与轴承内圈的配合运动，简化为方位俯仰轴参考点绕其轴线运动，模型中建立参考点，如表2所示。

表2 轴系参考点描述

1.3 建立跟踪架驱动

激光通信地面站采用地平式跟踪架结构，两个轴都采用传统的直流力矩电机驱动，在施加驱动时满足两轴绕轴线匀速旋转，便于观察加工随机性而误差不确定性，为模拟跟踪架全部运动轨迹的匀速工作状态，一定时间内完成方位轴转动360°，俯仰轴转动85°，满足模型与实际运动一致，使得最终仿真结果与实际相符，其方位俯仰控制驱动如下，通过step函数控制在规定时间内匀速运动：

（1）方位轴系添加驱动

sin（time，0.0，18d，20，18d）为方位轴系添加sin驱动，一定时间按18s匀速旋转360°。

（2）俯仰轴系添加驱动

sin（time，0.0，4.25d，20，4.25d）为俯仰轴系添加sin驱动，一定时间按4.25s匀速旋转85°。

2 蒙特卡洛法分析轴系运动

2.1 地面站轴系误差分析

轴系回转误差，包括线位移和角位移误差。影响因素颇多，本文主要讨论轴系误差对大口径望远镜的回转运动精度的影响。

俯仰轴系精度，主要由U型架两端轴系安装孔和角接触球轴承、深沟球轴承间隙配合时产生的径向间隙、圆柱度和轴承本身径向间隙等。

方位轴系精度，主要由方位轴与与其配合的圆柱滚子轴承产生的径向间隙、圆柱度和轴承本身径向间隙等［7-9］。

2.2 传统极值法选型

在选择轴承及零部件配合时，传统极值法采用激光通信地面站的指标作为设计选型依据，俯仰方位均采用精度为P4的轴承［10-11］。以俯仰轴为例，按照静圈间隙，动圈过盈的设计原则，其轴承内圈与轴为过盈配合，轴承外圈与轴套间隙配合，轴承外径为，轴套采用 H5 配合，其内径为，由配合间隙Δd所引起的整周径向晃动误差Δc为：

其配合后俯仰轴系间隙最大为δ1=0.0175mm，轴承环圆度误差为δ3=0.010 mm，同理其配合后方位轴系间隙为δ2=0.018mm，方位轴端面跳动δ4=0.010 mm；方位轴系到中心点距离L1=500 mm，俯仰两轴跨距L2=500 mm，轴系精度计算方法如下：

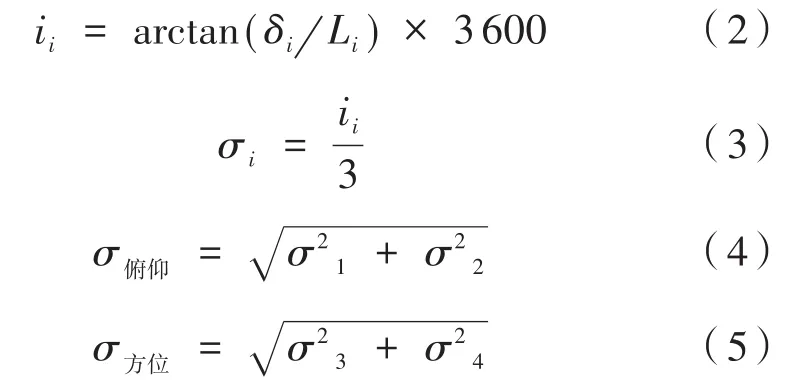
得到俯仰轴系晃动为2.94″，方位轴系晃动为2.99″，均在3″以内，符合伺服调试标准。

2.3 蒙特卡洛法

蒙特卡洛分析法（Monte Carlo method）又称统计模拟法，是一种采用随机抽样（Random Sam⁃pling）统计来估算结果的计算方法，由于计算结果的精确度很大程度上取决于抽取样本的数量，一般需要大量的样本数据［12］。动力学蒙特卡洛法的基本原理为：

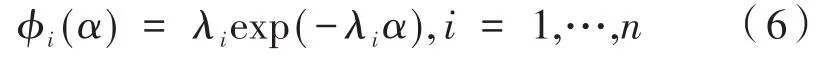
n个独立事件，相继发生需要的时间φ的泊松过程，λi为第i个事件发生的速率，其中存活函数为：

第i个事件发生的概率密度为：

故发生概率为：

由于在工程加工时产生的误差在公差允许范围内为随机性的，所以采用蒙特卡洛方法模拟分析跟踪架运动最接近实际运动，可以得出可靠的运动曲线。

2.4 用蒙特卡洛选型

根据大口径地面站指标要求，对轴承和配合进行初始选择，首先按照GB/T307-94国家标准粗选轴承精度，暂选轴承精度为P0，其余根据中华人民共和国国家标准GBT275-93滚动轴承与轴配合选择轴孔偏差，根据实践经验综合考虑其公差范围，选择轴系间的公差选择如表3所示。

表3 轴孔各零部件公差表（单位/mm）

2.5 基于蒙特卡洛法提取随机数

在运用Adams insight软件在公差范围内提取随机数分为normal（正态分布），weibull（布尔分布），uniform（均匀分布），discrete（泊松分布）等［13-14］。由于机械加工时产生的误差是随机的，提取的随机数服从正态分布，以方位轴系中心偏移为例，根据表3尺寸链相加计算出中心整体偏移公差为0.5 mm，将偏移公差反映在在笛卡尔坐标系中，得出方位在全局坐标系中X、Y方向有偏差，俯仰在全局坐标系中Y、Z方向有偏差，本文设定此偏差在两方向为线性不相关并且相等，根据公式（9）：

式中，x为X方向上偏差；y为Y方向上的偏差。得出Δd1= Δd2= ±0.35mm。

3 跟踪架的运动仿真及分析

根据跟踪架的实际运动情况，基于全局坐标系，设置实际仿真时间为20 s，仿真步数为2 000步，进行100次蒙特卡洛模拟仿真。

得出图像如图3-图5所示，图中曲线分别为在俯仰方位有间隙时目标位移变化曲线、对间隙进行优化后目标位移变化曲线、单独俯仰有间隙时目标位移变化曲线和单独方位有间隙时目标位移变化曲线。

图3 100次间隙实验X位移变化

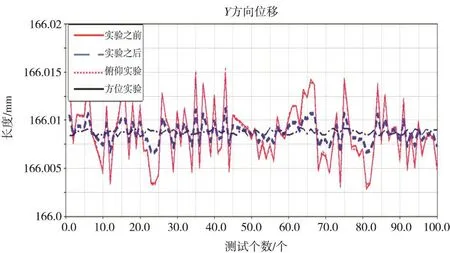
图4 100次间隙实验Y位移变

图5 100次间隙实验Z位移变化

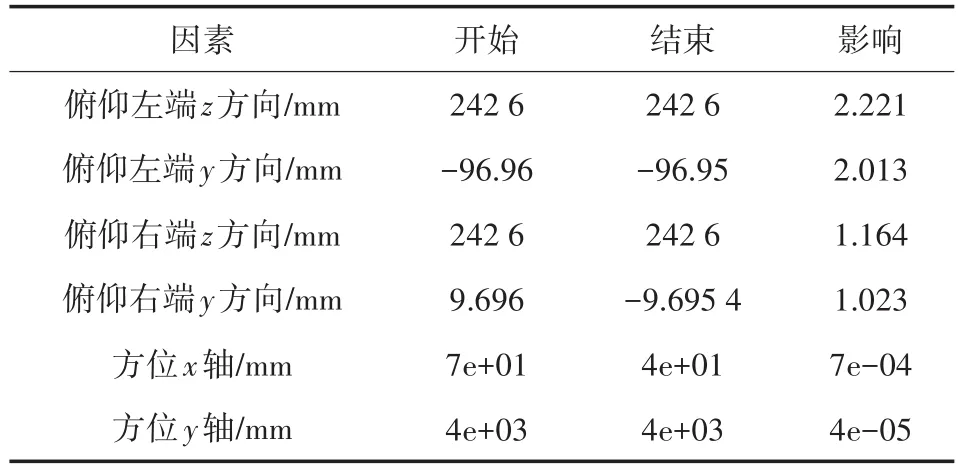
表4 轴系参考点影响因素

在有间隙时，方位轴系和俯仰轴系中的零件发生碰撞，使其位置不能平稳的过渡，位移跳动大，曲线抖动强烈，幅值大，从图3中的曲线可以看出来俯仰轴系和方位轴系间隙对位移X方向影响相当；从图4、图5中可看出俯仰轴系间隙为Y、Z方向上的位移影响的主要因素，而方位轴系间隙几乎对Z轴方向上位移没有影响，通过Ad⁃ams生成的响应报告，可以得出影响位移跳动的最大因素，如表4所示，从图表可以得出俯仰轴间隙对位移影响最大，在设计时需尽量减小俯仰轴系中的配合间隙，以确保精度。

根据图3-图5所示，整机轴系在不同间隙时位移跳动变化很大；经过计算俯仰轴回转误差超出指标，不符合伺服控制调试要求，为伺服调试增加难度。通过Adams生成的响应报告对轴系间隙进行调整，俯仰轴系选用精度为P5的轴承，减小俯仰配合间隙至轴套内圈290+0.03+0.01、350+0.03+0.01，从图3-图5中可以清晰的对比出调整之后的整机运动更稳定，相比调整之前的跳动曲线，幅值更小，跳动小，保证跟踪架重复定位精度高、平稳性好，满足伺服调试要求。根据位移变化范围得到调整前后的公差范围，按照公式（1）-公式（2）计算得到方位俯仰轴系晃动位移σ：

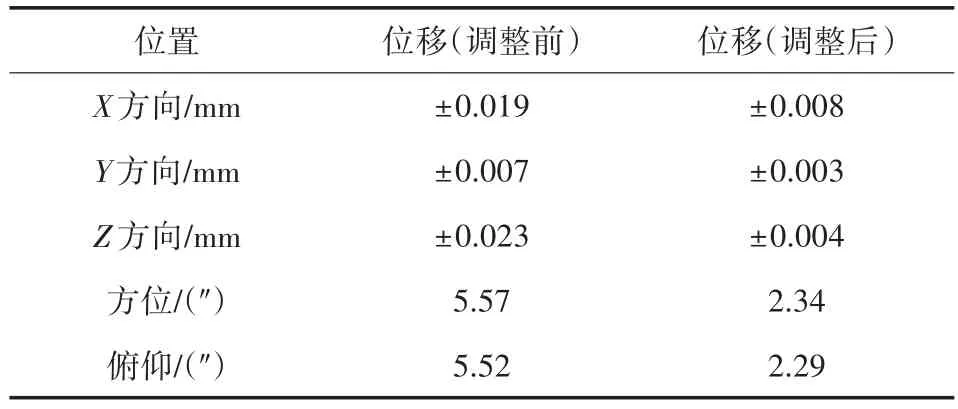
表5 调整前后位移变化对比

经蒙特卡洛法可以更精确的分配轴系间的误差，适当放宽轴承精度，相比传统方法选用精度为P4轴承，轴套高精度公差，经曲线与报告总结，激光通信大口径地面站俯仰轴系轴承采用P5精度，即可满足轴系晃动对伺服调试的要求，相比选用更高精度的P4轴承和轴套高精度公差，降低了制作成本，同时也降低了安装调试要求，在大量产品生产时，提高了整体的生产经济性。

4 跟踪架的伺服控制试验

根据上文所述相关设计完成大口径地面站整体结构设计、加工与装配，搭建如图6所示，轴系晃动测量图，测试轴系晃动误差，得到方位轴系俯仰轴系晃动满足伺服调试要求，故搭建图7所示的大口径地面站测试系统。其中电机选取成都电机厂生产的直流力矩电机；角位置反馈元件选择雷尼绍公司的RESOLUTETM系列绝对式光栅系统，具有32位分辨率。

图6 轴系晃动测试示意图

图7 测试现场

为测试所设计大口径地面站的动态跟踪性能，对系统进行等效正弦跟踪测试。正弦引导的最大速度为1s，最大角速度为1s2，等效正弦曲线为y=sint。正弦跟踪曲线如图8所示，正弦跟踪误差曲线如图9所示，其中最大跟踪误差为 9.6″，RMS 值为3.15″。

图8 正弦跟踪曲线

图9 跟踪误差曲线

5 结论

本文针对激光通信大口径地面站地平式跟踪架轴系配合间隙引起的精度问题进行研究，利用蒙特卡洛方法结合Adams insight的进行轴系间隙的随机抽样，并进行运动模拟仿真，在后期的曲线处理对比发现俯仰轴系间隙对整体位移跳动影响明显，方位轴系晃动到达5.57″，俯仰轴系晃动达到5.52″，经曲线和响应报告进行调整，方位轴系晃动 2.34″，俯仰轴系晃动 2.29″，满足伺服调试条件，此方法可以合理的分配轴系误差，放松不敏感因素，方便装调，在大规模生产加工时会大幅度降低制造加工成本，对零件的加工和轴承的选型起到指导作用。