基于Copula方法处理随机前沿模型的正偏度问题

冯冬发,张 涛,李 奥

(1.中国社会科学院大学(研究生院) 数量经济与技术经济系,北京 102488;2.中国社会科学院 数量经济与技术经济研究所,北京 100732)

一、引 言

随机前沿模型假设其复合扰动项ε由相互独立的两部分v和u相减构成,其中v服从正态分布,刻画了厂商无法控制的环境因素与被解释变量的测量误差,u服从半正态分布,刻画了厂商的技术无效率,即实际产量与理想产量之间的差距[1]。在上述设定下,ε的偏度应始终小于零,但在实际测算过程中,回归方程残差项的偏度却可能取值为正,由此产生正偏度问题,进而导致模型错判样本内厂商不存在技术无效率[2]。

早期研究认为正偏度问题是小样本问题[3],可以通过扩充样本量、适当变换生产函数形式、调整回归元等方式来加以规避[4]。后续学者发现正偏度问题在大样本中同样时有出现,该问题产生的根源在于模型对技术无效率的分布假设过紧,其偏度始终大于0,极大地限制了复合扰动项偏度的取值范围[5]。如果假设技术无效率服从均匀分布或二项分布,则能够在经典模型失效的情形下,依然取得厂商技术效率的合理估计值[6-7]。事实上,复合扰动项偏度受到v的偏度、u的偏度、v与u的相关性等三部分内容的影响[8],由于修改随机扰动项v和u的分布设定往往缺乏经济学理论的支持[9],所以研究者的目光逐渐转向允许两部分随机扰动项之间存在相关性[10]。Copula方法可以描述变量之间的相关性,多用于金融领域研究[11],在解决随机前沿模型的内生性问题上也有较多的应用[12-14],但将其用于研究正偏度问题的文献尚不多见,这部分文献为获得参数估计量的解析解,往往对v和u的分布施加一些不常见的分布设定,限制了这些研究成果的应用前景。

数值模拟方法的广泛应用为处理随机前沿模型的正偏度问题提供了新的思路[15]。本文将在保留经典模型关于随机扰动项v和u各自分布设定的前提下,使用Copula方法刻画两者之间的相关性,基于极大模拟似然估计法给出模型参数与厂商技术效率的估计值。该模型设定具有两处优点:一是假设两部分随机扰动项之间存在相关性,即允许来自厂商控制之外的环境冲击对厂商的技术效率产生影响,显然具备合理的经济学含义。二是保留了经典模型中关于随机扰动项分布的设定,是对经典模型的自然拓展,当两部分扰动项v和u相互独立时,本文使用的模型设定便与经典模型完全一致,可以使用标准统计检验程序来判断两部分随机扰动项之间相关程度的显著性,以此作为模型选择的依据。

二、研究设计

(一)模型设定

借鉴Aigner等的模型设定[1],给出如下形式的随机前沿模型:

yi=f(xi;β)+εi

εi=vi-ui

(1)

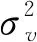
(二)相关性度量

Sklar定理指出:任意一个多元联合分布函数均可分解为其边缘分布和一个刻画相依结构的Copula函数,如果边缘分布连续,则Copula函数能够被唯一确定[16]。假设vi的密度函数为g(vi),分布函数为G(vi),ui的密度函数为h(ui),分布函数为H(ui)。由Sklar定理可将vi和ui的联合分布函数M(vi,ui)表示为:

M(vi,ui)=Cθ[G(vi),H(ui)]

(2)

式(2)的Cθ(·,·)是刻画了vi和ui相依结构的Copula函数,θ为该Copula函数的参数向量,假设该参数向量与模型的参数向量β之间不存在相同元素。如果Copula函数取乘积Copula,即Cθ(x,y)=xy,则有联合分布函数M(vi,ui)=G(vi)H(ui),意味着vi和ui相互独立,此时式(1)所描述模型与经典随机前沿模型完全一致。当Copula函数取其它形式更为复杂的设定方式时,模型便允许两部分随机扰动项之间存在相关性,更加贴近现实。

由vi和ui的联合分布函数可以给出两者的联合概率密度函数m(vi,ui),如式(3)所示:

(3)

式(3)的cθ(·,·)被称为Copula密度函数,式(3)实际上将随机变量的联合概率密度函数分解成了边缘密度函数和一个刻画相依结构的Copula密度函数。

Copula函数刻画了随机扰动项vi和ui之间的相关性,其强弱与参数向量θ有关。但Smith指出θ并非良好的相关性度量指标,建议使用Spearman相关系数Sρ来度量随机变量间的相关性[10],其具体形式如式(4)所示:

(4)

Spearman相关系数有两处优点:一是非常直观。取值范围为[-1,1],随机变量正相关时取值为正,负相关时取值为负,不相关时取值为0,绝对值越大代表相关性越强。二是Sρ的数值大小仅与所选择的Copula函数及其参数向量θ相关,与随机变量服从的边缘分布无关,具有不变性(invariance)。

不同的Copula函数选择会对估计结果产生影响,本文将根据赤池信息准则(AIC)在若干常用的Copula函数中选择最合适的一个。估计出模型参数后,可以对Sρ做原假设为H0:Sρ=0的假设检验,如果拒绝原假设,认为随机前沿模型中两部分扰动项之间存在显著的相关性,应考虑使用本文的模型设定。如果无法拒绝原假设,则使用经典的随机前沿模型仍是合理的。

(三)参数估计

将式(1)代入到式(3)中得到vi和ui的联合概率密度函数m(vi,ui),调整变量后计算出εi和ui的联合概率密度函数m(εi,ui),如式(5)所示:

m(εi,ui)=g(εi+ui)h(ui)cθ(G(εi+ui),H(ui))

(5)

对式(5)做关于ui的积分,可以求出εi的边缘分布,如式(6)所示:

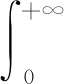
=Eu[g(εi+u)cθ(G(εi+u),H(u))]

(6)

式(6)中的Eu是关于随机变量u的数学期望算子,求得复合扰动项εi的概率密度函数后,可以给出模型的对数似然函数,如式(7)所示:

(7)

基于式(7)使用极大似然法估计模型参数的难点在于:式(6)只有在少数特殊情形下才有解析解。本文将借鉴Greene提出的极大模拟似然估计法来完成模型的参数估计,这种方法的核心思路是使用大样本抽样的样本均值来近似总体分布的期望值[15]。式(6)已将mθ(εi)改写成数学期望的形式,只要在技术无效率项u服从的总体分布中抽样R次,计算函数g(εi+u)cθ(G(εi+u),H(u))的样本均值,由大数定理可知:

(8)

据此可以给出mθ(εi)的模拟数值解,在此基础上使用极大似然估计法便可以给出模型的参数估计值,这种基于大样本模拟抽样的估计方法就被称为极大模拟似然估计法。

(四)技术效率的最优预测值

随机前沿模型的核心在于估计厂商的技术效率值,正偏度问题带来的最大影响正是无法给出合理的技术效率估计值。借鉴Battese和Coelli提出的厂商技术效率最优预测值[17],给出如式(9)所示的厂商技术效率值估算方法:

(9)

式(9)的分母与式(6)完全相同,分子可以参照式(8)给出的模拟抽样方法进行估计,两相结合可以计算出厂商技术效率的最优预测值。

三、蒙特卡洛实验

(一)实验设计

引入如式(10)所示的单投入单产出随机前沿模型:

yi=β0+xiβ1+vi-ui

(10)

蒙特卡洛实验首先考察两部分随机扰动项之间相关性强弱对于模型最小二乘残差项的偏度及厂商的平均技术效率估计值的影响,以此说明正偏度问题的存在及其引发的后果。取样本容量为N={50,500},将θ的取值范围[-1,1]均等分为1 000个子区间,取每个区间的中点作为θ的实际取值,使用R语言的frontier包完成模型参数的估计并计算厂商的平均技术效率。对于每一个θ的取值,模拟实验均重复100次,取其平均值用于最终的结果展示。

此外,蒙特卡洛实验还需要验证本文所提出估计方法的有效性与稳健性。为考察不同程度相关性的影响,令θ={0,0.5,0.9},相应的Spearman相关系数为{0,0.48,0.89},分别代表两部分随机变量之间不存在相关性、存在中等程度相关性和存在高度相关性三种情形。此外,本文还设计了三种不同的样本容量N={20,300,1 000},分别代表了小样本、中等样本和大样本三种情形,模拟实验均重复1 000次,取其平均值用于最终的结果展示。

本文在模拟实验中具体考察了三种不同估计方法,分别是:经典随机前沿模型估计法(以下简称SF),这种估计方法假设vi和ui相互独立,是目前学术界使用的最为广泛的估计方法;基于Normal Copula的极大模拟似然估计法(以下简称NC);基于FGM Copula的极大模拟似然估计法(以下简称FC)。NC选择的Copula函数是用于生成模拟数据的Copula函数,FC选择的Copula函数则与设定的总体分布不符,后者往往是现实中最常见的情形,即允许随机扰动项之间存在相关性,但选择了不准确的刻画方式。通过考察FC估计量的统计性质,可以在一定程度上评估本文所提出估计方法的稳健性。两个Copula函数之间不存在相互嵌套的关系,分别以不同的方式刻画了两部分随机扰动项之间的相关性,但都将乘积Copula视为其特殊情形,即将经典随机前沿模型作为它们的特例,据此可以通过标准统计检验程序判断两部分随机扰动项之间是否存在相关性,进而评估使用经典随机前沿模型的合理性。

模拟实验具体考察的内容是模型参数和厂商技术效率的估计精度。借鉴蒋青嬗等人的做法,本文将从偏差、标准差和均方误差三个方面来评价模型参数的估计精度,使用均方误差来判断厂商技术效率的估计精度[12]。所谓的偏差是参数估计量与其真实值之差,其本身有正有负,为防止参数估计量的正向偏差与负向偏差之间存在中和抵消,本文使用的是偏差的绝对值。标准差计算的是每次模拟实验得到的1 000个估计量的标准差,而非参数标准差估计量的均值。均方误差指的是参数估计量与其真值之间差距的平方的均值,对于技术效率而言,其真值为exp(-ui)。显然,本文计算得出的偏差、标准差和均方误差均为大于零的正数,数值越小代表估计精度越高,反之则代表估计精度越低。

(二)结果展示

图1和图2分别给出了样本容量为50和500时,第一部分模拟实验的结果。图形的横轴代表Normal Copula的Spearman相关系数Sρ,其取值范围为[-1,1],刻画了随机前沿模型中两部分随机扰动项之间的相关性,取值为0代表两者不相关,正值代表正相关,负值代表负相关,数值越大代表相关性越强,反之则越弱。图形中由上至下的四条曲线分别代表了SF估计的厂商效率均值、模拟样本中厂商真实技术效率的均值、最小二乘残差项出现正偏度的频率以及残差项的偏度均值。

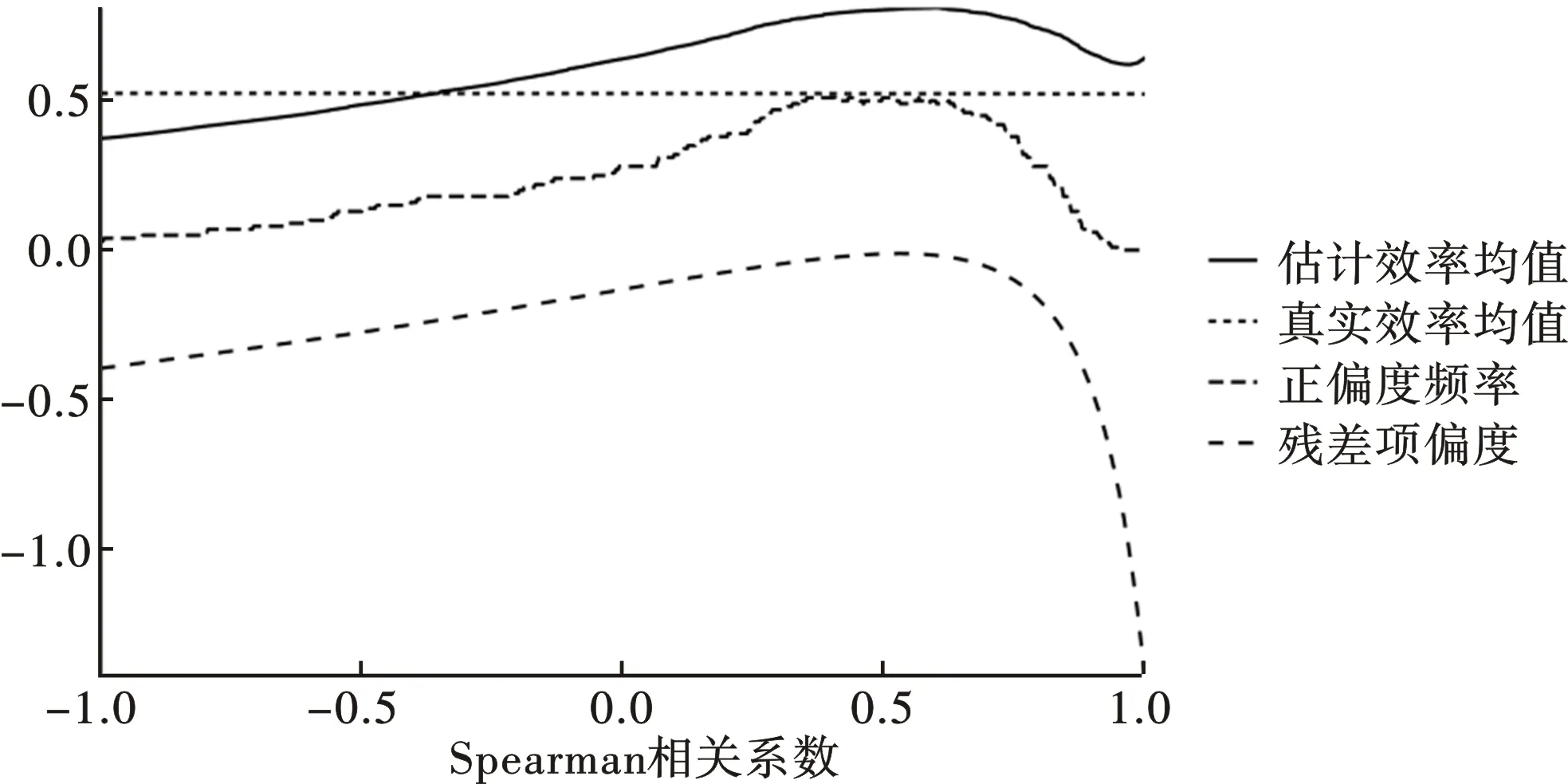
图1 样本量为50时,随机扰动项相关性对正偏度问题的影响

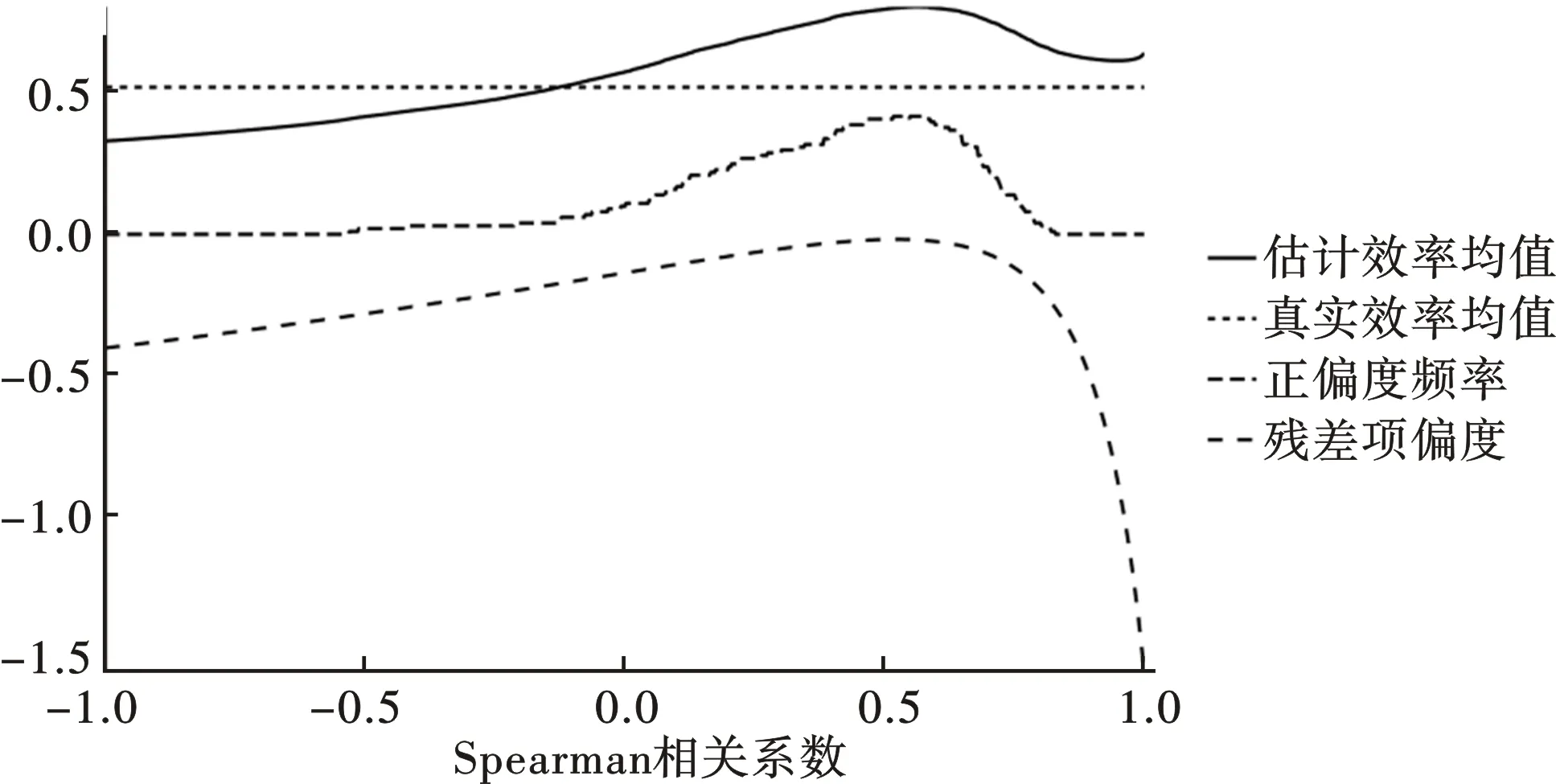
图2 样本量为500时,随机扰动项对正偏度问题的影响

厂商的真实技术效率均值仅与技术无效率项服从的总体分布有关,在模拟实验中半正态分布的参数被设置为固定值,使得技术效率平均值为常数,在图形上表现为一条水平横直线。SF估计出来的厂商效率均值与厂商的真实效率均值接近但并不重合,在两部分随机扰动项时存在较大程度的负相关时,SF会低估厂商的技术效率水平,除此以外,均存在着不同程度的高估。小样本情形下,即便Spearman相关系数取值为0,代表SF正确地设定了总体回归方程,模型对于厂商技术效率的估计依然存在向上的偏误,随着样本量的逐渐增加,这种偏误会逐渐减小。但如果模型中两部分随机扰动项存在相关性,SF对于厂商平均技术效率的估计始终有偏。

小样本情形下,模拟样本残差项的平均偏度与Spearman相关系数之间存在倒U型非线性关系,平均偏度会在Spearman相关系数的取值在0.5左右时到达峰值,尽管此时的平均偏度仍小于零,但样本残差项出现正偏度的频率到达峰值,数值在50%左右,意味着经典随机前沿模型将有一半的概率会失效。大样本情形下,两部分随机扰动项之间存在负相关时,出现正偏度的频率会大幅降低,接近于零;两部分随机扰动项之间存在正相关时,出现正偏度的频率要低于小样本情形下的频率,但依然接近40%,依然有较大的概率出现正偏度问题,进而造成对技术效率的高估。

综上所述,扩大样本量可以降低出现正偏度问题的概率,这和Waldman的研究结论保持一致,认为正偏度问题是小样本问题[3]。但在实际的研究中,样本量往往是相对固定、难以扩充的。此外,如果模型的两部分随机扰动项之间存在中等程度的正相关,即便扩充了样本量,经典随机前沿模型仍有较大概率出现正偏度问题,故而有必要通过拓展模型设定的方式来解决这一问题。

表1展示的是θ=0时的参数估计精度,此时两部分随机扰动项之间不存在相关性,经典的随机前沿模型是正确的模型设定,NC和FC则假设两者之间存在相关性。从表中结果能够看出,SF估计量的偏差、标准差与均方误差最大,尤其是对技术无效率项的分布参数σu的估计偏误较大,这与第一部分蒙特卡洛实验的结论保持一致,认为SF方法在实际应用中会存在一些问题,尤其是在小样本情形下。比较NC和FC可以看出,在样本量较小的情形下,NC估计量的估计精度并不一定高于FC估计量,这可能是因为NC的模型设定要比FC更复杂,参数估计的稳定性要稍差一些。大样本情形下,NC估计量的估计精度要显著高于FC。由此可知,使用Copula函数来刻画随机扰动项之间的相关性能够带来更精确的参数估计值,即便所选择的刻画方式并不吻合数据生成过程,有充分的理由使用Copula函数来刻画随机扰动项之间的相关性。比较不同样本情形下,各个估计量的偏差、标准差与均方误差的变化情况,可以发现,这些估计方法相应估计量的估计精度都随样本量的增加而提升,具有良好的大样本性质。

表2展示的是θ=0.5时的参数估计精度,此时两部分随机扰动项之间存在中等程度的相关性,SF的模型设定不再正确,相应估计量的估计精度最差,认为SF并不适用于此类模型的估计。比较NC和FC可以看出,NC估计量的估计精度总体上高于FC估计量,大样本情形下的对比要更为明显。与θ=0时的参数估计精度对比,发现存在中等程度相关性情形下的NC估计量的偏差、标准差和均方误差都变小了,说明估计精度变得更高了。比较不同样本情形下,各个估计量的偏差、标准差与均方误差的变化情况,可以发现,NC和FC估计量的估计精度都随样本量的增加而提升,具有良好的大样本性质,SF则存在着显著的偏误,尤其是对于技术无效率项的分布参数σu而言。

表3展示的是θ=0.9时的参数估计精度,此时两部分随机扰动项之间存在较高程度的相关性。总体上来看,SF依然具有最差的估计精度,NC具有最高的估计精度,FC则次之。与θ=0.5时的估计结果对比,发现随两部分随机扰动项之间相关性的增强,NC和FC估计量的估计精度会进一步提高。比较不同样本情形下,各个估计量的偏差、标准差与均方误差的变化情况,可以发现,NC和FC估计量的估计精度都在随样本量的增加而提升,具有良好的大样本性质。而SF关于σv的估计在大样本下依然存在着显著的偏误,结合表2的模拟结果,认为两部分随机扰动项之间存在相关性会导致SF失效。

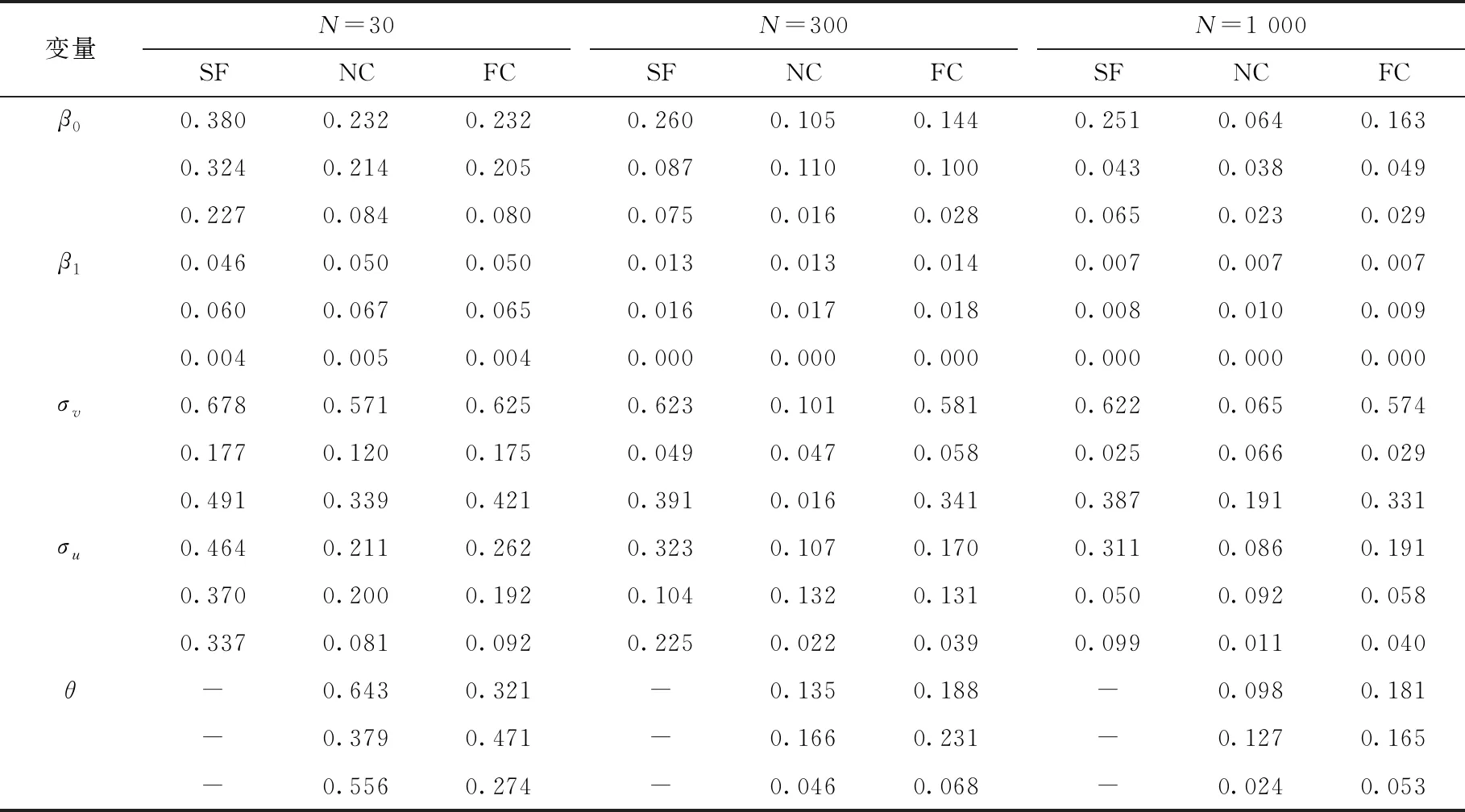
表3 θ=0.5时,三种估计方法的参数估计精度

测度厂商的技术效率是随机前沿模型的核心,进一步评估本文所提出估计方法的估计精度,将N=1 000时厂商技术效率估计值的均方误差以箱线图的形式汇总在图3中,由左至右,分别代表了FC、NC和SF三种估计方法在θ取值为0、0.5和0.9的情形下的技术效率估计量的均方误差箱线图。

从图3中能够看出,当θ取值为0,即随机扰动项之间不存在相关性时,SF是正确的模型设定,其对应的箱线图位置最低,箱宽最窄且全距最小,但拖尾严重,说明其具有较高的估计精度,但仍有可能会错估厂商的技术效率。当随机扰动项之间存在中等程度的相关性时,SF对于厂商技术效率的估计精度急剧下降,NC和FC估计量的估计精度则有所提升,总体而言要优于SF估计量。正确地设定了Copula函数形式的NC估计量具有更低的位置、更窄的箱宽及更小的全距,表明其具有更高的估计精度。当θ=0.9时,两部分扰动项之间存在着较高程度的相关性,NC估计量具有最高的估计精度,FC估计量的估计精度次之,但差距不大。综上所述,除非有较大把握认为随机扰动项之间不存在相关性,否则基于Copula方法估计随机前沿模型总能获得一些估计精度上的提升,且相关性越大,带来的估计精度提升越大。

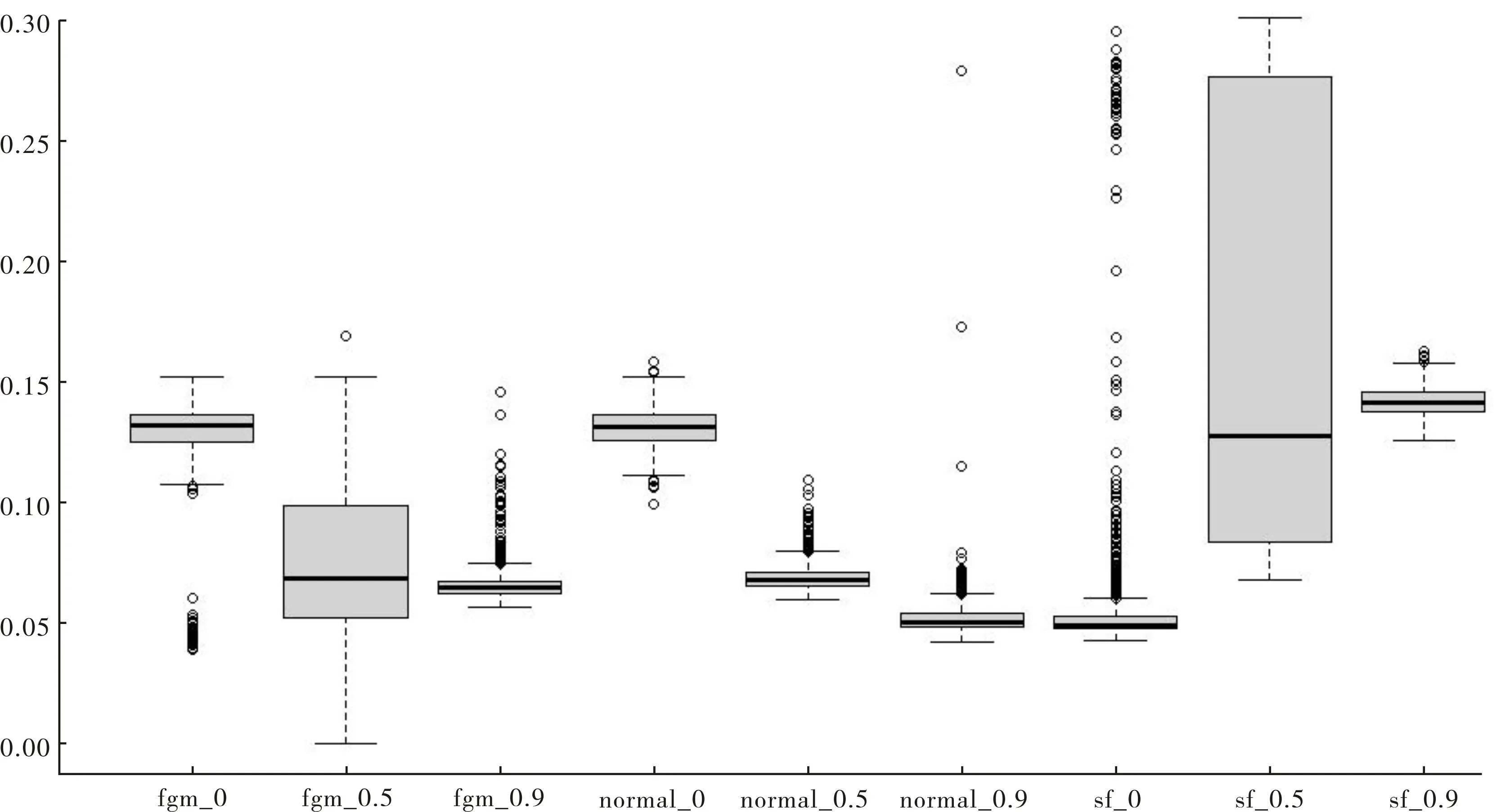
图3 厂商技术效率估计量的均方误差箱线图

四、应用分析

上市公司的技术效率历来都是学者们关注的热门话题,正确地测度其技术效率是其中不可或缺的一环。本文从Wind金融终端中收集了2018年中国沪深股市所有A股的部分年报数据,构建了如下形式的随机前沿模型:

ln revenuei=ln capitali+ln labori+vi-ui

(11)

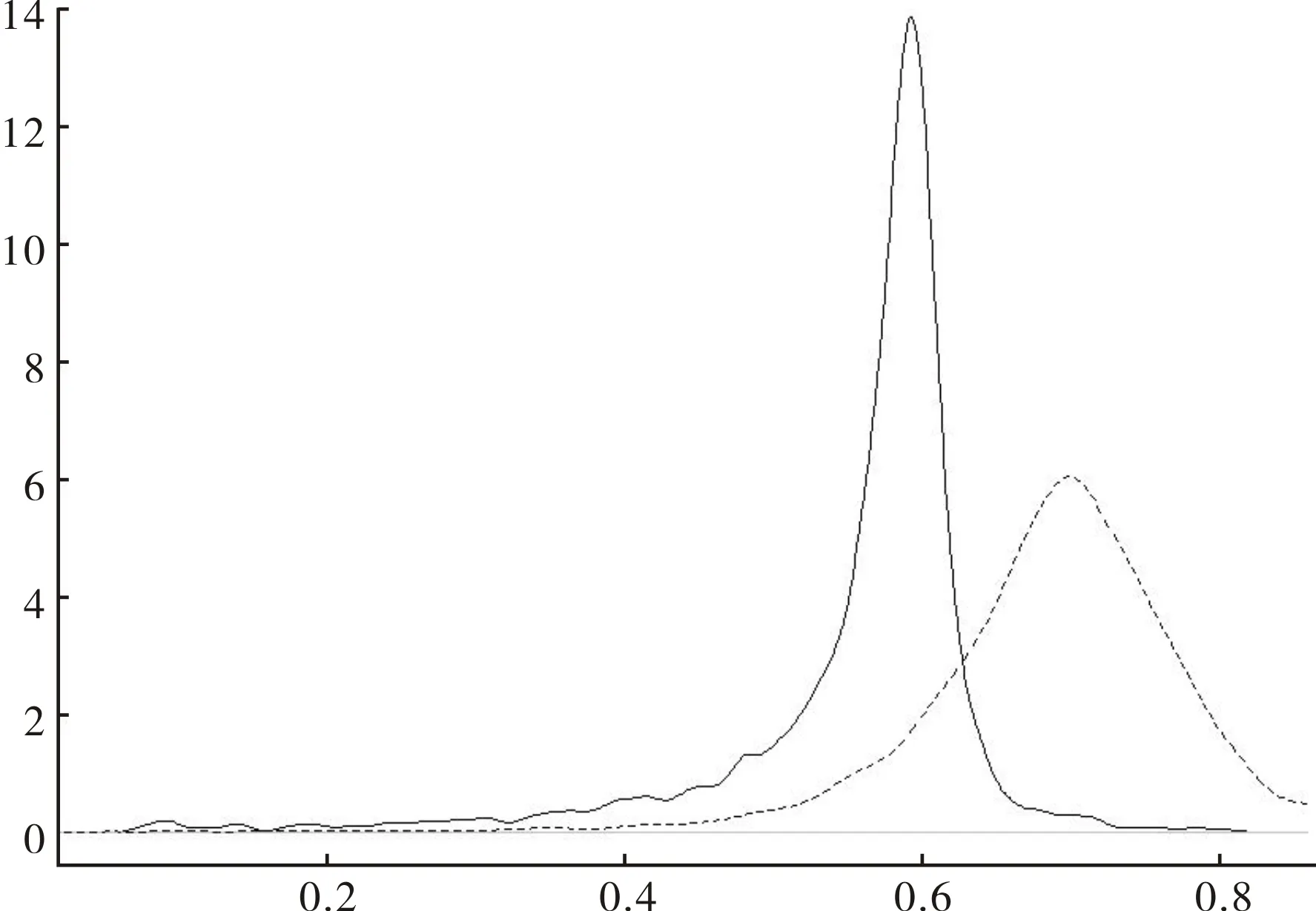
——AMH估计量,------SF估计量图4 技术效率估计值的核密度图

式(11)中的i=1,2,…,N,N代表样本容量,revenuei代表第i家上市公司的主营业务收入,capitali代表上市公司的资本投入,由上市公司的固定资产净额加流动资产合计计算得出,labori代表上市公司的劳动力投入,使用员工人数加以度量。vi和ui则分别代表了随机前沿模型的白噪声项和技术无效率项。去掉数据集中存在数据缺失的上市公司,将处理后数据的描述性统计汇报在表4当中。

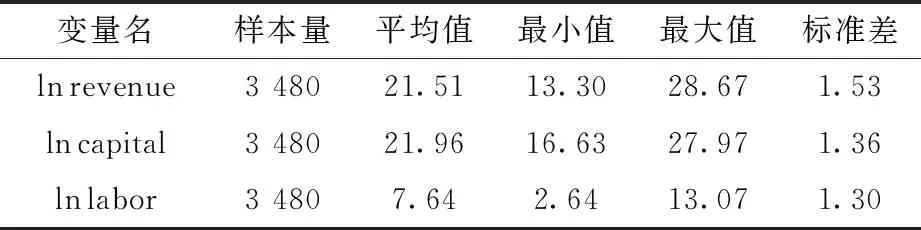
表4 对数变量的描述性统计

除前文已经提及的SF、NC和FC以外,本文还额外选择了AMH Copula和Frank Copula来刻画随机扰动项之间的相关性,将相应的估计结果汇总在表5当中。不难看出,AMH估计量具有最小的AIC,其参数θ与相应的Spearman相关系数能够通过显著性检验,表明上市公司的两部分随机扰动项之间存在正相关关系,即来自厂商控制之外的环境冲击会影响企业的技术效率,进而造成经典随机前沿模型的不适用,基于此技术效率估计值的研究结果将不再可靠。

为进一步考察两部分扰动项之间的相关性给测度上市公司的技术效率带来的影响,将由SF和AMH估计出的厂商技术效率的核密度图绘制在图4中。从图中不难看出,SF较之AMH估计量具有更大的众数与均值,倾向于高估企业的技术效率,可能会对基于此技术效率估计值的后续研究造成不良影响。

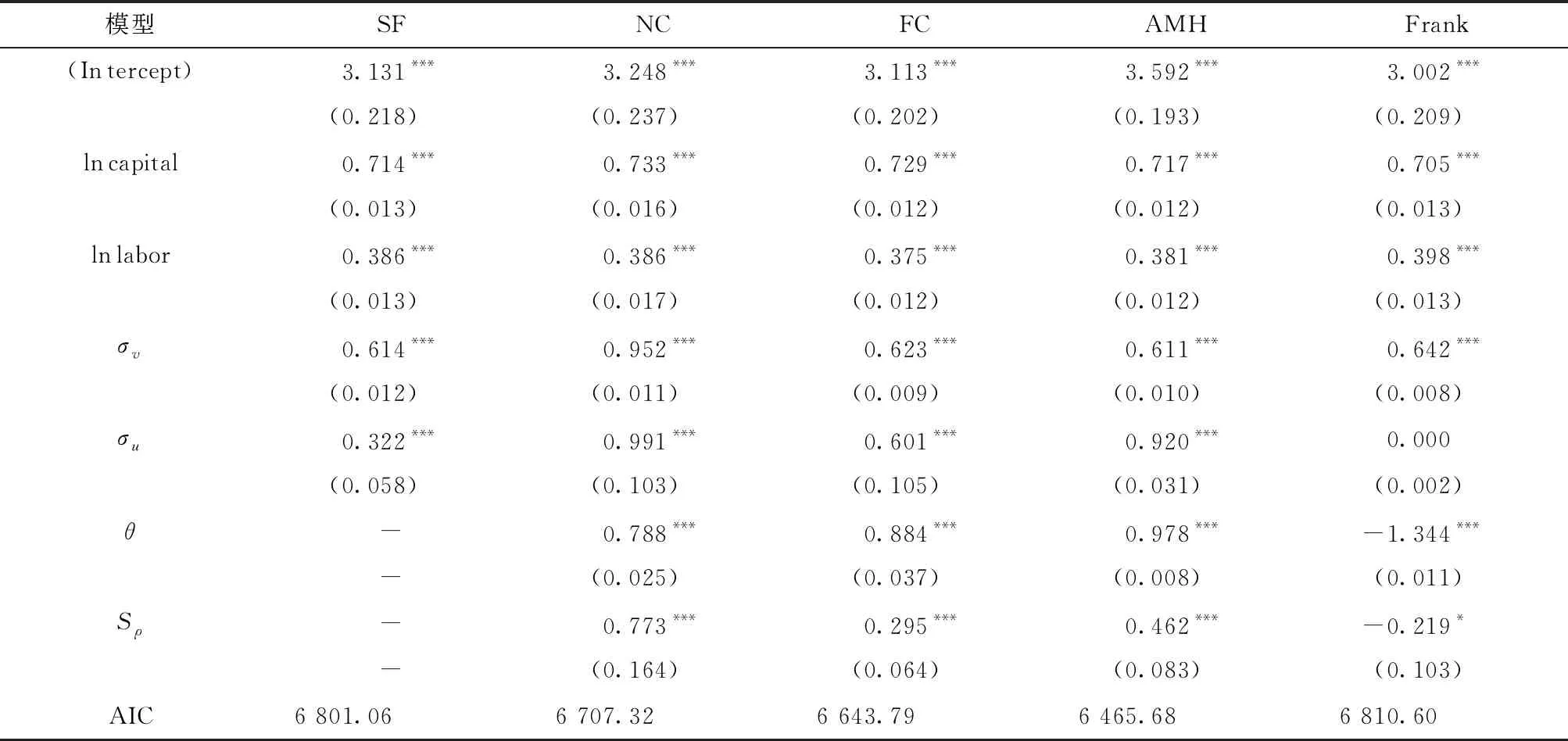
表5 2018年上市公司数据的模型参数估计结果

五、结 论

正偏度问题的存在使得经典的随机前沿模型无法给出合理的厂商技术效率估计值,可以通过修改模型设定,允许两部分随机扰动项之间存在相关性以规避该问题。本文使用Copula方法刻画了随机扰动项之间的相关性,基于极大模拟似然估计法给出了模型参数的估计量及厂商技术效率的最优预测值。蒙特卡洛实验证明:经典的随机前沿模型在样本量较小,或两部分随机扰动项之间存在相关性的情形下表现不佳,有较大概率产生正偏度问题;使用Copula函数刻画扰动项之间的相关性可以提高模型参数和厂商技术效率的估计精度,随相关性的增强,估计精度的提高会更显著;本文所提出估计方法具有良好的大样本性质,估计精度会随样本容量的扩充而提高。

本文的实例研究表明上市公司的技术效率会受到外部冲击的影响,经典的随机前沿模型会高估它们的技术效率,不应忽视随机扰动项之间可能存在的相关性。