基于超分辨率时延估计方法在室内定位应用研究*

陈 林，杨 波，徐慧俊

（京信网络系统股份有限公司，广东 广州 510663）

0 引言

随着移动通信技术的飞速发展，用户在满足基本语音业务的同时，对数据业务的需求不断提升，而用户业务场景大部分发生在室内，5G 网络的大带宽、低时延、广连接为室内业务提供必要的网络基础，推动室内业务的不断丰富。室内作为业务的主要应用场所，其网络完善成熟发展是未来5G 网络决胜的关键。室内应用多样化，网络需满足业务对网络移动性、定位能力等诉求，目前室内业务发展遇到的挑战如下[1]：

（1）场景的复杂性；

（2）商业化室内应用的智能化需求；

（3）新业态、新经济对室内数据的需求；

（4）室内数据更新；

（5）室内定位精度提升。

在室内定位应用中，大部分为商业应用，在定位系统选择上要兼顾定位精度与定位系统的商业成本的平衡，所以很多场景下不可能选择高精度的昂贵系统，需要考虑提升定位精度。传统的4G 网络虽然拥有通信体制下的定位标准技术方案，使其信号具有了定位功能，但是其实际定位精度普遍在10m 以上，无法满足用户定位精度要求。5G 的毫米波技术可获得更高精度的波达方向（Direction of arrival，DOA），比4G 更大的带宽又使其可获得更高精度的到达时间差(Time difference of arrival，TDOA)，同时5G 室内布设的密集小型基站网络使得5G 成为提高定位精度和鲁棒性的非常合适的选择[2]。

在3GPP R16 冻结版本38.305-g20[3]标准协议中，提出以下几种基于5G 信号的定位方法：

（1）基于NR 信号的NR 增强小区号法（NR E-CID）；

（2）多个环回时间（Round Trip）定位（基于NR 信号的多RTT）；

（3）基于NR 信号的下行出发角（DL-AoD）;

（4）基于NR信号的下行到达时差（DL-TDOA）；

（5）基于NR信号的上行到达时差（UL-TDOA）；

（6）基于NR 信号的上行到达角（UL-AoA）包括到达方位角（A-AoA）和达天顶角（Z-AoA）

其中，NR 信号的上行/下行到达时差估计方法，通过上行SRS（Sounding Reference Signal）或者下行PRS（Position Reference Signal）信号进行信道估计，获取终端与各个基站之间的无线信号空间传播时延，从而等效计算出终端与各个基站之间空间位置的距离，利用终端与三个基站之间的距离可以准确定位出UE 的实际位置。该类方法的定位精度主要受限于空间传播时延估计精度，在4G 网络中，20MHz 带宽基带信号的采样率为30.72MHz，时延精度偏差大约为±0.5Ts（1 个采样点持续时间约32ns），定位精度约±4.8m；在5G 网络中，100MHz 带宽基带信号的采样率为122.88MHz，1 个采样点持续时间约8ns，定位精度进一步提升至±1.2m。为了进一步提高NR 信号的定位精度，满足支持更丰富室内定位应用场景，本文重点研究基于超分辨率时延估计方法，使得时延估计准确度能够达到小于1Ts 精度，定位精度进一步获得提升。

本文首先介绍了室内多径信道的时延传播信号模型。然后介绍两种主要超分辨率时延估计算法，并对比分析算法实现流程和算法复杂度。最后，通过仿真分析验证两种超分辨率时延估计算法在室内定位精度水平。

1 信号模型

以上行参考信号SRS 为例，在NR 系统发射机中，上行SRS 信号生成后映射到对应子载波上，N点频域数据利用IFFT 实现多载波调制，然后插入循环前缀，发射时域信号x(n)可表示为：

式中，S(m)代表第m个子载波传输SRS 信号的复符号，N代表系统带宽内总的子载波数。发送信号与时变信道冲激响应进行卷积运算，在接收机中，接收信号y(n)可表示为：

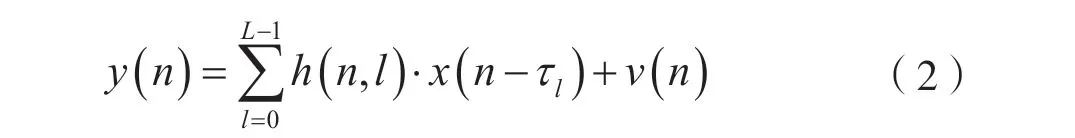
式中，h(n,l)代表第n个采样时刻第l径信道的衰落系数，τl代表第l径的传输迟延，v(n)代表第n个采样时刻信道输入复高斯白噪声，其均值为零，方差为0为首径信号的传播延迟。

接收机接收到信号y(n)，在移出循环前缀后，进行N点FFT 运算得到第k个子载波接收信号Y(k)可表示为：

式（3）可进一步表示为：

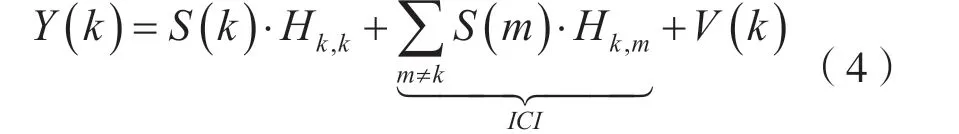
式中，Hk,m代表频域传输矩阵H的第k行第m列元素，其计算公式为：

式中，Uk(n)代表第n个采样时刻第k个子载波处的瞬时频率响应，Uk(n)计算公式为：

式（5）中，Hk,k可进一步表示为：

式（7）表明，Hk,k为Uk(n)的时间平均。式（4）可进一步表示为矩阵形式：

式中，Y代表频率接收信号矢量，H代表频域传输矩阵，S代表SRS 信号发射符号矢量，V代表信道输入复高斯白噪声矢量，频域传输矩阵H的矩阵形式为：

注意：当信道为时不变信道或者慢衰落信道时，频率信道矩阵H呈现为对角阵；当信道为快速时变信道时，频率信道矩阵H不再呈现为对角阵，非对角线元素表现为子载波间的干扰。由于室内UE 都是处于低速运动的物体，多普勒频偏可以忽略不计，因此无线信道环境为时不变信道，频域信道矩阵H呈现对角阵形式为：

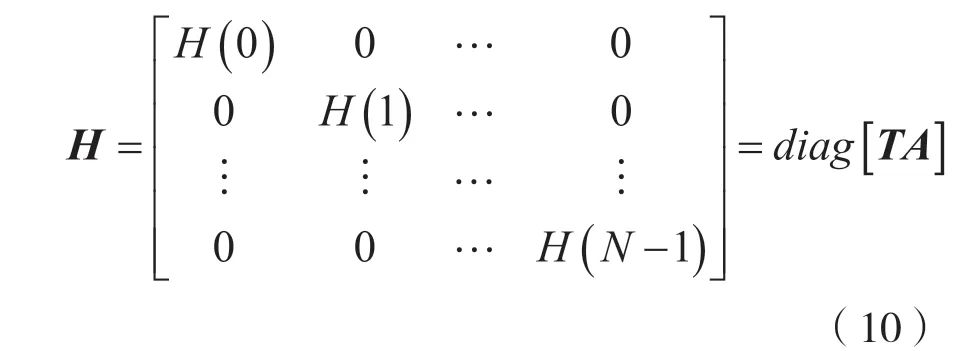
时延估计即通过从信道估计信号H(k)中提取获得主径时延信息τ0。由上述分析可知，信号通过不同路径到达接收端产生的幅度和时延信息是相互独立的[4]。

2 超分辨率时延估计算法

2.1 MUSIC 算法

根据第2 小节的分析，利用SRS 信号进行信道估计获取的频域响应为，根据公式(10)，其矩阵表示形式为T·A，

式中，T=[t(τ0),…,s(τi),…,t(τL-1)]，且t(τi)=[1,e-j2πΔfτi,…,e-j2π(N-1)Δfτi]T，A=[a0,…,ai,…,aL-1]T，al,l=0,1,…,L-1。

则频域响应的自相关矩阵RHH表示为：

对RHH进行奇异值分解，可得：

式中，Λ=diag[λ1,λ2,…,λK]，且λ1≥λ2≥…≥λL-1≥λL=λL+1=…λL=σ2。

将前面总共L个较大的特征值所对应的左右奇异矢量记为U1和V1，U1和V1对应信号子空间为Tsignal；后K-L个较小的特征值对应的奇异值矢量记为U2和V2，U2和V2对应的噪声子空间为Tnoise，其中Tsignal和t(τ1)是等价的。由于算法估计中不知道多径数，因此无法获取L的具体值。若采用算法估计L，在噪声较大的时候，估计得很不准确，由于获取信道响应对应子载波数K值较大，且多径数目不大于12 的情况下，可以将L设置为12。

由SVD 分解的原理可知，Tnoise中的任意向量均与Tsignal正交，即 ∀ui∈U2(∀vi∈V2)，有THui=0，进而所以τk必须满足：

τk满足式(14)，则必定位于fmusic的峰值点上，所以只需在τk轴上搜索，找出fmusic各峰值处所对应的τk作为各条路径的到达时刻估计。

MUSIC 算法的实现步骤如下：

（1）构造多径信号S=[s(τ0),s(τ1),…,s(τM-1)]；

（2）用每个用户的频域冲击响应H来计算协方差矩阵RHH；

（3）对RHH进行奇异值分解，得到噪声子空间U；

（4）用多径信号S与噪声子空间U来计算fmusic，并寻找fmusic的第一个峰值，就是首径时延估算值。

MUSIC 算法理论上具有任意分辨率，但实际考虑频域响应相关矩阵RHH功率谱的分布情况进行判断。为了获得更为准确的RHH功率谱，可以采用以下两方面优化[5-7]：

（1）观测数据的样本个数选取。

由MUSIC 算法的原理可知，若想估计出多径信道的多条径，就必须要有多组观测数据，因为若观测数据的个数小于多径数，则公式(15)的有用特征值个数就小于多径数，就不能估计出全部的多径时延。假设观测数据有Q组，则自相关矩阵为：

式中Q要大于多径数，且Q的值越大，估计精度越高。

（2）观测数据平滑。

由于实时性的要求，获得的观测数据是有限的，可以通过数据平滑的方法来提高样本数量，具体平滑方法如下：假设观测数据为H=[H(0),H(1),…,H(N-1)]T，可以将长度为N的观测数据分成M段，每段数据长度为R，然后利用下式进行估计：

式中M=N-R+1，Hi´=[H(i),H(i+1),…,H(i+R-1)]，i=0,1,…,L-R。

为了保证RHH是非奇异的，需要保证N-R+1＞R，R＞L，L是多径数。

2.2 MP（Matric Pencil）算法

根据公式(10)可知，接收机利用已知的SRS 信号，通过最小二乘（Least Squares,LS）信道估计算法获得信道频域响应H^(n)：

式中，n代表第n个子载波序号，n=0,1,…,N-1；N代表总子载波个数，Δf代表子载波的频带宽度，V^(n)代表最小二乘信道估计的频域上的高斯白噪声。

接下来给出MP 算法[8-11]实现步骤如下：

（1）构造频域响应矩阵Qss：

式中，Np代表频域信道估计获得采样点数，且Np＞＞L，P代表MP 算法参数，为保证最优性能，建议P取值范围Np/3 ≤P≤2Np/3。

（2）根据Nss次快拍，构造频域响应的自相关矩阵统计值

首先，计算频域响应的自相关矩阵

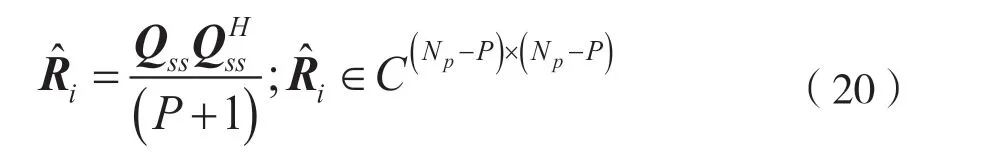
然后，对自相关矩阵进行前后向平滑：

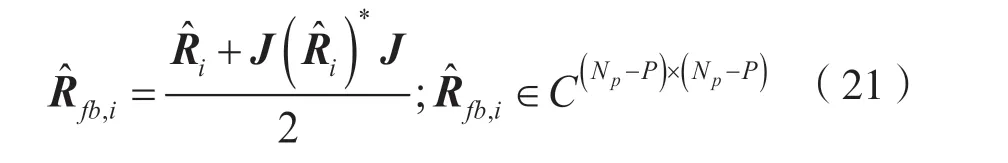
最后，得到Nss次快拍的自相关矩阵统计值

通过前后向平滑和时域平均的方式，可以减小噪声对时延估计性能的影响。

（3）计算相位矩阵Φnew：

（4）对相位矩阵Φnew特征值分解，计算得到时延值：

式中，vl,new代表相位矩阵Φnew的非零特征值，则时延τl,new：

式中，M代表Qss矩阵构造时前后两个信道频域响应的子载波索引差值，由于SRS 是间隔一个RE 进行子载波映射，因此M=2。

3 算法实现流程和复杂度分析

3.1 算法实现流程设计

第2.1 小节和第2.2 小节分别提出MUSIC 和MP 算法对SRS 信号进行时延估计。由于SRS 信号在相同的频段上可以复用多个用户，因此需要将多个用户的SRS 信号进行分离，再采用MUSIC 和MP算法进行时延估计。

假设采用MUSIC 和MP 算法进行时延估计的观测数据设置为Q，则实现中采用MUSIC 和MP 算法进行时延估计的具体流程分别如图1 所示。依次按照图1 流程对每个用户进行时延估计，可以看出MUSIC 和MP 均采用各个用户信道估计结果对每个用户时延分别进行估计。

图1 MUSIC 和MP 算法实现流程框图对比

由于MUSIC 和MP 算法要求时延估计精度小于1Ts，采样点的分辨率可达到1/2Ts 甚至1/4Ts，需要对基带仿真信号进行过采样处理获得更高的时延分辨率延迟信号。图2 给出超分辨率时延估计的仿真流程设计。

3.2 算法复杂度对比分析

假设观测数据为Q个，每个观测数据占用L个子载波。以下都以单用户、单接收天线分析MUSIC和MP 算法的复杂度。子载波L=96（用户占用16RB），MUSIC 算法采用数据平滑算法，每段数据长度为R=70，则一个观测数据可以分成27 段，MUSIC 算法的时延估计范围设置为[-10Ts,10Ts]，时延间隔为1/8Ts，则一共有161 个多径时延需要尝试估计；MP 算法的P值设置为64。表1 给出MUSIC 和MP 算法的复杂度对比。

图2 超分辨率时延估计的仿真流程设计

表1 MUSIC 和MP 算法复杂度对比

从表1 中可以看出，MUSIC 算法的复杂度要高于MP 算法的复杂度，主要是因为MUSIC 算法的复杂度与估计搜索时延范围和时延精度有很大的关系，要求估计精度越高，MUSIC 算法实现运算量就越大，而MP 算法相比较MUSIC 算法实现更为简单。

4 仿真结果与分析

本文仿真条件如表2 所示：

表2 仿真基本参数设置

分别统计在不同SNR 情况下，当CCDF 概率为0.9 时，仿真两种算法估计的时延偏差值（单位Ts，1Ts=8ns），如下图3 所示：

图3 MUSCI 算法和MP 算法仿真性能对比

观察对比图3 给出的MUSIC 算法和MP 算法仿真结果可知：

（1）当SNR=-10dB 时，两种算法的估计精度误差较大，均无法满足米级精度要求；

（2）当SNR=0/10/15dB 时，时延为0.25Ts 和0.75Ts 的情况下，MP 算法估计时延精度明显优于MUSIC 算法；

（3）当SNR=0/10/15dB 时，时延为0.25Ts 和0.75Ts 的情况下，MP 算法鲁棒性优于MUSIC 算法，时延估计偏差0.5Ts，可以满足亚米级定位精度要求。

综上所述，考虑算法定位精度、鲁棒性和复杂度，室内定位应用建议优选MP 算法。

5 结语

5G 室内定位解决方案从企业应用实际需求出发，满足不同的定位精度，可根据企业自身的发展决定使用对应的解决方案，从而推动企业的数字化、智能化发展。本文结合室内无线多径信道的数学模型，对比分析两种超分辨率时延估计方法的实现步骤，并对比给出详细的实现流程和复杂度分析；最后通过仿真对比分析MP 算法能够提供室内定位更高精度的性能，更好驱动室内定位业务发展，促进5G 网络赋能千行百业。