由渐近几乎负相协（AANA）随机变量序列生成的移动平均过程的中心极限定理

徐惠莲，王颖

（1.长春职业技术学院职业基础部，吉林长春130031；2.大连理工大学数学科学学院，辽宁大连116024）

1 引言及主要结果

定义1 如果对集合(1，2，…，n)的任意2个不相交的非空子集T1与T2，均有

其中，f和g是任意2个使协方差存在且对每个变元均非降（或同为对每个变元均非升）的函数，那么称X=(X1，X2，…，Xn) 为 负 相 协 （negatively associated，NA）随机向量，称 {Xn，n≥ 1}为 NA 随机变量序列。

定义2 如果存在非负序列q(n)→0(n→∞)，对任意的n，k≥ 1，均有

其中，f和g是任意2个使协方差存在且对每个变元均非降的函数，那么称{Xn，n≥1}为渐近几乎负相协 （asymptotically almost negatively associated，AANA）随机变量序列，称{q(n)，n≥1}为该序列的控制系数。

NA随机变量序列的定义可参见文献［1］，NA随机变量序列在可靠性理论、渗透性理论及多元分析中有广泛应用［2］。

AANA随机变量最早见于文献［3-4］。显然，当q(n)=0，n≥1时，AANA随机变量序列即为NA随机变量序列。但若令Xn=(1+a2n)-1/2(ηn+anηn+1)，其中，{ηn，n≥ 1}为独立同分布 N（0，1）随机变量，an≥0且 an→0，n→ ∞，易知 {Xn，n≥1}是AANA随机变量序列而非NA随机变量序列。因此AANA随机变量序列是更为广泛的包含独立随机变量序列和NA随机变量序列的相依随机变量序列。自AANA随机变量概念提出以来，概率统计学家对其性质进行了广泛研究，具体可参见文献［5-14］。文献［8］研究了AANA随机变量序列的中心极限定理，但至今尚未见由AANA随机变量序列生成的移动平均过程的中心极限定理的相关研究结果，为此，本文对其进行了研究。主要结果如下：

定理1 设{Xn，n≥1}是同分布且控制系数为{q(n)，n≥1}的AANA随机变量序列，当0＜δ＜1时，满足

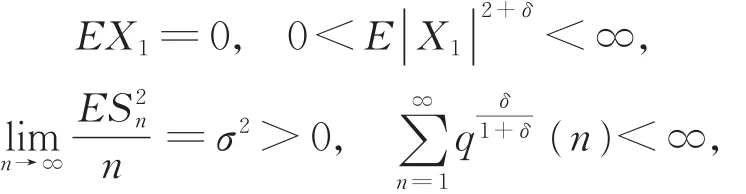
若存在严格上升的自然数序列{nk，k≥1}，当0＜α≤1时，满足

由定理1，可推出以下关于严平稳AANA随机变量序列的中心极限定理。

推论1 设{Xn，n≥1}是严平稳且控制系数为{q(n)，n≥1}的 AANA 随 机 变 量 序 列 ，当 0＜δ＜1时，满足

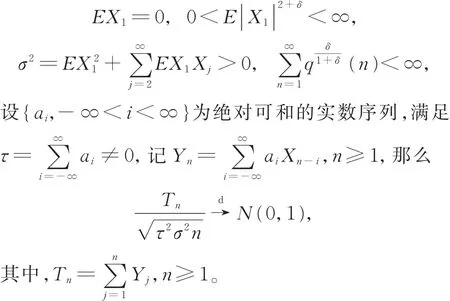
注 1 令 a0=1，ai=0，i≠ 0，显然 {ai}绝对可和且Xn=Yn，因此定理1和推论1对AANA随机变量序列的部分和也成立。本文推广了文献［8］的结果。

注2 由于AANA随机变量序列包含独立随机变量序列和NA随机变量序列，因此定理1和推论1对独立随机变量序列和NA随机变量序列仍然成立，推论1将文献［15］的结论从NA随机变量序列推广至AANA随机变量序列。

2 定理1的证明

下文中，C表示正常数，不同地方可表示不同的值。首先介绍证明中需要的几个引理。

引理 1［5］设 {Xn，n ≥ 1}是同分布且控制系数为{q(n)，n≥1}的AANA随机变量序列，满足

由引理3和Slutsky引理，可知定理1成立。

证毕！