基于动态预测的深水爆炸试验容器可靠性分析*
2021-01-26李琳娜钟东望黄小武司剑峰涂圣武
李琳娜,钟东望,黄小武,何 理,司剑峰,涂圣武
(1. 武汉科技大学理学院,湖北 武汉 430065;2. 武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉 430065;3. 江汉大学爆破工程湖北省重点实验室,湖北 武汉 430056;4. 武汉爆破有限公司,湖北 武汉 430030)
深水爆炸试验容器是一种内部填充水介质,通过加载不同的静水压力来模拟不同水深环境,基于相似原理,利用小药量进行深水爆炸理论和工程技术研究的重要试验设备。为了确保容器的使用安全,同时能够充分发挥设备的效能,有必要对其进行可靠性分析[1]。在可靠性分析方法中,目前应用最广泛的是概率可靠性分析。但对于现役深水爆炸试验容器,由于容器承受水下爆炸冲击波和加载静水压力的耦合作用,无法通过解析方法得到容器的响应规律。而采用数值模拟方法,又无法动态体现容器的服役状态,并且容器的样本数据非常有限,很难获得容器抗力的概率分布。因此,采用概率方法进行深水爆炸试验容器可靠性分析实用性不强。
20 世纪90 年代以来,Ben-Haim[2]和Elishakoff 等[3]提出并倡导使用不确定性的凸集模型。郭书祥等[4-5]、孙海龙[6]提出了基于区间分析的非概率可靠性模型,所提出的区间可靠性指标具有明确的物理意义。由于结构的不确定性既可能是概率的,也可能是非概率的,同一问题中可能同时包含概率变量和非概率变量,因此混合模型的研究具有重要的实际意义。近年来,学者们[7-12]采用混合模型对同时包含随机变量和区间变量的结构进行可靠性分析,取得了很好的效果。考虑到结构在服役期间的性能退化为动态过程,杨正茂等[13]、彭兆春[14]、杨周等[15]针对随机载荷和强度退化所引起的动态可靠性问题,将载荷和强度同时考虑为随机过程,开展了结构的时变可靠性研究。
针对现役深水爆炸试验容器可靠性分析,提出一种基于智能预测的随机-区间动态可靠性模型。模型中通过对容器响应进行动态预测,将最大应变预测结果加上预测网络误差,以确定容器最大应变区间变量。与现有混合可靠性分析模型相比,本模型的区间变量随着结构动态测试数据的变化而变化,且对结构的不确定性分析也是动态的,因此得到的容器可靠性也随着其服役过程不断变化,具有动态特性,能够更好地反映容器在服役期间的性能变化,可为容器的使用维护提供决策依据。
1 随机-区间模型可靠性分析方法
1.1 随机-区间模型
在结构可靠性分析中,若其不确定性同时包含随机因素和认知因素,则可将结构中的不确定性变量处理为随机变量和区间变量,对于同时包含随机变量和区间变量的结构,所建立的模型称为随机-区间可靠性分析模型,其功能函数可以描述为:
1.2 可靠性计算

2 深水爆炸试验容器可靠性分析模型
2.1 容器结构中的随机变量
以现役10 g TNT 当量,可模拟200 m 水深的椭圆柱形深水爆炸试验容器作为研究对象,容器实际结构如图1 所示。容器主体为两端标准椭圆封头、中部圆柱直段的卧式结构。内部加载2.0 MPa 静水压时,容器可承受内部中心位置最大10 g TNT 当量爆炸载荷而不发生可见塑性变形和漏水。在日常检查、维护良好条件下,使用寿命大于15 y。容器壳体材料为16 MnR 钢,将容器材料的屈服强度及材料的弹性模量作为可靠性分析模型中的随机变量。
2.2 容器结构中的区间变量
由于深水爆炸试验容器在试验过程中同时受到加载静水压和爆炸冲击载荷的耦合作用,很难用解析方法求得最大应变。而数值模拟方法又无法准确反映容器在服役期间性能的动态变化,因此通过容器动态测试数据结合人工智能算法,进行容器响应的动态预测,通过最大应变预测结果加上预测模型误差,可得到容器最大应变区间变量的变化区间。
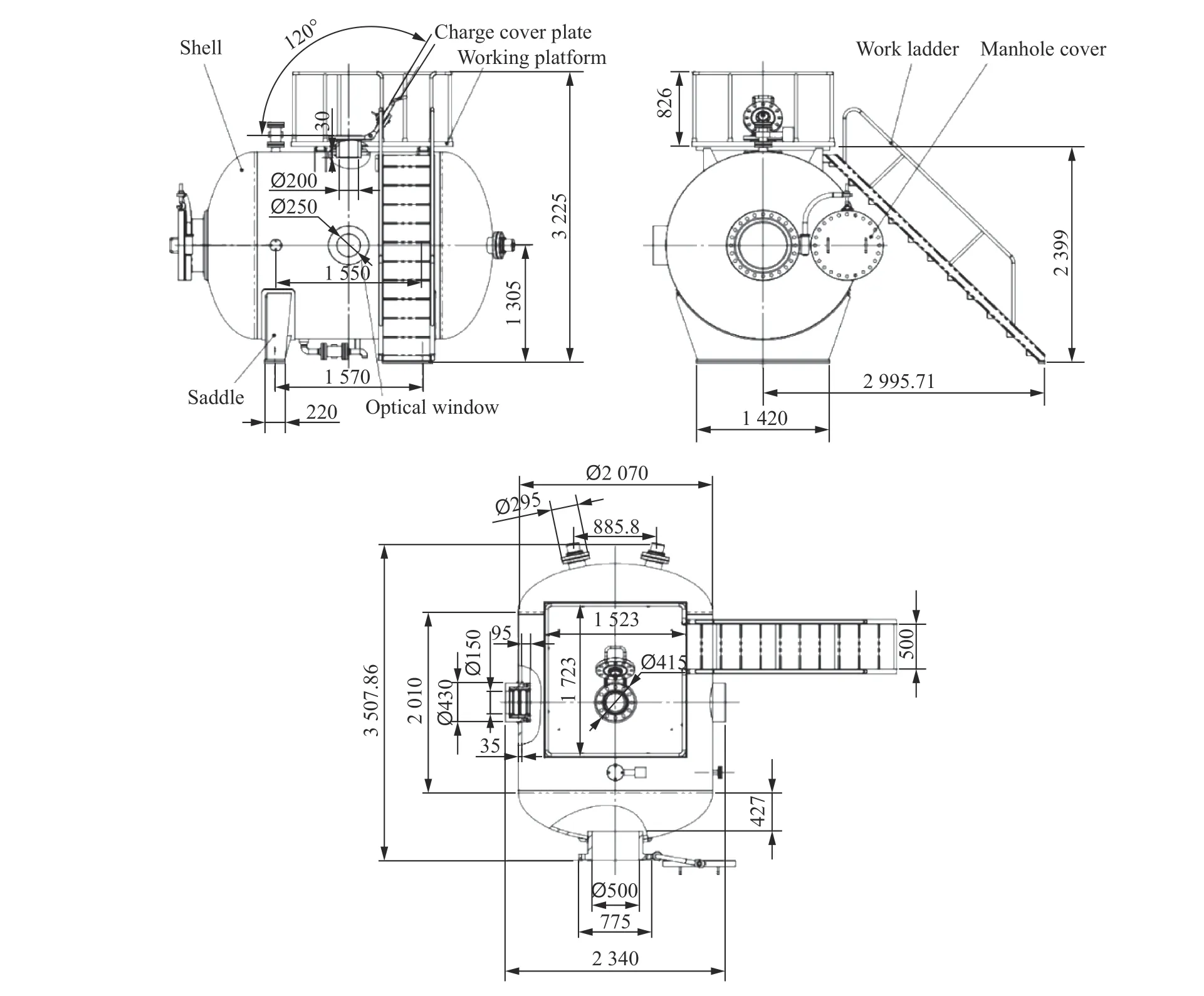
图 1 深水爆炸试验容器结构(单位: mm)Fig. 1 Structure drawing of deep-water explosion test vessel (unit: mm)
容器的最大响应一般发生在容器距离爆心最近的中环面处,但由于容器封头的汇聚作用,在容器椭球封头顶端也可能产生最大响应,因此分别在容器中环面和封头顶端处设置2 个应变测点。考虑到容器结构中鞍座、光学窗口和工作平台都位于中环面上,为了尽可能地减小其约束作用,测点1 设置在光学窗口和工作平台之间的中点位置。具体测点位置如图2 所示。
通过容器服役期间的动态应变测试数据,基于广义回归神经网络(GRNN)建立容器动态响应预测模型。GRNN 模型的输入变量为药量、加载静水压、测点位置,以容器应变作为网络输出变量,以容器服役期间31 次试验的62 组数据(见表1)训练预测模型,由于样本数量有限,采取4 折交叉验证方法训练GRNN 神经网络,并循环找到最佳的SPREAD,采用最佳方法建立GRNN 网络,计算得到预测模型在容器中环面和封头顶端两处应变预测的绝对误差。
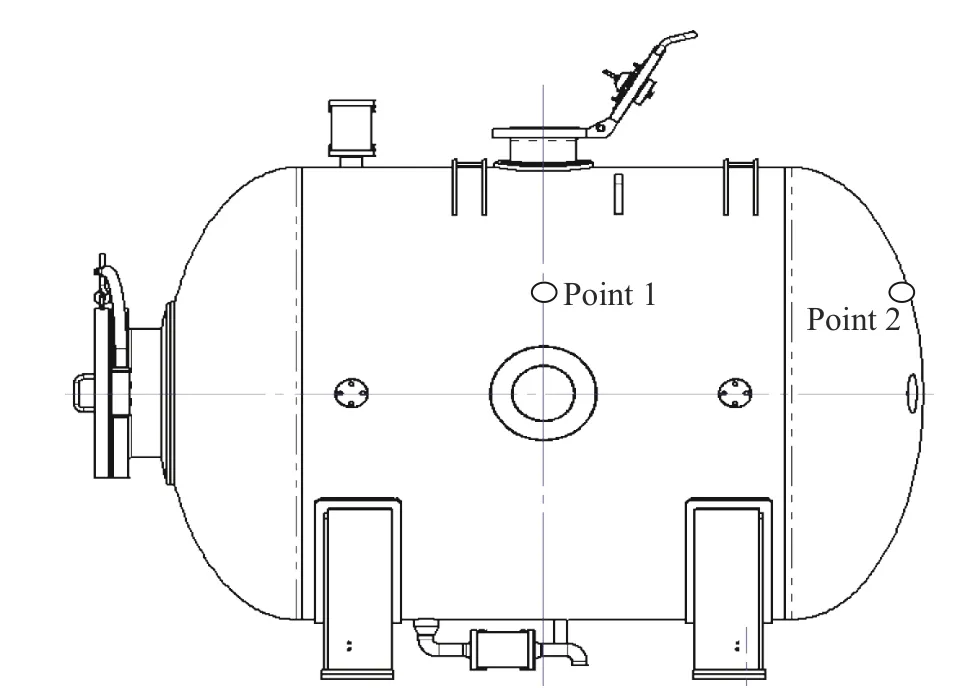
图 2 测点位置示意图Fig. 2 Schematic diagram of measuring points location
利用训练好的GRNN 网络模型对服役期内深水爆炸试验容器在极限载荷下的应变进行预测,取容器中环面和封头顶端两处应变的最大值进行比较,考虑预测模型相应位置的绝对误差,得到容器最大应变 εmax的变化区间。
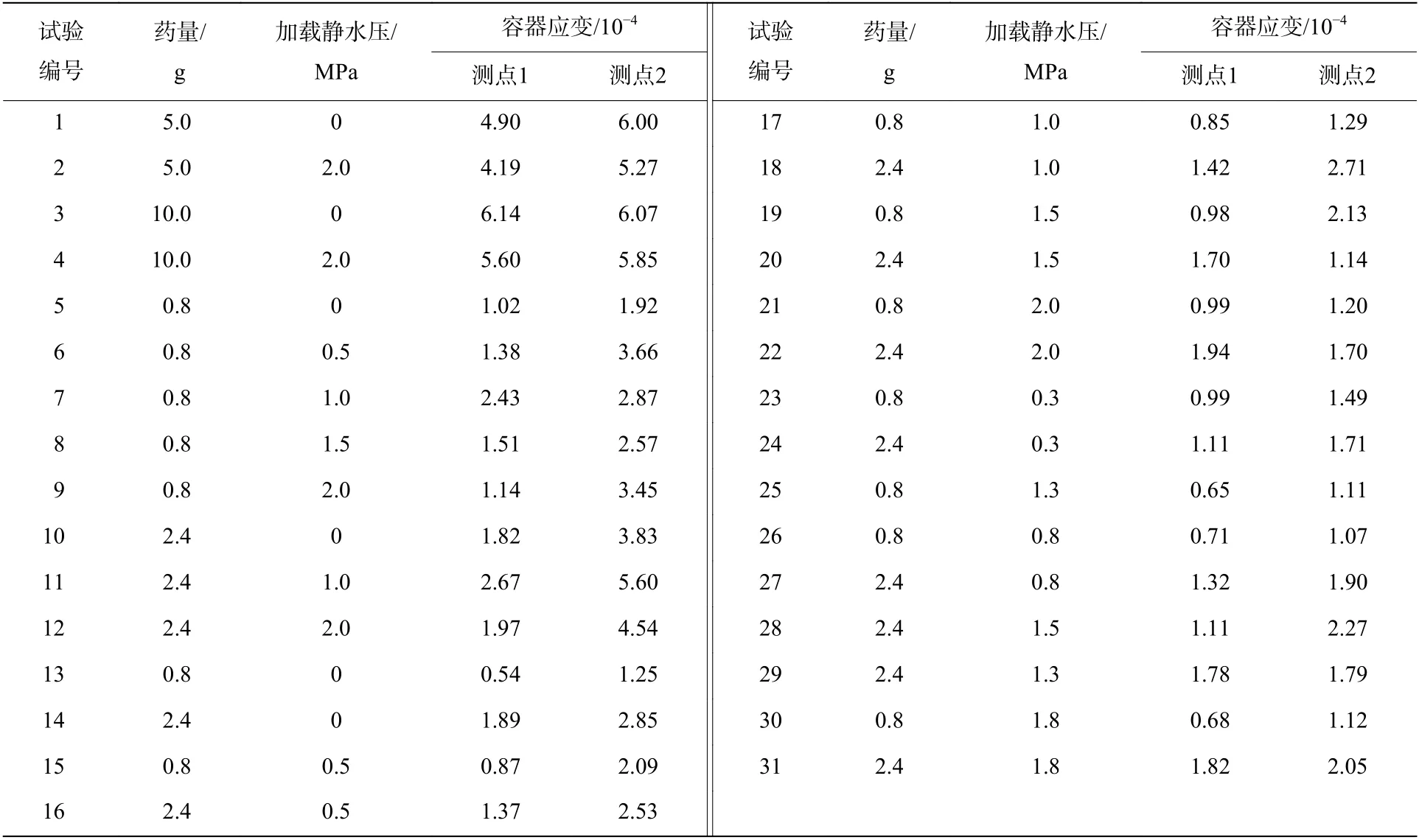
表 1 测试应变数据Table 1 Test stain data
2.3 容器的失效状态函数
深水爆炸试验容器的可靠性是指容器在设计服役期间和最大允许载荷条件下安全试验的能力。当容器在设计载荷下的最大应力超过容器材料的屈服强度极限时,认为容器失效。而容器的最大应力可由容器的最大应变乘以材料的弹性模量得到,由此可以确定深水爆炸试验容器可靠性分析的失效状态函数为:

式中: εmax为容器的最大应变区间变量,E为容器材料的弹性模量随机变量, σs为容器材料的屈服强度随机变量。
3 现役深水爆炸试验容器可靠性分析
3.1 基本参数
材料的屈服强度和弹性模量通常服从正态分布,通过查阅文献获得了16MnR 钢材料各随机变量的数字特征,随机变量分布如表2 所示。利用2.2 节中训练好的GRNN 模型进行容器第32 次试验的最大动态应变预测,得到容器在设计极限载荷下的最大应变。预测过程如图3 所示,预测结果如表3 所示。

表 2 随机变量分布Table 2 Distribution of random variables
图 3 动态应变GRNN 预测过程Fig. 3 GRNN prediction process of dynamic strain

表 3 第32 次试验预测结果Table 3 Prediction results of the 32nd test
通过对比预测结果可以看出,容器在极限载荷下的最大动态应变发生在容器的中环面处。此外,由于容器加载静压时还会产生静态应变,因此容器的应变应由动态应变和静态应变两部分构成。测试试验前,首先测量容器在加载2.0 MPa 静水压时的静态应变,得到容器在中环面和封头顶端两处的静态应变分别为2.11×10-4和3.23×10-4,由此可以确定容器在极限载荷下的最大应变发生在容器的封头顶端,并得到容器最大应变的区间变量为εmax∈ [8.38×10-4,8.62×10-4]。
3.2 容器的可靠性指标计算


式(16)中仅含有随机变量,采用蒙特卡罗法进行失效概率计算,得到容器的失效概率为零,说明容器在设计的极限载荷下是安全的。
3.3 对比分析
通过3 种方法分别对容器可靠性进行分析,计算结果如表4 所示。对比计算结果可以看出:(1)由于深水爆炸试验容器属于高可靠性结构,因此采用将区间变量等效为随机变量和二级功能函数两种方法进行可靠性计算时,只能得到失效概率为零,其可靠程度无法比较。(2)在深水爆炸试验容器混合可靠性分析过程中,由于功能函数中只包含一个区间变量,因此采用随机区间化功能函数进行区间可靠性指标计算非常简便有效。(3)对比3 种方法的计算时间可以发现,当随机变量等效为区间变量进行计算时,其计算时间仅为其他方法的10-2量级,计算效率更高。
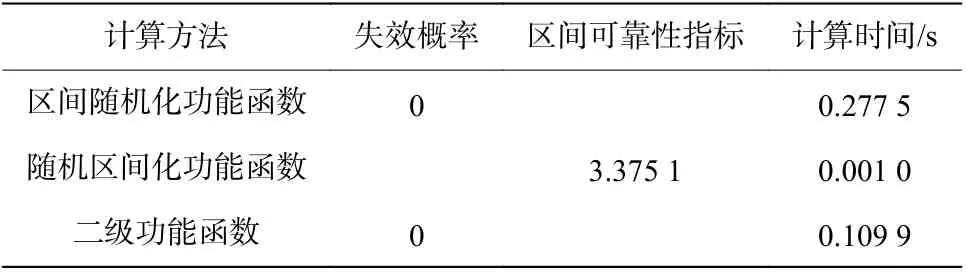
表 4 容器可靠性计算结果Table 4 Calculation results of vessel reliability
4 结 论
针对现役深水爆炸试验容器的可靠性分析,结合概率可靠性理论和区间可靠性理论,建立了随机-区间可靠性模型。通过对容器基本参数的不同处理,采用3 种方法进行了可靠性计算。通过分析,得出以下主要结论。(1)由于深水爆炸试验容器在试验过程中同时受到加载静水压和爆炸冲击载荷耦合作用,很难用解析方法求得最大应变。而数值模拟方法又无法准确反映容器在服役期间性能的动态变化,因此通过容器动态测试数据结合人工智能算法,进行容器响应的动态预测,然后在最大应变预测结果加上预测模型误差,可得到容器最大应变区间变量的变化区间。该区间具有自适应性,能反映当前容器的服役状态,为后续的动态可靠性分析奠定了基础。(2)采用基于动态响应预测的随机-区间模型进行深水爆炸试验容器可靠性分析,不仅很好地解决了在概率可靠性分析中,由于样本数据有限,参数的统计规律难以获得的缺陷,同时由于可靠性分析是基于容器在服役期间动态响应测试数据得到的区间变量,因此可靠性分析是随容器服役时间推移而动态变化的,具有动态特性,有利于进一步指导容器在服役期间的使用维护决策。(3)通过对随机-区间模型的可靠性指标计算方法进行对比发现,对于深水爆炸试验容器这类高可靠性结构,采用将随机变量等效为区间变量,然后进行区间可靠性指标计算的方法,不仅可以更直观地量化结构可靠程度,而且大大提高了计算程序运行效率。(4)基于动态预测的混合可靠性模型及区间可靠性指标计算的基础上,可以进一步构建在役深水爆炸试验容器使用维护的混合时变可靠性优化设计模型,优化方案中可以限定容器服役期内区间可靠性指标,通过调整使用过程中的最大允许载荷,实现容器服役年限的最大化。
