梯度密度黏弹性材料的波传播研究*
2021-01-26苗春贺徐松林张金咏王鹏飞
李 毅,苗春贺,徐松林,2,张金咏,王鹏飞
(1. 中国科学技术大学中国科学院材料力学行为和设计重点实验室,安徽 合肥 230027;2. 中国地震局地震预测研究所高压物理与地震科技联合实验室,北京 100036;3. 武汉理工大学材料复合新技术国家重点实验室,湖北 武汉 430070)
超结构/材料是解决复杂防护效应问题的关键之一,是一种微观异构、宏观连续的介质,表现出一些特别优异的功能和物理力学性质,例如同时兼具高强度和高韧性,在高技术领域,已经形成了分类众多的工艺和产品。梯度密度材料是近几年制作工艺逐渐成熟的一种超结构/材料,形成了生物功能梯度材料、光学功能梯度材料等,并逐渐在多种领域得到了应用。由于这种介质含有大量的多尺度的细微观结构,这些细微观结构会使得应力波产生波形弥散和衰减现象[1-2],其宏观响应均具有一定的黏弹性特征。研究冲击载荷作用下这种梯度材料的黏弹性响应特征,有助于揭示介质的细微观结构对应力波传播的影响规律,为材料的优化设计提供依据。本文中将结合分离式霍普金森压杆(SHPB)实验技术对梯度密度黏弹性材料的冲击响应进行研究。
SHPB 技术广泛应用于测量材料动态力学特性[3]。Zhao 等[4]给出了采用黏弹性波导杆时确定试件动态本构关系的方法,Bacon[5]、王宝珍等[6]采用传播系数法较系统地分析了黏弹性试件中波传播过程中的弥散和衰减规律,以及动态本构关系的测试方法;朱珏等[7]分析了试件中传播的黏弹性波对SHPB 实验过程中应力均匀性等因素的影响规律。黏弹性波的传播理论是研究波传播特性的关键[8],Ting 等[9]、Tedsco 等[10]、Han 等[11]基于波动方程的Laplace 变换方法研究了黏性层状介质中弹性波的传播特性和频率域中的等效分析方法,Mukerji[12]通过测试研究了层状介质中弹性波的衰减和弥散。这些研究对弹性波在不同的多层弹性介质中的传播规律进行了实验和理论探索,揭示了弹性波波速对材料细观结构特征的频率相关性。进一步,周风华等[13]、郑宇轩等[14]基于波动方程的Laplace 变换和数值Laplace 逆变换对SHPB 实验过程中黏弹性波的传播做了卓有成效的工作。这些研究都是针对均匀的黏弹性材料进行的,如果黏弹性材料不是均匀的,即其密度具有一定的分布特征,则会给波动分析带来较大的困难。张鸣等[15]基于Euler 方程的形式给出了垂直入射情况下梯度密度黏弹性材料中波动传播分析的一个近似解,得到了一些初步结论。
基于此,本文中将在张鸣等[15]工作的基础上,进行垂直入射情况下多层梯度密度黏弹性材料中波动传播的分析,结合梯度钛-硼化钛材料[16]和碳纤维增强树脂材料[17]进行初步实验研究。
1 冲击下多层梯度密度黏弹性介质中波的传播
1.1 控制方程和近似解
梯度密度黏弹性介质中,密度ρ 是位置x的函数,即:ρ=ρ(x)。其中的变形连续方程、动量守恒方程分别为:


1.2 垂直入射多层梯度介质中波的传播
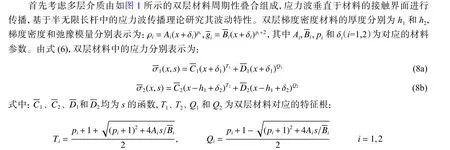
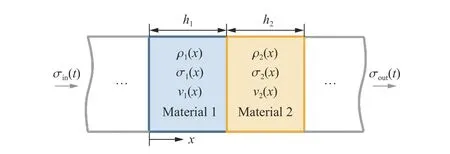
图 1 垂直入射双层周期性叠合介质示意图Fig. 1 Schematic diagram of a two-layer periodically-superimposed medium with normal incidence


2 梯度密度钛-硼化钛材料的动力学行为
2.1 材料
梯度钛-硼化钛(TiB2-TiB-Ti)陶瓷材料由武汉理工大学材料复合新技术国家重点实验室采用沉积烧结的工艺制备[16]。梯度材料的第1 层为纯钛,后续各层中逐次减少10%的钛,并以同体积的硼化钛进行填充,由此制备的样品从光亮的白色(钛)逐渐转变为暗淡的灰黑色(硼化钛),如图2 所示。随着硼化钛含量的增加,样品的硬度[16]逐渐增加,表现出较强的梯度分布特征。对3 个样品中的密度分布进行统计,沿厚度方向均匀地切取6 个直径(4±0.1) mm、厚度(1.5±0.1) mm 的圆柱体测量其密度,结果如图2 所示,随着硼化钛含量的增加,样品的密度逐渐增加。采用 ρ =A(x+δ)p对梯度密度分布进行拟合,δ 取为1.0,可得到密度递增时的参数为:A=4.45 g/cm3,p=2.0。将此样品反过来,可得到密度递减时的参数为:A=4.56 g/cm3,p=-2.45。采用相似的形式也可对梯度硬度的分布进行拟合。
应用SHPB 加载装置分别对单个试件和两个样品组合试件进行动态加载实验,以对应研究单层梯度介质与双层梯度介质中应力波的传播。实验采用了比较低的冲击速度,例如本实验中的5.0 m/s,以研究介质的黏弹性行为。单个试件尺寸为:直径(13±0.1) mm,厚度(10±0.1) mm。
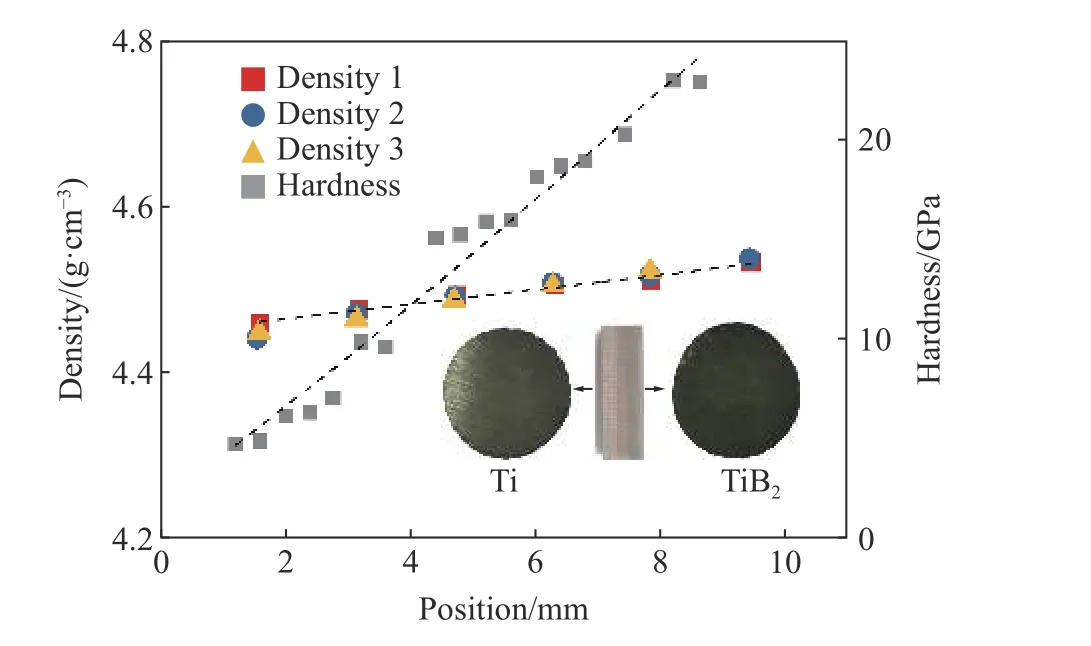
图 2 梯度钛-硼化钛样品中密度和硬度[16]分布Fig. 2 Distributions of density and hardness[16]in gradient Ti-TiB2 specimen
2.2 单层和双层梯度钛-硼化钛材料的波传播
实验中入射波信号如图3(a)所示,所有实验中基本控制不变。测得的透射信号如图3(b)所示,包含有:单层密度递增、单层密度递减、双层密度递增叠合、双层密度递减叠合、单层密度递增与单层密度递减叠合,以及单层密度递减与单层密度递增叠合等6 组实验,每组重复3~5 次。
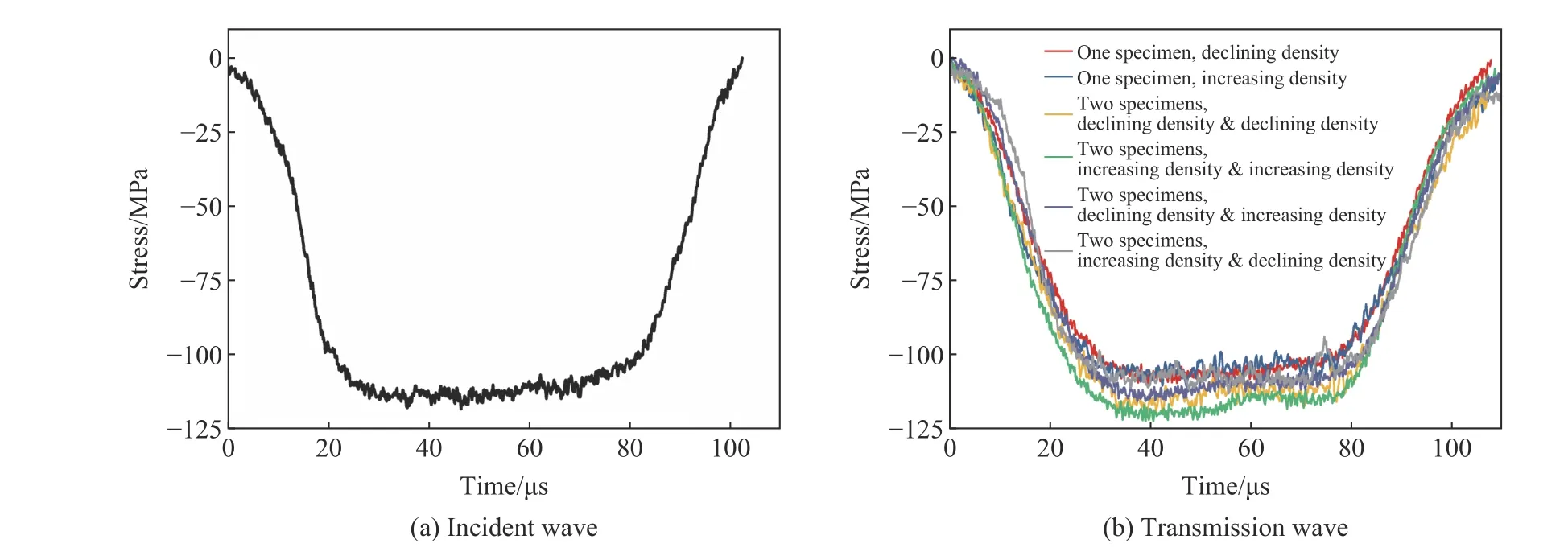
图 3 梯度钛-硼化钛实验波形Fig. 3 Recorded wave profiles in the gradient Ti-TiB2 specimens
基于上述理论分析,对于单层试件,由解的形式(6)和试件两端的入射波信号 σin(t) 、透射波信号σout(t) ,可以得到:

将不同试件的入射波信号和透射波信号代入式(16)或式(17)进行计算。由于入射波信号 σint(t) 与透射波信号 σout(t) 均为离散的数据,进行Laplace 数值逆变换计算比较麻烦,因此,为简化分析过程,对波形的加载部分均采用Asin(wt) 的形式进行拟合,然后进行Laplace 逆变换。图4 为单层试件的分析结果,其中实线为采用SHPB 实验的三波法进行处理的结果,虚线为上述理论模型计算的结果,分别进行了试件的撞击端(x=0)、支撑端(x=L),以及试件中部(x=L/2)的应力波形的计算。由此可见:(1)三个位置计算得到的应力-时间曲线有一定的差异,说明此梯度钛-硼化钛陶瓷材料中内界面的存在,使得梯度材料表现出一定的黏性,虽然还很弱;(2)计算得到的应力-时间曲线与SHPB 三波法处理得到的结果非常接近,此时反射波的波形结构比较简单,黏性对SHPB 三波法分析影响不大。
图5 为双层材料叠合试件的计算结果。实线为采用SHPB 实验的三波法进行处理的结果,虚线为计算结果,包含了试件的撞击端(x=0)、支撑端(x=2L),以及两个试件之间(x=L)的计算波形,以作对比。由此可见:三波法处理得到的结果与两个试件中部的计算结果比较接近;3 个位置计算得到的应力-时间曲线的幅值有一定的差别,且密度递减介质中随传播距离的增加,应力幅值减小的幅度相对较大。虽然单层梯度钛-硼化钛陶瓷材料中由于内界面的存在产生的黏性不是很强,但是双层密度梯度材料的叠合制造了新的宏观界面,使叠合介质整体表现出更强的黏弹性特征,这主要表现在应力幅值和应力波形的上升过程随传播距离的增加都出现了明显变化,反映出一种介质中多种微结构组成导致的黏弹性机制[12]。叠合试件的黏性使SHPB 三波法分析结果与材料的性能之间存在一定的差异。
3 碳纤维增强树脂材料的动力学行为
3.1 复合材料
碳纤维增强环氧树脂材料[17]中碳纤维粉末的型号为XGCP-300,密度为1.75 g/cm3。在环氧树脂中加入4 种质量分数(0%、10%、30%、50%)的碳纤维粉末来制备4 种密度的复合材料,制得的材料如图6 所示,随着碳纤维含量的增加,样品的密度显著增加,即从质量分数0%时密度为(1.17±0.1) g/cm3,增加到质量分数10%时密度为(1.21±0.1) g/cm3、质量分数30%时密度为(1.35±0.2) g/cm3,最后增加到质量分数50%时密度为(1.57±0.2) g/cm3。环氧树脂(碳纤维含量0%)弛豫模量为(1.20±0.1) GPa,其布洛克菲尔德黏度为800 MPa·s。随碳纤维含量增加,弛豫模量增加到质量分数为10%时的(1.24±0.1) GPa、质量分数为30%时的(1.38±0.2) GPa,最后增加到质量分数为50%时的(1.61±0.2) GPa。同时,随着碳纤维粉末含量的增加,样品由透明状逐渐变为黑色;样品的灰度统计基于试样表面显微镜拍摄图片分析处理而来,灰度分布随碳纤维含量的增加向灰度值较小的黑色区域移动,灰度分布区域随含量的增加越来越集中,样品的均匀性相对也较好。碳纤维增强环氧树脂试件表现出明显的黏性特性;但随着碳纤维含量的增加,试件显得越来越脆[17]。
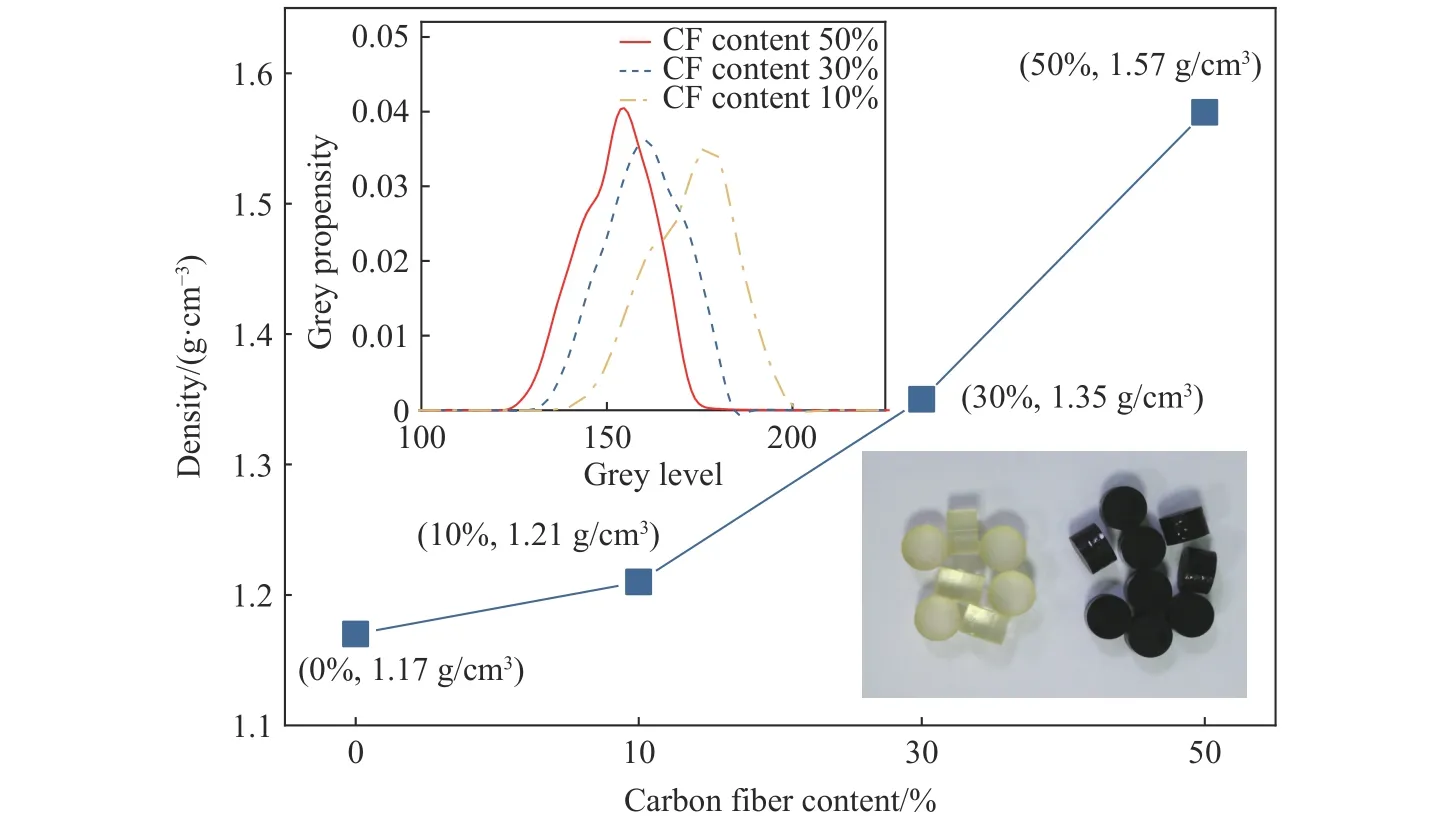
图 6 制备的碳纤维增强树脂复合材料的密度随碳纤维质量分数的变化Fig. 6 Density change of prepared carbon-fiber reinforced resin composites with carbon fiber mass fraction
梯度密度黏弹性材料的制备很困难,初始拟采用不同密度的多层黏弹性材料来叠合成梯度密度介质,但是冲击实验成功率非常低,重复性也不好。因此,将仅对双层黏弹性材料叠合介质应用SHPB 加载装置进行动态加载实验,以研究双层黏弹性介质组成的近似“梯度密度”试件中应力波的传播。实验采用比较低的冲击速度,例如5.0 m/s。单个试件尺寸为:直径(8±0.1) mm,厚度(4±0.1) mm。
3.2 双层碳纤维增强树脂材料中的波传播
图7 为双层材料叠合的近似“梯度密度”试件的计算结果。实线为SHPB 实验三波法处理的结果,以作对比;分别进行了试件的撞击端(x=0)、支撑端(x=2L),以及两个试件之间(x=L)的应力波形的计算。图7(a)、(b)、(c)所示双层叠合材料分别对应碳纤维质量分数由50%减小到30%、10%、0%;图7(d)、(e)、(f)所示双层叠合材料分别对应碳纤维质量分数由0%增加到10%、30%、50%。由此可见:三波法处理得到的结果与两个试件中部的计算结果比较接近;三个位置计算得到的应力-时间曲线的幅值有较大的差别,且随传播距离的增加,应力幅值出现较大的减小幅度,表现出比单层材料更强的黏弹性特征。这种黏性特性包含材料本身的黏性和微结构组成导致的黏性等两种机制。叠合试件的黏性使SHPB 三波法分析结果与材料的性能之间存在较大的差异:由于SHPB 三波法选取了入射杆与透射杆得到的入射波、反射波与透射波,在进行计算时,得到的是两杆之间试件应力情况的平均值。而实验所选取的材料具有变密度特性,而且对于碳纤维增强树脂材料,其两杆之间的密度变化较大,在试件的不同位置处,其应力会有一定的差距。因此采用SHPB 三波法分析得到的平均应力不能较好地反映试件密度的变化特性,也较难得到试件不同位置的应力变化情况。
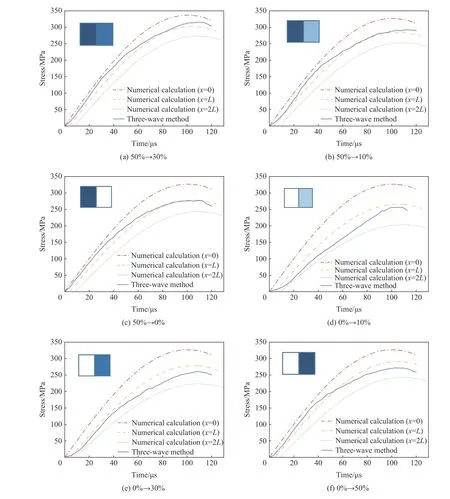
图 7 双层碳纤维增强树脂叠合试件中的应力波形Fig. 7 Stress-time curves in two-layer superimposed specimens of carbon fiber reinforced resin
将双层材料叠合的试件等效成单层等效的梯度密度黏弹性介质。首先,采用 ρ =A(x+δ)p的形式对近似梯度密度试件进行拟合,δ 取为1.0,可以得到密度递减时的参数分别为:50% → 30% 时,A=1.57 g/cm3,p=-18.95;50% → 10%时,A=1.57 g/cm3,p=-32.69;50% → 0%时,A=1.57 g/cm3,p=-36.91。以及密度递增时的参数分别为:0% → 10%时,A=1.17 g/cm3,p=4.22;0% → 30%时,A=1.17 g/cm3,p=17.96;0% → 50%时,A=1.17 g/cm3,p=36.91。其次,采用式(13)求解双层材料的等效弛豫模量g。由此,计算等效的梯度密度黏弹性介质中波的传播,结果如图8 所示,图中只列出了两种密度差别较大的情况,即50% → 0%(递减)和0% → 50%(递增)。可以看出:两种计算方法在试件两侧得到的结果基本一致;在试件夹层中间的位置,两种计算方法得到的结果差别不是很大,但有一些差异,随密度梯度增大,这种差异也越大。这体现了叠合试件中各种微结构对应力波形产生了影响。

图 8 等效梯度密度材料和双层叠合试件中的应力波形的对比Fig. 8 Comparison of stress-time curves in the equivalent gradient-density materials with those in two-layer superimposed specimens
4 结 论
推导了多层梯度密度黏弹性材料中波传播分析的理论解,结合SHPB 动态实验技术,分析了梯度钛-硼化钛材料与碳纤维增强树脂材料中波的传播过程,主要结论如下。
(1)当密度和材料的弹性常数满足一定的形式时,可得到梯度密度黏弹性材料中波传播特性的一个近似解。原则上,拟合相关材料系数,此解能够得到广泛应用。将此解应用于M层梯度密度黏弹性材料,结合层间的应力与位移连续条件和两侧的边界条件,可以得到多层介质中波传播的理论解。
(2)将此理论解应用于单层和双层梯度钛-硼化钛材料,发现:单层梯度钛-硼化钛材料中存在内界面,使得其表现出较弱的黏性,但这种黏性对SHPB 三波法分析影响不大;而双层材料的叠合产生了新的宏观界面,使其整体表现出更强的黏弹性特征,叠合试件的黏性使SHPB 三波法分析结果与材料的性能之间存在一定的差异。
(3)将此理论解应用于双层碳纤维增强树脂材料,发现:随传播距离的增加,碳纤维增强树脂材料中的应力幅值减小较大,表现出更强的黏弹性特征,此过程包括材料本身的黏性和微结构组成导致的黏性等两种机制。叠合试件的黏性使SHPB 三波法分析结果与材料的性能之间存在较大的差异。
基于此分析方法,为分析材料内部界面的实际情况,可进一步建立界面斜入射的情况。由于试样制备比较困难,本文的相关结论尚需更多验证和提高。
