双相高强钢FeNiAlC 的动态剪切行为及微结构机理*
2021-01-26袁福平武晓雷
马 彦,袁福平,武晓雷
(1. 中国科学院力学研究所非线性国家重点实验室,北京 100190;2. 中国科学院大学工程科学学院,北京 100049)
高应变速率载荷下,金属材料往往因局部化形变而失效破坏[1]。在军事工业领域,子弹的穿甲侵彻与材料的局域化绝热剪切损伤紧密相关。对实心穿甲弹,弹头的绝热剪切有利于在侵彻过程中自锐化而增大穿刺深度[2]。在航空航天领域,飞行器的安全威胁主要来自空间碎片的高速撞击,材料的绝热剪切直接导致飞行器构件的灾难性破坏。所以,金属材料的动态剪切行为是材料在特殊使用环境下必须考虑的关键问题[1-3]。
高应变速率载荷诱发材料的局部化形变,有两个基本特征:加载速度快变形过程接近绝热状态;变形区域小易形成剪切带。由于绝热剪切带(adiabatic shear band, ASB)的形成和扩展在约1 0-5s 内完成且宽度一般在102μm 内,目前仍缺乏有效的实验技术实现原位直接观测[2]。现阶段,主要手段是通过表征材料变形失效后的微观结构来分析和推演ASB 形成和扩展过程。Meyers 等[4]在低层错能304L 不锈钢动态剪切实验中,发现ASB 内形成晶粒尺寸100~200 nm 的等轴晶,通过形变织构分析,得出这些等轴晶是通过变形过程中初始晶粒的旋转、滑移和孪生机制形成的。Yang 等[5]则通过应变冻结实验,系统地研究1Cr18Ni9Ti 奥氏体型不锈钢形成ASB 过程中微结构的演化,证实ASB 内晶粒的动态旋转再结晶机制。Li 等[6]在高锰钢的子弹侵彻试验中,发现ASB 内产生明显的纳米晶区域和非晶区域,表明在ASB内由于极高的温升产生了金属熔化和快速冷却。Wei 等[7-8]则分别研究了粗晶(coarse grained, CG)、超细晶(ultrafine grained, UFG)、纳米晶(nanocrystalline, NC)结构铁在高应变率下的压缩变形,结果表明,减小晶粒尺寸会导致材料形成ASB 的概率提高,同时定量分析了应变硬化率和率敏感性对形成ASB 的影响。
目前,关于金属材料ASB 失效的基本准则是由Zener 等[9]提出的材料应变硬化与热软化相互竞争的机制,即当材料丧失应变硬化能力时发生ASB 失效。Batra 等[10]提出ASB 形成判据(最大应力准则:ASB 在流变应力达到最大值时形成并快速扩展,导致流变应力快速跌落至峰值的80%),但该准则往往仅适用于均质材料。在梯度材料[11]和多层材料[12]中,ASB 形成于材料中硬化能力较弱的区域,但由于材料的非均匀性,当局部形成ASB 后材料整体依然具有硬化能力,当ASB 贯穿整个样品时材料才会丧失承载能力。在这些异构材料[11-12]中,局部微区的力学属性差异能够延缓ASB 的形成和传播,从而延缓材料失效的发生。由此可见,材料的微观结构对形成ASB 失效非常重要。本文中,以FeNiAlC 双相钢为例,讨论不同微结构材料的剪切变形行为,进一步理解微结构对材料形成ASB 的影响以及温升和热软化对材料发生局部化变形的影响。
1 实 验
FeNiAlC 合金由纯度为99.99%的铁、镍、铝金属单质进行熔炼而成。首先,在真空电弧炉中经过5 次反复熔炼形成 ∅ 20 mm 的铸锭,测得铸锭中铁以外化学成分的质量分数为w(Ni)=24.86%,w(Al)=5.8%,w(C)=0.38%,记为Fe-24.86Ni-5.8Al-0.38C。接着,将铸锭加热至1 100 ℃后热锻成10 mm×10 mm×50 mm的钢板,在950 ℃下进行热轧,终轧厚度为6 mm,冷却至室温。然后,将热轧板在真空马弗炉中进行均匀化固熔,固熔温度为1 150 ℃,固熔24 h 后进行快速淬火处理。最后,将固熔后的金属板进行大应变冷轧处理,压下量(截面积减少量)分别为39%、53%(记为CR39、CR53),未进行冷轧处理的材料为粗晶态(记为CG)。
动态冲击样品采用强迫剪切构形试样(帽形试样),强迫剪切区宽度为200 μm,剪切方向垂直于板材轧制方向,帽形试样的厚度即为冷轧后板材的厚度,如图1 所示。实验时,将试样紧密放置于用马氏体时效钢制成的限位环中,限位环在冲击过程中变形量极小,保证样品主要受剪应力的作用。由有限元模拟结果[13],剪切区的高度(2 mm)远大于剪切区的宽度(0.2 mm),压应力相对剪应力是小量,因此帽形样品的变形过程可以近似等效为纯剪切变形。在 ∅ 13 mm 分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)装置上进行冲击实验,子弹速度约20 m/s,加载应变率范围为10 000~30 000 s-1,每个状态的样品重复5 次实验,重复性相对较好,实验误差小。通过杆上的应变片和动态应变仪测量,得到入射杆和透射杆中的反射波应变εR和透射波应变εT,进行空载标定应变片敏感系数。利用两波法和一维弹性理论,计算样品在一维应力加载下的剪切应力τs、剪切应变γs、应变率 γ˙s与和位移us:

式中:E、A和c0分别为霍普金森杆的杨氏模量(210 GPa)、横截面积(132.7 mm2)和纵波波速(5 050 m/s),As和ts分别为帽形样品的剪切区面积和宽度[14]。
实验前后样品的微观结构采用Zeiss Gemini 300 扫描电镜(scanning electron microscope, SEM)和JEOL 2100F 透射电镜(transmission electron microscope, TEM)进行表征。使用电子背散射衍射(electron backscatter diffraction, EBSD)技术获取材料的晶体学取向及位错密度等,选用Oxford Symmetry 探头进行扫描,扫描步长为50~1 000 nm,使用CHANNEL 5 软件进行数据后处理。观测前的样品准备,详见文献[15]。
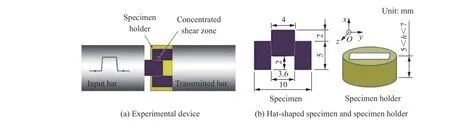
图 1 动态剪切实验装置和样品Fig. 1 Dynamic shear experimental device and its sample
2 结 果
2.1 初始微结构
冲击实验前,对CG、CR53 样品进行微结构表征。图2 为CG 样品晶粒的反极图(inverse pole figure,IPF)和相图(phase figure, PF)。固熔后样品由奥氏体相(austenite, γ)和马氏体相(martensite, α)构成,奥氏体平均晶粒尺寸较大,约为11.5 μm,马氏体相析出在奥氏体晶界处,平均晶粒尺寸约为3.55 μm,马氏体相约占15%,属于一种双相合金。由图2(a) 可见,固熔后晶粒取向随机分布,无明显织构。图3 为CR53 样品的IPF 和PF。轧制过程中发生少量马氏体相变,马氏体相比例略有增加,约占18%。奥氏体晶粒被拉长,统计晶粒的长轴和短轴比约为2.1,据晶粒被拉长计算等效应变约为0.49[16],而冷轧53%换算成等效应变约为0.50。这说明冷轧过程中,变形主要发生在奥氏体相中,马氏体相几乎不承担变形。由图3(a)可见,与粗晶态相比,冷轧后出现明显的〈111〉丝织构[17]。为了研究样品冷轧前后的位错形貌和位错密度,对CG、CR53 样品进行TEM 观察。图4(a)为CG 样品奥氏体相的形貌和[011]晶向衍射谱。固熔后样品内部有少量的平形位错,长度较短,位错密度极低。图4(b)为CR53 样品的晶粒衍衬像、α 相[001]晶向的衍射谱和γ 相[011]晶向的孪晶衍射谱,样品内部位错密度明显增大,位错大多缠结在晶界和相界附近,奥氏体晶粒内部产生少量变形孪晶。CG 和CR53 样品中晶粒形貌、尺寸和位错密度的差异,影响两种微结构样品的动态剪切行为,这将在以下作详细介绍。

图 2 实验前CG 样品的微观结构Fig. 2 Microstructures of CG sample before experiment

图 3 实验前CR53 样品的微观结构Fig. 3 Microstructures of CR53 sample before experiment

图 4 实验前CG 和CR53 样品的TEMFig. 4 TEM observations of CG and CR53 sample before experiment
2.2 动态剪切性能
用动态剪切实验所得的数据,通过式(1)获得的剪切应力与变形位移、剪切应变的关系曲线如图5所示。圆点为名义动态剪切屈服强度,CG 样品约为480 MPa,CR39、CR53 样品分别为910、1 250 MPa,冷轧量越大,样品的剪切屈服强度越高。方点为样品的最大剪切应力,根据最大剪应力准则[10],此时样品剪切区内部形成ASB,此后剪切应力快速下降,样品发生失稳破坏。在形成剪切带前,变形主要集中在宽200 μm 的剪切区内,一般认为这个过程中剪切区内的变形是均匀的[14]。图5(b)中,曲线所包围的面积可以近似为材料的动态剪切韧性。

图 5 不同微结构的动态剪切性能Fig. 5 Dynamic shear properties of various microstructures
与其他合金一样,利用帽形试样获得FeNiAlC 合金的动态剪切性能,并进行比较。图6 为FeNiAlC合金和其他常用合金(301、316 不锈钢等)的均匀剪切应变和剪切韧性与动态剪切强度的关系[13-14,18-24]。在同等动态剪切强度情况下,FeNiAlC 合金剪切韧性优于其他合金,拥有较优异的动态剪切性能。
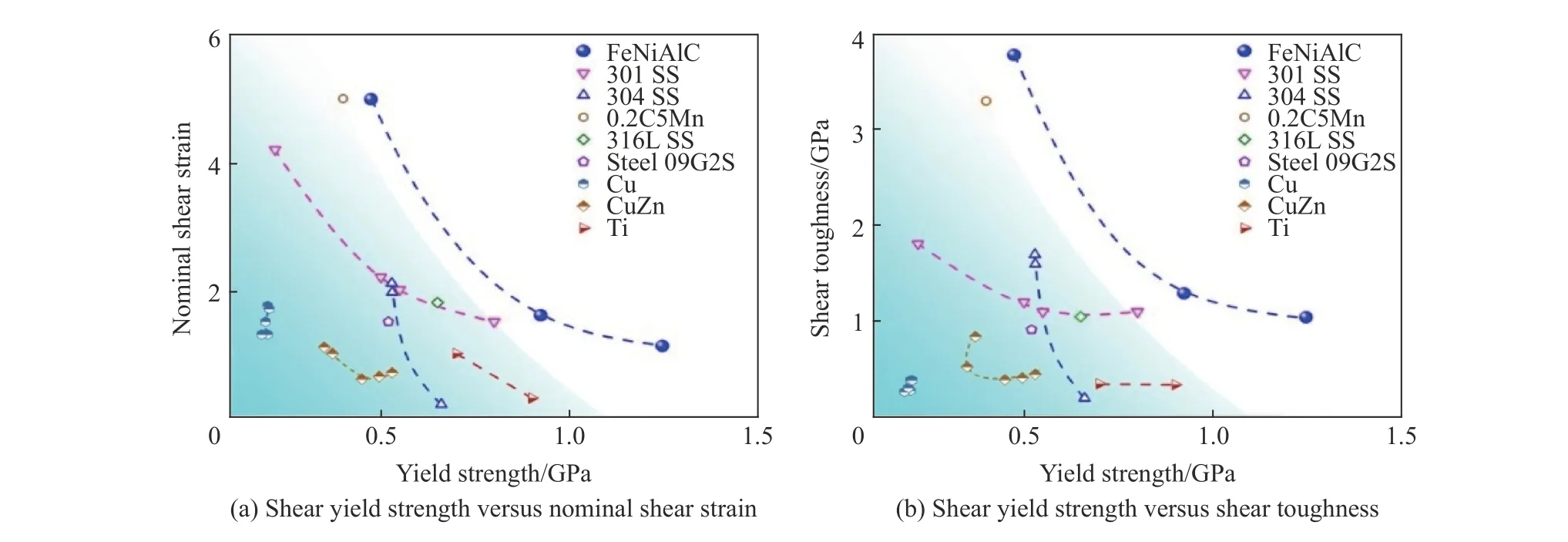
图 6 不同金属的动态剪切性能Fig. 6 Dynamic shear properties of various metals
2.3 均匀剪切变形区的孪生与位错
为了研究变形过程中微结构的变化,采用SEM 中的EBSD 技术对变形后的样品进行表征。由图7(a)~(b)可见,CG 样品中剪切区的中心有一条识别率较低的窄带(两条虚线之间)是剪切失稳后形成的ASB。ASB 两侧约100 μm 区域是主要的剪切变形区,剪切变形区内产生大量小角晶界,在奥氏体和马氏体的相界附近有大量的小晶粒产生。在等轴的奥氏体晶粒内形成大量的变形孪晶(deformation twin,DT),宽度为2~3 μm。由图7(b)可见,马氏体相所占比例约14%,与剪切变形前相比几乎没有变化,说明变形过程中没有发生马氏体相变。在图7(c)中,红线为该点与相邻点之间的取向差,蓝线为该点与初始点的取向差。每跨过一个(孪晶)界面时,取向角改变60°,这是典型的FCC 晶体Σ3 孪晶取向关系[25]。CG 样品剪切变形后孪晶密度较高,发生孪生变形的区域占总体积的60%以上,说明在此应力状态下,奥氏体晶粒大部分发生孪生变形。
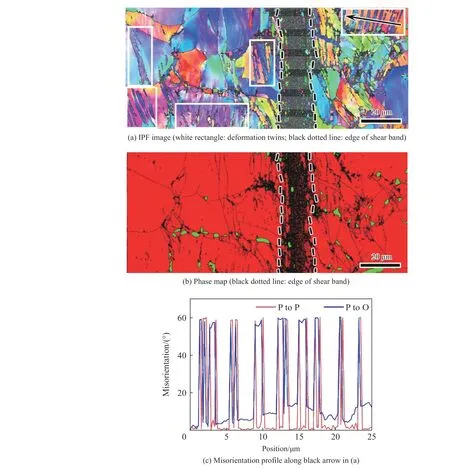
图 7 实验后CG 样品的微观结构Fig. 7 Microstructures of CG sample after experiment
由图8(a)~(b)可见,CR53 样品中靠近ASB 区域产生大量的小晶粒,与变形前相比晶粒明显细化,远离ASB 区域产生少量的孪晶。由图8(b)可见,α 相所占比例约18%,与变形前相近,说明冷轧态样品也几乎没有发生马氏体相变。由图8(c)可见,当跨过孪晶界面时,CR53 样品界面两侧取向角相差60°,同CG 样品结果类似。
KAM (kernel average misorientation)即mka,为晶粒内一点与周围相邻点的取向差的平均值,是一个与几何必需位错(geometrically necessary dislocation, GND)密度正相关的物理量[26]。图9~10 分别为CG 和CR53 样品剪切变形前后局部晶粒的KAM 及分布。分布图中,统计分布时取向差步长为0.25°。对比CG 样品剪切变形前后局部晶粒的KAM,可以得到两个有价值的结论。(1)变形前,由于经过高温长时间的固熔处理,晶粒内部取向差极小,说明此时晶粒内部位错密度极低,仅在晶界周围小于1 μm 内存在明显的取向差分布(0.5°~1.1°)。这可能是因固熔后进行快速淬火处理,在界面处会产生残余应变,引起GND 密度升高。(2)与变形前相比,剪切变形后奥氏体晶粒承担主要变形,因此在奥氏体晶粒内部出现了高密度的GND,KAM 在0.8°~2.0°,尤其在孪晶界周围,KAM 约为2°。说明变形产生大量的位错钉扎在孪晶界附近,位错与孪晶的相互作用为CG 样品在剪切变形过程中提供了较大的应变硬化能力。对比CG 态样品变形前后γ 相KAM 分布可见,由于样品中α 相含量较少,硬度较大[15],几乎不参与变形,变形前后KAM 几乎没有变化,所以这里只进行γ 相KAM 的比较。变形前KAM 平均值约为0.96°,变形后为1.26°,根据KAM 与GND 密度的关系[26],可以估计变形后GND 增加约30%。这也说明,CG 样品均匀剪应变之所以能达到5,晶粒内部有充足的可动位错参与变形。
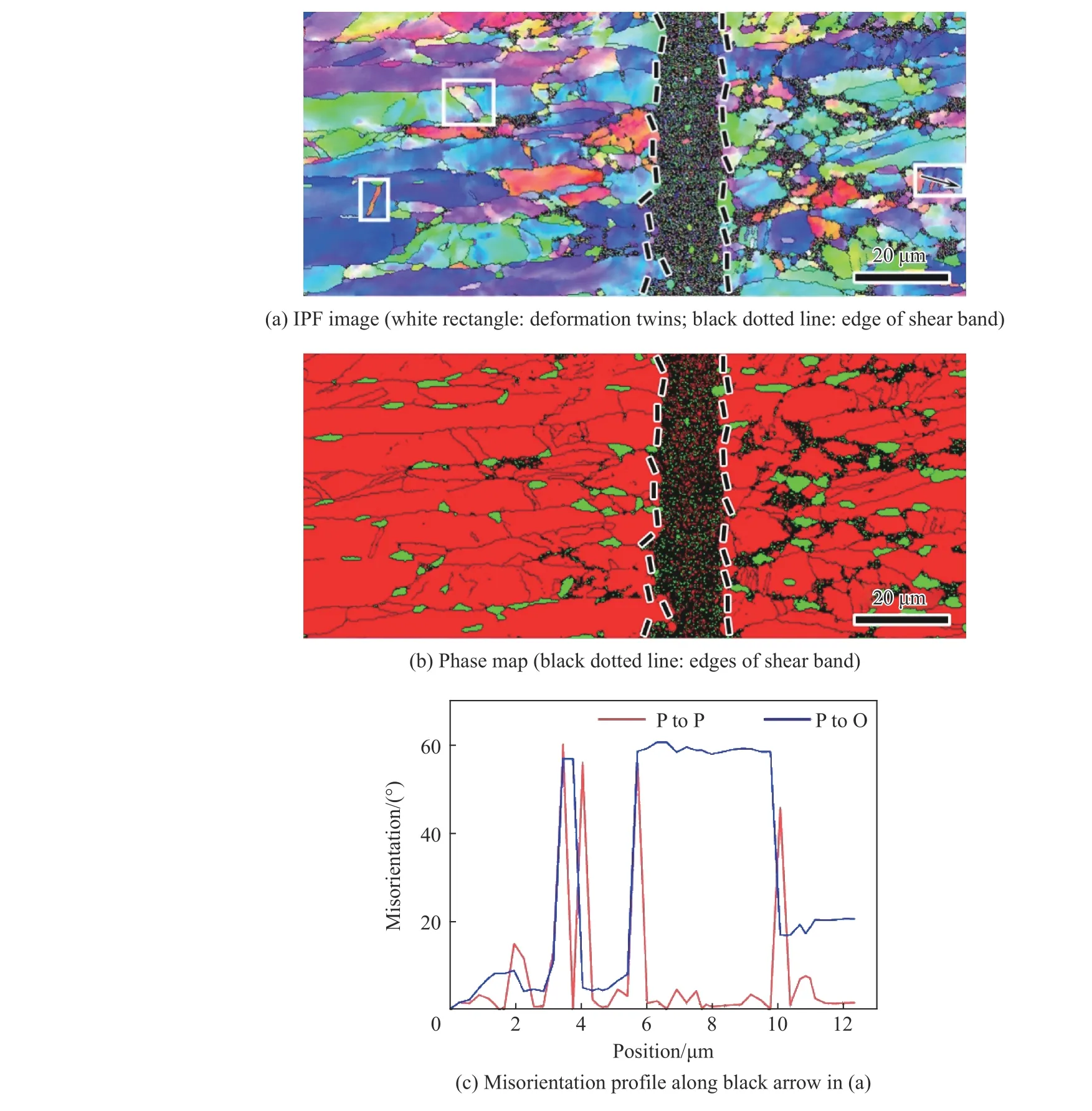
图 8 实验后CR53 样品的微观结构Fig. 8 Microstructures of CR53 sample after experiment
对比CR53 样品剪切变形前后局部晶粒的KAM 可见,由于经过大应变冷轧过程(等效应变约0.50),样品表现出很高的KAM,尤其是在晶界附近KAM 为1.8°~3.0°,远高于固熔后的CG 样品。不同于CG 样品,CR53 样品变形后晶粒内部的KAM 明显小于变形前的KAM。同样,对比CR53 样品变形前后γ 相KAM 分布可见,变形前分布范围为0.8°~3.1°,变形后减小为0.8°~2.3°,变形前平均值为1.73°,变形后减小至1.33°,根据KAM 与GND 密度的线性关系,GND 密度减小约23%。通常,变形会使位错密度增大,但由于CR53 样品变形前的位错密度已经很高,且动态实验应变率高,变形时间短,剪切区内发生绝热剪切,有较大的温升,会使局部晶粒发生部分回复。同时,该样品均匀剪切应变较小,约为1,所以剪切变形后,回复的作用大于变形的效果,KAM 不增反降,GND 密度降低,致使CR 样品应变硬化能力降低,过早的发生塑性失稳(形成ASB)。
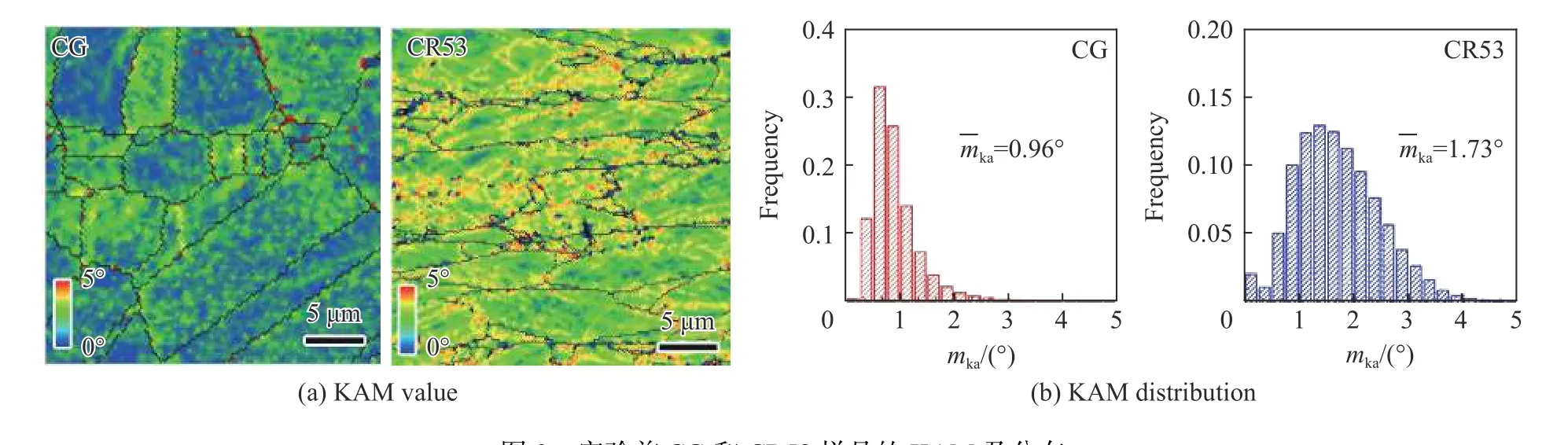
图 9 实验前CG 和CR53 样品的KAM 及分布Fig. 9 KAM values and distributions of CG and CR53 sample before experiment
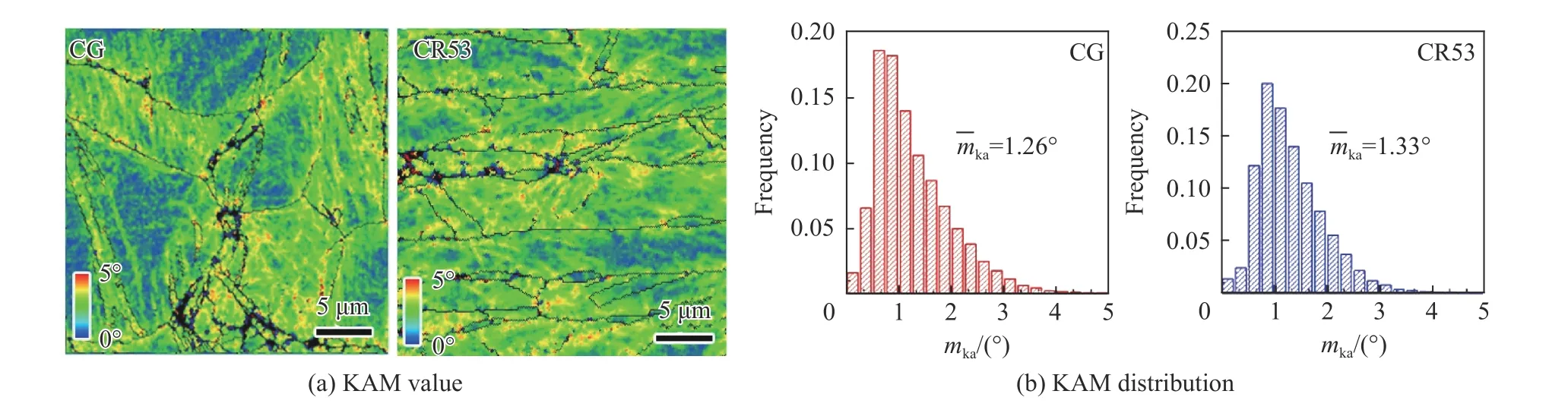
图 10 实验后CG 和CR53 样品的KAM 及分布Fig. 10 KAM values and distributions of CG and CR53 sample after experiment
2.4 绝热温升
在动态加载过程中,由于加载速度极高,变形时间在100 μs 内,热传导来不及进行,所以整个剪切过程可近似成绝热过程[1-3]。同时,认为在均匀剪切阶段,剪切区内的应变是均匀的。计算剪切过程中剪切区温升的塑性功转化温升公式为[14]:
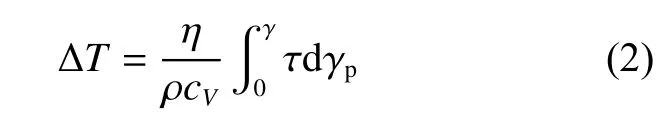
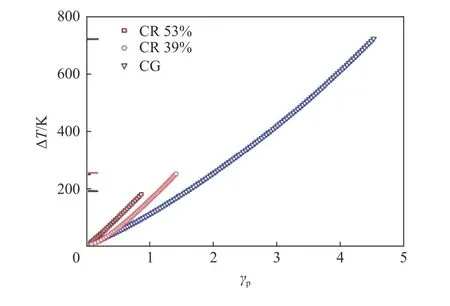
图 11 最大应力点前剪切区塑性功引起的温度升高Fig. 11 Temperature rise due to plastic dissipation work in shear zone before maximum stress point
式中:η 为总的非弹性功转化为热量的系数(Taylor-Quinney 系数),本文中取0.8;ρ 和cV为材料的密度和比热容,τ 和γp为剪切应力和剪切塑性应变。对FeNiAlC 合金,测得ρ 为9.8 g/cm3,cV取540 J/(kg·K)[27]。图11 为用实验所测的剪切应力和应变、据式(2)计算的温升曲线。CR 样品的温升斜率明显高于CG 样品,这是因为CR 样品由于冷轧过程中引入大量的可动位错及位错胞等亚结构,在塑性变形初期剪切流变应力大,导致温升的斜率高于CG 样品。当剪应变达到0.5 时,CR 样品的温升约为100 K,CG 样品只有50 K,而当剪应变达到最大均匀剪应变时,CR53 样品最终温升达到190 K,而CG 样品最终温升高达720 K。这表明,绝热温升可能不是ASB 形成的主导或者唯一因素[27-28]。
2.5 绝热剪切带
一般认为,ASB 是材料受到冲击载荷作用时的一种失效模式[1-2]。当材料受到高速率剪切力时,通常认为材料的失效是塑性应变硬化和绝热温升所致的热软化相互竞争的结果[9]。变形初期,温升较小,材料的应变硬化占据主导,发生均匀变形,剪切应力不断提高。当剪切区温升达到一定值时,材料的应变硬化不足以抵抗温升带来的热软化,材料发生局部化变形,剪切应力骤然下降,形成ASB。图7~8 中未能解析的带状部分就是变形形成的ASB。因为带内发生了比带外高1~2 个数量级的变形,所以当前的扫描步长不足以解析其微结构。对于ASB 内的微结构采用40 nm 的步长重新扫描,如图12 所示。CG 样品ASB 内晶粒不同于剪切区的晶粒发生孪生变形或局部晶粒细化,而是形成了大小几乎相等的等轴晶。晶粒尺寸集中在200~500 nm,远远小于初始的晶粒尺寸(13 μm)。由此可得,在ASB 形成时带内组织发生了动态再结晶(dynamic recrystallization, DRX),与大多数金属材料类似[14],在大应变和高温的作用下,ASB 内形成取向随机、大小相等的再结晶晶粒。同CG 样品相似,CR53 样品同样发生了DRX。CG 和CR53 两种样品ASB 内虽然应变极大,但均不发生相变,只是在原有马氏体相的基础上发生晶粒细化,没有形成新的马氏体相。
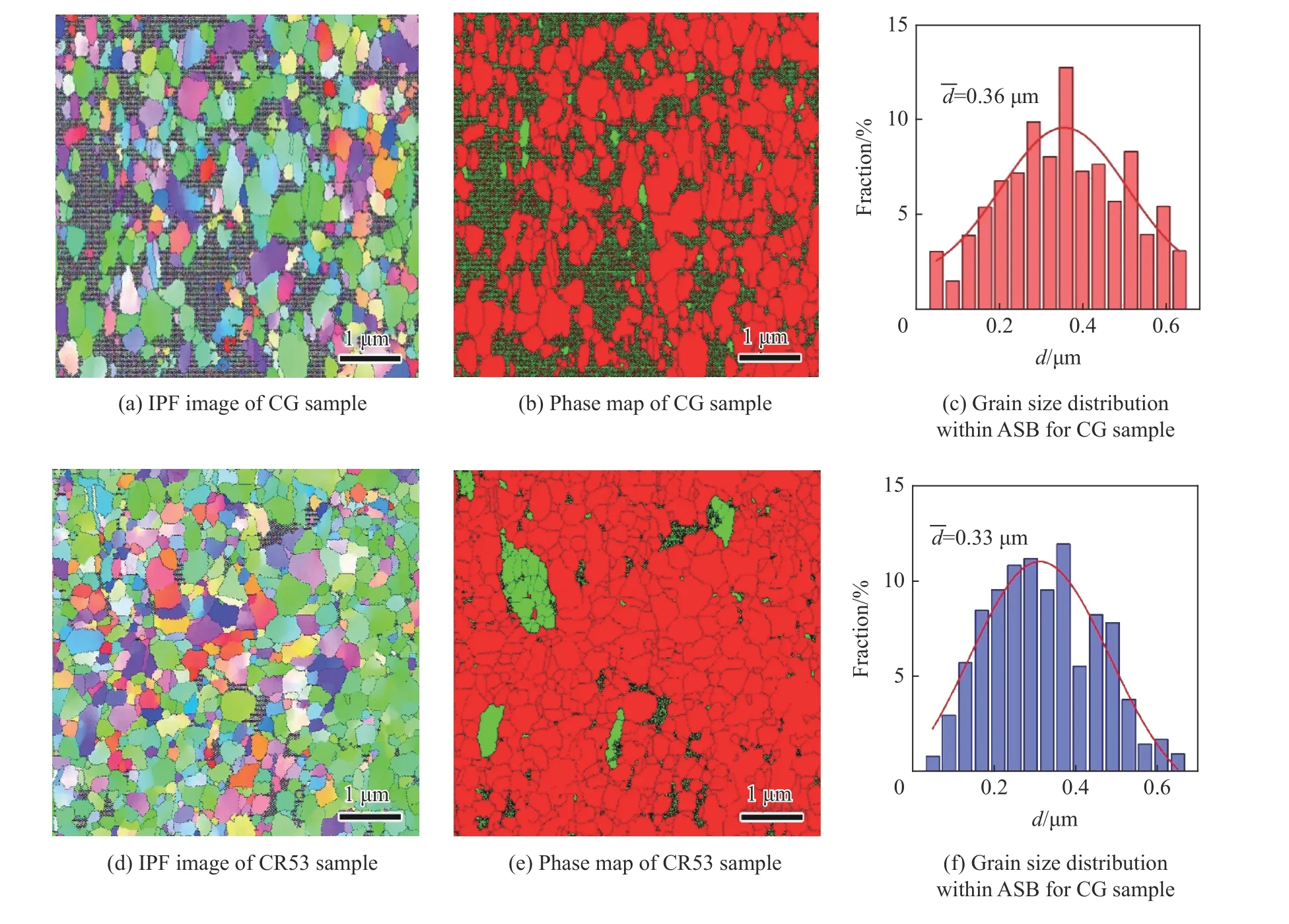
图 12 绝热剪切带内微观结构Fig. 12 Microstructures within ASBs
根据热塑模型理论[1],材料发生ASB 失效时,剪切带的宽度可以通过材料所受最大剪应力和应变率等进行估算。Dodd 等[1]提出剪切带宽度的计算公式:

式中:τ 和 γ˙ 分别为形成剪切带时的剪应力和剪应变率,T为试样温度,λ 为热传导系数(不锈钢约为15 W/(m·K)[28]。基于前面的实验和计算结果,CG 样品剪切带的理论宽度为29.7 μm(T=1 018 K,τ=1 100 MPa,γ˙ =63 000 s-1),CR53 样品的为14.6 μm (T=468 K,τ=1 340 MPa, γ˙ =98 000 s-1)。图7~8 中的剪切带宽度并不是均匀的,受到局部微结构和受力状态的影响较大。通过划线法统计剪切带的宽度,结果如图13 所示。CG 样品剪切带的宽度范围为12~19 μm,平均值为15.8 μm,而CR53 样品剪切带宽度范围为9~15 μm,平均值为12.3 μm。对比来看,CR53 样品的理论计算ASB 宽度更接近于实验所测真实宽度,而CG 样品的实际剪切带宽度范围小于理论计算值。这可能是根据塑性功计算样品温度带来的影响。热塑模型的基础是理想的绝热条件,而实际实验过程中:CR53 样品从加载到ASB 失效过程较短,更接近绝热条件;CG 样品具有较好的应变硬化能力,因此从加载至产生ASB 失效经历时间更长,考虑到热耗散因素,实际的剪切带宽度小于理论值。

图 13 绝热剪切带宽度分布Fig. 13 ASBs width distributions
3 讨 论
在FeNiAlC 合金准静态拉伸变形的研究[15]中,CG 样品的主要变形方式为位错滑移和少量孪生变形,硬化能力较弱。而在本文中,由于应变率提高约108倍,面心立方结构一般具有正的率敏感系数,动态条件下会显著提升流变应力水平,极大地促进孪晶的形成[29-30],变形方式以孪晶与位错交互作用为主导,因此剪切韧性得到充分提升。在准静态拉伸下,CR 样品变形方式以位错滑移和马氏体相变为主,相变诱导塑性(transformation induced plasticity,TRIP)效应显著,所以保持了较高的均匀塑性。但在动态剪切加载下,由于应变速率的提高,局部温升导致材料层错能升高,马氏体相变被抑制[31],因此应变硬化能力不足导致过早地发生局部失稳。同时,CR 样品冷轧后,由于存在明显的织构不易于发生孪生变形[17],所以在动态剪切时,屈服后硬化能力不足,较早地发生失稳。
ASB 的萌生、绝热温升和应力骤降三者的因果关系,一直是材料绝热剪切变形研究的热点问题之一[3,27]。在热塑模型理论中,认为绝热温升是形成ASB 失效的主要原因,最大应力准则也是建立在温升导致的ASB 形成后产生应力的骤然下降上。但是,由于动态冲击的变形特点(高应变率和极短时间),ASB 范围极窄,形成速度极快与载荷下降时间相差无几,所以一直没有明确的实验证据证实三者的先后关系。Guo 等[27-28]试图用实验证实材料剪切带失效与温升的关系,结果表明:在Ti 合金中ASB 的萌生先于塑性变形产生明显温升,而材料的最大应力也出现在ASB 萌生前。该结果与传统的热塑模型所给的预测结论相悖。本文中关于绝热剪切带热塑模型分析计算的结果与实验结果对比显示,当剪切变形时间较长时(材料的硬化能力较强),变形过程与热塑模型的理论前提(理想绝热条件)有所差异,材料的热耗散和微观结构变形不均匀等原因会影响ASB 的形成和扩展,使热塑模型的结论与真实实验结果相差较大。同时,本文中也证实了绝热温升不是双相钢材料形成ASB 的主导因素或唯一因素,还应考虑共同影响材料ASB 失效过程的局部化应变和材料微观结构演化等。
4 结 论
对FeNiAlC 合金进行帽形冲击实验,研究其动态剪切变形行为和微结构机理。实验主要对均匀化处理的粗晶结构样品和冷轧后的层状结构样品进行强迫剪切,研究不同结构样品均匀变形过程和发生ASB失效前后的微观结构变化,利用热塑模型对ASB 宽度和塑性功的热转化温升进行分析,主要结论如下。
(1)FeNiAlC 双相钢拥有较优异的动态剪切性能,剪切强度为400~1 300 MPa,剪切应变为1.5~5.1。同等剪切强度的剪切韧性均高于传统的TWIP 钢、304、316 不锈钢等合金材料。
(2)孪生与位错主导剪切变形过程中,CG 样品在变形过程中发生大量的孪生变形,位错密度显著提高,位错与孪晶界的交互作用使材料获得良好的硬化能力,提高了剪切韧性。CR 样品因在剪切变形前冷轧引入大量的位错,变形初期位错密度极高,屈服强度达1.3 GPa,同时因冷轧织构的存在抑制孪生变形;变形过程中,绝热温升使位错发生部分回复,材料的应变硬化能力不及CG 样品,屈服后在较小的均匀应变下形成绝热剪切带,发生失稳。动态剪切下,材料的马氏体相变被抑制。
(3)绝热剪切带内发生动态再结晶,形成晶粒取向随机的超细晶晶粒,同时因剪切带内极高的温度,带内不发生马氏体相变。
(4)热塑模型在应变较小的情况能够与实验结果高度吻合;绝热温升不是ASB 形成的主导因素或唯一因素,ASB 的形成可能由局部化变形、材料的微观结构演化等影响。
