基于PCA-FUZZY的城镇化发展水平综合评价
2021-01-25赵文英于良娟谢威祖培福
赵文英 于良娟 谢威 祖培福


摘 要:构建测量城镇化水平的综合指标体系,评价我国城镇化水平.采用“主成分-模糊综合评价法(PCA-FUZZY)”对我国2004-2017年的城镇化水平进行综合评价.结果表明:我国城镇化水平呈现稳步增长;国家需要在提高就业率和增加城市绿化面积问题上加大投入力度.主成分-模糊综合评价法去除了指标间信息重叠的问题,将具有不明确意义的主成分进行模糊综合评价,避免了两种方法的一些缺点,其评价结果可信度更高.
关键词:城镇化;PCA-FUZZY法;指标体系;综合评价
[中图分类号]F727 [文献标志码]A
Application of Improved Fuzzy Comprehensive Evaluation Method in
Comprehensive Evaluation of Urbanization Development Level
ZHAO Wenying,YU Liangjuan,XIE Wei,ZU Peifu
(School of Mathematical Science,Mudanjiang Normal College,Mudanjiang 157011,China)
Abstract:In order to measure the level of urbanization in China,the comprehensive index system has been constructed.Principal component fuzzy comprehensive evaluation method (PCA-FUZZY) is adopted to evaluate the urbanization level of China from 2004 to 2017.The results show that the level of urbanization in China is increasing steadily;At the same time,the state also needs to increase investment in improving employment rate and increasing urban green area;In the PCA-FUZZY method,the problem of overlapping information between indicators is eliminated,and the fuzzy comprehensive evaluation of principal components with unclear meaning is carried out,which avoids some shortcomings of the two methods,and its evaluation results have higher credibility.
Key words:urbanization;PCA-FUZZY method;index system;comprehensive evaluation
我國的经济和社会发展取得了举世瞩目的重大成就,城镇化水平也随之有了显著提高.城镇化是乡村变成城镇的一个复杂过程,是衡量一个国家和地区经济社会发展的主要标志[1-5].城镇化过程是一个包含着社会众多方面指标改变的复杂过程,有必要对各项指标进行有效评价.笔者采用“主成分-模糊综合评价法”对我国2004-2017年的城镇化水平进行评价和分析,提出进一步提高我国城镇化水平的建议.
1 指标体系与评价方法的构建
1.1 指标体系的构建
城镇化过程不仅包含了城市的变化过程,也包含了农村农民的变化过程.[2]笔者结合社会学、人口学、经济学、地理学的城镇化定义,将城镇化评价指标体系定为经济城镇化、人口城镇化、居民生活城镇化、环境城镇化、科技城镇化、农村和农民城镇化六方面,每方面选取表征本类典型的正向指标作为具体评价指标.具体指标体系见表1.
1.2 评价方法的构建
城镇化水平指标存在着或多或少的联系,如果直接利用这些指标进行评价,将无法避免指标间信息的重叠问题.故采用主成分分析法将指标降维,重新组合,去除指标间的信息重叠.
单一的主成分分析方法的缺点是大多数主成分的意义不甚明确,充满模糊性,如果用此排序评价,结果必将存疑.为解决这一问题,笔者采用主成分改进的模糊综合评价方法——主成分-模糊综合评价法(简称PCA-FUZZY法)——克服指标间信息重叠问题和模糊综合评价中指标权重主观性强的问题,可满足模糊综合评价方法指标间不相关的条件,使得评价结果可信度更高.
PCA-FUZZY法的步骤:
(1)建立原始数据矩阵x=(xij)m×n={x1,x2,…,xn};
(2)将x进行标准化,标准化公式X′ij=xij-x-jsj,矩阵为X=(Xij)m×n=(X1,X2,…,Xn);
(3)利用标准化后的矩阵X计算协方差矩阵H,确定主成分Fi.其中,H=(hij)n×n,hij=
∑nk=1Xki-X-iXkj-X-j∑nk=1Xki-X-i2∑nk=1Xkj-X-j12,
(i=1,2,…,n;j=1,2,…,n);
(4)计算H的特征值λp和正交化单位特征向量up,其中u1=a11a21…ap1,u2=a12a22…ap2,…,up=a1pa2p…app,从而得到主成分指标为:Fi=a′iX,i=1,…,p.
(5)将主成分指标作为模糊综合评价的因素集U={F1,F2,…,Fp},每个Fi的权重为其方差贡献率αi,i=1,…,p,建立权重矩阵A;
(6)将每一年作为评价集V={V1,V2,…,Vs};
(7)建立因素集每个Fi的隶属度函数,计算得到模糊关系矩阵R;
(8)模糊综合评价B=A×R.
2 PCA-FUZZY法的应用
2.1 模糊综合评价指标的获取
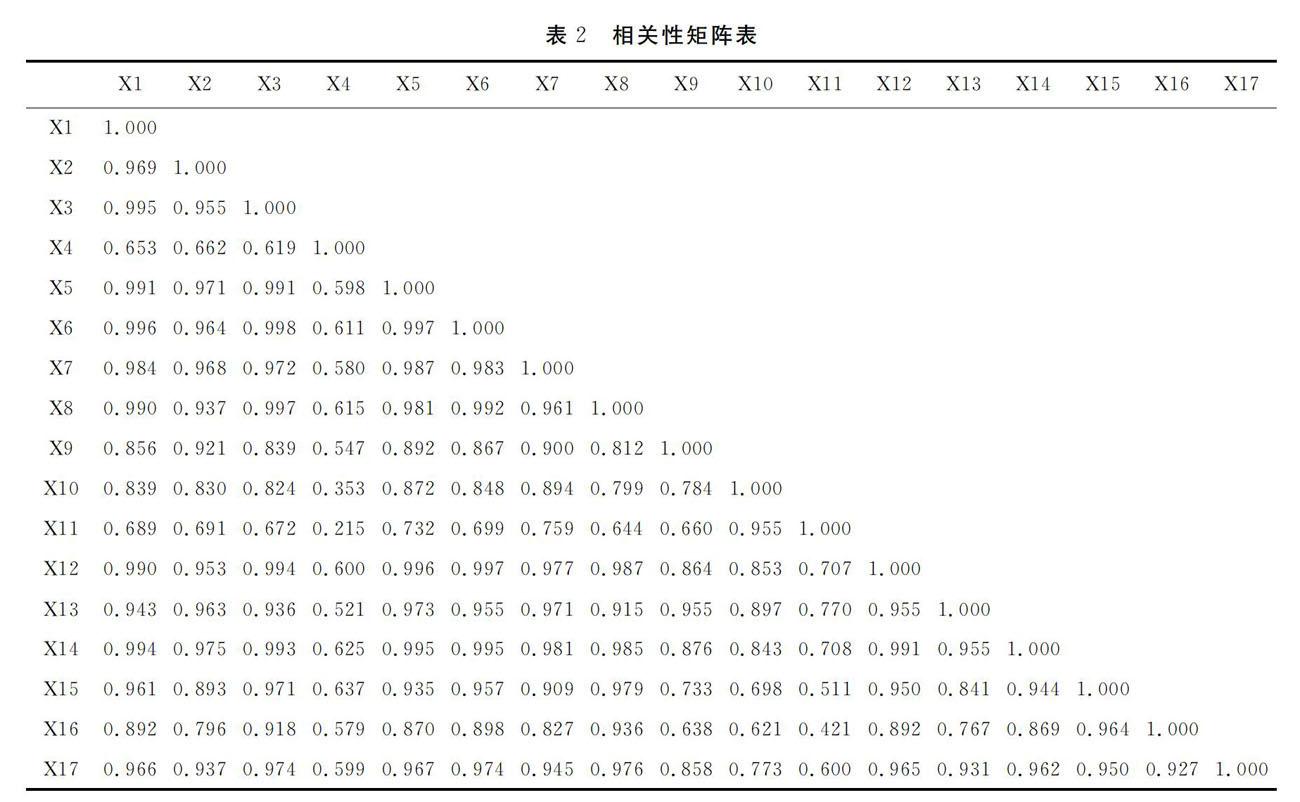
根据表1的指标查找历年数据,确定矩阵x,进行数据处理,利用统计软件进行主成分分析,得到模糊综合评价的因素集U.数据来源于中国统计局和2019年中国农村统计年鉴,截取的时间段为2004年-2017年.
相关矩阵(表2)中绝大多数数据在0.5以上,有大部分相关系数已经达到0.8以上.说明在模糊综合评价前进行主成分分析的过程是必要的.表3为特征值和累积方差贡献率.从表3中可以得到两个主成分就可以提取原信息的94%.考虑到还要进行下一步模糊综合评价,损失的信息应越少越好,因此,本文选择4个主成分作为模糊综合评价的指标,提取的信息量是原数据信息量的99%,接近于全部信息.历年的主成分得分即为模糊综合评价的评价指标.模型为:
F1=0.258 6X1+0.253 0X2+0.257 8X3+0.162 5X4+0.259 3X5+0.259 1X6+0.256 7X7+0.255 6X8+0.230 3X9+0.224 7X10+0.187 2X11+0.258 1X12+0.251 0X13+0.258 3X14+0.244 7X15+0.228 2X16+0.252 4X17.
F2=-0.052 4X1+0.002 5X2-0.067 2X3-0.473 9X4+0.025 7X5-0.025 1X6+0.079 4X7-0.102 6X8+0.128 3X9+0.430 7X10+0.595 1X11-0.010 6X12+0.159 5X13-0.014 9X14-0.243 6X15-0.310 2X16-0.110 4X17.
F3=-0.014 6X1+0.192 6X2-0.109 5X3+0.731 0X4-0.020 3X5-0.067 4X6+0.028 6X7-0.162 8X8+0.349 3X9+0.023 0X10+0.081 2X11-0.075 3X12+0.095X13-0.004 1X14-0.238 8X15-0.407 2X16-0.128 1X17.
F4=0.069 5X1-0.149 3X2+0.046 4X3+0.412 2X4-0.035 1X5+0.004 1X6-0.034 2X7+0.072 3X8-0.620 5X9+0.275 5X10+0.441 0X11+0.015 2X12-0.286 1X13-0.004 9X14+0.094 5X15+0.125 0X16-0.177 7X17.
從主成分F1的系数来看,系数较大的有很多项,很难将其归为哪一类明确的信息;从Fi,i=2,…,4的系数来看,系数绝对值较大的项符号各异,也很难进行字面意义的归类和命名.综上可以看出,主成分的意义的确是模糊的,接下来进行模糊综合评价是合理的.
2.2 模糊综合评价法的应用
第一步,将标准化的数据带入主成分得分模型,得到模糊综合评价中评价指标的因素集U={F1,F2,F3,F4},其每一个因素的权重为
A=(α1,α2,α3,α4)=0.872 170.990 93,0.068 030.990 93,0.032 250.990 93,0.018 480.990 93
第二步,要建立每个指标的隶属度函数.考虑到每个评价因子的值都是越大评价结果越好,因此,采用三角形隶属度函数,具体形式为:
r(F1)=0,Fk1≤-7Fk1+714,-7
r(F3)=0,Fk3≤-1Fk3+12.5,-1
其中,Fki表示第i个评价因子的第k个样本的值,k=1,2,…,14.将Fki的值带入到上面相应的隶属度函数中,得到模糊关系矩阵R:
第三步,根据步骤(8)得到我国2004-2017年城镇化水平的评价结果,详见表4.
3 结果分析
表4的数据显示,2004-2017年,我国的城镇化水平综合值从0.014 01到0.125 36,呈现增长趋势,大致呈线性,表明随着各行各业的全面发展,我国在经济城镇化、人口城镇化、居民生活水平、科技城镇化、农村和农民的城镇化水平上都得到了稳步提升.
从具体增长值来看,2005年增长程度为66.9%,2007增长程度为82.1%,为历年增长程度之最,其主要原因为居民人均GDP、社会消费品零售额、人均教育资金的投入增长都超过了13%;2007年城市绿地面积占城市建成区面积比增长超过了22%.自2011年开始,综合评价值相对增长基本保持在8%左右,很稳定.说明在这些年里,各行各业已经基本形成了稳定增长方式.
从具体指标看,2011-2017年,相对增长最快的是居民人均GDP和每万人拥有卫生技术人员个数,这两个指标总体拉高了城镇化水平的综合值.我国一直致力于将各行各类产业从劳动密集型向知识密集型、技术密集型转变,原有的低水平劳动力逐渐被机器和高科技所替代,需要的人员也是有技术有知识的高水平劳动力.这是导致城镇登记就业率发展较慢的重要原因之一.另外,伴随我国经济的发展,农村人口大量涌入城市,城市规模随之不断扩大,为了优先安排居住,发展工商业,为人们提供基本生活保障,城市绿化面积短期内必然会出现增长缓慢的现象.可见,国家需要在提高就业率和增加城市绿化面积问题上加大投入力度.
4 小结
本文利用主成分-模糊综合评价法对我国历年的城镇化水平进行综合评价,得出这些年我国的综合城镇化水平一直呈现稳步增长的良好趋势,但绿化面积、城镇登记就业率这两个指标的增长并不明显,说明我国要想加快城镇化水平,就必须在这两方面下功夫.主成分-模糊綜合评价法去除了指标间信息重叠的问题,将具有不明确意义的主成分进行模糊综合评价,避免了两种方法的一些缺点,其评价结果可信度更高一些,可以用来处理一些其他类似问题,是一种值得推广和借鉴的综合评价方法.参考文献
[1]刘雅静.城镇化发展水平综合评估指标体系研究[J].中共银川市委党校学报,2012,14(2):50-52.
[2]周一星.城市地理学[M].上海:商务印书馆,2003.59,64-67,134-139.
[3]何平,倪苹.中国城镇化质量研究[J].统计研究,2013,30(6):11-18.
[4]安晓亮,安瓦尔·买买提明.新疆新型城镇化水平综合评价研究[J].城市规划,2013,37(7):23-27.
[5]赵文英.基于主成分—灰色关联度的黑龙江省城镇化水平综合评价[J].数学的实践与认识,2014,44(6):43-50.
[6]赵文英,袁赫.基于改进logistic模型的中国社会消费品零售总额预测[J].牡丹江师范学院学报:自然科学版,2018(4):15-18.
[7]李淑凤,谢威.基于GM(1,1)模型的牡丹江市林产总值预测[J].牡丹江师范学院学报:自然科学版,2018(2):24-25+38.
收稿日期:2020-09-20
基金项目:黑龙江省教育教学改革一般项目(SJGY20180515);牡丹江师范学院创新创业特色项目(201910233053);牡丹江师范学院学位与研究生教育教学改革项目(MSY-YJG-2018YB014)
作者简介:赵文英(1978-),女,辽宁朝阳人.副教授,硕士,主要从事数学建模和城镇化问题研究;于良娟(1998-),女,黑龙江穆棱人.2020级在读研究生,主要从事数学建模研究;谢威(1981-),女,辽宁葫芦岛人.副教授,硕士,主要从事数学建模和区域经济预测研究;祖培福( 1981- ),男,山东临沂人.副教授,硕士,主要从事应用统计学和数学模型研究.
