截断式原模图低密度奇偶校验卷积码边扩展优化
2021-01-25洪少华马文卓
洪少华 马文卓 王 琳
①(厦门大学信息与通信工程系 厦门 361005)
②(厦门大学深圳研究院 深圳 518057)
1 引言
第6代(6G)移动通信网络是万物互联的通信网络,其数据业务传输,需要设计高效的编译码方案,以满足“超高可靠、超低时延、海量连接”的通信需求[1,2]。截断式原模图低密度奇偶校验(Low-Density Parity-Check, LDPC)卷积码是Mitchell等人[3]通过截断原模图LDPC卷积码半无限长结构的基础矩阵提出的渐近LDPC分组码,其性能好于对应的咬尾卷积码和分组码[4,5]。此外,截断式原模图LDPC卷积码可以通过滑动窗译码算法实现译码,在保证译码性能的同时具有低时延的特点[6-10]。可以说,截断式原模图LDPC卷积码结合了原模图LDPC码和卷积码的优点,具有多变的编码构造方式、优良的纠错性能以及低时延的编译码特性而深受广泛关注[11,12]。
众所周知,基于原模图构造的LDPC码,其基础矩阵B对码型性能具有重要的影响。在获得较优基础矩阵B,截断式原模图LDPC卷积码的构造需要将B分解成若干个大小相等的子矩阵,该步骤称为边扩展(edge spreading)。研究表明,截断式原模图LDPC卷积码的迭代译码门限和最小距离增长率依赖于组合子矩阵的选取,即不同的边扩展方法影响着所构造的截断式原模图LDPC卷积码的性能[13]。目前,已有多种边扩展方法[13-15],如基于基础矩阵行数和列数的最大公约数分割的公约数分解法[16],这样分解得到的子矩阵,度分布不均匀且会出现全0行;选取基础矩阵对角元素进行分割且保证分解后的子矩阵元素值不存在大于2的对角分解法,这样分解得到的子矩阵度分布相对平均;选取其中一个子矩阵稀疏,出现度为2的校验节点的低度数分解法。文献[13-15]通过对比不同边扩展方法,给出一些边扩展指导思想,如避免出现全0行或全0列,避免出现度数过低的校验节点,分解得到的子矩阵的度分布尽量均匀等;然而基于满足这些指导思想的组合子矩阵有多种,且这些指导思想并不一定适用于所有的码型。为此,本文提出一种边扩展优化方法,本方法以最小化译码门限为目标,基于给定的条件利用差分进化算法搜索最优的边扩展方式。仿真结果表明所提边扩展优化方法具有更好的性能。本文第2节简单介绍截断式原模图LDPC卷积码;第3节详细描述了所提的边扩展优化方法;第4节给出了仿真结果与分析,第5节对全文进行了总结。
2 截断式原模图LDPC卷积码


3 基于差分进化算法的边扩展优化方法
为了寻找最优的边扩展方法,最直接的方法是遍历所有的边扩展组合,选择其中译码门限最低的组合即为最优的边扩展方法。显然遍历方法非常的耗时,根本不切实际。差分进化算法[17]是一种参数优化算法,广泛应用于优化不规则LDPC码的度分布,并且可以避免错误的收敛[18-20]。为此,本文提出一种基于差分进化算法的边扩展优化方法。该方法以最小化译码门限为目标,基于给定的条件利用差分进化算法搜索最优的边扩展方式,具体表示为



4 仿真结果与分析


表1 R4JA码不同边扩展方法在L = 3的基础矩阵的译码门限(dB)

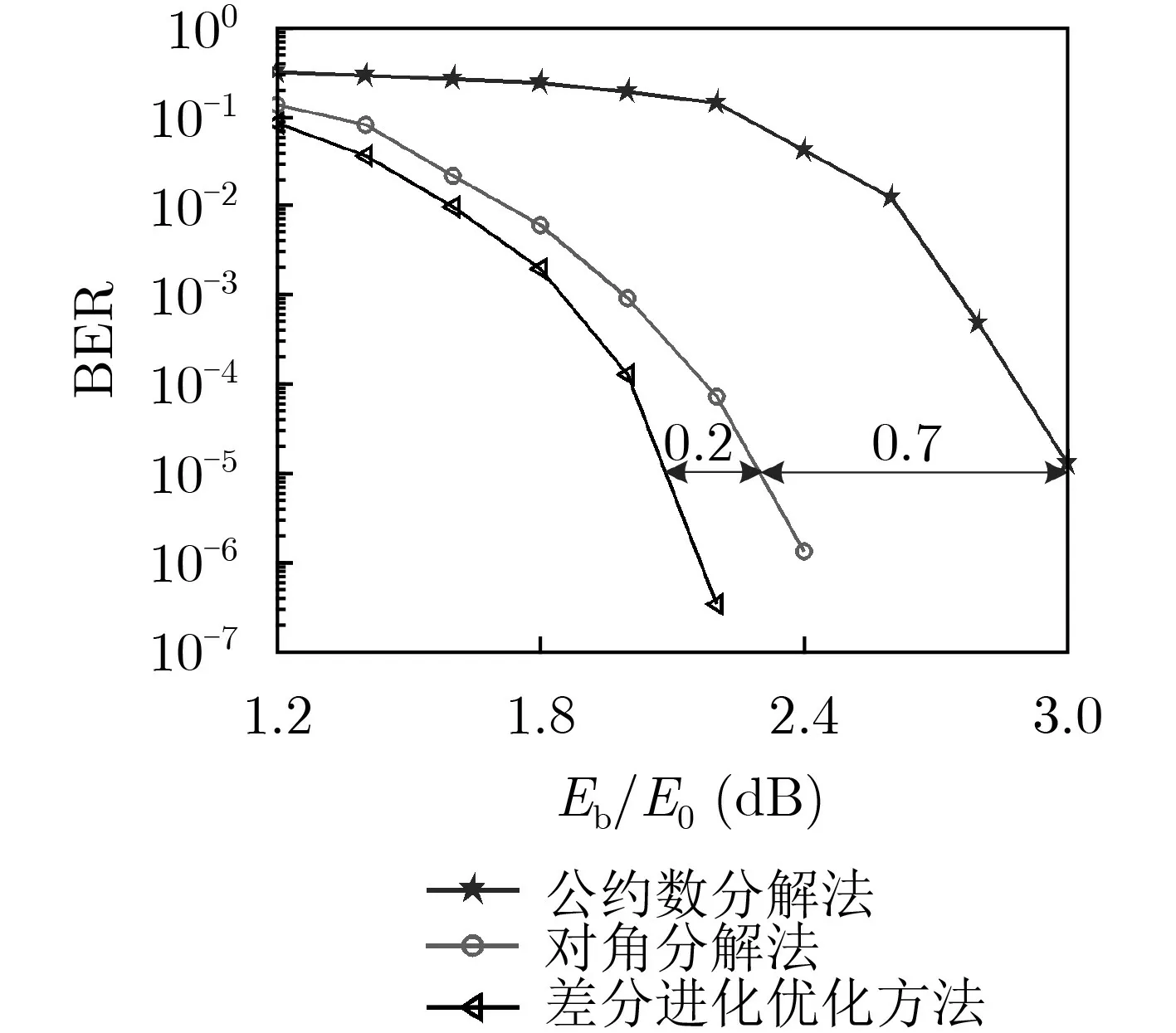
图1 R4JA码不同边扩展方法的BER性能

表2 R4JA码构造截断式原模图LDPC卷积码参数


表3 AR4JA码不同边扩展方法在L = 3的基础矩阵的译码门限(dB)
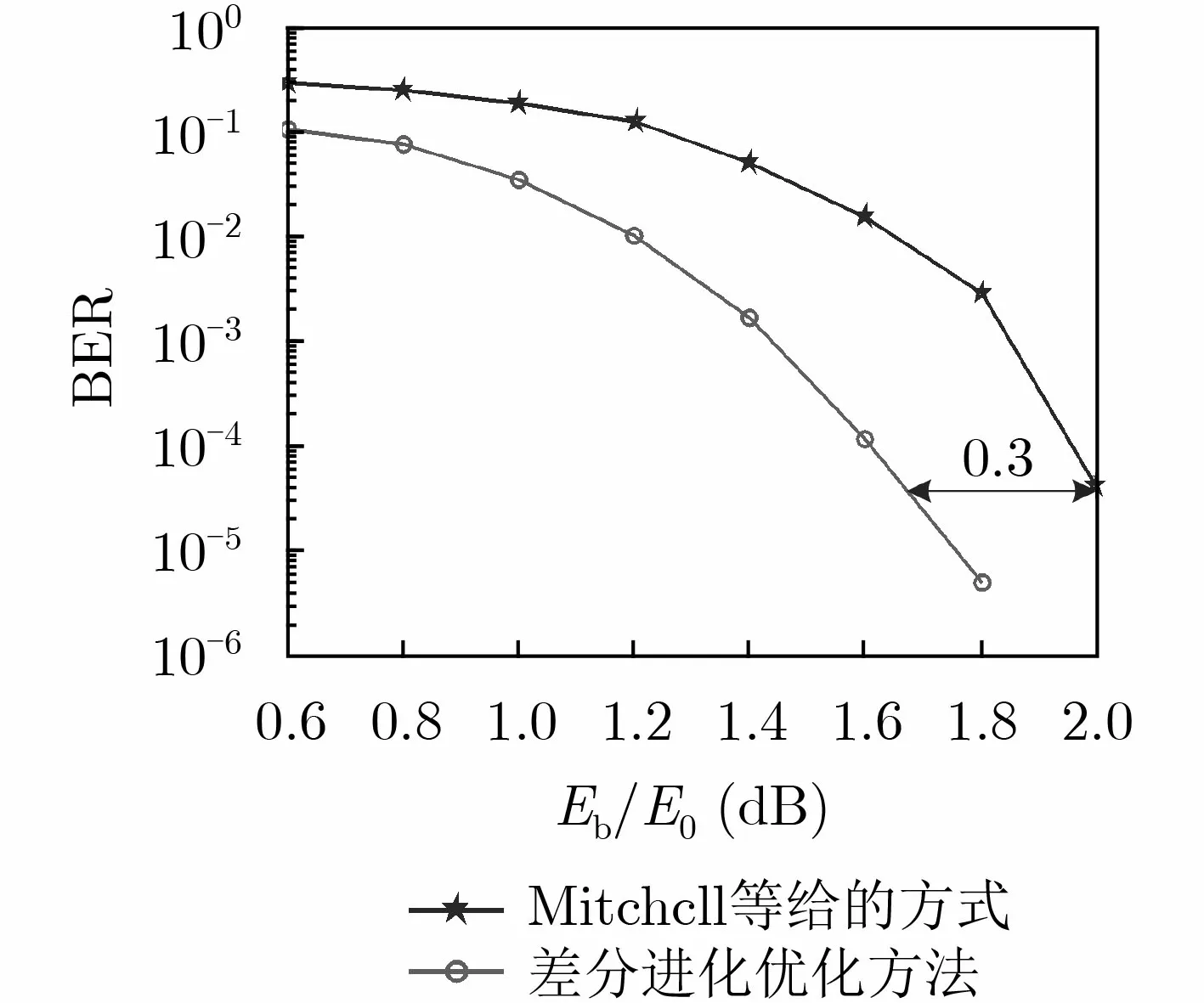
图2 AR4JA码不同边扩展方法的BER性能

表4 AR4JA码构造截断式原模图LDPC卷积码参数

表5 AR4JA码在不同截断因子L的基础矩阵的译码门限 (dB)
R4JA码与累积重复4参差累积(Accumulate-Repeat-by-4-Jagged-Accumulate, AR4JA)码是广泛应用的非删余与删余的原模图LDPC码,具有性能良好、码率可扩展等特性。本节将以这两种码型1/2码率的基础矩阵构造截断式原模图LDPC卷积码,对比不同边扩展方法的性能。两种方法的译码门限差异逐渐变小。这是因为随着截断因子 L的增大,趋向无穷大时,所构造的截断式原模图LDPC卷积码的基础矩阵即使采用的边扩展方法不同,均将趋近于非截断的半无限长结构,其译码门限均将逼近于香农限。为此,可以推断,当截断因子继续增大,两种边扩展方法的译码门限将趋向一样,逼近于香农限,与文献[13]的结论一致。
5 结论
针对截断式原模图LDPC卷积码的边扩展步骤,本文提出一种优化方法。本方法以最小化译码门限为目标,基于给定的条件利用差分进化算法搜索最优的边扩展方式。相比于现有的边扩展方法,P-EXIT理论分析与系统仿真结果均表明所提出的边扩展优化方法在给定的截断因子具有更好的性能。
