基于监测及Kriging方法的京津冀地区大气污染物暴露分布研究

2021-01-25王占山李志刚李晓倩薛凯兵王孜晔朱晓晶魏永杰

环境科学研究 2021年1期

王占山，李志刚，钱岩，李晓倩，郭辰，薛凯兵，王孜晔，朱晓晶，魏永杰

中国环境科学研究院，环境基准与风险评估国家重点实验室，北京 100012

随着我国工业化和城市化进程的加快，城市生态环境日益恶化，成为制约经济发展、危害人体健康的重要因素[1-3]. 关于大气污染物对人体暴露风险的评估成为当前环境领域研究的热点和重点[4]. 空气污染暴露风险评估依赖于连续一致的浓度空间分布，以及尽量精细化到每个个体的暴露水平估算，但受限于目前我国仪器设备、资金和人力等因素，很难实现采用每个个体佩戴暴露装置的措施，同时，空气质量监测点位的数量和密度只能观测有限空间范围内的污染物浓度，不足以支撑科学全面的污染精细化暴露评估[5]. 以往在进行人群暴露水平研究时，常用以下两种方式进行：①假设所有污染物在空间内均具有相同浓度，用某一个站点的数据代表一个城市的暴露水平；②用全市多个站点的平均数据代表所关注人群的暴露水平. 这两种方法均存在较大的误差和不确定性.

为解决上述问题，国内外学者通常使用数值模拟、空间插值、遥感反演、LUR (Land Use Regression)模型等方法对有限固定站点的污染物监测浓度进行空间化[6]. 在数值模拟方面，Buonocore等[7]使用CMAQ模型模拟了美国电厂排放的PM2.5对人体健康的影响；Arunachalam等[8]使用CMAQ模型模拟了美国机场飞机起飞和降落时排放的PM2.5对人体健康的影响；CHEN等[9]使用CMAQ模型模拟了华北地区ρ(PM2.5)的空间分布和区域传输特征. 在空间插值方面，Pearce等[10]使用Kriging(克里金插值)方法研究了Cusco地区ρ(PM2.5)的空间分布特征；Sampson等[11]使用Kriging方法预测了美国地区ρ(PM2.5)；ZOU等[12]从多角度对比了基于Kriging模型和基于土地利用回归(LUR)模型的ρ(PM2.5)空间分布特征. 在遥感反演方面，WANG等[13]基于卫星遥感获得了Montreal地区高分辨率的ρ(PM2.5)空间分布；Kloog等[14]基于卫星遥感AOD数据反演了新西兰地区ρ(PM2.5)并评价其暴露水平；HE等[15]基于卫星遥感数据获得了中国东部地区长时间系列的ρ(PM2.5). 在LUR模型方面，Jeanette等[16]基于LUR模型预测了美国地区基于面源和道路源的ρ(PM2.5)空间分布；Ho等[17]基于LUR模型预测了韩国地区颗粒物及其化学组分的空间分布；Moore等[18]使用LUR模型预测了洛杉矶地区的ρ(PM2.5)及空间分布.

上述方法均存在一定的不足，如数值模拟方法需要依赖高精度的大气污染物排放清单和高性能运算资源，卫星遥感方法难以解决有云遮挡的数据缺失问题，LUR方法对输入基础数据的要求较高，包括高精度的气象数据、人口数据、污染源排放清单数据、地形数据等资料，数据的可获取性较差. 因此，该研究拟以保定市作为京津冀地区试点城市，进行空气污染采样监测，开展站点代表性和空间预测模型适用性的评估，旨在获取科学有效且可操作性较强的适合中国地区的污染物浓度空间预测模型，为开展精细化大气污染物人体健康暴露评估提供有力支撑.

1 研究方法

1.1 监测点位及监测方法

在河北省保定市选择了13个点位开展空气污染监测，点位布设以位于保定市区的河北大学为中心点，在东、南、西、北4个方位每隔3 km左右设置一个监测点位(见图1). 采样时间为2018年1月3—18日，采样期间空气质量包括4个等级：良(4 d)、轻度污染(3 d)、中度污染(4 d)和重度污染(4 d).

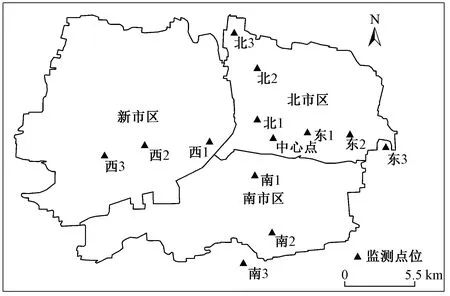
图1 保定市监测点位分布Fig.1 Locations of the monitoring sites in Baoding

每个点位在线监测SO2、NO2、O3、CO、PM10和PM2.5等6项常规污染物监测数据，并采集PM2.5滤膜和VOCs苏玛罐. 在线设备采用中国环境科学研究院自行研发生产的集成传感器专利产品，主要部件为英国阿尔法传感器. 颗粒物监测原理为光散射方法，气态污染物监测原理为电化学方法. 经过清华大学建筑环境检测中心的测试，该传感器对6项污染物的监测结果与美国进口的TSI品牌传感器监测结果的相关系数达到0.92，相对误差为8%，仪器间平行度为98%. 采集过程中设定时间分辨率1 h. PM2.5滤膜采样使用SKC品牌采样泵和采样头采集，使用Whatman品牌37 mm滤膜，每个点位采集石英膜和特氟龙膜各1张. VOCs使用ENTH品牌苏玛罐采集. 在线设备为24 h连续监测，PM2.5滤膜每天采集23 h，VOCs为每天12：00采集瞬时样品. 在实验室分析中，PM2.5组分中的水溶性离子、OCEC和元素分析分别使用离子色谱仪(ICS-600, Dionex, USA)、热光碳分析仪(RT-4, Sunset Lab, USA)和波长色散X射线荧光光谱仪(XRF-1800, 岛津, 日本)，苏玛罐VOCs样品使用气相色谱质谱联用仪(GC-MS)(Nexis GC-2030, 岛津, 日本)进行分析. 在实验室分析的质保质控方面，各物种检测规范必须严格遵守国家相关标准规范，至少设置10%的空白样和平行样，标准曲线相关系数大于0.999[19].

1.2 数据处理方法

对于SO2、NO2、O3、CO、PM10和PM2.5等6项常规污染物监测数据，时间分辨率为小时，使用监测时段内小时数据的平均值获得点位均值. 对于PM2.5组分监测数据，使用23 h采样时长的平均值作为日均值，使用监测时段内日均值的平均值获得点位均值. 对于VOCs监测数据，使用每天12：00采集的瞬时值作为日均值，使用监测时段内日均值的平均值获得点位均值.

注：虚线表示中心点浓度.图2 不同点位φ(SO2)、φ(NO2)、φ(CO)、φ(O3)Fig.2 Concentrations of SO2, NO2, CO and O3 at different sites

2 结果与讨论

将12个点位的各污染物监测浓度与中心点浓度进行对比，该研究中认为各方向上污染物平均浓度与中心点浓度的绝对误差的平均值与中心点浓度的偏差不超过20%时，说明中心点浓度可以代表此点位的浓度.

2.1 不同气态污染物差异性比较

表1和图2显示了不同点位φ(SO2)、φ(NO2)、φ(CO)、φ(O3)以及与中心点的浓度差异. 对φ(SO2)来说，点位1(指各方向的第一个点位，下同)、点位2与中心点的浓度差均在20%以下，点位3与中心点的浓度偏差较大，在40%左右，特别是南3和西3两个点位，其浓度明显高于中心点. 对φ(NO2)来说，整体规律与φ(SO2)类似，点位1、点位2与中心点的浓度偏差均低于20%，点位3与中心点的浓度偏差高于20%，φ(NO2)较高的是北3和东3两个点位. 对φ(CO)和φ(O3)来说，不同点位之间的浓度偏差没有明显差异和规律性，且均小于20%.

表1 各点位污染物浓度与中心点浓度的差异

2.2 不同点位ρ(PM10)、ρ(PM2.5)及其主要组分差异性比较

表2和图3显示了各点位ρ(PM10)、ρ(PM2.5)与中心点的浓度差异，二者变化规律较为一致，即点位1、点位2与中心点的浓度偏差均在20%以下，点位3与中心点的浓度偏差均高于20%. 特别是ρ(PM10)，点位 3的浓度明显高于中心点，ρ(PM2.5)空间分布更为均匀.

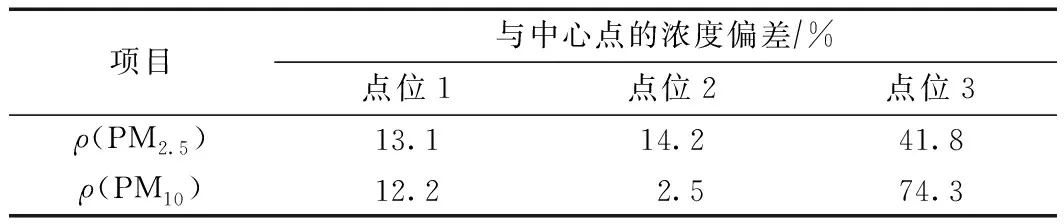
表2 各点位颗粒物浓度与中心点浓度的差异

注：虚线表示中心点浓度.图3 不同点位ρ(PM10)和ρ(PM2.5)Fig.3 Concentrations of PM10 and PM2.5 at different sites

选取PM2.5组分中占比较高的SO42-、NO3-和NH4+[20]开展研究. 表3和图4显示了各组分浓度与中心点的浓度差异.ρ(SO42-)和ρ(NH4+)的变化规律较为一致，即点位1、点位2与中心点的浓度偏差均低于20%，点位3的浓度偏差高于20%. 对于ρ(NO3-)来说，各点位浓度分布较为均匀，浓度偏差均低于20%. 综上，对于ρ(SO42-)和ρ(NH4+)而言，监测点位的代表性为6 km左右；对于ρ(NO3-)而言，监测点位的代表范围更大.

综合来看，对于颗粒物及其大部分组分而言，监测点位的代表性为5～6 km.

表3 各点位颗粒物组分浓度与中心点浓度的差异

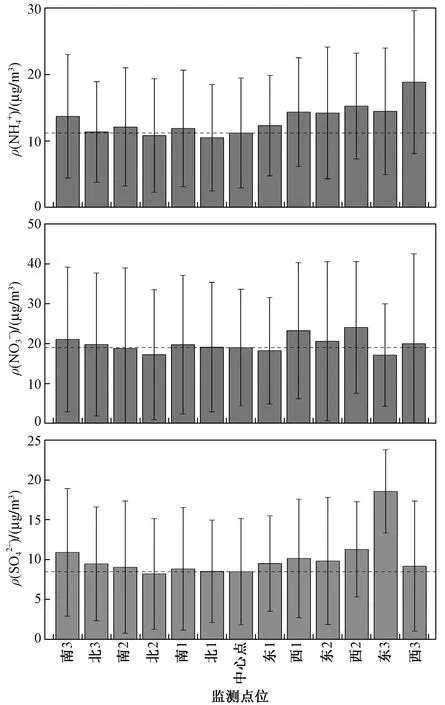
注：虚线表示中心点浓度.图4 不同点位PM2.5中ρ(SO42-)、ρ(NO3-)和ρ(NH4+)Fig.4 Concentrations of SO42-, NO3- and NH4+ in PM2.5 at different sites

2.3 不同点位φ(VOCs)差异性比较

图5显示了各点位φ(VOCs)与中心点的浓度差异. 点位1、点位2、点位3与中心点的浓度偏差分别为17.5%、5.6%、10.0%，表明不同点位φ(VOCs)有所差异，但整体来看，各点位φ(VOCs)与中心点的平均浓度偏差维持在20%以内.

注：虚线表示中心点浓度. 图5 不同点位φ(VOCs)Fig.5 Concentrations of VOCs at different sites

2.4 5 km以外的污染物浓度预测方法对比

该研究得出，对于PM2.5等主要污染物来说，监测点位具有5 km左右的代表性. 根据生态环境部发布的《环境空气质量监测规范》(试行)[21]中的建议，空气质量监测点位的空间代表性一般为500～4 000 m，与笔者所得结论较为一致. 由于目前我国的空气质量监测网络尚比较落后，并没有实现每隔5 km都设有一个监测点位[22]，因此在5 km以外没有监测点位的区域，需要寻求其他方法来获得空气污染物的浓度. 该研究中选取了国内外研究中常用的Radial Basis Functions (径向基函数，RBF)、Local Polynomial Interpolation(局部多项式插值，LPI)、Inverse Distance Weighting(反距离权重插值，IDW)、Kriging(克里根插值)、Kernel Smoothing(内核平滑插值，KS)和Diffusion Kernel(内核扩散插值，DK)等6种空间分析方法[23-26]，在保定市开展污染物浓度插值和验证，选取准确率最高的方法. 使用13个点位中的中心点、点位1和点位3进行插值，使用点位2进行验证，即提取空间插值的点位2的污染物浓度与监测实况进行对比. 该研究以ρ(PM2.5)为例进行分析.

2.4.1RBF方法

表4和图6显示了基于RBF方法的ρ(PM2.5)预测值和监测值的差异，可以看出，该模型预测的浓度高值区在研究区域的东南侧，低值区集中在研究区域的中心位置，研究区域西侧预测的ρ(PM2.5)处于中等水平. 提取4个点位浓度进行比对发现，模型对各点位ρ(PM2.5)的预测值偏高，其中南2点位的绝对偏差最小，为7.9%，西2点位的绝对偏差最大，为26.1%，4个点位的平均绝对偏差为17.9%.

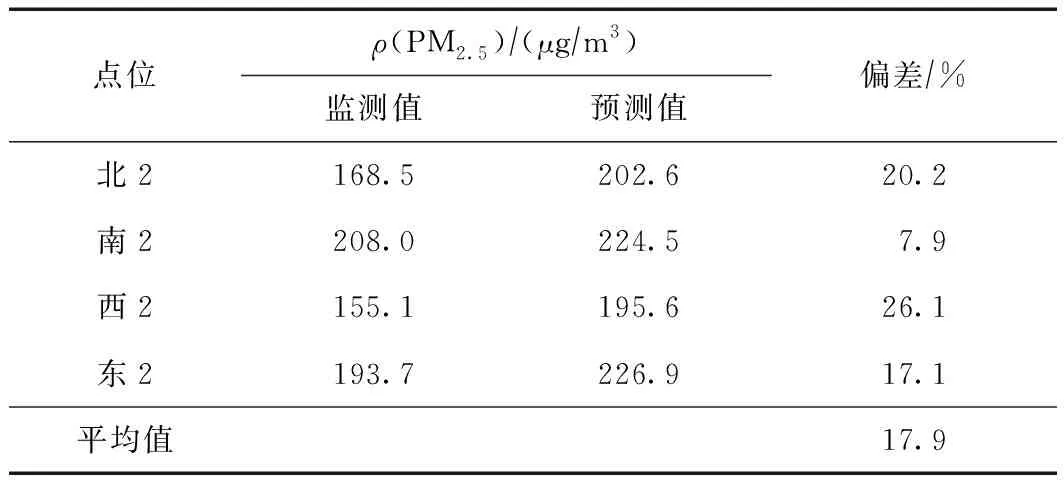
表4 基于RBF方法的不同点位ρ(PM2.5)预测值与监测值的差异

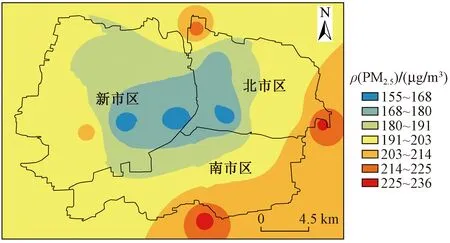
图6 基于RBF方法的空间插值Fig.6 Spatial interpolation based on the RBF method

2.4.2LPI方法

表5和图7显示了基于LPI方法的ρ(PM2.5)预测值和监测值的差异，可以看出，该模型预测浓度的低值区集中在研究区域的中心位置，随着距离向外扩散预测浓度有所升高，高值区集中在研究区域的边界位置. 提取4个点位浓度发现，模型对北、南、西点位的ρ(PM2.5)预测值偏高，对东侧点位的预测值偏低，其中东2点位的绝对偏差最小，为7.8%，西2点位的绝对偏差最大，为13.7%，4个点位的平均绝对偏差为11.2%.

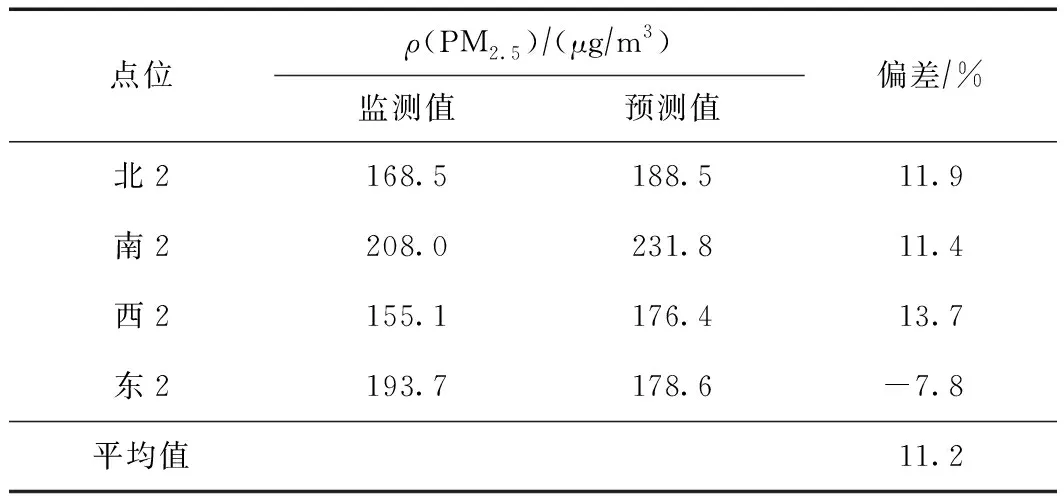
表5 基于LPI方法的不同点位ρ(PM2.5)预测值与监测值的差异

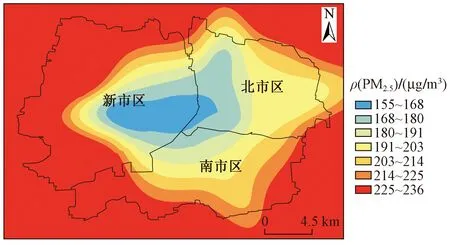
图7 基于LPI的空间插值Fig.7 Spatial interpolation based on the LPI method

2.4.3IDW方法

表6和图8显示了基于IDW方法的ρ(PM2.5)预测值和监测值的差异，可以看出，该模型预测的浓度高值区集中在研究区域南侧、东侧和北侧的3个点位周边，低值区集中在研究区域的中心位置. 提取4个点位的浓度发现，模型对北、西、东点位的ρ(PM2.5)预测值偏高，对南侧点位的预测值偏低，其中东2点位的绝对偏差最小，为9.9%，南2点位的绝对偏差最大，为18.4%，4个点位的平均绝对偏差为12.1%.

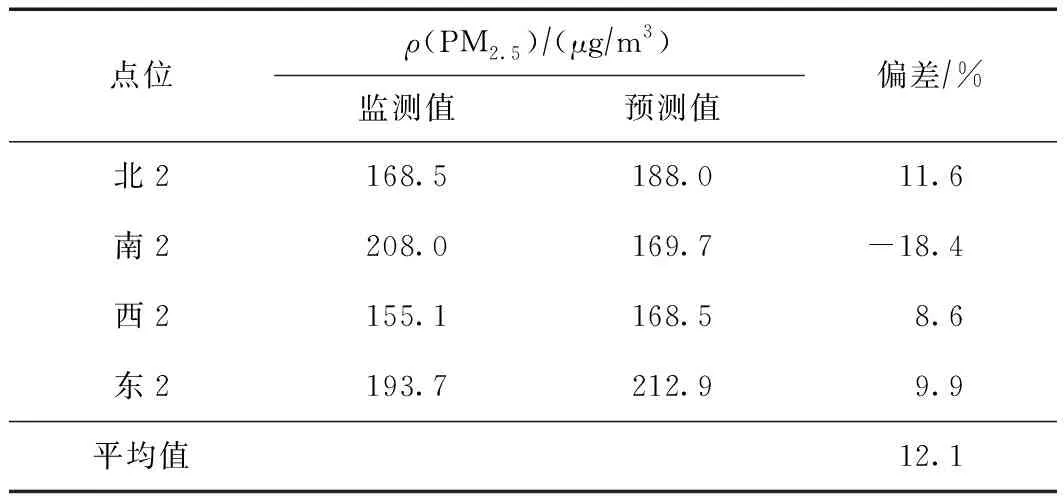
表6 基于IDW方法的不同点位ρ(PM2.5)预测值与监测值的差异

图8 基于IDW方法的空间插值Fig.8 Spatial interpolation based on the IDW method

2.4.4Kriging(克里根插值)

表7和图9显示了基于Kriging方法的ρ(PM2.5)预测值和监测值的差异，可以看出，该模型预测的中心位置浓度最低，东侧和南侧浓度最高，其他区域浓度空间分布较为均匀. 提取4个点位的浓度发现，模型对北、西、东点位的ρ(PM2.5)预测值偏高，对南侧点位的预测值偏低，其中北2点位的绝对偏差最小，为7.7%，西2点位的绝对偏差最大，为15.0%，4个点位的平均绝对偏差为9.3%.

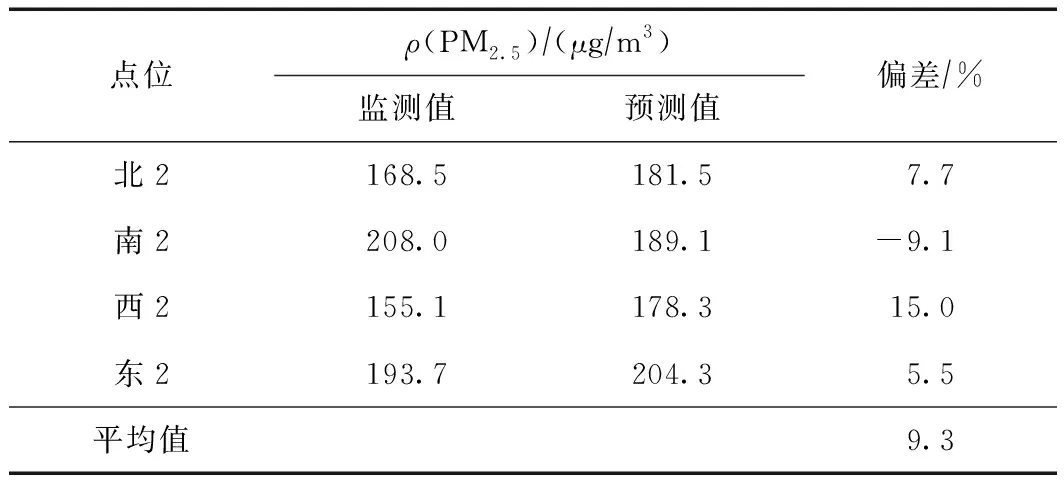
表7 基于Kriging方法的不同点位 ρ(PM2.5)预测值与监测值的差异

图9 基于Kriging方法的空间插值Fig.9 Spatial interpolation based on the Kriging method

2.4.5KS方法

表8和图10显示了基于KS方法的ρ(PM2.5)预测值和监测值的差异，可以看出，该模型预测浓度的高值区处于研究区域的南侧、东侧和北侧，低值区位于中心位置偏西的区域. 提取4个点位的浓度发现，模型对各点位的ρ(PM2.5)预测值偏高，其中南2点位的绝对偏差最小，为4.3%，西2点位的绝对偏差最大，为13.7%，4个点位的平均绝对偏差为10.4%.

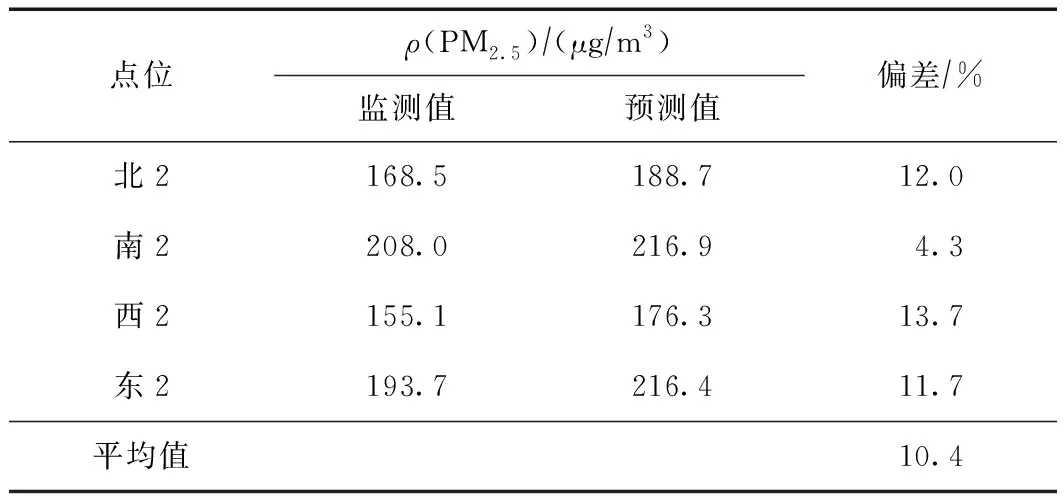
表8 基于KS方法的不同点位ρ(PM2.5)预测值与监测值的差异

图10 基于KS方法的空间插值Fig.10 Spatial interpolation based on the KS method

2.4.6DK方法

表9和图11显示了基于DK方法的ρ(PM2.5)预测值和监测值的差异，可以看出，该模型预测的浓度空间分布呈现自西北部向东南部依次升高的趋势，中间区域浓度分布较为均匀. 提取4个点位的浓度发现，模型对北、西、东点位的ρ(PM2.5)预测值偏高，对南侧点位的预测值偏低，其中东2点位的绝对偏差最小，为5.8%，西2点位的绝对偏差最大，为21.7%，4个点位的平均绝对偏差为12.0%.

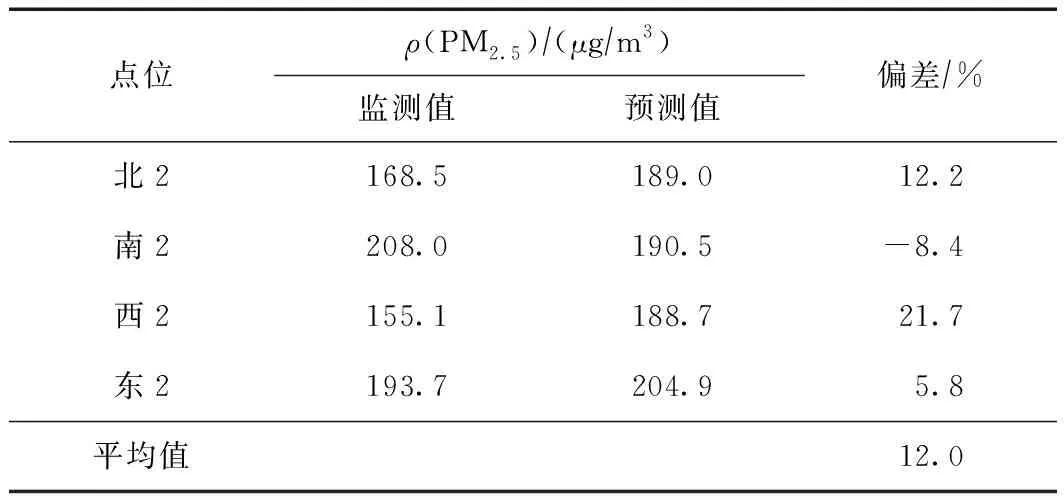
表9 基于DK方法的不同点位ρ(PM2.5)预测值与监测值的差异

图11 基于DK方法的空间插值Fig.11 Spatial interpolation based on the DK method

2.5 研究结果的适用性

该研究选取了京津冀地区污染较为严重的保定市作为研究对象，以河北大学校区为中心点位，每隔3 km在南、北、东、西方向布设采样点，避免了显著常年主导风向(东南风向)的影响. 试图通过密集布点并同时采样、分析的方法，考察大气中主要污染物在与中心点位间不同距离下的浓度差异. 研究通过对各点位气态污染物、颗粒物(PM2.5和PM10)以及PM2.5中主要组分的浓度差异性比较发现，对于SO2、NO2、颗粒物及其组分来说，距离不超过6 km点位的浓度与中心点浓度偏差均小于20%，在6 km以上时其偏差均大于20%，空气质量监测点位的代表性在一般为5～6 km；对于CO、O3和VOCs来说，不同地区其浓度的空间分布更为均匀，各点位与中心点的浓度偏差均小于20%，监测点位的代表性范围更大. 该结果与基本科学认知相符：在冬季，SO2、CO、VOCs以及颗粒物与一次排放关联性较大，因此在小范围区域内具有较好的一致性；而对于O3、NO2、PM2.5中的硝酸盐，则因其主要来自于二次生成，在较大范围内具有一致性.

为了解决6 km内无监测站点情形下大气污染物浓度水平的估算，该研究进行了6种空间分析方法对ρ(PM2.5)预测值的比较研究，结果表明，基于Kriging的空间分析方法对保定市ρ(PM2.5)的预测效果最好，预测值和监测值的偏差小于10%，小于其与中心点位之间的偏差，可以用于估算监测点位6 km以外没有其他监测站点区域的空气污染物浓度. 考虑到一定的保险系数和实际应用中的使用习惯，该研究将6 km人为确定为5 km.

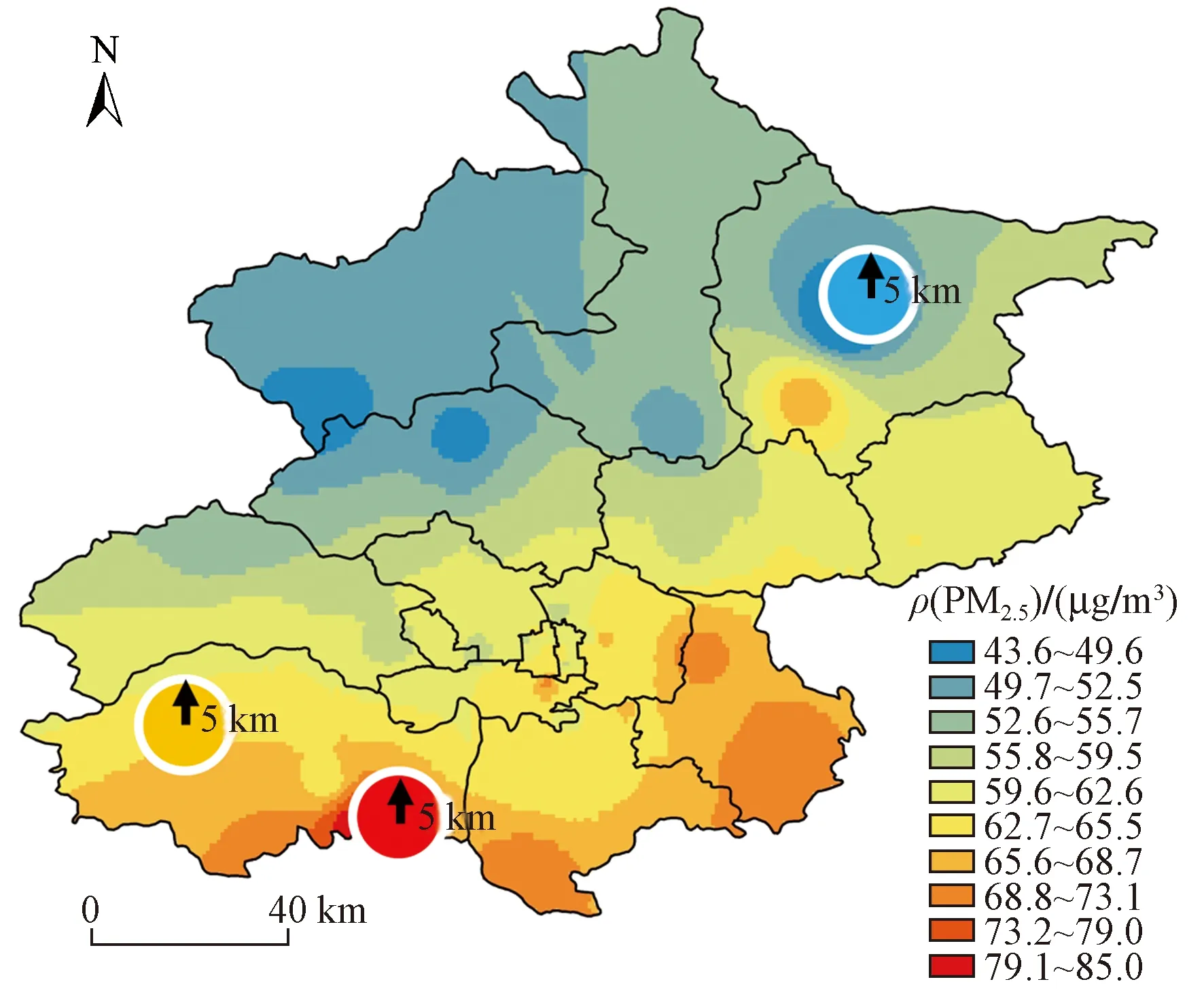
注：5 km以内用监测站点浓度代替，5 km以外使用Kriging方法插值.图12 应用综合方法在北京市进行大气污染物浓度预测的结果Fig.12 The sketch map of spatial distribution of air pollutants in Beijing based on the comprehensive method

该研究结果表明，在进行某城市大气污染物暴露水平研究时，如果人群聚集范围在监测点位周边5 km 以内的区域时，可直接使用该站点的监测数据，监测点位周边5 km以外的区域可使用基于Kriging的空间分析方法获得，图12为以该方法在北京市进行应用的示意图. 另外，该研究是基于冬季相对污染较为严重的北方城市的实测和模型模拟，从污染物排放和大气化学反应的规律考虑，研究结果可能更适合于冬季的北方城市. 今后将在更多城市和不同季节进行相关研究.