基于路由选择的城市道路车辆转向换道区域设置

原志路， 张宜坤， 贾洪飞， 贺 彪

(1. 深圳大学 智慧城市研究院， 广东 深圳 518060； 2. 公安部交通管理科学研究所， 江苏 无锡 214151； 3. 吉林大学 交通学院， 吉林 长春 130022)

车辆的换道行为是常见的交通现象，交通流运行状况在很大程度上受车辆换道行为的影响，尤其在某些交通量较大的路段，频繁的换道增加了车辆总的行程时间，也降低了车辆通行效率及安全性.因此，制定合理的车辆换道策略，引导车辆高效运行是交通流研究领域迫切需要解决的问题.

科学制定道路的限速以及换道控制策略，对于城市路网的运行效率有显著提升效果[1-3].现有针对换道策略的研究或是对路径规划的研究，其共同目的都是使换道车辆(车队)在满足换道约束条件的前提下完成车道变换，换道大部分都是在动态环境下实现的.车辆换道策略的制定则是基于换道模型及路径引导的研究[4].国内外对于路径引导方面的研究，根据路径引导的实时性可分为静态路径引导和动态路径引导2类，其主要实现形式包括预定路径、循迹路径和自规划路径3类，应用场景也主要针对于多条路段或区域路网[5-6].而局部路径规划则是通过传感器测得障碍物与车辆的位置关系，然后再进行实时的路径规划，它是建立在动态规划的环境中，即在一定条件下完成车辆换道行为，实现路径转换.此时的换道行为相对随机，即换道时间随机、地点随机，在系统判断出有合适的插车间隙时完成换道，换道次数不受限制.

对于车辆换道行为的研究，目前主要是从驾驶员个人角度出发，模拟驾驶员的换道行为以及受换道规则影响的反应过程，并通过仿真试验检验相关规则的适用性[7-9].NIE J. Q.等[10]提出了一种基于激励的车辆候选换道决策框架，并假定在车间通信条件下实现车辆间的协同换道，仿真结果证明这种方法实现换道过程的稳定性、效率、均匀性和安全性等方面都存在较大的潜力.WANG M.等[11]利用微分博弈理论预测驾驶员换道行为，提出一种适用于自动驾驶汽车的滚动时域控制法，该方法能够在满足安全性和舒适性要求的前提下产生高效的变道方案，通过预测生成最优的未来行驶策略，包括超车、并道和选择安全空间.XU H. L.等[12]提出了一种基于群组的协同驱动策略对车辆的换道过程进行优化，对一些车间距相对近的车辆进行分组，并调整组之间的换道顺序，仿真试验验证了该策略能够在较短的计算时间内获得满意的协调性能，具有一定的实用价值.当路段流量达到某一数量时，对于自由换道的车辆而言，换道获得的速度、空间优势往往只是暂时的，因为自由换道的发生不能解决其行驶的方向性问题，可能部分自由换道车辆在“换入换出”的过程中改变了其在整个路段行驶的便捷性，但同样也存在部分车辆因自由换道暂时实现车速收益而增加了其在整个路段上行程时间的可能.同时，自由换道车辆对目标车道后方来车的影响是必然存在的.

基于路由选择的车辆换道区域设置是从管理者的角度出发，制定车辆换道策略，通过预定路径的方式，使车辆在固定区域完成换道，旨在减少路段车辆换道总次数，规划车辆在区域路网上的行驶路径，从而降低区域路网总体延误，提高通行效率.

1 局部路由换道行为分析

车辆的路由选择决定了其运行的起终点及方向性，体现在路网上是指路径的规划、路段的选择.局部路由是指在某一路段上，车辆在该路段前后2个交叉口的路由选择，表现为车辆在下一交叉口转向与否，即在区域路段上车辆行驶车道的选择.车辆的路由选择在一定程度上影响了其行进过程中的换道行为及换道次数.

广义上讲，车辆换道应用场景可分为有出入口路段、无出入口路段2大类，并具体应用在高速路、快速路及城市干路等特定路段.按照驾驶员意图，将车道变换分为强制车道变换(mandatory lane-changing)和自由车道变换(discretionary lane-changing)2类.

强制换道指车辆具有确定的目标车道，在一定区间内必须实施换道的行为，如匝道的分流、合流或道路事故引起的车辆被动换道，因存在转向换道意图导致的车辆主动换道等.自由换道则是车辆为了得到更好的驾驶体验而产生的换道行为.

文中依据城市路段上车辆是否存在转向换道意图，将仿真场景中的换道行为分为2类：存在转向换道意图导致发生换道行为的称为转向换道，主要是因路由选择而必然发生的必然性换道行为；其他换道行为统称为随机换道，产生这种换道行为的原因是驾驶员试图获得更快的行驶速度或更大的行驶空间.

在城市道路上，车辆当前行驶车道与其目标车道不一致时，则必然以转向或随机的方式发生换道行为，换道行为发生的数量、位置、方式(转向或是随机换道行为)都将对路段交通流产生较大影响.

2 换道区域设置方案

2.1 车辆换道过程

方案根据初定车道数、各车道流量、速度及左转比例的不同，给出各换道区域最佳设置长度，并结合车辆可变限速设定，以预定路径的方式实现车辆基于路由选择的静态路径规划策略.

选择城市道路双向6车道(单向3车道)建立仿真场景，规定车辆行驶方向的最右侧车道为1车道，1车道为直右车道，2车道为直行车道，3车道为左转车道，且各车道均有左转、直行与右转车流.针对上述仿真场景，根据车辆的路由选择，将该路段分为4部分固定换道区域及3段连接路段，路段功能分区示意图见图1.

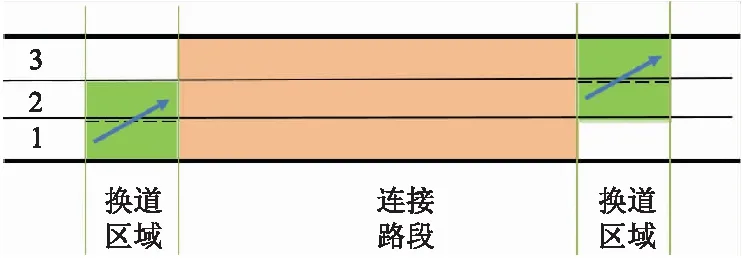
图1 路段功能分区示意图

每部分换道区域的长度根据上游各车道车流的速度、密度及转向比例的不同而有所差异.在各换道区域之间的连接路段上，以可变限速及禁止车道变换等方式加以控制，协同局部车流的行驶速度及安全车距，减少车辆的换道次数，从而提升该路段流量下的车辆通行效率.

其中，连接路段可变限速的实施是依托可变限速点的设置来实现的.在车辆完成换道至下一个换道区域之间的路段禁止车道变换，可变限速点分别设置在连接路段的首端及邻近下一个换道区域之前，如图2所示.

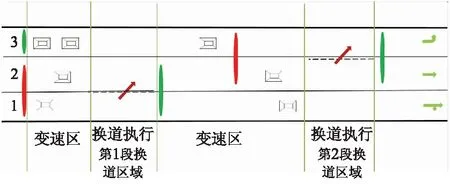
图2 可变限速点设置示意图

图2中红色区域表示减速变速点，车辆经过该点后开始降速行驶；绿色代表提速变速点，车辆经过该点开始提速.图中第1段换道执行区域之前为换道变速区，1、2车道上行驶车辆经过红色区域开始减速，减速至既定车速开始换道，换道结束后车辆在增速变速点增速，在不受其他车道车流影响的前提下保持较高车速行驶.通过期望速度的范围约束调整路段车辆的行驶速度，使得车辆在完成换道后速度在约束范围内有所提升，并在下一换道区域之前恢复至换道准备速度.

连接路段的长度取决于车辆(车流)的期望速度、期望加速度与期望减速度.换道区域连接段最小长度计算式为

(1)

式中：LC为换道区域连接段长度；vE为期望速度；vF为换道完成速度；vP为换道准备速度；aa为期望加速度,aa>0；ad为期望减速度,ad<0.

假定各车道车流均有直行、右转与左转比例，在固定换道区域设置及连接路段设置完成以后，则各车道的车流就有了基于路由选择的静态行驶路径.各车道车流流向分布见表1，根据车辆左右转向顺序，可以将行驶路径分为“先左后右”、“先右后左”2种，静态路径示意图见图3、4.

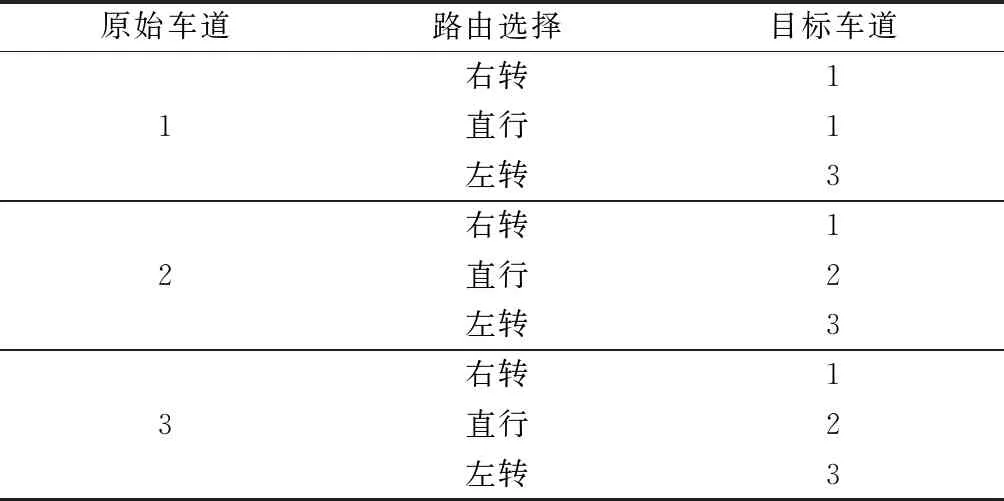
表1 各车道车流流向分布

图3 “先左后右”车辆路径示意图

图4 “先右后左”车辆路径示意图

2.2 仿真参数选取

固定换道区域的长度、连接路段的长度及可变限速点的设置位置等都与仿真参数的选取有直接关系，为了避免因参数选取造成对比试验产生的结论偏差，在仿真场景中车辆及路段的属性应统一取值.VISSIM仿真参数可分为输入参数与输出参数2大类.

2.2.1输入参数选取

2.2.1.1车辆构成

车辆构成可以描述为路段输入车辆中各车型的输入比例，此次仿真试验将车辆车型分为大型车与小型车2类.现实场景中大车运行速度相对小车较慢，或者同类型车辆前后2车速度差距较大，是车辆随机换道现象产生的主要原因.试验中初定大、小车比例为1 ∶9.

2.2.1.2转向比例

各路段初始流量车辆转向比例的大小决定了参与转向换道的车辆数量，而转向换道车辆数也影响了固定换道区域的设置长度.假设1-3车道初始流量分别为a，b，cveh·h-1，各车道流量左转、直行、右转的比例为xp∶yp∶zp，p为车道编号，且xp+yp+zp=1.根据换道策略可得出各区域路段的通过流量，“先左后右”换道策略具体数值见表2.

表2 “先左后右”换道策略区域路段流量

对于因转向换道次序不同产生的2种换道路径控制策略，选择的依据是策略对应的路段最大饱和度xmax，即Vmax/C；对应xmax值较小的则为仿真试验采用的静态规划路径.Vmax是指区域路段最大交通量，“先左后右”换道策略的Vmax值为表2中对应的最大值.

假定各车道的通行能力相同，路段初始流量值相同，即a=b=c，给定一组xp、yp、zp取值，则可求得2种路径对应的最大饱和度，从而确定出相应的静态路径.此次仿真各车道的转向比例取值及最大饱和度见表3，对比选择“先左后右”路径控制策略作为此次仿真场景搭建的基础.

表3 转向比例参数

2.2.2输出参数选取

仿真输出参数用于对比有、无控制策略的仿真效果，包括车辆的行程时间、行驶距离、行驶速度、车辆延误、车道编号、换道次数及车辆的加速度和减速度等.在对比试验数据分析时，统计2种场景下所有车辆的平均行程时间与平均行驶距离，基于此计算不同策略下区域车辆平均行程速度，根据车辆的加速度、减速度分布与行驶车道编号分布，可分析车辆的运行轨迹及车辆换道时对周边车辆的影响.VISSIM输出评价指标见图5.

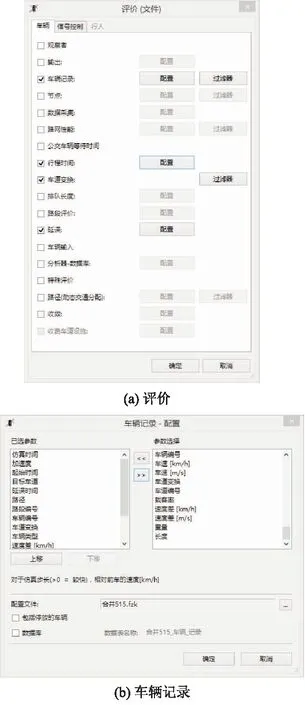
图5 仿真评价输出指标

3 换道仿真场景初建与数据分析

根据固定换道区域的设置个数，将仿真路段分为4段依次进行仿真试验.每一段道路的仿真场景对应的车辆初始速度相同，输入流量及转向比例不同，第2段固定换道区域的输入流量及转向比例的取值取决于上一换道区域的初始流量及转向比例.统计分析各阶段仿真数据，借助MATLAB数据拟合，得出各段换道区域的最佳设置长度.

此次仿真场景以“先左后右”静态路径为基础，且各车道仿真初始流量值相同，根据各车道拟定的转向比例，可以求出4段仿真路段各车道的输入、输出流量及转向比例.

3.1 第1段换道区域设置与数据分析

第1段换道区域部分车辆由1车道左转变道至2车道，准备区长度30 m，恢复区长度20 m，第1段换道区域示意图见图6.

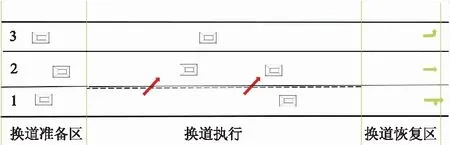
图6 第1段换道区域示意图

各车道初始流量相同，大、小车比例均为1 ∶9，速度v为50 km·h-1，波动范围为48～58 km·h-1.自变量包括换道区域长度L(10 m≤L≤200 m)、输入流量aveh·h-1(50≤a≤1 200)，L每隔5 m取一次值，a每隔50 veh取一次值，其他输入参数见表4.仿真中小型车长度范围为4.11～4.76 m，大型车长度为10.21 m；当L取5 m时，仿真车辆会因车身长度大于固定换道区域长度而在部分路段堵塞不动，因此取Lmin=10 m.

表4 第1段换道区域输入参数

第1段换道区域的仿真场景中，换道车辆不会对3车道车辆产生影响，因此该阶段数据统计分析时只对1，2车道的车辆数据做统计处理.为了方便比较换道区域长度变化对该流量背景下路段行驶车辆的影响，选择路段平均行程速度作为评价指标，由车辆行驶距离与车辆路段平均行程时间求得.

统计初始流量由50增至1 200 veh·h-1、换道区域长度由10增至200 m的仿真数据，汇总结果见图7.

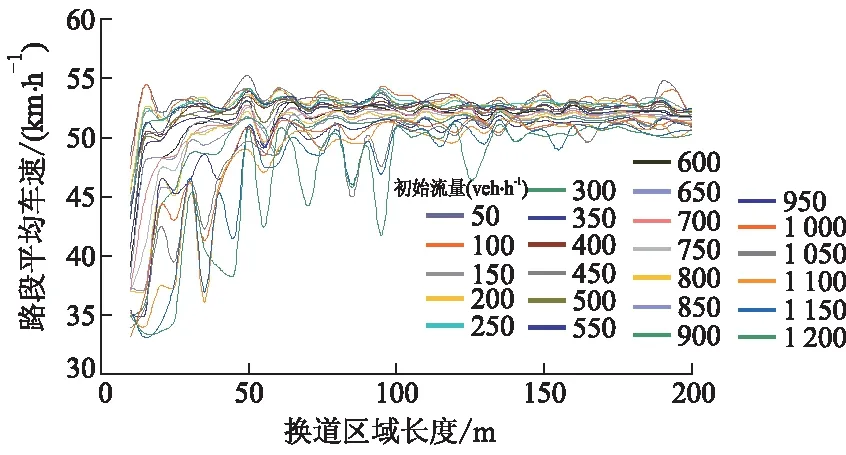
图7 第1段换道区域平均行程速度汇总图

由图7可见，当输入流量一定时，随着固定换道区域长度的增加，路段平均车速趋于稳定；且当换道区域达到一定长度时，初始流量的增加对路段平均车速的影响较小，说明此时的换道区域能基本满足路段车辆的换道需求.

当输入流量在50～800 veh·h-1时趋势曲线波动较小，路段运行较为稳定，说明路段车辆运行状况主要受换道区域长度设置的影响；当输入流量在850～1 200 veh·h-1时趋势曲线波动明显，尤其当单车道流量增至1 000 veh·h-1以上时，平均速度波动幅度增加，说明车辆在该路段运行受交通量影响较大，即交通量是影响路段通行效率的主要因素，而换道区域长度次之.

“先左后右”路径控制策略对应的单车道最大区域交通量为1.4aveh·h-1，且要小于单车道通行能力，城市道路主干路单车道通行能力为1 117 veh·h-1，结合初步仿真试验数据，第1段换道区域的初始流量aveh·h-1确定为800 veh·h-1.根据拟合趋势曲线函数(如图8所示)，求得当换道区域长度L=40 m时，车辆平均速度趋于平缓，由此确定第1段换道区域的最佳设置长度为40 m.

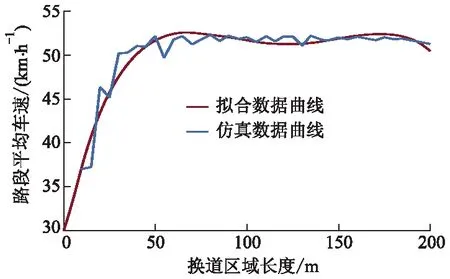
图8 第1段换道区域平均行程速度 变化趋势图(a=800 veh·h-1)

3.2 第2、3、4段换道区域设置与数据分析

第2段换道区域部分车辆由2车道左转变道至3车道，第3段换道区域部分车辆由3车道右转变道至2车道，第4段换道区域部分车辆由2车道右转变道至1车道.输入流量跟转向比例有所变化，大小车比例均为1 ∶9，速度v为50 km·h-1，波动范围为48～58 km·h-1.自变量为换道区域长度L(10 m≤L≤200 m)，L每隔5 m取一次值.其他输入参数见表5.

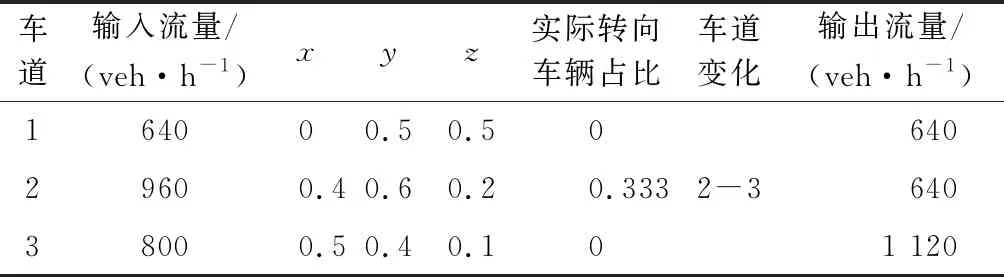
表5 第2段换道区域输入参数

第2、3段换道区域的仿真场景中，换道车辆不会对1车道车辆产生影响，因此该阶段数据统计分析时只对2、3车道的车辆数据做统计处理；第4段换道区域的仿真场景中，换道车辆不会对3车道车辆产生影响，因此该阶段数据统计分析时只对1、2车道的车辆数据做统计处理.根据拟合趋势曲线函数，可求得第2、3、4段换道区域的最佳设置长度分别为45、40、40 m.

4 试验的场景搭建与数据分析

4.1 有控制策略的城市路段仿真分析

各阶段最佳换道区域长度已确定的情况下，建立合并的路段仿真场景，还需要求得连接路段的长度.连接路段长度计算见式(1)，其中换道准备速度、换道完成速度均为50 km·h-1，期望速度为60 km·h-1，期望加速度、减速度为±1 m·s-2，计算求得LCmin=84.88 m,仿真场景中3段连接路段长度均取整LC=100 m.仿真路段示意图见图9.

图9 有控制策略仿真路段示意图

根据得到的各阶段最佳换道区域长度与连接路段长度，结合期望车速设置策略，合并至整条路段(图9).路段全长(565±0.2)m，采用“先左后右”的换道策略，输入参数见表6.统计整条路段车辆数据并加以分析，数据汇总见表7.

该路段所有车辆平均行驶距离565.17 m，平均路段行程时间36.85 s，平均行驶速度55.21 km·h-1，总换道次数167次.

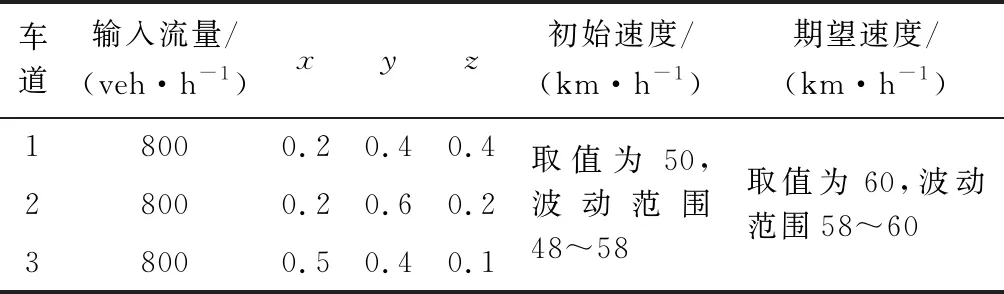
表6 有控制策略仿真路段输入参数

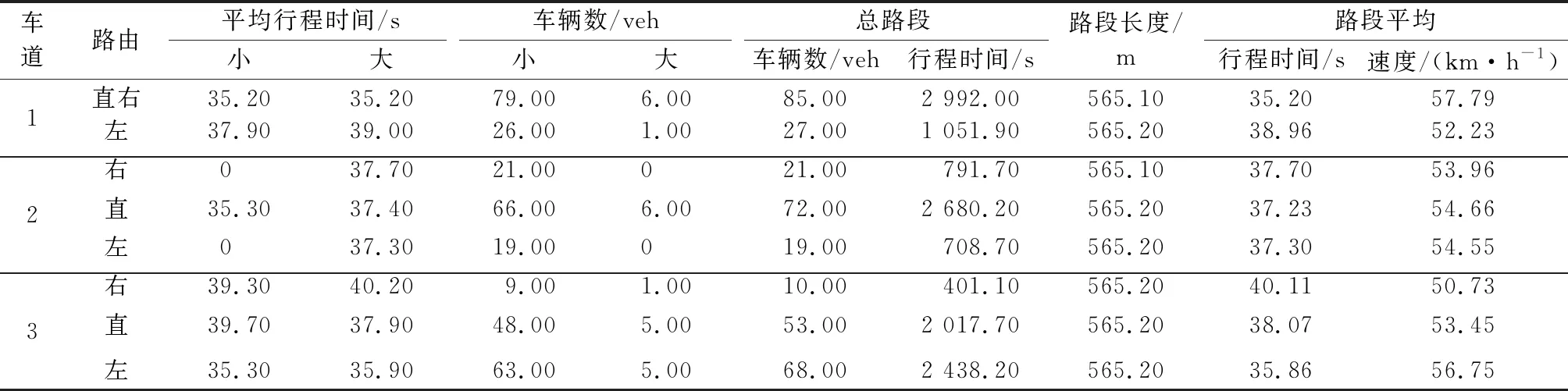
表7 有控制策略仿真路段输出数据

4.2 无控制策略的城市路段仿真分析

无控制策略路段不设置固定换道区域，路段车辆不设置可变限速及静态路径规划策略的约束，车辆换道地点随机、换道时间随机.路段全长(565.0±0.2)m，无换道控制策略，车辆根据仿真场景的跟驰模型与换道模型参数约束行驶，图10为该仿真路段示意图，主要输入参数见表8，该路段车辆换道部分数据汇总见表9.

图10 无控制策略仿真路段示意图

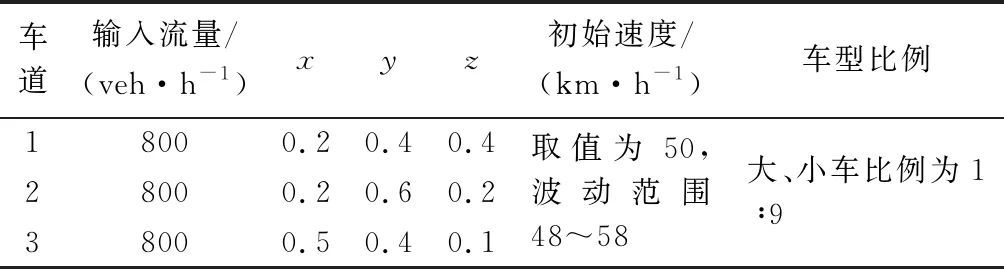
表8 无控制策略仿真路段输入参数

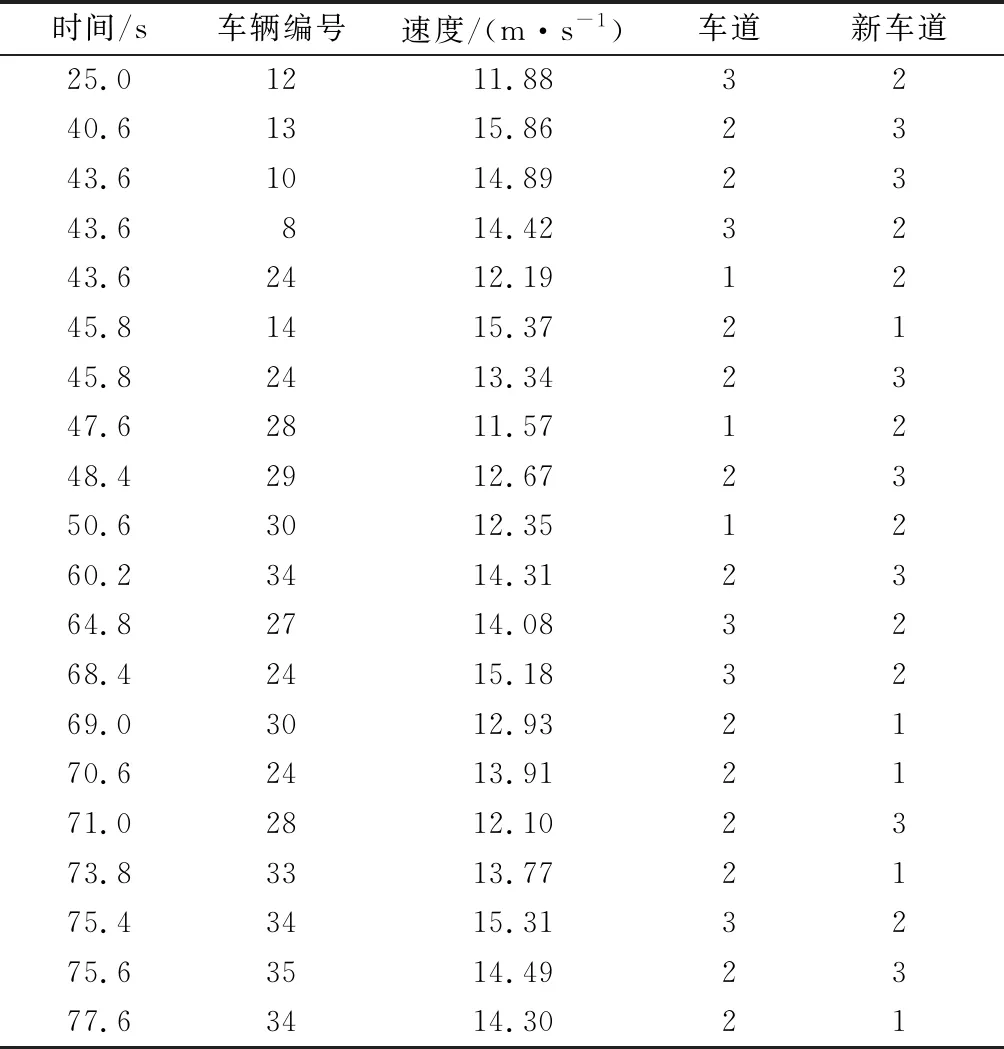
表9 无控制策略仿真路段车辆换道部分数据

该路段所有车辆平均行驶距离565.04 m，平均路段行程时间41.31 s，平均行驶速度49.24 km·h-1，总换道次数273次.

4.3 数据对比与分析

对比有、无控制策略仿真试验数据，绘制基于路由选择的车辆速度对比图，如图11所示.当大小车比例为1 ∶9时，有控制策略的路段相比于无控制策略路段，车辆平均行程速度增加了12.13%，平均行程时间减少了10.80%，换道次数减少了106次.证明固定换道区域设置效果明显，策略有效.

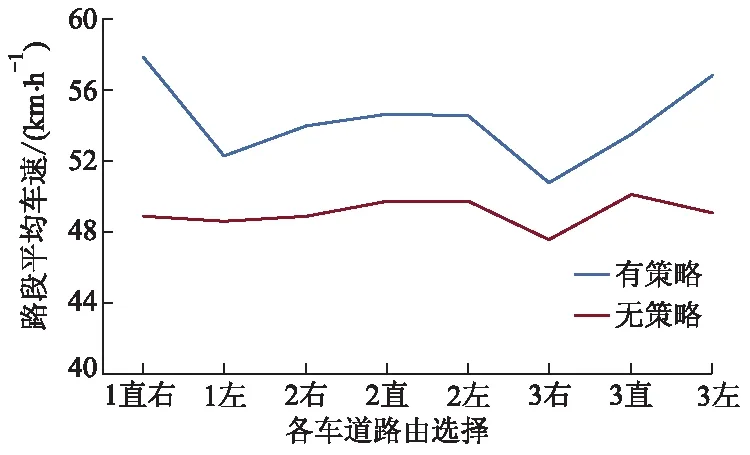
图11 有无控制策略的车辆速度对比图

车辆自由换道是为了获得更大的行驶空间与更快的行驶速度，仿真试验中无控制策略换道次数比有控制策略多了106次，而车辆平均行程时间却有所增加.分析认为，无策略控制时，车辆转向换道很大一部分发生在路段后半段，对前半段利用率低是造成延误增加的一个原因；另一方面，车辆在换入目标车道后，其后方车辆会基于安全车距的判定做出减速与否的行为.

车辆自由换道得到的提速只是暂时的，自由换道的发生并不能解决车辆行驶的方向性问题.可能部分自由换道车辆在“换入换出”的过程中改变了自身在整个路段行驶的便捷性，但同样也存在部分车辆因自由换道暂时实现车速收益而增加了整个路段上车辆总行程时间的可能，此时的换道行为可视为无效换道.

同时，无法保证自由换道车辆顺利换出后能顺利换入，且自由换道车辆对目标车道后方车辆的影响是必然存在的，下面以仿真试验中车辆V84在无控制策略路段上车辆记录数据加以分析.

V84车辆经过2次自由换道，先由2车道换至1车道，行驶一段距离后又换回2车道，换道过程如图12所示.

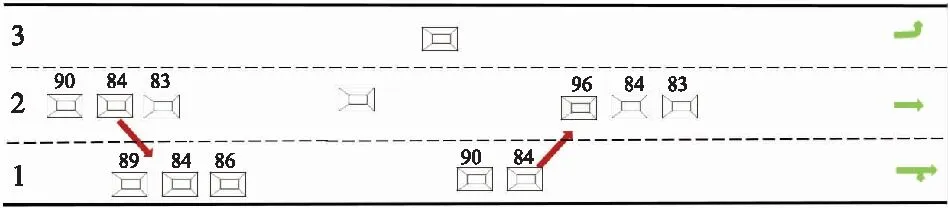
图12 V84换道过程示意图

由图12可见，V84再回到2车道时，仍然处在V83之后，并没有摆脱V83的干扰，同时也对V89、V90、V96产生了影响.车辆速度变化过程如图13所示.

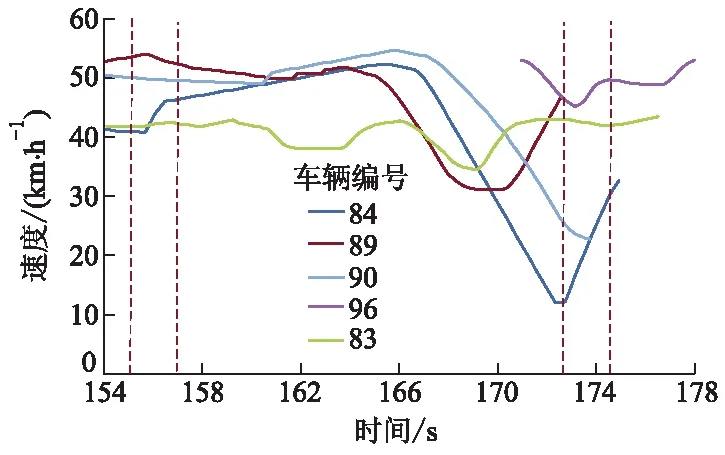
图13 V84及周边车辆速度变化

由图13可见，V84在155.6 s时开始第1次换道，由2车道换至1车道，157.4 s时换道完成.V84换至1车道后速度有所提升，但目标车道后方车辆V89车速受到影响，V89车速降低42.36%.另外，V84在1车道行驶一段距离后，减速寻找换回2车道的可插车间隙，这一过程对其后方车辆V90产生影响，V90车速降低58.21%.还可发现，V84在172.6 s时开始第2次换道，由1车道换回至2车道，174.4 s时换道完成.V84第2次换道行为对目标车道后方车辆V96产生影响，V96车速降低14.70%.

相较于2次自由换道之前的车速，V84在换回2车道后，自身车速降低了31.74%.V84在该路段上的自由换道行为，不仅没有获得更快的速度收益，反而增加了路段上其他车辆的总体延误，其自由换道行为是无效的.

5 结 论

1) 文中基于路由选择的车辆换道控制策略(即合理的换道区域设置、高效的路径引导)能有效减少车辆换道次数，降低因随机换道造成的延误，提高车辆路段平均行程速度，优化区域路网的通行能力，从而提高交通系统的运行效率及安全性.

2) 用“先左后右”静态路径及车辆控制策略的仿真试验仍不能避免车辆换道时对目标车道后方来车产生的影响，尤其当流量增大到一定水平时，固定换道区域没有足够的可穿插间隙，此时车辆若转向换道则必然会使后车降速运行.

3) 此种控制策略只是减少了因部分自由换道车辆无效换道产生的系统延误，提升了车辆在连接路段的通行效率，没有实现车辆间的相互协同.