瞬态工况下DPF温度特性的数值分析

李小华， 程静峰, 仇 滔， 岳广照

(1. 江苏大学 汽车与交通工程学院， 江苏 镇江 212013； 2. 北京工业大学 环境与能源工程学院， 北京 100124； 3. 北京理工大学 机械与车辆学院， 北京 100081)

柴油机因具有输出功率大、燃烧效率高、燃油经济型好等优点，受到广泛关注[1].然而柴油机的颗粒物(PM)排放是同等排量汽油机的30～80倍[2]，极大危害了环境，因而研究如何降低柴油机PM排放具有重要意义.柴油机颗粒捕集器(DPF)是全球公认的最有效的减少柴油发动机微粒排放的后处理装置，其捕集效率超过90%[3-4]，可以极大地降低柴油机的PM排放.常用的DPF通过将排气中的颗粒物捕集在过滤器壁面上来清除颗粒[5].但使用过程中颗粒物的不断累积会导致排气温度积聚，陡峭的温度梯度容易造成热应力失效，破坏DPF结构[6].已知DPF的结构参数会引起内部温度场变化[7]，同时，加载过程所处的工况环境以及颗粒物沉积量对内部的温度分布有重要影响，通过对DPF内部温度场的变化规律进行探究，可以最终达到优化温度分布、降低热应力极值的目的.目前，DPF温度特性的研究主要集中于再生过程，对加载过程的研究较少，且DPF温度模型研究主要集中于固体导热方法[8-9]，关于气体与固体之间的对流传热方法研究较少.费腾等[10]建立了DPF的三维仿真模型，分析了再生条件下DPF载体内温度梯度的分布.文献[8]基于一维进出口通道之间的二维离散化建立了蜂窝壁流式DPF的传热模型，并将该模型应用于具有高热导率载体的设计与分析中.文献[9]采用准一维模型研究了直径、长度和孔密度对稳态条件下再生过程中DPF最高温度的影响.

文中基于上述研究成果，采用有限元原理建立基于瞬态工况对流传热方法的DPF轴向温度计算模型，分析来流流量、载体目数(CPSI)、载体长度、颗粒物沉积量对DPF轴向温度的影响规律，在保证结果准确度较高的前提下提高运算速度，从而为优化DPF结构，降低DPF热损坏风险，延长DPF使用寿命，进一步深入研究DPF工作特性提供参考.

1 模型假设及建立

1.1 模型假设

① 忽略孔道间形状及流体流动的不一致性[11].② 忽略气体分子间的相互作用，将DPF内气体认为是理想气体[12].③ 忽略DPF孔道内部的热传导，忽略与外部环境的热交换[13].④ 忽略DPF内部氧化反应放热过程，将DPF简化为无源的物理捕集器.⑤ 忽略颗粒物在DPF孔道内沉积的不一致性，认为颗粒物在孔道内均匀分布[11].

1.2 DPF温度分析建模

1.2.1DPF轴向气体温度建模

DPF为前后交替封堵的孔道结构[14]，气流流入DPF孔道时，除了沿孔道轴向运动，还经四周壁面向相邻孔道渗透.由于单个DPF孔道的尺寸较小，轴向距离远大于径向距离，因此气流在DPF内部的流动可视为一维管道流动.排气由DPF入口向出口的流动过程使得DPF轴向呈现连续的热量传递过程，然而不同轴向位置在不同时刻又保持相对独立的温度分布，整个温度传递过程符合有限元方法的基本原理，因此文中利用有限元方法建立DPF轴向温度模型.

将DPF沿轴向均匀切分为9个片区，分层结构图如图1所示，单个孔道结构图如图2所示.其中空白处为孔道气体流通面积区域，用Ag表示，阴影为固体横截面区域，用Aw表示.

图1 DPF轴向分层结构图

图2 单个孔道结构图

气体流动过程中气体温度随移动距离变化，孔道内气体温度求解公式[15]如下：

(1)

式中：Tg表示DPF孔道内气体温度，K；x表示片区长度，m；h表示气体与载体之间的对流传热系数，W·(m2·K)-1；C表示单个孔道横截面周长，m；ρg表示气体密度，kg·m-3；Ag表示单个孔道内气体流通横截面积，m2；cp,g表示气体定压比热容，kJ·(kg·K)-1；v表示气体流速，m·s-1；Tw表示载体温度，K.

气体温度因对流传热而改变，为得到同一时刻不同片区内的气体温度，运用隐式欧拉法对式(1)进行空间离散，得到轴向各测点的气体温度方程如下：

(2)

1.2.2DPF载体温度场建模

DPF内部气体损失内能温度逐渐降低，而DPF载体因为得到内能导致温度升高，且随作用时间不同，气体与载体之间的传热强度逐渐变化，DPF载体的温度求解公式如下：

(3)

式中：ρw表示DPF载体密度，kg·m-3；Aw表示DPF单个孔道固体横截面积，m2；cw表示DPF载体比热容，kJ·(kg·K)-1.

为得到单一片区内不同时刻的载体温度，通过显式欧拉法对式(3)进行时间离散，离散后载体温度方程如下：

(4)

1.2.3对流传热系数计算

由于发动机在运行过程中工况变化范围较广，对应的排气流量，排气温度大幅度变化，这些变化都将影响两个求解方程中对流传热系数，因此需要对对流传热系数h进行推导求解.在流体力学中，通常用雷诺数Re表示流体运动状态，将试验工况的相关参数计算雷诺数，发现数值小于临界雷诺数Rec=2 300，可以确定气体在DPF内部孔道的流动属于层流状态.根据齐德-泰勒公式可知，在层流状态下，努塞尔数Nu用式(5)表示，对流传热系数h如式(6)所示.

(5)

(6)

式中：Nuf和Ref表示定性温度下的努塞尔数和雷诺数，定性温度为流体的平均温度；l表示DPF各片区长度，m；d为特征长度，在此为孔道当量直径，m；Pr为普朗特数；μ为动力黏度，kg·(m·s)-1，下标f和w分别表示流体平均温度及壁面温度；λ表示流体的导热系数，W·(m·K)-1.

2 模拟仿真试验

2.1 仿真模型

图3为Simulink仿真模型结构示意图.模型进行计算时，气体温度求解方程和载体温度求解方程均由入口向出口求解.各片区通过气体温度相连接，上一片区气体出口温度为下一个片区的气体入口温度.初始第一片区的气体温度为DPF入口处温度传感器采集到的温度，初始载体温度为环境温度.

图3 Simulink仿真模型结构示意图

2.2 模型验证

为了保证模拟试验的准确程度，需要对DPF温度模型进行验证.试验选用的DPF结构参数：载体材料为堇青石；目数200目；壁厚0.32 mm；直径260 mm；长度270 mm；体积14.3 L.在DPF内部中心轴等距布置9个温度测点获取内部温度，每个测点对应图1中相应片区的中心点.选用的试验工况为典型的加速和减速过程，具体的变化过程如下：从A25工况(1 213 r·min-1,330 N·m)升至B75工况(1 825 r·min-1,1 022 N·m)再降至A25工况，测试持续时间为500 s，初始碳烟量为0.

DPF温度模拟值与试验值对比如图4所示.在温度上升过程，DPF前端、中部及后端位置模拟值与试验值吻合程度较高，最大误差为8.1 K；在温度下降过程，3个位置模拟值与试验值吻合程度较差，温度误差在12.5 K左右，且集中于温度下降初始阶段，在温度下降后期吻合性较好.从图4中可以发现，计算值温度下降速度要快于试验值温度下降速度，这是由于模型忽略了DPF载体自身的固体热惯性，将DPF载体温度的连续下降简化为瞬时下降，缩短了温度变化时间.由于在初始阶段，气体与载体温差较大传热较强，载体降温速率较大，因此仅在起始位置误差较大，在后期误差逐渐缩小.模拟值与试验值基本吻合，最大数据误差在10%以内，认为建立的温度模型能够反映DPF温度的实际情况.

图4 DPF温度模型计算值与试验值对比

3 试验结果分析

采用仿真模型研究各个因素对DPF轴向温度的影响规律.仿真可变参数为：流量173～1 072 kg·h-1；载体孔目数100～300目；载体长度270～360 mm；颗粒物沉积量1～8 g·L-1.通过分析相关表征参数，得到DPF载体温度特性的评价.将模型的9个片区编号为1#-9#，入口端为1#，出口端为9#，定义1#与9#达到相同温度之间的最大迟滞时间为tmax.轴向相邻片区之间温度差与间距的商为轴向温度梯度，用(dT/dx)i-j表示，其中i表示前一片区编号，j表示后一片区编号.图5显示了DPF轴向各区域温度梯度变化.由图5可知，(dT/dx)1-2的轴向温度梯度曲线最高，可推断，DPF载体因热冲击造成结构破坏多发生于入口处，此结论与费腾等[10]研究较为一致，因此文中取tmax、(dT/dx)1-2进行温度特性分析.由于载体升温过程和降温过程原理类似，且升温过程的最大温度梯度高于降温过程，为降低测试点密度，增强图表可读性，后续试验仅探究升温过程载体的温度特性.

图5 DPF轴向各区域温度梯度

3.1 流量对DPF载体温度特性的影响

在来流流量分别为173、371、587、813和1 072 kg·h-1，入口温度从438 K升至677 K，初始碳烟量为0条件下，模拟DPF加热过程.不同流量下载体温度和升温速率的变化情况如图6所示.由图6a可知，来流流量由173 kg·h-1增加至1 072 kg·h-1，9#温度-时间曲线逐渐向前推移，tmax由41 s降低至14 s且下降速率逐渐减小.这是因为载体温度升高来自于排气的热量传递，在排气进入载体的初始时刻，排气与载体的温差达到最大，对流传热最强，载体升温速率最大；随着载体温度升高，排气与载体之间温差降低，对流传热减弱，载体升温速率逐渐减少，当排气与载体温度相等时，对流传热近似为0，升温速率趋近于0，导致载体的温度-时间曲线为一条持续上升且上升速率逐渐减少的曲线.排气从入口至出口的沿程不断发生热交换，到达出口时与载体温差达到最低，对流传热最弱，升温速率最低，载体入口和出口虽然在同一起始点开始升温，但是入口升温速率大于出口，导致升温曲线存在滞后.然而，流量的增加只能加快载体升温，无法改变载体入口先受热升温，后端再受热升温的整体顺序，即增大流量并不能使载体各部分同步升温，必然存在迟滞时间和轴向温度梯度.因此当流量持续增加，tmax的下降速率不断减小并向0趋近.由图6b可知，在第50 s时，9#的升温速率随来流流量增加而增加，这是由于来流流量增加导致气体流速加快，对流传热增强，载体升温速率增加；在第100 s至150 s内，9#的升温速率随流量的增加而减小，原因是前期载体温度快速上升导致温差降低，对流传热减弱，升温速率减少；在第200 s之后，9#的升温速率达到近似相等的水平并渐趋近于0，这是因为载体完成整体的升温过程，与气体温差进一步降低，对流传热持续减弱并最终趋于0.

图6 不同流量下温度及升温速率随时间的变化

不同流量下载体入口处温度梯度变化如图7所示.由图7可知，(dT/dx)1-2曲线在升温初始时刻迅速上升，在第44 s附近达到最高点，之后以较快的速度下降，且随时间增加下降速率逐渐减少，靠近350 s时趋近于0.这是因为在升温初始时刻，载体入口受到高温排气直接热冲击，气体与载体之间的强烈温差使得对流传热显著增强，载体入口升温迅速，后续载体没有直接遭受高温冲击，对流传热相对温和，升温速率较慢，导致入口载体和后续载体在初始时刻形成较大温度梯度.随着时间增加，入口载体与气体温差减小，对流传热减弱，后续载体对流传热增强，温度升高且升温速率增加，轴向温差减小，导致温度梯度逐渐降低并趋向于0.来流流量为173、371、587、813和1 072 kg·h-1时，(dT/dx)1-2极值分别为1 449.62、1 082.29、875.94、740.75和635.00 K·m-1，最大降幅达到56.2%.随来流流量增加，(dT/dx)1-2极值降低且下降速率不断减少，持续时间减少，上述结论与孟忠伟等[16]的研究较为一致，根据研究显示，流量增加使得载体温度梯度呈下井趋势，有助于载体传热.这是由于增加流量加速了载体孔道内气体流动，对后续载体对流传热的增强作用尤为显著，使载体升温加速，降低温度梯度，减少温度梯度的持续时间.通过研究不同流量对DPF温度特性的影响可知，流量增加提高了气体的流速，增加了热量的基数，从而加剧了对流传热，导致载体在更快的升温速率下完成升温过程.因此在实际应用中应选择合理的排气流量，尽可能降低DPF升温的迟滞时间，从而加速整个载体的升温过程使DPF尽快达到热平衡状态，减小DPF受到的热应力冲击，改善后处理系统可靠性.

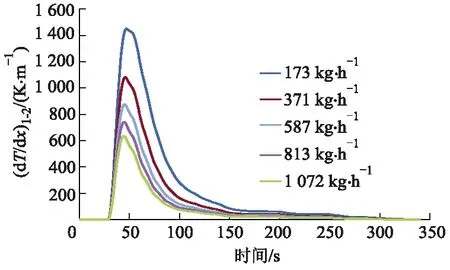
图7 不同流量下温度梯度随时间变化

3.2 孔目数对DPF载体温度特性的影响

设定DPF孔目数分别为100、150、200、250和300目，排气流量恒为173 kg·h-1，模拟DPF加热过程，如图8所示.由图8a上图可知，孔目数由100增加至300目,tmax由52 s降低至32 s，迟滞时间线性降低.这是因为孔目数增加使得载体的过滤面积成倍增加，同等加热条件下载体更容易快速升温，传热性能线性增强，加速升温过程.由图8b可知，在第50 s时，300目DPF载体升温速率最高，100目载体升温速率最低，升温速率随孔目数增加而增加；在第100 s至第250 s范围内，升温速率变化规律相反，孔目数越高，升温速率越低；在第250 s之后各载体升温速率差别较小.随着时间增加，升温速率随孔目数变化由增加变为减少，这是由于孔目数较多的载体更早完成快速加热过程，载体温度已升至较高水平，此时孔目数较少的载体处于快速升温阶段，因此载体孔目数与升温速率呈反向关系.在250 s之后，各载体温度均达到较高水平，升温速率相差不大.

不同孔目数下载体入口处温度梯度变化如图9所示.由图9可知，随着孔目数由100目增加至300目，(dT/dx)1-2极值分别为1 619.32、1 531.66、1 465.89、1 398.65和1 326.43 K·m-1，呈线性下降趋势且持续时间减少.这是由于载体孔目数增加，过滤面积线性增加，相同时间有更多内能由气体传递至载体，加热入口的同时更加快速地加热后续载体，导致载体温差减小，温度梯度线性降低；同时传热加快也使温度在更短时间内达到相对稳定，使温度梯度持续时间减少.通过研究载体孔目数对DPF温度特性的影响可知，增加孔目数有利于减少载体温度梯度，加速载体传热，因此在实际应用中应该尽可能增加载体的孔目数或者增加单个孔道的孔径尺寸，从而增加DPF气体流通面积和传热效率，减小再生频率，改善发动机燃油经济性.

图8 不同孔目数下温度及升温速率随时间变化

3.3 长度对DPF载体温度特性的影响

在DPF长度分别为270、360、450、540和630 mm，排气流量恒为173 kg·h-1，孔目数恒为200目条件下模拟DPF温度变化，如图10所示.由图10a可知，载体长度由270 mm增加至630 mm，tmax由42 s线性增加至53 s，从局部放大图上可更直观地看到上述变化.原因是载体长度增加导致体积和总质量增加，达到相同的目标温度需要更多的内能，轴向对流传热减弱，且载体长度增加导致气体流通距离变长，导致在气体在孔道内的迟滞时间线性增加.由图10b可知，在第50 s时，升温速率随载体长度增加而减少；在第100 s至第200 s范围内，升温速率随载体长度增加而增加；在第250 s之后，各载体升温速率基本相同.原因是在初始时刻，长度越长的载体拥有更长的片区长度及更大的片区质量，同等传热条件下升温幅度低于长度较小载体，因此在初始时刻升温速率随载体长度增加而减少；在第100 s至200 s范围内，长度较长的载体拥有更大的温差和更快的传热速率，导致升温速率趋势相反；250 s之后各载体升温速率放缓差异较小，此时主要受较小温差影响.

不同长度下载体入口处温度梯度变化如图11所示.由图11可知，随载体长度增加，(dT/dx)1-2极值降低且下降速率逐渐减少，温度梯度的持续时间变化较小.这一结果与孟忠伟等[17]研究结果相一致，根据研究显示，增加载体长度有利于吸收温度能量，使得载体内部能量传递区域缓慢，降低温度梯度.这是因为载体长度增加，体积和过滤面积相应增大，总质量增加.载体前端在遭受热冲击时可将热量分散在更大的接触面积，降低与后续载体之间的温差，降低温度梯度.但增加载体长度与4.1节所述增加排气流量相同，都无法改变载体先前端升温再后端升温的顺序，无法达到载体各处同时升温，因此(dT/dx)max的下降速率逐渐减少.当载体长度较长时，更低的传热速率避免较大的温度梯度，同时也导致后续载体因长度增加而延长温度梯度持续时间；当载体长度较短时，虽然遭受热冲击时温度梯度急剧上升，但后续载体传热速度快，升温速率高，缩短了温度梯度的持续时间，因此载体长度对温度梯度持续时间影响较小.通过研究载体长度对DPF温度特性的影响可知，DPF的长度对温度特性影响很大，因此在实际运用中，应当在空间布局合理的情况下选择合适的DPF长度，从而减少载体的升温速率，对减缓DPF入口热冲击破坏，延长使用寿命有很大作用，但增大的迟滞时间不利于控制策略的快速响应和反馈调节.

图11 不同长度下温度梯度随时间变化

3.4 颗粒物负载量对DPF载体温度影响

不同颗粒物沉积量下载体温度和升温速率变化如图12所示.

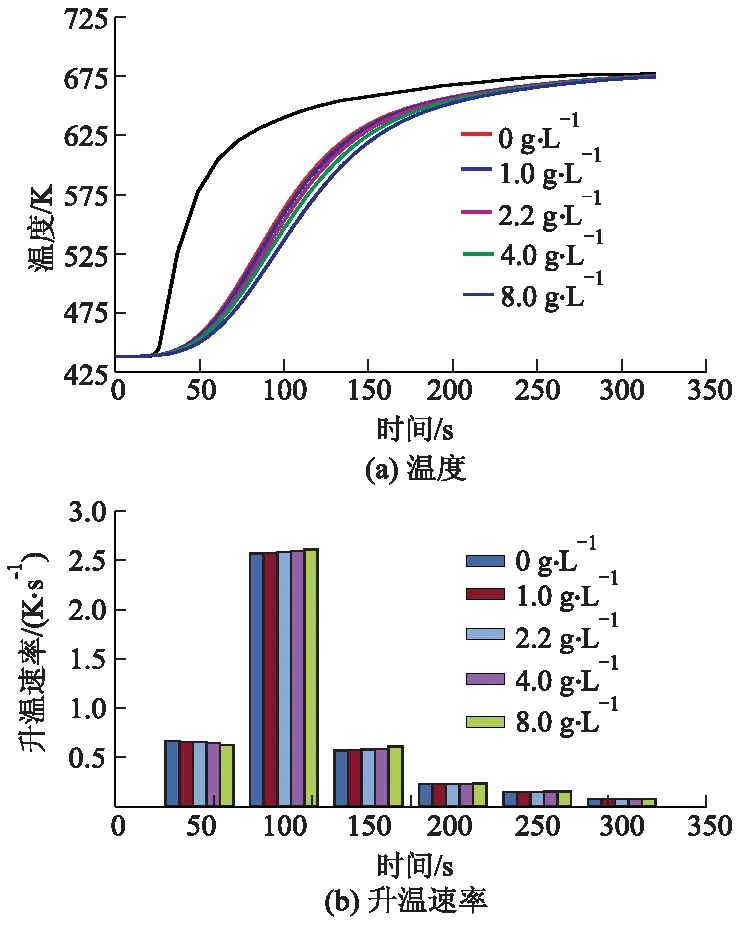
图12 不同沉积量下温度及升温速率随时间变化

由图12a可知，当颗粒物沉积量分别为0、1.0、2.2、4.0和8.0 g·L-1时，tmax分别为42、44、47、51和56 s，整体的迟滞时间呈增加状态，从右侧放大图上可以更加清晰地看出增加趋势，说明颗粒物沉积量与前后端迟滞时间具有正相关性.由图12b可知，在升温初始时刻，随负载量增加升温速率减少；在100 s至200 s范围内升温速率随负载量增加而增加；在200 s后，各负载量下载体升温速率近似相等.这是由于当负载量增加时，载体壁面碳烟层厚度增加且孔道尺寸发生变化，DPF壁面可通过性降低，壁面过滤速度总体降低，气流流动受阻，对流传热减弱，最终导致迟滞时间增加.这个结论与S.BENSAID等[18]的研究较为一致.根据S.BENSAID等[18]以及M.A. MOKHRI等[19]的研究显示，当DPF内部碳载量增加时，DPF入口端和出口端的气体渗流速度逐渐下降，中部区域的气体渗流速度逐渐上升，沿DPF轴向渗流速度分布将变得更加平坦，但总体速度下降.由于模型中假设颗粒物在孔道中均匀平铺，整体厚度较小，对气体流动的阻碍作用有限，导致各负载量迟滞时间差异较小.

不同负载量下载体入口处温度梯度变化如图13所示.由图可知，当颗粒物沉积量为0、1.0、2.2、4.0和8.0 g·L-1时，(dT/dx)1-2极值分别为1 465.88、1 478.62、1 493.24、1 521.16和1 621.21 K·m-1，呈指数型上升趋势，且温度梯度持续时间小幅上升.原因是颗粒物沉积量增加降低DPF壁面渗透率，延长了气体在载体内部的滞留时间，同时降低传热速率，使热量在载体内部出现积聚，引起温度梯度上升.当颗粒物沉积达到极限，即孔道完全堵塞时，热量将被限制在孔道内无法向后续载体传递，温度积聚在此时达到最强，温度梯度在短时间内会大幅度上升接近甚至超过载体可承受最大温度梯度限值，因此(dT/dx)1-2极值随着颗粒物沉积量的增加上升速率不断增加.因而颗粒物沉积量对DPF温度特性有很大影响，颗粒物的累积会明显提高温度梯度极值，增强内部温度积聚作用，造成DPF热应力破坏隐患.在实际应用中，当DPF局部区域负载量较大时，会引起对应区域的温度梯度增加，但对整体的压降没有太大影响，如果继续负载直到压降到达限值时进行再生操作，颗粒物阻塞的区域会在再生过程中产生陡峭的温度梯度，在整体压降满足再生条件下造成热应力破坏.因此，可根据模拟的试验结果反向推断出DPF的局部颗粒物沉积程度，进而制定更加准确的再生策略.

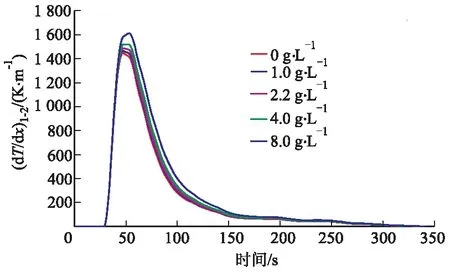
图13 不同沉积量下温度梯度随时间变化

4 结 论

1) 提高来流流量，迟滞时间tmax和轴向温度梯度极值下降且下降速率减少.增加入口流量能够增强对流传热，大幅加速DPF的升温过程，减小载体前后端升温的迟滞时间和内部的温度梯度，但增加流量只能减缓DPF受到的热冲击，无法消除热冲击引起的温度梯度和迟滞时间.

2) 增加载体孔目数，迟滞时间tmax和轴向温度梯度极值均线性降低.增加DPF载体孔目数有助于加速载体升温，促进温度分布均匀，线性降低DPF前后端升温迟滞时间和温度梯度，对减小DPF再生频率，延长DPF使用寿命有很大作用.

3) 增加载体长度，迟滞时间tmax线性增加，轴向温度梯度极值降低且速率减少.DPF长度对DPF温度特性影响较大，增加DPF长度有利于减小载体升温速率，降低内部的温度梯度，减缓DPF入口热冲击破坏；但较小的升温速率延长了迟滞时间，不利于使用过程中控制策略的快速响应和反馈调节.

4) 增加颗粒物沉积载量，迟滞时间tmax上升，轴向温度梯度极值呈指数上升.颗粒物沉积对DPF温度特性有很大影响，颗粒物负载量增加对迟滞时间的影响较小，但会导致温度梯度快速上升，增加DPF使用过程中热损坏的风险；通过温度特性可反应DPF局部区域的负载情况，进而反向推断出DPF内部颗粒物的沉积量，确定更加准确的再生时刻.