基于小生境聚类的改进MOEA-D 算法*
2021-01-24汤恺祥
汤恺祥,许 峰
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
2006年,Deb[1]和 Brockhoff[2]指出,现实中的许多优化问题是多目标优化问题(Multi-objective Optimization Problem,MOP),而其中的高维多目标优化问题(Many-dimensional Multi-objective Optimization Problem,MaOP)的比重越来越高。多目标进化算法(Multi-objective Evolutionary Algorithm,MOEA)在如今的研究领域中是公认处理MOP 的有效优化方法,但MOEA 在处理MaOP 时就显得能力不足,其表现在处理问题时性能的低下,对真实的Pareto 前沿表示不准确,结果分布性不均匀和稳定性不理想等问题。
目前有两大类可以较好的处理MaOP 的MOEA。一类是基于精英选择的多目标进化算法,另一类是基于多目标分解的多目标进化算法。
2007年,Zhang[3]提出了一种基于分解的演化多目标进化算法;2010年,GU[4]提出一种新的权重向量设计机制;2014年,Qi[5]提出了一种基于分解的动态调节权重向量的多目标进化算法(MOEA-D-AWA);2016年,Blasco[6]在进行高维Pareto 前沿分析时引入了相似距离;2017年,Bi[7]在一种多目标进化算法中引入了小生境方法;2018年,Monalisa[8]在一种多目标进化算法中引入了聚类思想。
在MOEA-D-AWA 中并没有考虑优化种群替换方法,本文提出在MOEA-D-AWA 基础上引入小生境与聚类思想来优化种群替换,以达改进算法分布性的目的。利用标准测评函数对改进算法进行了性能测试,并与相关算法进行了比较。
1 MOEA-D 算法
MOEA-D 算法主要用于解决MaOP,其思路是将多目标优化问题分解成若干个单目标子问题,然后利用多目标进化算法处理这些若干个子问题。其主要概念及步骤如下[3]:
1.1 权重向量的生成
MOEA-D 使用单格子算法生成较均匀的权重向量,且满足以下条件:

1.2 构建聚合函数的TCH 分解方法
TCH 方法(Tchebycheff):权重向量 λi中子问题表示为:

1.3 邻域的选取与作用
在MOEA-D 中,计算权重向量间的欧式距离获取子问题的邻域。算法利用邻域定义,获取父代解,繁殖子代解,且保证解的多样性。
MOEA-D 基本步骤如下:
步骤1 初始化。得到初始种群P,权重向量λ,各个权重向量邻域内T 个向量等。
步骤2 更新操作,随机选取第i 个体,在第i 个体的邻域中随机选取两个个体进行交叉变异操作,获得新个体y。更新z*即参考点和邻域中的解:判断新个体的适应度是否优于第i 个体邻域中个体的适应度,优于则替代邻域个体,劣于则不更新。
步骤3 终止,满足条件则输出非支配解集;否则转到步骤2。
2 MOEA-D-AWA 算法
MOEA-D 的结构模块主要有:(1)优化问题分解;(2)演化算子;(3)子代更新;(4)权重向量,许多改进研究就以这些模块为基础进行。从文献[9]中的大量数值实验显示,MOEA-D 在求解大规模高维多目标优化问题时性能欠佳。因此,Qi[5]与Ma 提出了基于分解的动态调节权重向量的多目标进化算法(MOEA-D-AWA)用于改进以上问题。
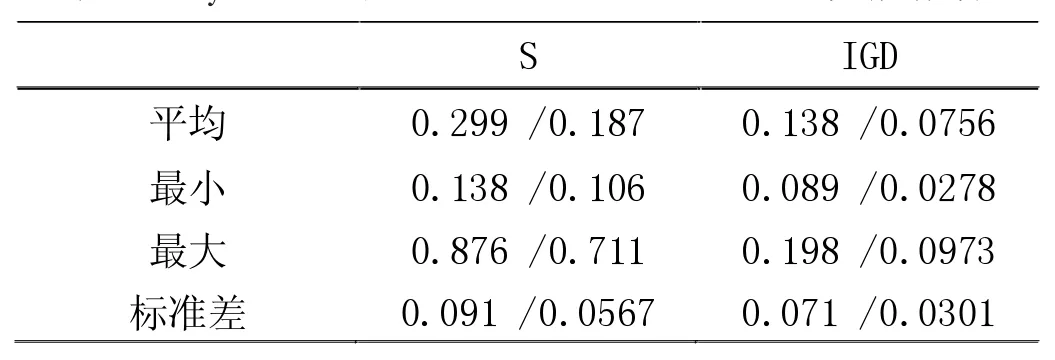
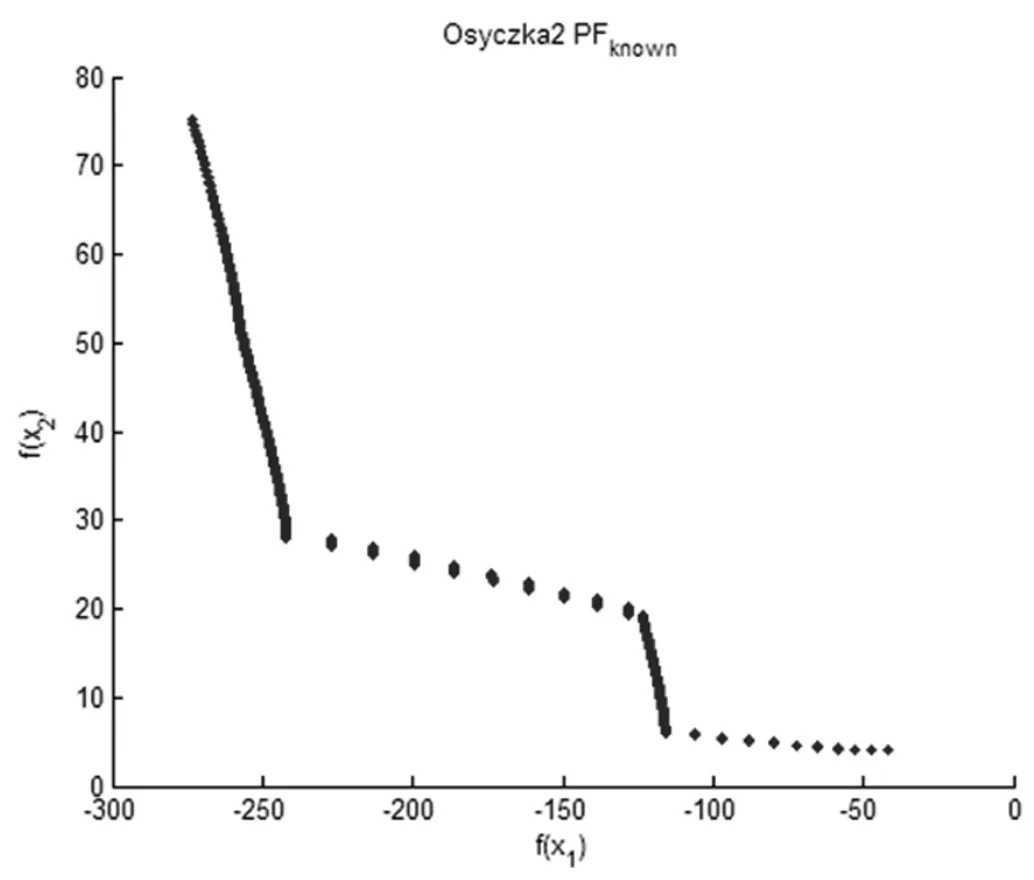
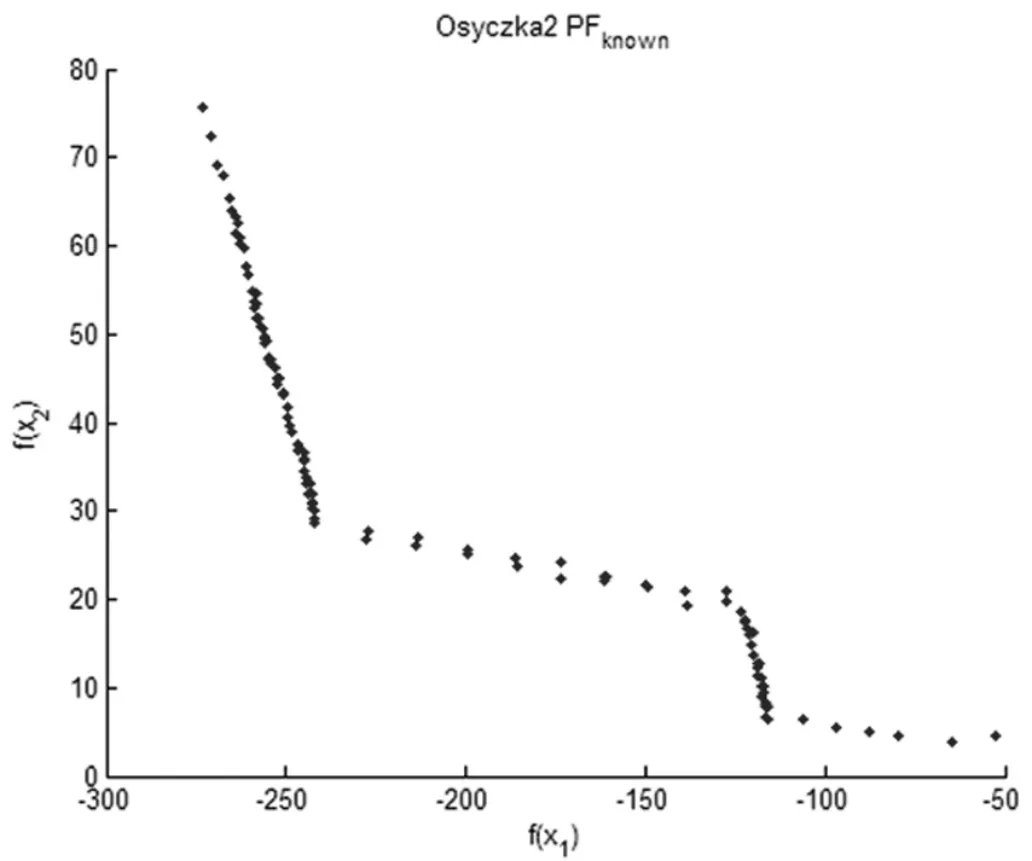
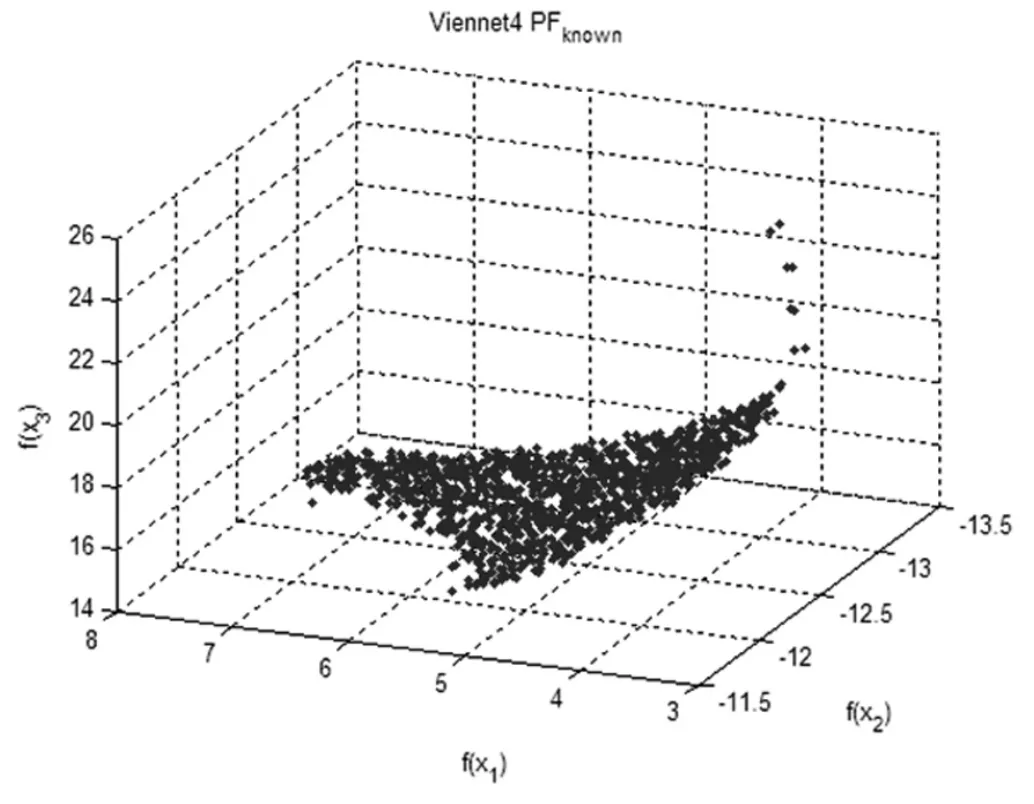
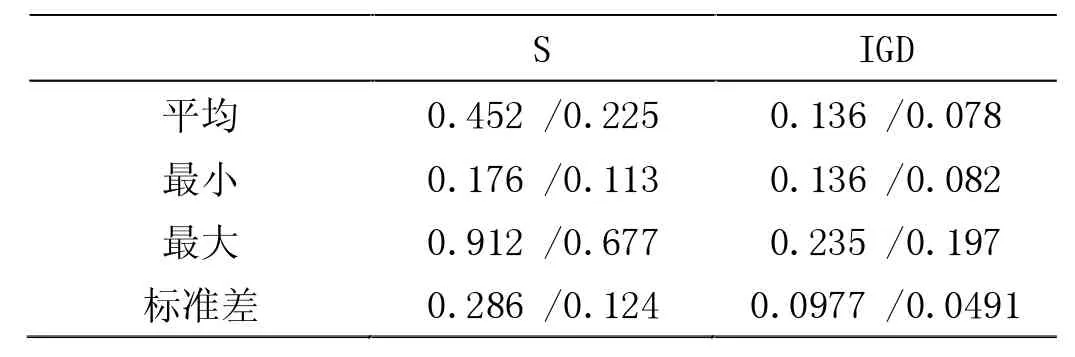
动态调节权重向量在MOEA-D 框架的基础上进行改进的,其基本原理并不复杂。基本思路为:利用目前解集和一个非支配解集动态调节权重向量。主要过程为:已知当前种群P 及种群大小为N,计算P 中每个个体的拥挤度,拥挤度计算方法见文献[5]。当种群P 中有过于拥挤的群(超出自定义数值)时,删除拥挤度最高的一个个体解并重新计算P 中每个个体的拥挤度。如果种群P 动态调节的权重向量生成公式如下: 动态调节权重向量的方法可以对MOEA-D 算法获得的解起到提高分布性和保持种群多样性的作用。 文献[5]中研究了MOEA-D-AWA 算法对MOEA-D算法的改进效果,并将其改进的算法与其他相关的多目标进化算法的结果进行了比较。 从权重向量选择的方向分析,该算法的优点是动态调节权重向量的方法可以在PF 复杂(如不连续的PF 或具有尖峰的PF)的情况下,很大程度上保证权重向量的均匀性和确保解集均匀分布在PF 上。但是从种群替换的方向分析,该算法中,交叉变异产生一个好子代可以取代大部分差的子代,这就导致种群多样性变差,即种群替换方向存在缺陷。因此,在利用该算法时,合理的方式是动态调节权重向量和优化种群替换这两种策略合理互补。在满足原优点的同时,尽可能确保种群多样性和解的分布性。 在文献[5]的基础上,本文提出一种基于小生境中聚类的改进MOEA-D-AWA 算法,具体如下: 定义清除算法(小生境)相关距离: 个体 i=(x1,x2,...,xn)与个体 j=(y1,y2,...,yn)的距离公式为: 小生境中心点为 X1,X2,...,Xm其余个体为 Y1,Y2,...YM,D(Xm,YM)表示中心点与个体间的相关距离。相关距离越大,个体与中心点越近。 DBSCAN 聚类密度算法[11]中的相关定义: 参数:(1)epsilon 表示点的邻域半径;(2)minPts 邻域内至少包含个体的数量。 根据参数,样本中的个体将分成三类: (1)NBHD(p,epsilon)>=minPts 为核点;(2)NBHD(p,epsilon) 基于小生境聚类的改进MOEA-D(NC-MOEA-D)步骤如下: 步骤1 初始化。得到初始种群P,权重向量λ,各个权重向量的邻域内T 个向量等。 步骤2 更新操作。 (1)对父代种群Pt,根据MOEA-D-AWA 交叉变异方式得到U。 (2)对U 采取清除算法(小生境)操作,即首先对U中个体根据适应度值进行降序排列,将第一个个体作为第一个小生境中心。其次利用上述相关距离方法判断当前个体到所有小生境中心的最短距离是否大于自定义数值,是则形成新的小生境,不是则加入最近的小生境中。最后小生境生成完毕,多出的个体降低其适应值。 (3)将生成的每个小生境进行DBSCAN 聚类操作,即首先在小生境中任选一个点,计算其NBHD(p,epsilon)值并判断是否为核点。是则建立类,不是则成为外围点。其次,处理其余点直到将density-reachable 点也加入类中(当外围点加入类中时状态改为边缘点)。最后重复上述操作直到遍历完所有点。 (4)在每个小生境中只保留聚类中心(即核点)和外围点,得到子代种群Qt。 (5)将Pt和Qt合并且根据聚合函数更新父代种群Pt+1。 步骤3 若满足终止条件,则输出最终的解,否则重复步骤2。 MOEA 性能评测指标分为四种[10],具体为容量指标、收敛性指标、多样性指标、收敛性和多样性综合指标。根据本文新算法的优化点为分布性的改进,考虑采用分布性指标(S)与综合指标(IGD)。定义如下: 其中P*表示理想PF,P 表示算法求得的近似PF,d(v,P)表示个体v 到P 中个体的最小欧几里德距离。IGD指标越小,算法分布性越好。 下面用基于小生境聚类的MOEA-D 算法对Osyczka2 和Viennet4 两个标准测试函数进行优化仿真,并将结果与经典的MOEA-D 算法的结果进行比较,从而检验改进算法的性能。 图1、图2 和图3、图4 分别给出了用 NC-MOEA-D和 MOEA-D 得到的 Osyczka2 和 Viennet4 的 Pareto 最优前沿。 表1 和表2 分别给出了用NC-MOEA-D 和MOEAD 得到的Osyczka2 和Viennet4 的性能评测指标。 表1 Osyczka2 的MOEA-D/NC-MOEA-D 性能指标 图1 Osyczka2 的 Pareto 最优前沿(NC-MOEA-D) 图2 Osyczka2 的 Pareto 最优前沿(MOEA-D) 图3 Viennet4 的 Pareto 最优前沿(NC-MOEA-D) 图4 Viennet4 的 Pareto 最优前沿(MOEA-D) 表2 Viennet4 的MOEA-D/NC-MOEA-D 性能指标 从图1~图4 及表1 和表2 可以清楚地看出,基于小生境聚类的MOEA-D 算法与常规MOEA-D 算法相比,在分布性和均匀性指标上有了一定程度的改善,能够有效地处理复杂的多目标优化问题。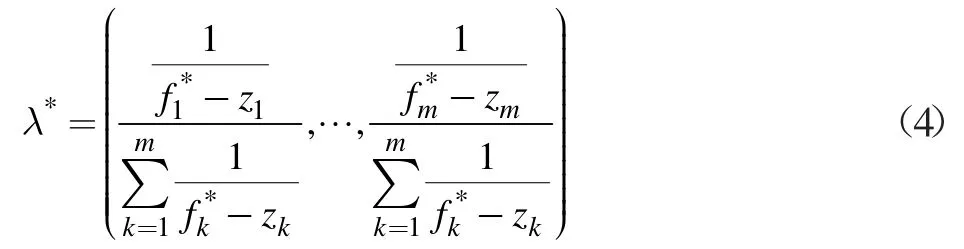
3 基于小生境聚类的改进MOEA-D-AWA

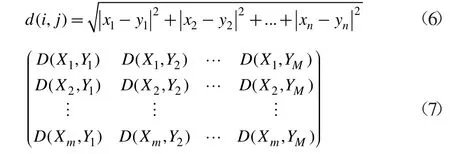
4 数值实验与算法性能评测
4.1 算法性能评测指标
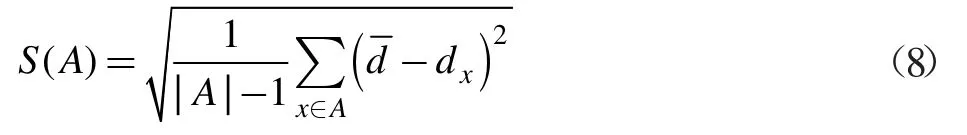
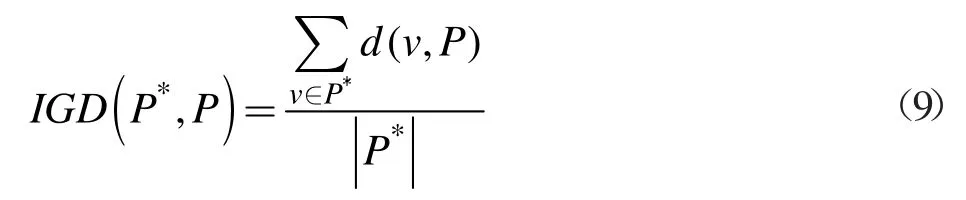
4.2 数值实验结果