基于协同进化策略改进的MOEA/D 算法*
2021-01-24王启翔
王启翔,许 峰
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
2007年,Zhang[1]提出了基于多目标分解的MOEA/D,但是随着目标维数的上升,全局搜索能力下降,容易陷入局部最优。为了改善MOEA/D 算法,许多学者做了大量研究、改进工作。2018年,Ryoji[2]分析了MOEA/D 的控制参数;2020年,Dong[3]提出了自适应权重 MOEA/D;Zhang[4]提出了基于信息反馈的MOEA/D;Wang[5]提出了自适应演化策略MOEA/D;Zhang[6]提出了多阶段动态演化MOEA/D;Fan[7]提出了基于角度约束的MOEA/D。
2009年,张敏[8]提出了一种基于正态分布交叉的MOEA算法;2019年,Zhang[9]将差分算子引入 MOEA 算法,提出了一种双变量控制MOEA/D 算法。本文在上述工作的基础上,将正态分布交叉算子和差分进化算子引入MOEA/D,构成协同进化,并用标准多目标优化测验函数对改进算法进行了性能测试,验证了新算法的有效性。
1 MOEA/D 算法
MOEA/D 通过预先设定的权重向量将复杂的多目标优化问题转变为一系列的单目标问题,每一个子问题使用与其相邻的子问题提供的参考信息,相互协同进化,主要用于求解MaOP。该算法采用Tchebycheff 分解法,MOEA/D 的基本步骤如下:
(1)N:子问题的个数;
(2)N 个均匀分布的权重向量:λ1,λ2,...,λN;
(3)T:每个权重向量邻居的个数。
步骤1 初始化:
(1)设EP=Φ。
(2)计算任意两个权重向量之间的欧几里德距离,为每个权重向量选出最近的T 个权向量作为它的邻域。即 λi1,λi2,...,λiT是离 λi最近的 T 个权重向量,i=1,2,…,N,令 B(i)={i1,i2,…,iT}。
(3) 根据权重向量来产生初始种群 x1,x2,…,xN。
步骤2 更新:
对 i=1,2,…,N:
(1)从 B(i)中随机选取两个序号 k,l,对 xk和 xl执行SBX 算子产生一个新的解y。
(4)更新EP:剔除EP 中受y 支配所有的向量,并且在EP 中向量都不支配y 时,令EP=EP∪{f(y)}。
步骤3 终止条件:如果满足终止条件,则停止并输出EP,否则转步骤2。
2 交叉算子
交叉算子是进化算法领域中最为关键的存在,交叉算子的优劣往往能够决定算法的优劣。最经常用的交叉算子就是Deb 提出的模拟二进制交叉算子,其定义为:对两个父代个体 X1和 X2,如下操作得到子代个体
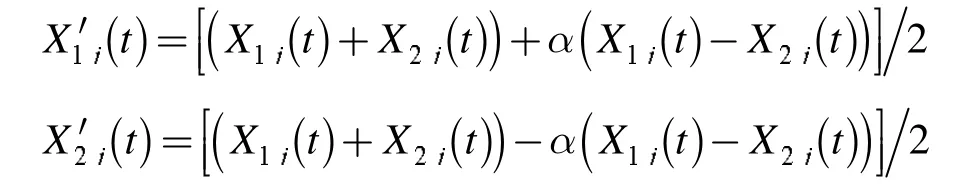
其中,j=1,2,…,n,α 是随机变量,每一维上都要重新产生,方式如下:
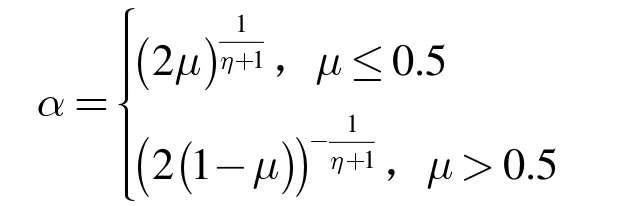
μ 是分布在(0,1)上的随机数;η 是交叉参数。
正态分布交叉算子(NDX)是张敏[8]等在2009年提出的,就是将正态分布引入SBX 算子中,其定义为:对两个父代个体 X1和 X2,如下操作得到子代个体
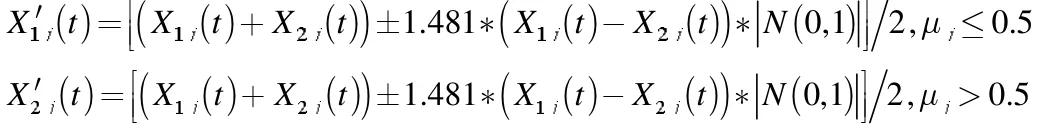
其中,μj是(0,1)区间上的随机数。
在设计NDX 的时候,引入重组操作,增强了NDX 算子空间搜索能力。NDX 相较SBX 的优势在于对大量的个体进行重组操作,能够扩大种群的多样性,提供更大的搜索范围。
DE/best/2 引入了最优解个体引导搜索方向,变异个体的生成受到最优解个体的制约,搜索范围将围绕最优解展开,因而使得算法的收敛速度大大增加,趋向最优解的能力提高,然而若当前最优解个体为局部极值点,则会因为种群多样性降低而增大陷入局部最优解的可能性。
3 协同进化策略
在多目标进化算法中,如果一个算法能有一个优秀的产生子种群的策略,那么这个算法的性能必定会大大提高。MOEA/D 利用模拟二进制交叉算子SBX 来生成子代,并且取得比较好的效果,但是该算法的搜索能力较弱,生成的种群多样性较差,且SBX 算子易产生劣质子代等等。针对这些缺陷,本文利用NDX 正态分布交叉算子和DE/best/2 差分进化算子来构建协同进化策略,替换SBX 算子,让NDX 算子和DE/best/2 算子共同生成子代。
首先NDX 可以对子问题邻域内大量的个体进行重组操作,使父代个体更具多样性,从而能够产生多样性的个体,扩大种群多样性,提供更大的搜索范围;其次,从NDX 产生的种群中,执行DE/best/2。
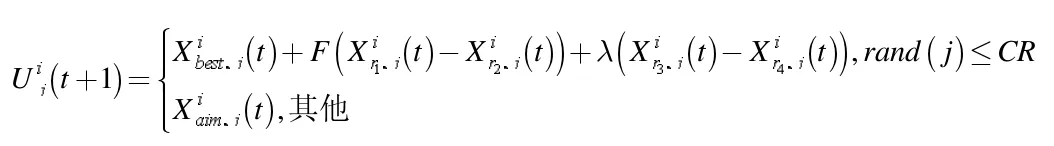
4 协同进化策略改进的MOEA/D 算法
步骤1 初始化参数。生成一组分布均匀的权向量λ1,λ2,……,λN,计算子问题邻域 B(i)={i1,i2,…,iT},根据权向量生成一个初始随机种群 P={x1,x2,…,xN},取每一个目标值的最小值作为参考点
步骤2 种群更新。
对 i=1,2,…,N
(1) 对 B(i)中所有个体,两两执行 NDX 算子,得到新的子代种群记为Q(i)。
(2) 将 B(i)和 Q(i)合并,记为 Rt。
(3)从Rt选择合适的个体,执行DE/best/2 算子,生成新个体y。
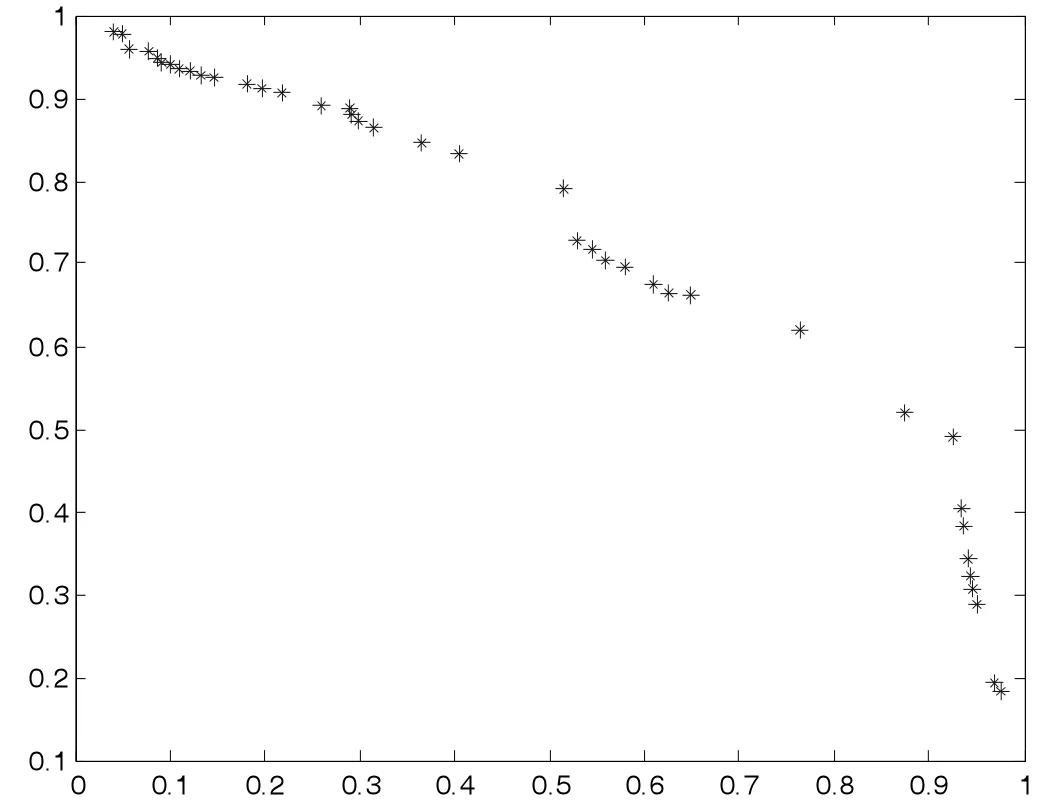
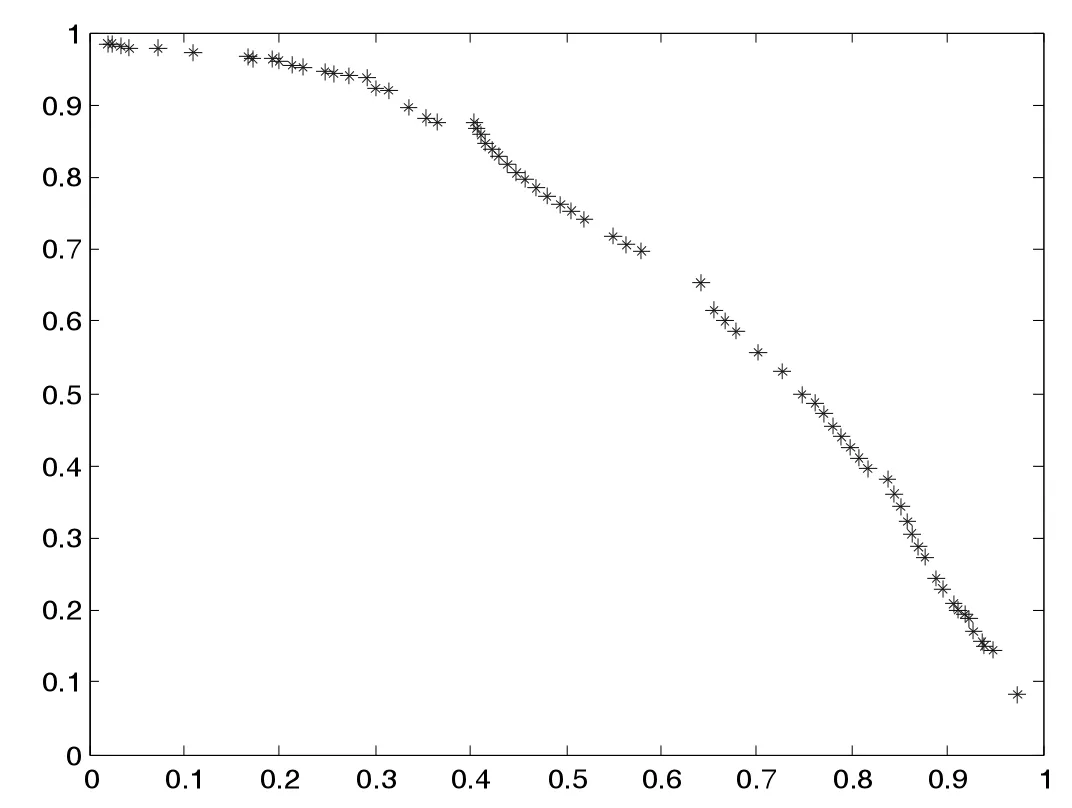
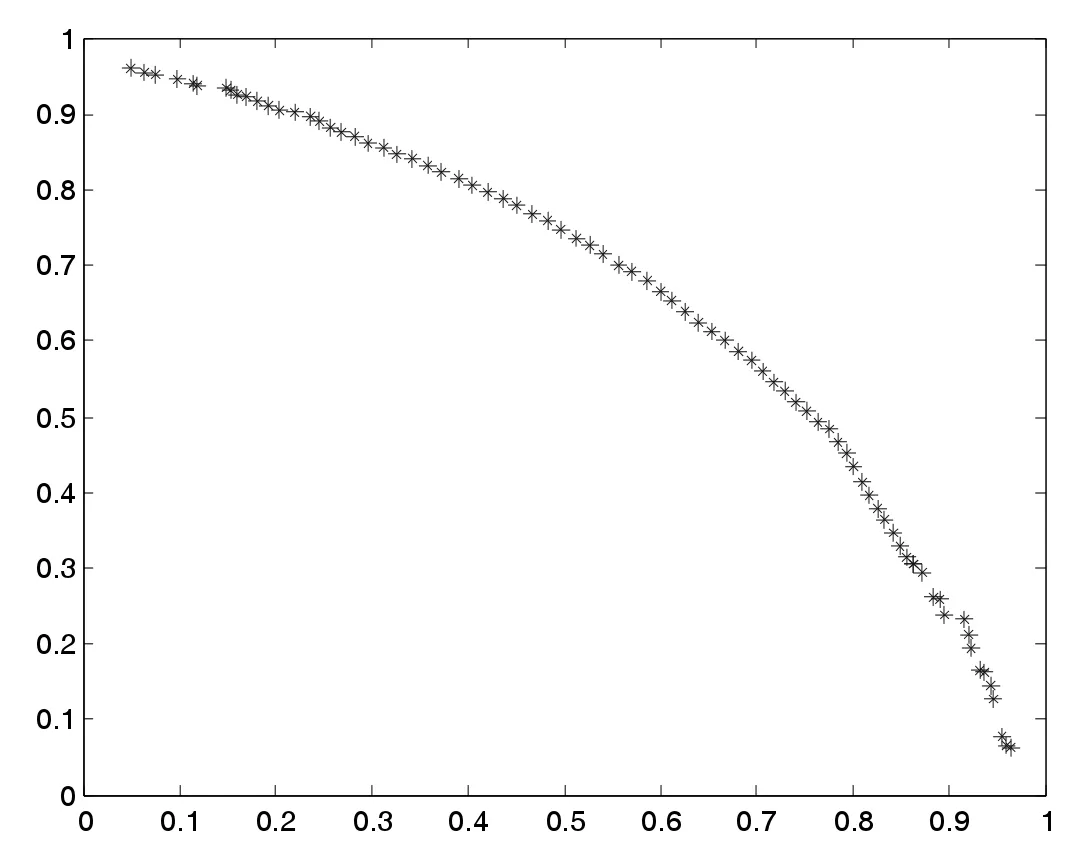
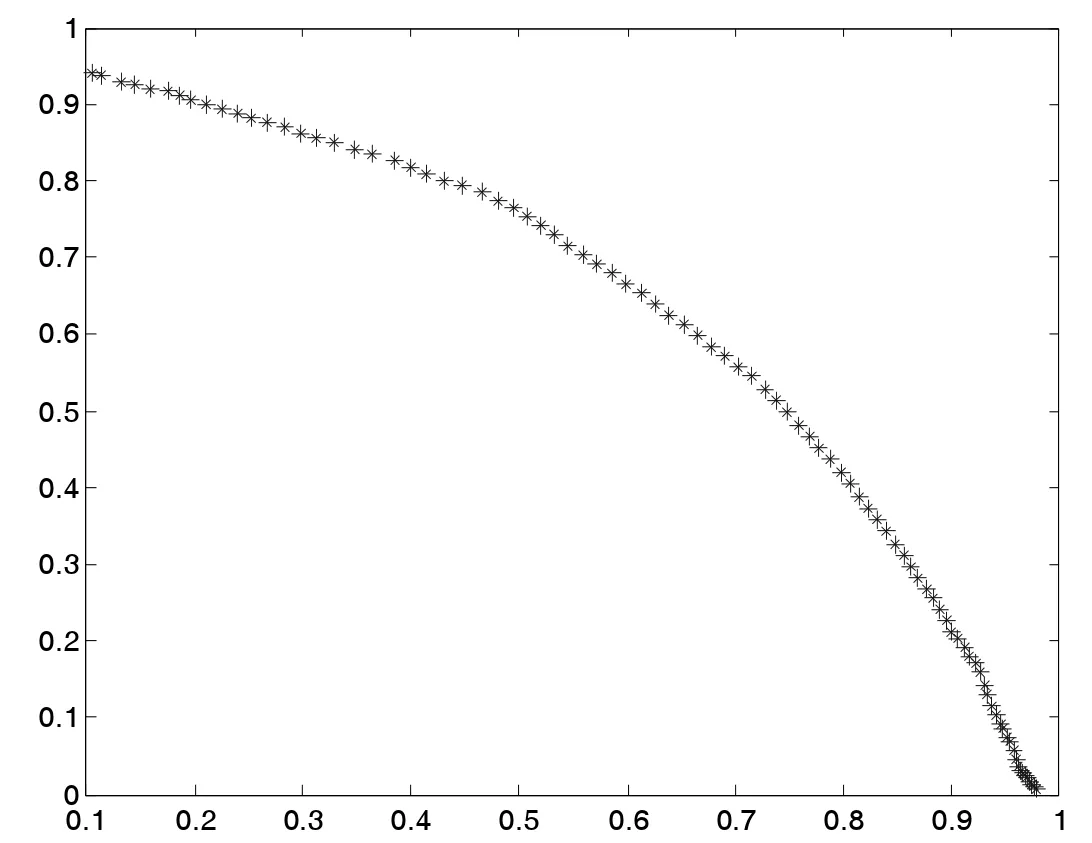
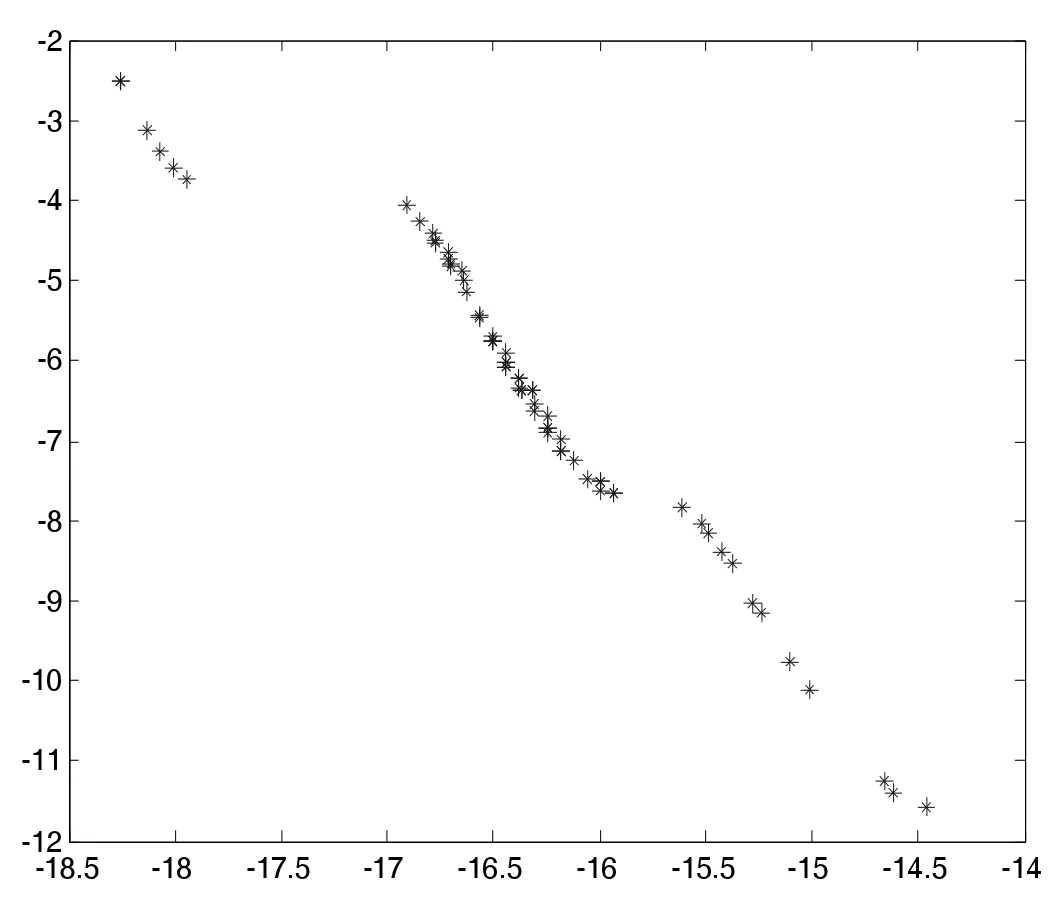
(4)若zj 步骤3 更新EP。如果新生成的解y 不被EP 中的任何解所支配,并删除由y 主导的解。 步骤4 终止条件:如果满足终止条件,则停止并输出EP。否则转到步骤2。 为了评测改进算法的收敛性和分布性,选取下面两个标准测试函数进行数值计算: 其中,-4≤x1,x2,x3≤4。 其中,-5≤x1,x2,x3≤5。 首先进行非支配解个数的生成比例实验,这是评测算法收敛性的一种直观方法。下面给出了非支配解不同生成比例时F1的Pareto 最优前沿。 图1 40%非支配个体 图2 60%非支配个体 上述图1-图4 图形显示,对于固定的种群规模,随着非支配解比例的增加,算法较好地逼近了理论上的Pareto 最优前沿。这在一定程度上表明,改进算法具有较好的收敛性。 下面再将改进算法与标准MOEA/D 算法进行比较。下面给出两种算法的对比Pareto 最优前沿。 从上述图5-图6 图形可以清楚地看出,改进的MOEA/D 与标准的MOEA/D 相比,有较好的分布性和均匀性。 图3 80%非支配个体 图4 90%非支配个体 图5 F2MOEA/D 的Pateto 最优前沿 图6 F2 改进MOEA/D 的Pateto 最优前沿 受以往工作的启发,本文将正态分布交叉算子和差分进化算子引入MOEA/D,数值实验表明,改进后的算法维持了MOEA/D 的良好收敛性,而且较MOEA/D 在分布性和均匀性方面有了一定程度的改进。不过,这不可避免地增加了算法的复杂度。5 数值实验与性能测试
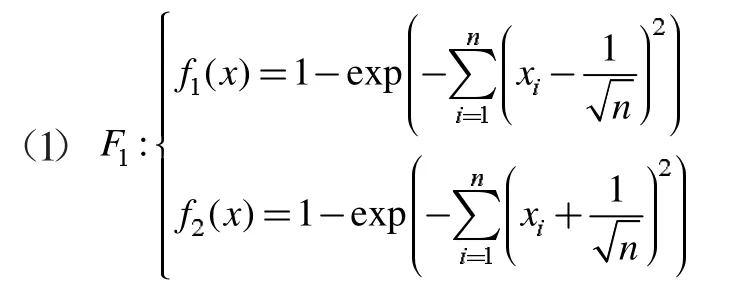
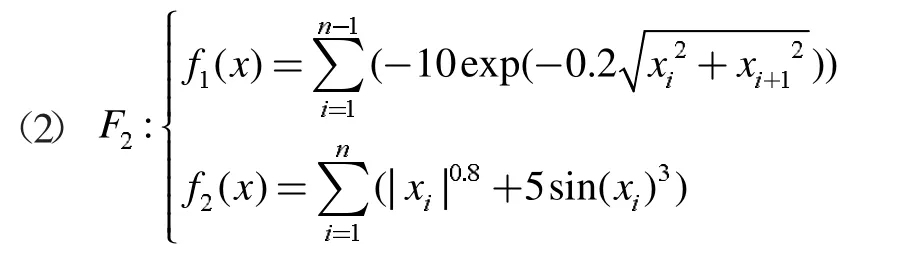
6 结论

