轴缺陷检测中的快速均值滤波应用研究
2021-01-23姜庆胜李研彪计时鸣
姜庆胜,李研彪,计时鸣
(浙江工业大学 机械工程学院,浙江 杭州 310023)
轴是机械行业普遍使用的零部件,其表面缺陷对使用性能和寿命有重要影响。利用机器视觉自动检测轴表面缺陷,可有效提高检测效率、检测质量、保护检测人员健康,笔者采用线扫描方法获取表面的图像。根据缺陷尺度识别要求,采集图像的分辨率为16 384×4 096,达到6 700万像素。针对6 700万像素的高分辨率图像(相对于大多数工业应用采用2 000万以下像素成像而言),图像处理算法的耗时,直接影响机器视觉自动检测系统的工作效率,因此选择合理的图像处理算法,改善图像处理计算效率,具有重要的意义,其中图像滤波的算法是比较耗时的算法之一。图像滤噪算法包括均值滤波法、中值滤波法、高斯去噪和小波变换等。均值滤波[1]因为其计算简单,能滤除卷积模板面积以下的斑点,相对其他方法速度更快,是一种实用的方法,但在实际应用中,如何减少算法的计算量,提高算法的计算效率是一个瓶颈问题。Rakshit等[2]、Pan等[3]和Nakariyakul[4]提出通过减少重复计算的方法来加快均值滤波计算速度;王科俊等[5]、夏永泉等[6]和何石等[7]等研究了通过减少重复计算的方法来达到加速目的的算法;张成斌等[8]采用对非噪声点不做滤波处理的方法来减少均值滤波的计算次数;何海明等[9]提出求通过检索怀疑为噪声点像素的均值的方法来加速计算;王博[10]针对超声图像滤除噪声斑点,提出直接在卷积模板内选取8个点作为样本参与均值计算,而不受模板大小影响。以上这些方法,其本质都是通过减少计算次数的方式来加快运算速度。
笔者针对所研究的活塞轴表面图像具有背景单一、图像矩阵噪声污染点稀疏的特点,对比分析若干图像滤噪算法的运算效率,探索减少计算耗时的基本方法,并在基于均值滤波海量数据去冗余的方法[11]和卷积神经网络Atrous训练提速方法[12]的基础上,提出了一种基于去除冗余数据的Atrous均值滤波算法的镂空滤波算法,以满足研究中涉及汽车减振器活塞轴表面机器视觉自动检测系统的应用需求。
1 轴表面缺陷检测系统
笔者研究的对象是轴的表面缺陷,如图1所示,轴长为200~400 mm,直径为20 mm,检测的缺陷目标最小直径0.3 mm的凹坑,所以拟采用6 700 万像素的线扫描相机来采集图片。

图1 轴及其表面缺陷
根据检测对象,轴表面缺陷检测系统如图2所示,虚线框内就是笔者研究的目标。

图2 缺陷检测和分类系统
图像预处理是整个检测系统的重要环节,处理方法越简单,速度越快,所以采纳均值滤波是合适的选择。
2 传统均值滤波
对于均值滤波的图像处理[13],其计算表达式为
(1)
式中:A为被处理图像f(i,j)上点(i,j)的一个邻域;M为邻域A中像素点的个数,也称为面积。用计算结果F(i,j)来取代(i,j)位置的原像素值,这是一种空间域局部处理算法。
均值滤波也叫线性平滑滤波,其一般式是具有权值的表达方式,也具有卷积特性提取效果,可有效提取重要特征,滤除噪声。假设一幅M×N的图像经过一个大小为m×n(m和n为奇数)的卷积的一般式为
(2)
式中:w为权值;分母为卷积核的系数之和。传统均值滤波可以滤除卷积核面积以下的噪声污染斑块。
3 几种改进的快速均值滤波方法
3.1 改变数据相加方法
传统均值滤波大部分计算是数据的相加,所以研究的重点在加法的方法上[14-15]。计算机语言进行数据相加的方法很多,不同的相加方式,其运算时间却相差很多。如算法1是常见的计算方法,如果将其改为算法2,速度就会明显提高。
算法1数据累加
temp+=p(i1,j1)
temp+=p(i1,j2)
…
temp+=p(i1,jn)
temp+=p(i2,j1)
…
temp+=p(im,jn)
pix=temp/(mn)
算法2数据直接相加
pix=(p(i1,j1)+p(i1,j2)+…+p(im,jn))/(mn)
3.2 改变数据读取方式
CPU高速缓存是用来加速处理器访问内存的部件。在金字塔式存储体系中它位于自顶向下的第二层,仅次于CPU寄存器。其容量远小于内存,但速度却可以接近处理器的频率。当处理器发出内存访问请求时,会先查看缓存内是否有请求数据。如果存在,则不经访问内存直接返回该数据;如果不存在,则要先把内存中的相应数据载入缓存,再将其返回处理器。
缓存从内存中读取数据一般都是整个数据块,所以它的物理内存是连续的,而二维数组数据的存储都是按行在物理内存中连续存储,如果内循环以列的方式进行遍历的话,将会使整个缓存块无法被利用,而不得不每读取一个数据,缓存就要从内存中读取数据,而从内存读取数据的速度是远远小于从缓存中读取数据的,这样就大大延长了滤波运算时间。所以数据的读取方式应按行来读取数据,算法4即是对算法3的改进。
算法3按列读取数据
p(m,n)
For(intj=k;j formula 1 For(inti=k;i formula 2 }} 算法4按行读取数据 p(m,n) For(intj=k;j formula 1 For(inti=k;i formula 2 }} 在均值滤波中求解每个像素值的加法计算,必然存在着很多重复的像素加法计算。比如第一个像素的某些像素的和,在第二个像素计算中可以直接利用,通过这样编程来减少加法的次数,从而实现加速的目的,计算表达式为 (3) 式中:A′为某一领域A范围的某行或某列;P为该列或行的和;F为最后所要得到的像素值;M为A领域内参与计算的像素个数总和。实现方式描述见算法5。 算法5减少重复加的算法 For(j=0;j P1=p(i1,j1)+p(i1,j2)+…+p(i1,jn) P2=p(i2,j1)+p(i2,j2)+…+p(i2,jn) P3=p(i3,j1)+p(i3,j2)+…+p(i3,jn) P4=p(i4,j1)+p(i4,j2)+…+p(i4,jn) For(i=0;i P5=p(i,j1)+p(i,j2)+…+p(i,jn) pix=(P1+…+Pn)/(mn) P1=P2;P2=P3;P3=P4;P4=P5;… }} 该项目的研究对象是如图1所示轴的表面缺陷,通过线扫描相机采集线扫描图像,这种线扫描图像如图3所示,特点是背景单一。 图3 轴表面缺陷典型线扫描图像 由图3可知:扫描图像矩阵为噪声污染稀疏型矩阵,所以必然有很多的数据其实是冗余的,没有必要参与滤波计算。通过去除冗余数据来减少计算次数,笔者提出了一种达到加快运算速度的滤波方法,称为Atrous滤波法,其属于一种加权均值滤波算法。Atrous滤波法采用Hadamard积来去除冗余数据,Hadamard公式为 (A·G)xy=axygxy (4) 式中:A为被滤波图像的矩阵;G为仅含“1”和“0”元素的矩阵;axygxy为经过去除冗余数据的滤波对象。其中矩阵G中“1”和“0”的选择原则依据引入的“rate”概念来确定,当rate=0的时候,矩阵G的所有元素都是“1”;当rate=1时,每间隔一个“1”之间是“0”元素;以此类推,当rate=2时,每个“1”之间有2个“0”。同样引入“gap”概念,即gap=1时,每隔一行和列为1个“0”元素,以此类推,gap=2时,每隔两行和列为2个“0”元素。Atrous滤波公式为 (5) 根据Atrous滤波法,以卷积核7×7和9×9为例,分别选取不同gap值时,不同分辨率图像滤波速度的比较如图4所示,其中采用的图像分辨率如表1所示。 图4 不同分辨率图像下的运行时间 表1 不同分辨率图像 由以上提出的方法可知:减少冗余数据可以明显加快速度,而且随着图像像素的提高,运算明显加快。根据以上原理,笔者引用了其中的一个算法,叫镂空滤波算法,即每隔一行和列为“0”元素,gap=1,具体原理为:如图5为一个5×5模板,使用模板型均值滤波求P33的值,需要26 次的计算,可以滤除4×4以下的斑点和3×3的长条痕迹。如果把如图5中的阴影部分的像素值求均值来代替P33的值,相当于计算一个3×3的模板,计算次数是10 次,如果滤除4×4以下的斑点效果是一样的,那就直接减少了16次的计算次数,对提高均值滤波的运算速度意义重大。 图5 5×5模板镂空算法示意图 这种去除冗余数据的方法称之为镂空型均值滤波。计算公式为 (6) 式中:u=1,v=1,2,3,…,n;u=2,v=1,2,3,…,n;…。 根据式(6)计算方法,每隔一个像素取值计算,详见算法6。 算法6去除冗余数据滤波累积计算 temp=0 temp+=p(i1,j1) temp+=p(i1,j3) … temp+=p(i1,jn) temp+=p(i3,j1) … temp+=p(im,jn) 同样镂空滤波法可以应用到所有其他的计算方法中,可减少重复计算的应用公式为 (7) 式中:u=1,v=1,2,3,…,P1;u=2,v=1,2,3,…,P2;…;M为参与计算的像素点的个数。这些方法相当于把文献[2-7]和文献[8-10]的方法结合使用,同时比文献[8-10]更具有一般性。 (8) 根据加速理论和实现方法的分析,采用图3作为实验图像,分成5种数据量分别检测,如表1所示。处理的对象是滤除4×4点以下噪声点,所以需要采用5×5模板。实验用计算机配置:处理器AMD Athlon(tm)II X4 641 Quad-Core Processor 2.79 GHz,内存8 GB,64位操作系统。按照表2所列的6 种均值滤波算法分别运行,得到运行时间,结果如表3所示。为了能够对比整体加速趋势,实验选择了实际需要处理的金属轴表面缺陷线扫描图像(图3),分辨率为16 384×4 096,画出对应的加速算法的趋势图,如图6所示。 表 2 6 种均值滤波算法 表3 不同分辨率图像在不同算法情况下的均值滤波时间 图6 不同算法的运算时间 由表3可知:每一次方法的改进,速度都有不同程度的提高,只是每次提高的速度不一样。最快速度和最慢速度之比相差了10倍,模板型滤波改成镂空型滤波,在速度上也有比较大的提高,提高了2.7倍,和理论加速时间基本差不多。M3-1按列计算的算法中出现大数据时速度慢,小数据时速度加快的现象,而M3-2按行计算的时间却是正常加速。这就是由于CPU硬件内存结构中数据存放和检索所决定的[16-17]。数据加法计算在C语言编程中,不同的编程方式,速度差异是非常大。由实验数据中看出:数据累加方式和和加方式,速度相差1倍。对于不同分辨率的图片,加速并不是按照线性提高的,对于一个1K的图片,速度反而有所下降,所以针对不同的图片和硬件应选择不同的加速方法,才能获得最快的速度和最好的性价比。 通过计算机硬件系统来加速检测,效果虽然较好,但是硬件系统价格昂贵,在开发检测系统时性价比是必须要考虑的因素。通过研究不同算法来加速滤波,从而降低生产成本具有重要的现实意义。对于背景单一的高分辨率线扫描图像,提出了一种Atrous滤波算法,并将Atrous滤波算法和其他几种算法结合使用,可以显著提高计算速度,该算法也可以和其他加速算法结合使用,具有普遍适用的意义。笔者研究的均是串行加速计算方法,基于并行计算的加速是最直接的加速方法,并行计算方法可以采用全局内存、共享内存和线程束洗牌指令等数据存储算法来加速运算,有着非常广阔的开发空间。3.3 减少重复加法次数
3.4 去除冗余数据法


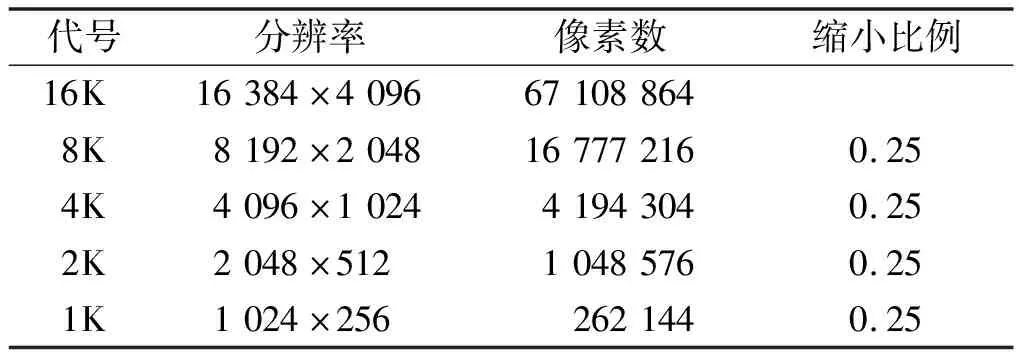


4 结果与分析


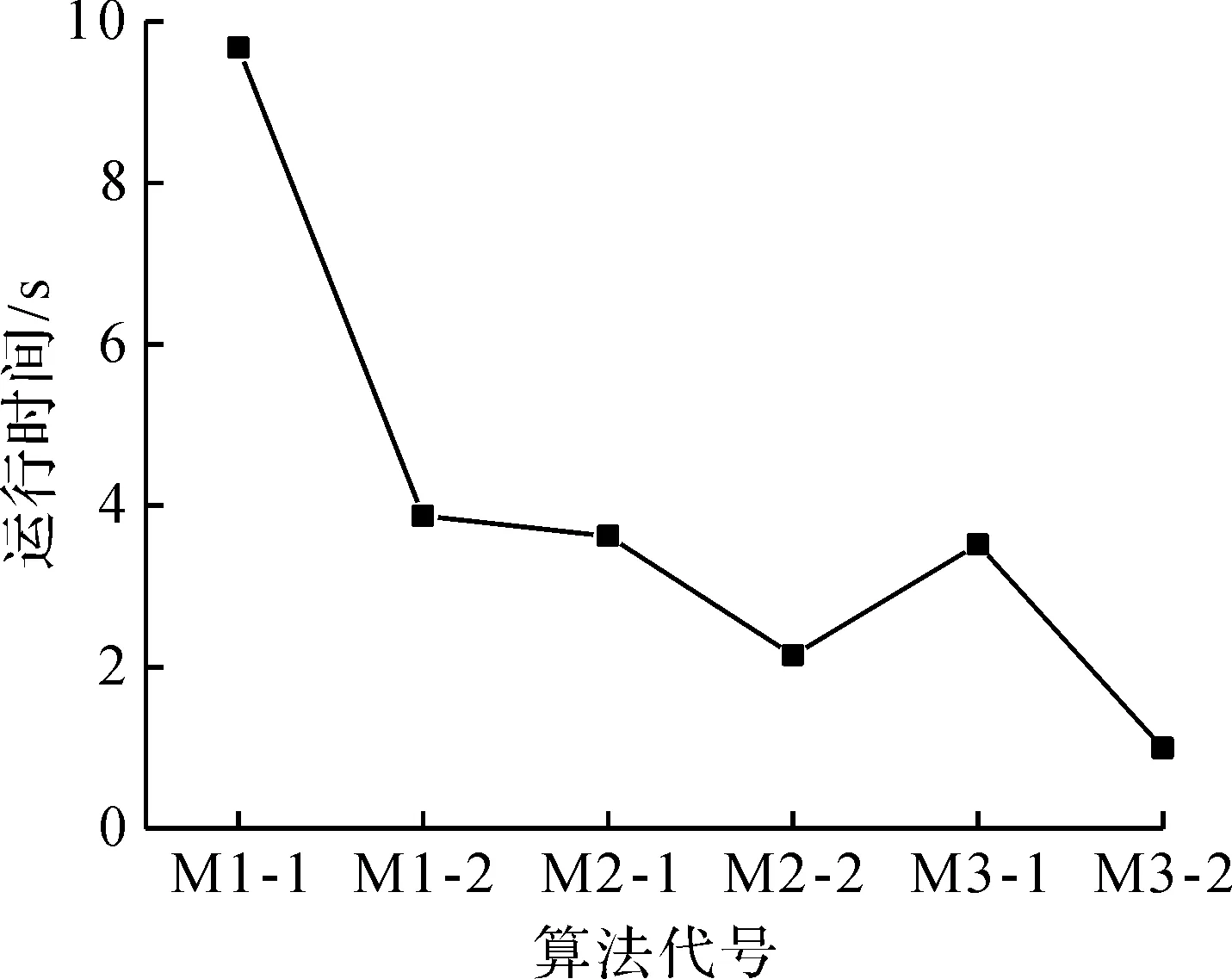
5 结 论
