融合邻域回归和稀疏表示的图像超分辨率重构

丁玉祥，卞维新，接 标，赵 俊

1.安徽师范大学 计算机与信息学院，安徽 芜湖241002

2.网络与信息安全安徽省重点实验室，安徽 芜湖241002

图像超分辨率（Super Resolution，SR）重建算法是利用观测到的低分辨率图像重建对应的高分辨率图像的过程，在军事、医学、遥感、计算机视觉等方面都有着重要的研究和应用价值。在日常生活中，获取高质量的图像受到诸如成像设备硬件成本、成像环境复杂等条件的制约。为了改善这一问题，图像超分辨率重建算法已被越来越多的研究人员关注。图像超分辨率重建采用软件方法，可以将低质量的图像重建成对应的高质量图像，既能够避免设备条件的复杂要求从而降低成本，也可以通过技术的不断发展使重建的质量得到提高。目前，基于单幅图像的超分辨率重建成为该研究领域的主要目标。图像超分辨率重建的方法主要有三类：基于插值的方法、基于重建的方法和基于学习的方法。

基于插值的算法是利用待重建像素与邻域像素之间的关系来预测待重建像素。这种方法具有算法复杂度低、运行速度快的特点，但是这种方法没有充分利用图像的高频信息，导致最终重建出的图像存在边缘、纹理缺失的问题，呈现的效果不是很好。

基于重建的算法是基于重建模型而来，通过加入先验知识，使得基于重建的算法在保持边缘方面有着较好的效果，但是关于图像的高频细节信息还是不能有效地被重建出来，低分辨率和高分辨率图像缩放尺寸越大，重建效果越差。常使用的方法有迭代反投影法（Iterative Back-Projection，IBP）[1]、最大后验概率法（Maximum a Posteriori，MAP）[2]和凸集投影法（Projections onto Convex Sets，POCS）[3]等。

基于学习的算法通过训练样本图像来学习低分辨率图像和对应高分辨率图像之间的映射关系，然后用学习到的映射关系来指导目标高分辨率图像的重建，这样可以重建出更多的高频信息。2004 年，Chang 等[4]结合流形的相关理论，提出了基于领域嵌入的超分辨率算法，克服了对样本的依赖。2010 年，Yang 等[5]利用自然图像的稀疏性，引入压缩感知理论，通过字典学习构建能够稀疏表示图像块的字典，然后通过该字典与线性规划求解得到的稀疏表示系数的线性组合得到重建图像，从而恢复图像的高频细节，取得更好的效果。在Yang的基础上，Zeyde 等[6]使用K-SVD[7]的方式训练字典，大大加快了字典训练时间，提升了学习的效率，重建的效果相较于Yang等的方法，效果得到很好的提升。之后，Timofte 等[8]则通过对字典稀疏训练得到的字典进行流形学习，在保证图像重建效果的前提下加快了图像的重建时间。李云飞等[9]在卷积神经网络超分辨率算法（SRCNN）的基础上提出一种多通道卷积的图像超分辨率重建算法（MCSR），生成的高分辨率图像质量较高，缺陷是算法时间复杂度较高。基于学习的算法在图像超分辨率重建领域正展现越来越强的优越性，成为当前主流的研究方向。

上述算法基本上都是对图像整体信息进行处理，没有关注图像的内部不同的信息特征。目前，一些研究人员[10-11]将低秩矩阵恢复理论应用于超分辨率重建算法，取得了不错的效果。受该类研究成果的启发，本文将提出一种改进的图像超分辨率重建方法。通过引入低秩矩阵恢复理论将高分辨率图像进行分解，得到图像的低秩部分和稀疏部分。其中，低秩部分含有图像的大部分信息，与低分辨率图像所含信息基本等同，可以通过压缩感知理论得到相应的字典对和稀疏系数，从而完成低秩部分的重建；稀疏部分含有少量的高频分量，通过寻找稀疏部分像素在对应于低分辨率图像上相同位置像素的映射关系来指导稀疏部分高分辨率图像的重建。提出算法依据图像信息特征的不同，将图像重建过程分为两路通道，利用容易被忽略的高频信息，改善重建算法的性能。实验结果表明，本文算法在峰值信噪比和结构相似性方面均有显著提升。

1 相关工作

1.1 低秩矩阵恢复理论

日常应用中所遇到的矩阵大多数都是低秩的或近似低秩的，这意味着矩阵的秩与矩阵的行数或列数相比较而言会很小。而平常接触的矩阵因为未知因素的干扰，原有的低秩性受到了破坏。于是为了恢复原有矩阵的低秩结构，可以将一个已知矩阵M 分解为一个低秩矩阵A 和一个稀疏矩阵E，其优化问题如下：

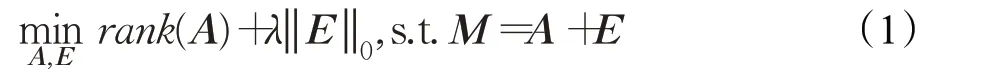
其中，‖ E ‖0表示稀疏矩阵E 的零范数l0，即E 的非零元素的个数。在目标函数中，rank(A)和‖ E ‖0均属于非线性非凸的组合优化函数，其求解属于NP-hard 问题。结合压缩感知的相关理论，可转化为凸优化问题：

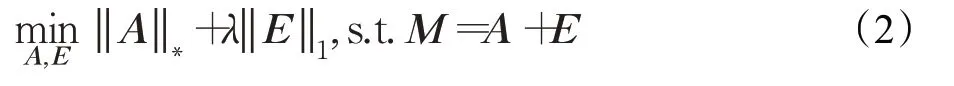
其中，‖ A ‖∗表示低秩矩阵A 的核范数，用来近似估计矩阵A 的秩；‖ E ‖1表示稀疏矩阵E 的l1范数；λ 是平衡因子，用于权衡矩阵的低秩性和稀疏性。

1.2 稀疏表示

Yang 等人[5]在研究图像超分辨率重建时引入压缩感知理论，将图像表示成一个过完备字典与稀疏系数的线性组合。通过寻求在低分辨率图像上的稀疏表示，然后利用稀疏表示得到对应的高分辨率图像。这种算法通过构建联合训练模型将低分辨率图像与高分辨率图像的相似性进行了强化，与传统方法相比，不但显著降低计算成本而且有很强的鲁棒性。其基本思路如下所示：

设x 是高分辨率图像X 的一个图像块，其对应的低分辨率图像块y 可由如下的降质模型得到：

其中，S 表示下采样处理，H 表示模糊处理。存在由一组高分辨率图像样本训练得到的过完备字典Dh，在Dh下，x 有唯一的最稀疏表示α：

其中，‖ α ‖0表示向量α 的零范数即向量α 的非零值个数，α 称为图像块x 的稀疏表示。根据式（3）可得相应的低分辨率图像块为：

其中，L=SH ，表示从高分辨率图像块到低分辨率图像块的一个映射矩阵，则低分辨率的字典为Dl=LDh。这表明高、低分辨率图像块在对应的过完备字典下有着相同的稀疏表示。因此，可以先求解低分辨率图像块y在低分辨率字典Dl下的最稀疏表示α ，然后再利用x=Dhα 即可重建出对应的高分辨率图像块x。

式（4）是一个NP-Hard 问题，稀疏表示α 的最优值很难求得。Donoho[12]已经证明，只要α 足够稀疏，则上述问题可以转化成L1范数最小化问题，因此式（4）可改写成：

根据优化理论，对低分辨率图像块进行稀疏表示的优化过程可描述为：

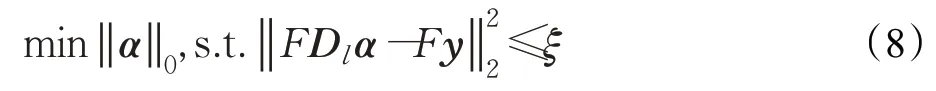
同样，可以将式（8）改写成L1范数的形式：

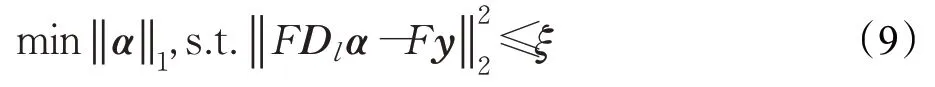
依据拉格朗日乘子法，式（9）可写为：

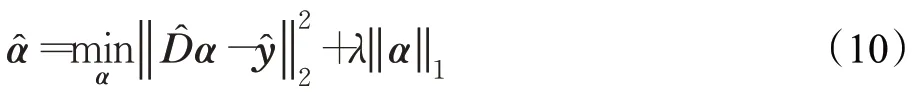
1.3 流形学习

流形学习方法是模式识别中的一种常用算法，研究的内容是从高维采样数据到低维流形结构的映射。其中，局部线性嵌入（Locally Linear Embedding，LLE[13]）是流形学习的一种。

LLE算法是一种非监督学习算法，它主要实现数据从高维空间到低维空间的非线性映射，并且这种方法能够较好地保持数据的局部特征。该算法假设在流形上的每个数据点和它邻域内的点在局部上都位于一个线性或近似线性的子空间上，那么其中的任意一点就可以用邻域内其他的点线性表示出来。而局部线性嵌入算法是一种典型的非线性降维方法，将这种算法应用在图像的超分辨率过程中，可以有效地对图像丢失的高频信息进行估计。LLE算法主要分为三步：

第一步，寻找每个样本点的K 个近邻点。

采用K 近邻法找到高维空间X 中每个样本点xi的邻域点集，由此找到关于样本点xi的k 个近邻点

第二步，计算权重wji：

进一步可得：

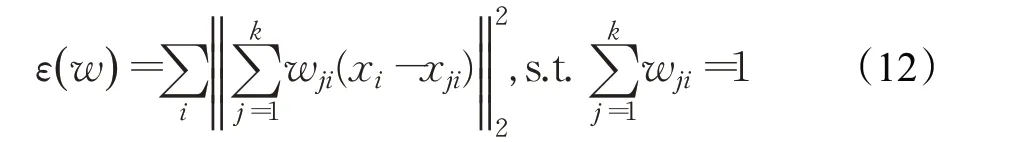
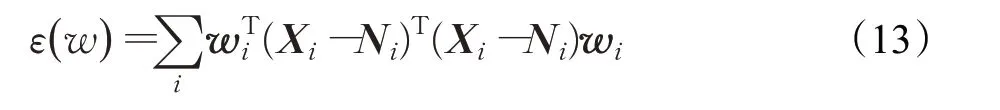
使用拉格朗日乘子法计算得到权值系数wi。

第三步，将高维空间X 映射到低维空间Y ，依据权值系数wi计算样本的低维嵌入。

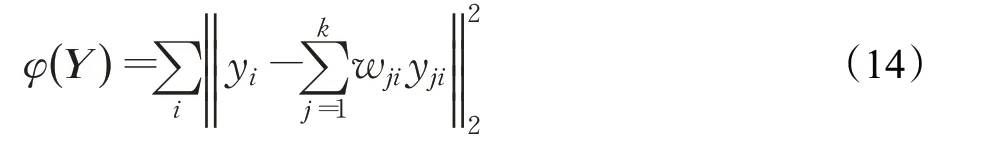
通过求解上述优化问题得到映射后的数据集Y 。

局部线性嵌入算法能很好地保持局部结构不变，且不需要迭代计算，降低了计算复杂度。通过将这种算法应用于稀疏部分的重建，可以减少训练量，很好地保持图像局部结构信息，从而在稀疏部分的重建上取得更好的效果。

2 图像超分辨率重建

为了充分利用图像内部信息特征，本文拟将图像的低秩性应用到图像的超分辨率重建，将低分辨率图像分别与对应的高分辨率图像的低秩部分和稀疏部分进行融合。然后用学习到的图像特征对待重建图像进行指导，得到最终的高分辨率图像。

由于图像具有低秩性，因此通过引入低秩矩阵恢复理论，可以将图像分解成低秩部分和稀疏部分。其中，低秩部分保留了图像的大部分信息，稀疏部分含有易缺失的高频分量。低秩部分可以通过其在低维空间的稀疏表示和学到的过完备字典的线性组合来表示。而图像的稀疏部分则可以依据在低维空间有相似的流形结构，利用相同的局部几何结构获取最优权重进行重建。提出的算法根据图像局部不同特征的信息在低维空间的投影，有效地重建高分辨率图像，避免了在重建过程中信息之间的干扰。

2.1 预处理

对高分辨率图像进行低秩分解，得到低秩子图像Ha和稀疏子图像He：

然后对高分辨率图像下采样得到低分辨率图像，再将低分辨率图像上采样到原高分辨率图像尺寸得到模糊图像Yl：

其中，L 表示高分辨率图像和低分辨率图像的映射矩阵，v 为加性随机噪声。将式（15）代入到式（16），得到：

对于低秩部分而言，它含有图像的大部分信息，为了学习它与Yl的之间的关系，可将含有少量信息的稀疏部分忽略：

由于图像的稀疏部分在低维空间有相似的流形结构，因此在局部几何结构上，可以只考虑稀疏部分在低维空间的投影。为了更好地获得稀疏部分在低维空间的投影，可将低秩部分忽略：

综合得：

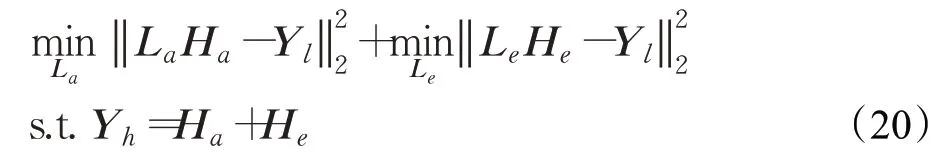
2.2 字典构建

本文对图像的低秩部分和稀疏部分分别采用稀疏表示和邻域嵌入方法进行重建。Chang等人[4]在LLE的基础上，提出基于邻域嵌入的超分辨重建方法（Neighbor Embedding+LLE，NE+LLE）。算法由两个阶段构成：首先将高分辨率图像训练集下采样得到对应的低分辨率图像训练集，由高低分辨率图像训练集构建高低分辨率块对训练集；其次，依据待重建低分辨率输入块，在低分辨率训练集内计算其K 个近邻块，依据邻域嵌入算法计算重建权重系数wi，再由对应的K 个高分辨率近邻块和权重系数wi得到重建的高分辨率块。黄福珍等人[14]基于Chang等人的工作，提出了联合局部约束的邻域嵌入方法，实现了人脸超分辨率重构。本文将不直接使用高低分辨率块对训练集用于邻域嵌入重建，而是借鉴字典学习方法，将学习到的高低分辨率特征字典用于邻域重建，从而能更好地表达图像稀疏部分的流形特征。

为了构建低秩部分高低分辨率耦合字典，将Ha的图像块集和对应的Yl的图像块集作为低秩部分字典学习训练集。同时为了提取稀疏部分的流形特征，将He的图像块集作为稀疏部分高分辨率特征字典学习训练集。

由于训练集pl的计算量较大，本文对其进行PCA降维，得到训练集，然后使用KSVD字典学习算法对进行训练，得到低分辨率字典Dl和稀疏系数Γl。

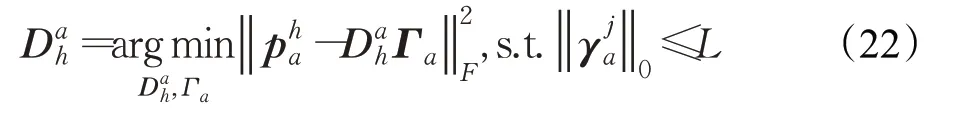
最终训练得到关于低分辨率图像、高分辨率图像低秩部分和稀疏部分特征的高低分辨率字典对

图1给出了本文字典构建过程的示例。

2.3 高分辨率图像重建

给出一个待重建的低分辨率图像Zl，假设该图像是通过与训练中使用的相同的模糊和缩小操作从高分辨率图像Yh生成，本文提出的高分辨率重建过程如下：

步骤1 对Zl进行上采样到指定尺寸的图像Yl。

步骤2 对图像Yl进行分块，得到图像块集

步骤3 对任一低分率图像块，依据字典Dl，由计算稀疏系数γlj。然后依据计算=，得到低秩部分高分辨率图像块，由此重建出高分辨率图像的低秩部分Ha。

步骤4 对任一低分率图像块，按照欧式距离最小，在低分辨率字典Dl中找到K 个近邻特征块集Nl=，对应的K 个高分辨率稀疏部分近邻块集为，计算LLE重构权值系数Wj=(wj1,wj2,…,wjk)：

图1 字典构建

邻域嵌入算法假设高、低分辨率空间具有相似的流形结构，从而可使用在低分辨率空间学习得到的LLE重构权重在高分辨率空间构建超分辨率图像，即低分率图像块对应的稀疏部分高分辨率图像块为：

由此重建出高分辨率图像的稀疏部分He。

步骤5 最后融合低秩部分图像Ha和稀疏部分图像He，重建最终的高分辨率图像Yh：

具体过程见图2。

3 实验结果比较与分析

3.1 实验参数设置

实验平台为处理器Intel Core i7-4810U@2.80 GHz的64 位Windows7 旗舰版，Matlab R2016a。为了提高重建质量，块重建采用重叠窗口技术。设定低秩平衡因子λ=0.45，字典元素个数为2 048，KSVD 迭代次数为40，低分辨率块尺度为3×3 像素，滑动窗口步长为2，邻域嵌入参数K=24。

3.2 算法性能比较与分析

为验证本文所提算法的有效性，将本文方法与几种典型的图像超分辨率重建方法NE+LLE[4]、Yang[5]、Zeyde[6]、ANR[8]、GR[8]和MCSR[9]做了实验比较，通过使用图像评价中最常用的PSNR和SSIM指标进行客观评判。其中PSNR 表示峰值信噪比，而SSIM 表示结构相似性。其表达式分别为：

本文首先验证该算法在测试集Set14上的效果，图3给出了一组实验结果。通过实验结果，不难发现本文算法在PSNR和SSIM上都有着明显的提升。为了验证提出算法在不同尺度上的表现，在测试集Set5上对不同尺度图像的超分辨率重建进行了测试，放大尺度分别为2、3和4，表1给出了PSNR和SSIM的量化实验结果，不难发现在进行图像超分辨率重建的过程中采用不同的放大尺度，提出的算法都显示出不错的效果。

为了进一步验证提出算法的性能，本文给出了一组超分辨率重建结果的可视化实验，如图4 和图5 所示。由图可以看出：双三次插值重建对图像噪声几乎没有作用，重建结果相当模糊，缺失了大量的高频细节信息；Yang 等的算法通过先验重建图像的高频信息，较之于插值算法性能有所提升，重建出了原始图像的大部分信息，但是重建图像的边缘不够清晰，有些模糊；Zeyde算法的重建图像较Yang 的边缘信息更优，但是重建出的图像带有阴影，影响了视觉效果；NE+LLE 算法的重建图像具有不错的细节信息，但是颗粒感强烈，影响视觉；本文算法融合稀疏表示和LLE 算法对图像进行超分辨率重建，使得重建图像边缘清晰，视觉效果更好。

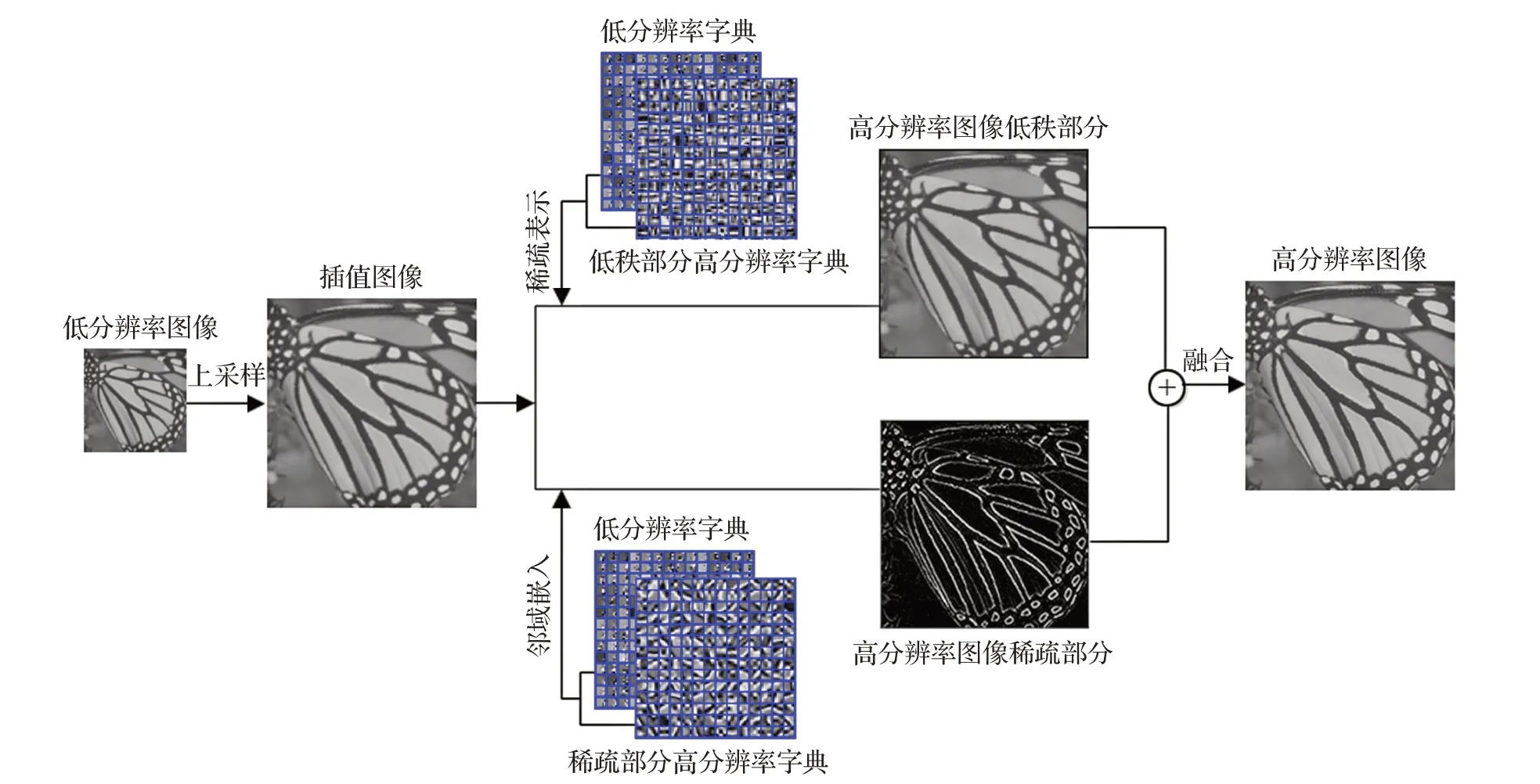
图2 图像超分辨率重建

图3 测试集Set14上放大尺度为3的PSNR和SSIM

表1 测试集Set5上不同放大尺度的PSNR和SSIM

图4 放大尺度为3时butterfly各算法重构效果比较

图5 放大尺度为3时foreman各算法重构效果比较

4 结论

针对图像超分辨率重建算法忽略图像内部结构信息的原因，本文通过采用低秩矩阵恢复理论将分别对图像的低秩部分和稀疏部分进行重建，最后融合得到最终的高分辨率图像。对于原高分辨率图像，首先进行低秩分解，得到含有原始图像大部分信息的低秩部分，和含高频信息的稀疏部分。对低秩部分、稀疏部分和原始图像对应的低分辨率图像进行联合训练，构建对应的特征字典对。对待重构的低分辨率图像分别基于学习到的特征字典对采用稀疏表示和邻域回归重建出图像的低秩部分和稀疏部分，最后将重建的低秩部分和稀疏部分融合得到高分辨率图像。实验结果表明，本文算法的重建结果相较于多种超分辨率方法，得到的图像边缘和结构信息更加丰富，而且在客观评价标准PSNR 和SSIM上获得了不错的提升。