基于重要性采样的广义霍夫变换算法

宋晨菲， 张 彤

(桂林电子科技大学 机电工程学院，广西 桂林 541004)

物体检测是机器视觉技术在工业领域的重点研究方向，广泛应用于工件检测、电子元器件检测，目的是从一幅图像中根据模板图检测目标是否存在并确定目标的准确位置。基于灰度的物体检测方法计算量过大，且易受光照环境的影响，不适用于实时应用。模板匹配的方式对不同物体存在旋转、缩放、遮挡等问题时适应性不好[1]。霍夫变换是一种基于二值图像检测直线或圆的全局性检测方法。广义霍夫变换(generalized Hough transform，简称GHT)算法[2]是霍夫变换算法的改进，用于从图像中检测出任意轮廓边界的物体，在图像目标识别应用中备受关注。在待检测图像中若物体存在尺度变化、旋转变换或噪声点时，算法的计算时间和内存将极大增加，这是广义霍夫变换在物体检测研究及应用中遇到的主要困难。为此，人们研究改进的GHT算法。Fung等[3]提出了随机广义霍夫变换(random GHT，简称RGHT)算法，减少了霍夫空间的投票数目，降低了时间复杂度，但该算法的检测精度在目标物体发生缩放变换或图像存在噪声时受到很大影响。胡方明等[4]将随机广义霍夫变换和模糊推理系统融合，提出模糊随机广义霍夫变(fuzzy random GHT，简称FRGHT)算法，但当被检测物体不规则边缘占比过大且有旋转变换时，算法的时间效率明显降低。雷芳等[5]采用多层图像金字塔思想对图像进行由粗到精的匹配。王彦等[6]根据设定的阈值，记录目标物体相关位置并通过GPU加速来检测多目标图像，但图像中存在较多噪声时精度明显降低。针对以上问题，提出一种基于重要性采样的广义霍夫变换(ISGHT)算法。

1 算法基本思想

视频目标跟踪问题与图像中物体检测问题有一定相似性，它们都需要在目标图像中寻找某个模板物体[7]。为了较好地解决目标图像中物体易受旋转、放缩及噪声干扰影响的问题，根据边缘点显著性，提取特征边缘点用作采样样本，以相似性计算权重，并更新粒子区域，最终通过多分辨率下广义霍夫变换投票，精确确定物体位置。

1.1 特征边缘点检测

特征点检测是物体检测的重要部分，以边缘点坐标、切线方向、梯度幅值、梯度方向等属性作为边缘点显著性的筛选标准。

1)边缘点位置。某边缘像素点(xi，yi)与附近点间的距离为

Ds(xi,yi)=max(|xi-xi-1|,|yi-yi-1|)，

(1)

某边缘点附近k个点的距离为

(2)

2)切线方向。若待测图像边缘某点为(xi，yi)，其相邻点为(xi+1，yi+1)，则斜率

(3)

由2点位置计算的斜率易受噪声的影响，因此选用边缘点附近的多个点计算斜率。首先以该点为中心，以该点两侧各2个边缘点共5点进行直线拟合，再计算边缘点斜率(若附近边缘点数目低于阈值，则可判定为噪声点)，最后得出该点的切线方向

Dt=arctanSl。

(4)

3)梯度幅度及方向。对于检测目标，若所选择的邻域面积过小，则噪声更易对梯度计算产生影响。本算法所选的高斯滤波器为二维高斯函数的偏导数，其梯度[8]为

(5)

设gx、gy分别为为x、y方向梯度幅值检测算子,通过卷积运算，方向梯度幅值为

fx=f*gx,fy=f*gy。

(6)

进而可求得每个点的梯度幅值gr和梯度方向Dg：

(7)

(8)

4)邻域野点抑制值。通常目标物体真实边界的边缘点附近不会出现其他的靠近该点的连续长边缘，即若某一点附近有越多的边缘点或其附近的边缘长度越长，则该边缘点就越不可能为目标物体边界。因此，某边缘点附近与其靠近但不连接的点即为野点。为了描述邻域野点抑制值的距离加权，设中心环境高斯差分函数FGD为

(9)

其中σ1和σ2为2个高斯分布函数的标准均方差，分别表示外周区及中心区的面积，取σ1=4σ2。将距离加权函数Wd进一步归一化处理，

(10)

其中函数N(t)为

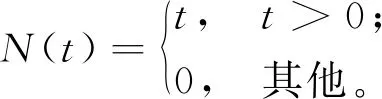
(11)

图1为野点抑制距离加权函数示意图。边缘点的邻域野点抑制值为

Rwp=f(xi,yi)*Wd(xi,yi)，

(12)

其中f(xi，yi)为点(xi，yi)被去除后的剩余边缘。

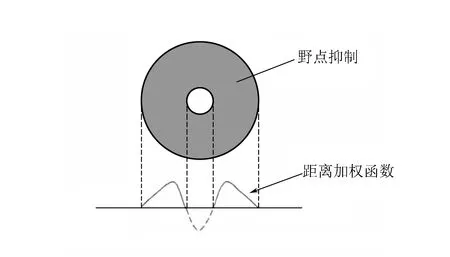
图1 野点抑制距离加权函数

综上所述，边缘点的显著性可由该点位置、切线方向、梯度幅度及方向、邻域内野点数目等决定。经理论分析及实验可知，边缘点显著性衡量因素为：

1)边缘点与附近像素点距离较近；

2)边缘点的梯度方向与切线方向垂直；

3)边缘点领域内野点较少；

4)边缘点所在的边缘长度较长。

综上定义显著性Sp计算式为

(13)

其中：wi为衡量各特征重要性的权重因子，权重因子越大，该特征对某种形状物体轮廓的显著性影响越大，通常取w1=w2=w3=w4=0.25；σi表示控制边缘点显著性变化速率的量，一般取σ1=σ2=σ3=σ4=0.5；τi为各分量的归一化系数。

1.2 重要性采样

只能获得来自于采样分布g(x)而并非期望分布f(x)的样本时，可采用重要性采样技术来估计期望分布f(x)[9]。对于离散随机变量θ，其采样分布为g(θ)，θ∈Ω，其中Ω为θ的采样空间，采集样本θ1，θ2，…，θT。g(θ)取决于变换因子c[10]，

g(θ)=f(θ)/c。

(14)

样本中每个观测值为

(15)

一旦采样机制确定，采样分布g(θ)也随之确定[11]。然而不管采样机制复杂与否，对g(θ)的准确计算都十分困难。假设采样分布是近似均匀的(这一假设对广义霍夫变换的性能影响很小)，式(15)可简化为

(16)

采样对于广义霍夫变换算法的效果有很大影响。本算法采用的期望分布为

f(θi)=α(θi)β(θi)γ(θi)，

(17)

其中：α(θi)为位于目标物体边缘的点数估计函数；β(θi)为采样点集的拟合优度估计函数；γ(θi)为目标物体与模板物体相似性估计函数。

点数估计函数α(θi)为

(18)

其中：N为边界点数目；rj为某边缘点与参考点之间的距离；W(rj)为模糊隶属函数，它可以是线性函数、阶跃函数、高斯函数等。为了获得较好的检测结果，选用高斯函数，

(19)

其中R为采样点集中参考点到最远的边缘点的距离，σ=R。

拟合优度估计函数β(θi)为

(20)

其中：pi为与参考点距离在R以内的准边缘点的数目；ci为模板物体边缘点的总数；βth为阈值。

相似性估计函数γ(θi)由边缘点位置、梯度相位差异性计算得到：

γ(θi)=PlocPphaDh,

(21)

其中Ploc、Ppha、Dm分别为边缘点位置差、梯度相位差及弥补形状缺失的距离度量。

1)位置差。边缘点位置差为

(22)

其中De为两点的欧氏距离，

(23)

若a与b两点是对应点，则De值较小;若两者位置差异较大，则De值较大。σloc为评估位置不确定性的参数，该参数的取值范围越小，即意味着对两边缘点的位置间差异容忍度更低，则检测的精度越高，经实验一般σloc取值范围为[1，3]。若De趋向于0，则Ploc趋于1，a、b两点是对应的准边缘点；若Ploc趋于0(De值较大)，则两点不是对应点。

2)梯度相位差。边缘点a与b相位差为

ωp=ωb-ωa，

(24)

其中ωa、ωb分别为为模板图像中边缘点a及目标图像边缘点b的梯度相位。当两点在梯度相位上ωb=ωa，即ωp=0，此时相似性为1。当ωp=π/3时，a和b两点的梯度相位差为下限值，相似性为0。梯度相位差Ppha的计算式为

(25)

其中u(x)为正态分布函数。

3)弥补形状缺失影响的距离度量。由于工业检测中可能存在工件破损或被遮挡等问题，以及可能存在不同程度噪声干扰，根据平均Hausdorff距离的思想，基于上述相似性约束，将2个点集根据相似性度量值由高到低排序，定义一种距离度量方法,

(26)

其中N=τK，K为目标图像中点数和，τ为遮挡系数，一般取0.7～0.8。由式(26)可知，由于遮挡、噪声干扰产生的相似性影响降低，在噪声密度较高时也能有较好的效果。

1.3 基于加权多分辨率的广义霍夫变换算法

广义霍夫变换算法基于霍夫空间投票规则，其投票元素为轮廓上的边界点，在参数空间中的投票位置由事先定义的参考点和投票机制确定，通过投票来判定目标的存在与否。

设Xr=(xr,yr)是待检测任意形状的目标物体轮廓内一参考点，X=(x,y)是该物体轮廓边界上的任意一点，Xr和X之间的差矢量为r=Xr-X；如图2所示，α为r与水平方向夹角，φ为点(x,y)处的梯度值夹角。

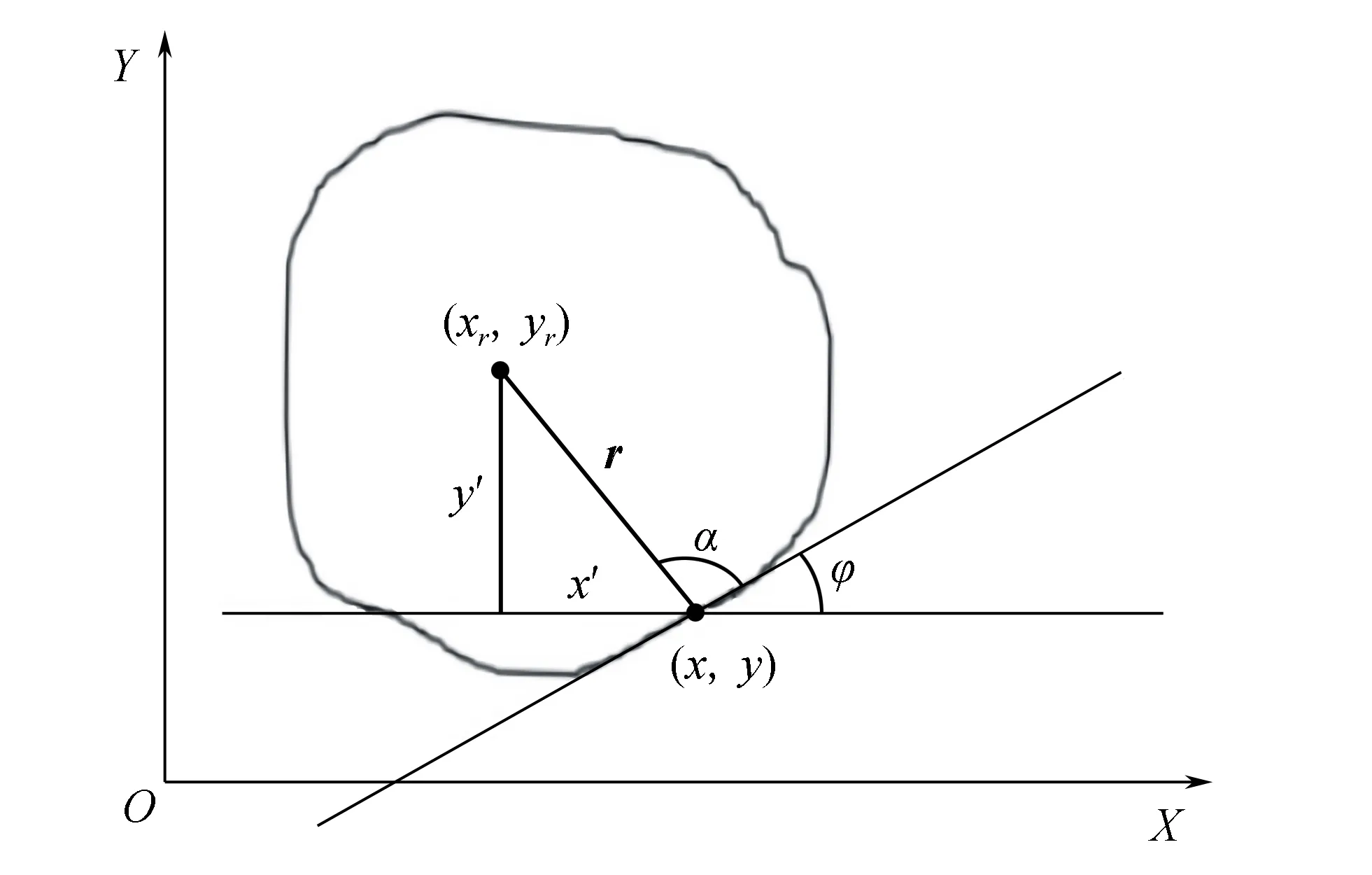
图2 广义霍夫变换原理图

由图2可得，

xr=x+rcosα，yr=y+rsinα。

(27)

r、α、φ可共同确定一个边缘点，因此将所有边缘点(r，α)参数按φ为条目存入一表项中。表1为建立模板查找表R-table。

表1 模板图像建立的R-table

在目标图像检测阶段，可利用待检测图像的边缘点坐标以及梯度角相关信息通过查找预存的R-table在霍夫空间投票来确定参考点的位置。但是待检测图中目标物体可能存在缩放或旋转变化，对于这些影响，R-table需要进行对应的变换，根据预设变化的范围以二分查找方法确定缩放比例及旋转角度。若存在遮挡则需要降低投票阈值。统计投票所得的不同参考点位置的匹配数目确定峰值，以找出目标物体的最佳匹配参考点的位置。

为了减小霍夫空间，提升目标匹配的效率，将广义霍夫变换结合金字塔模型进行多分辨率分析[12]。金字塔模型是将图像分为不同尺度，顶层为Ln，底层L0为原图像大小，由于缩小了图像尺寸提升了算法计算速度，但边缘点较少可能使得有些结果忽略了物体的某些局部轮廓特性，使得匹配误差产生的可能性增大。为此，采用多尺度加权匹配的方法，将除L0外的多层图像经过本算法处理后得到的目标物形状参数为θi((xc,yc)，s，θr)。加权目标物形状参数

(28)

由于限定了缩放系数与旋转角度的搜索范围，由此极大地减小了霍夫空间。wi越大，则该尺度对于融合结果的影响越大。

GHT算法的主要缺陷在于高维累加器中对目标图像像素点的无差别投票产生了巨大计算量，因此很难满足实时性要求。并且在目标图像背景环境复杂或图像中存在噪声的情况下很容易受到无效点的干扰，精度较难保证。为此，基于显著性特征边缘点缩小搜索空间减少投票元素，将其置于重要性采样框架中，并结合加权多分辨率分析，提出融合重要性采样的广义霍夫变换算法。具体算法步骤为：

1)根据边缘点性质检测特征边缘点，获取模板边缘点数M。对目标图像下采样获得多层图像L1，L2，…，Ln，从顶层Ln开始检测。

2)对当前图像层Li获取边缘点数目N，边缘点集A。

3)在点集A中采样T=τN(τ为遮挡系数)个点获取关于模板物体的随机样本，若图像中存在k个模板物体，则T=kτN。

4)根据目标分布函数计算重要性权重ωi。

5)根据重要性权重大小排序，对t=τN个点通过广义霍夫变换投票。

6)确定随机样本投票后的准边缘点是否达到设定的阈值S(模板边缘点数τM)。若仍未达到阈值，则返回步骤3)重新采样；若达到阈值，则进入下一层Ln-1返回步骤2)。

2 实验结果及分析

为了验证本算法的有效性，在计算机上针对多组存在旋转、缩放变换或存在噪声干扰实拍图像进行实验，衡量物体检测算法性能指标主要为计算时间、匹配误差。衡量检测精度的误差均值为

(29)

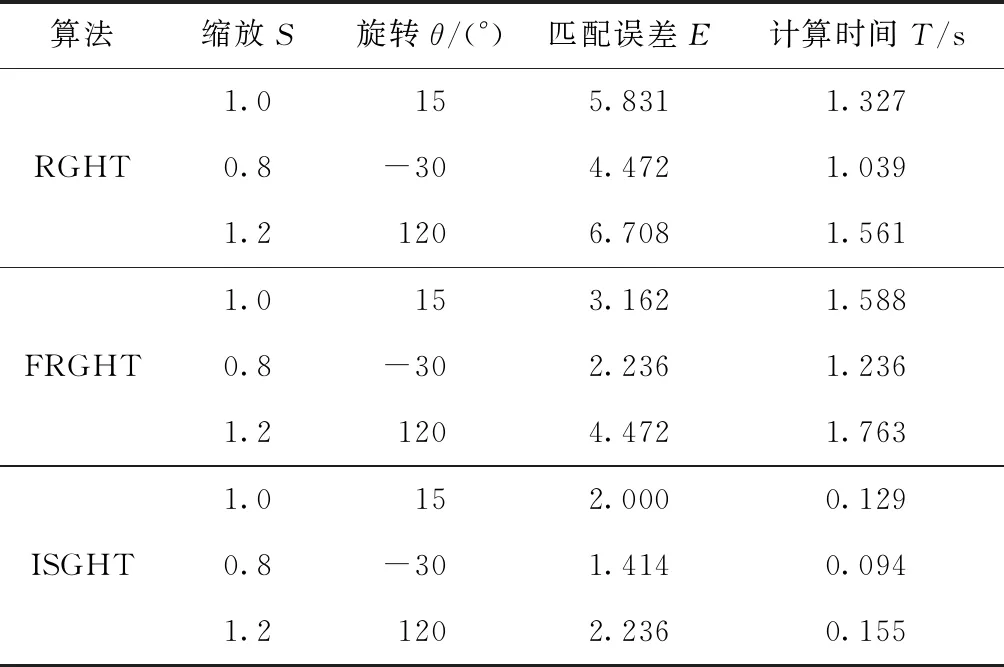
表2 ISGHT算法与FGHT算法、FRGHT算法实验结果

图3 噪声对算法精度的影响

图4 噪声对算法计算时间的影响

图5 缩放比例对算法精度的影响

图6 旋转角度对算法精度的影响

图7 本算法部分实验结果

传统GHT检测算法的主要缺陷在于算法需要对整幅目标图像点无差别投票,导致计算量过大，时间复杂度过高。并且在目标图像背景环境复杂或图像中有多物体的情况下很容易受到干扰，精度较难保证。显著性边缘点的确定减小了搜索投票空间，大大减少了对于边缘点的投票计算量，并降低了复杂背景及噪声的影响。基于重要性采样的ISGHT算法根据目标分布权重投票并结合加权多分辨率分析，减小了霍夫空间，提升了算法效率，相对于RGHT等算法也保证了精度，并且在物体缺失、被遮挡时也有不错的效果。由表2、图3～7可知，本算法相对于RGHT、FRGHT算法，不仅保证检测精度，降低了计算量，提高了检测效率，并且在旋转、缩放变换及物体被遮挡情况下也能有很好的效果。

3 结束语

将广义霍夫变换算法置于重要性采样框架中，提出了一种新的物体检测算法，根据显著性检测特征边缘点，由目标物体与模板物体各边缘点的相似性计算重要性权重，采用多分辨率分析的方法进行霍夫投票确定目标位置。实验结果表明，提出的ISGHT算法能够更快速准确定位目标物体，受不同程度噪声的影响有所降低，且综合局部特征与全局特征在放缩、旋转变换下都有较好的检测效果。在制造业工件检测、芯片检测中有较好的应用价值，进一步优化后可以应用于嵌入式设备。