异种铝合金搭接焊接头的疲劳特性及其寿命预测

许 诺 金 一 张 梅

(1.上海汽车集团技术中心, 上海 201804； 2.上海大学材料科学与工程学院，上海 200444)

轻量化是汽车的发展趋势。铝制汽车构件具有一系列优良特性，如密度小，比强度和比刚度高，抗冲击性能、耐蚀性好，表面易着色等，在汽车工业得到了广泛应用[1]。

很多铝制汽车构件是焊接而成的。然而由于铝合金焊接时易氧化和吸气、导热快以及易变形等，与钢相比有较大差异，较难焊接。为此铝合金的焊接都采用较先进的焊接设备、焊接工艺及焊接材料，铝合金的焊接技术也在不断发展和完善。

Fronius公司在2002年开发了冷金属过渡(CMT, cold metal transition)技术，它是基于短路过渡电弧的“专业系统化中断”技术实现“热—冷—热—冷”交替的焊接工艺，可减小电弧压力和能量输入，是一种全新的短路过渡技术，实质上是熔化极惰性气体保护焊(MIG, metal inertia gas)的一种。与普通MIG焊相比，CMT焊具有无焊渣飞溅、热输入较低等优点[2- 3]，适合焊接薄板或超薄板，在铝合金焊接中应用广泛。

本文研究用合金是最常用的6082变形铝合金和A356铸造铝合金。虽然有研究涉及到了这两种材料的热处理工艺、组织和性能等[4]，现有文献也有一些关于采用CMT工艺焊接变形铝合金的报道[5- 8]，但对于6082变形铝合金与A356铸造铝合金的焊接接头性能的研究报道较少，尤其是有关异种铝合金焊接接头疲劳特性的研究十分匮乏。目前，为实现汽车轻量化，在变形铝合金与铸造铝合金的焊接方面尚存在诸多问题，亟待解决。

1 试验材料及方法

1.1 试验材料

对A356合金板和6082合金板进行搭接焊，而后从搭接焊接头上切取疲劳试样进行应变疲劳试验，对试验数据进行处理，以获得搭接焊接头的应变疲劳特性参数。

两种铝合金板的尺寸均为2.5 mm×200 mm×200 mm，采用CMT工艺进行双焊缝搭接焊，焊后去除焊缝余高，并按国标进行取样，分别在起弧与收弧预留25 mm处取样。图1为搭接处厚度为2.5 mm的双搭接焊接头试样的示意图和实物，将焊缝中心置于平行段中部，目的是尽可能考虑到焊缝与焊接热影响区对其疲劳性能的影响。考虑到搭接试样的特殊性，为防止试样弯曲，设计了相应的疲劳试验专用夹具，在疲劳试验中装配。试验根据GB/T 26077—2010《金属材料轴向等幅低循环应变疲劳试验》进行。

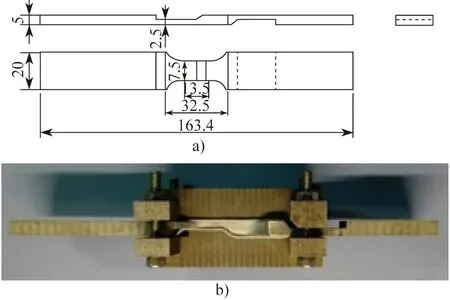
图1 A356- 6082合金搭接焊接头低周疲劳试样示意图及试样夹具Fig.1 Low- cycle fatigue test specimen taking from the lap- welded joint of the A356 and 6082 alloys and its fixture

1.2 试验标准和设备

按GB/T 26077—2010和GB/T 15248—2008《金属材料轴向等幅低循环疲劳试验方法》进行试验数据的采集、整理及后续的绘图和曲线拟合，然后确定各项参数。试验在MTS电液伺服疲劳试验机上进行。

1.3 试验方法

低周疲劳应变幅分别为0.2%、0.265%、0.4%、0.465%、0.535%，每个应变幅至少重复试验3次。按GB/T 26077—2010对数据进行曲线拟合后得到接头的疲劳参数σf′、b、εf′、c、K′和n′。

2 原始数据及其处理

2.1 低周疲劳数据

首先导出试验机采集到的力和位移的数据，采用式(1)和式(2)将其换算成应力和应变。

σ=F/S

(1)

ε=1-(l0×εt)/(2la)

(2)

式中：F为采集到的力，S为试件的横截面积，l0为位移中值，εt为试件的总应变，la为位移幅值。

根据GB/T 26077—2010拟合疲劳寿命曲线，通过滞后曲线(见图2)得到塑性应变幅值， 弹性应变幅值由总应变幅值与塑性应变幅值相减得到。试样的总应变则通过图像的采集系统计算得到，根据式(3)便可计算出试样的弹性应变幅值。

Δεe/2=εt/2-Δεp/2

(3)

图2 滞后曲线示意图Fig.2 Schematic diagram of hysteresis loop

2.2 低周疲劳试验原始数据

表1为A356- 6082合金搭接焊接头的低周疲劳试验原始数据。

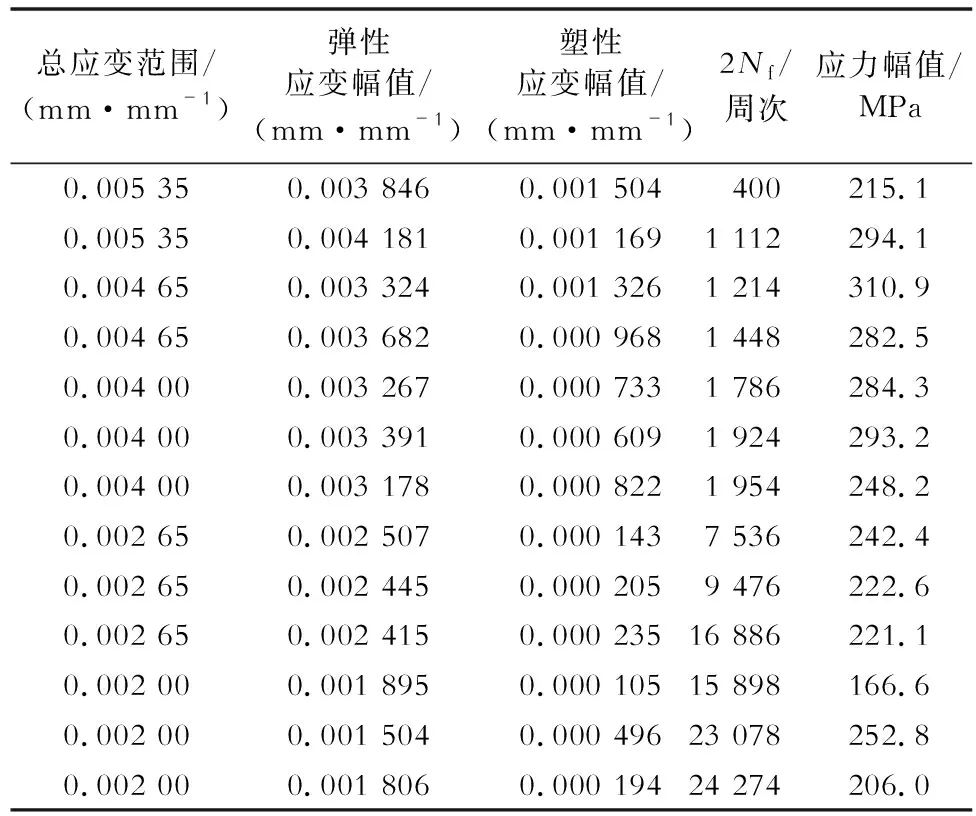
表1 A356- 6082合金搭接焊接头低周疲劳试验原始数据Table 1 Original low- cycle fatigue test data on lap- welded joints of the A356 and 6082 alloys

2.3 低周疲劳特性参数

根据疲劳试验的特点，应力幅值Δσ/2、疲劳强度系数σf′和疲劳寿命Nf之间存在如下关系：

Δσ/2=σf′+×(2Nf)b

(4)

疲劳强度系数σf′、疲劳强度指数b、弹性应变幅值Δεe/2和疲劳寿命Nf存在以下关系：

Δεe/2=(σf′/E)×(2Nf)b

(5)

对式(5)两边求对数,得：

log(Δεe/2)=log(σf/E)+blog(2Nf)

(6)

根据式(6)可将log(2Nf)和log(Δεe/2)拟合成一条直线，即2Nf—Δεe/2，其中b为斜率，log(σf/E)为截距。

同理，疲劳延性εf′、疲劳延性指数c、塑性应变幅Δεp/2和疲劳寿命2Nf存在以下关系：

Δεp/2=εf′×(2Nf)c

(7)

循环强度系数K′、循环应变硬化指数n′、塑性应变幅值Δεp/2和应力幅值Δσ/2存在以下关系：

Δσ/2 =K′×(Δεp/2)n′

(8)

对式(7)和式(8)两边取对数，分别可以得到斜率为c和n′、截距为logεf′和logK′的直线，即Δεp/2—2Nf和Δσ/2—Δεp/2曲线。根据GB/T 26077—2010采用恒应变频率控制方法进行试验，频率为1 Hz。

3 低周疲劳特性

根据低周疲劳数据处理标准以及Mansion- Coffion(M- C)方程(式(4)、(5)和(7))，对试验数据进行线性曲线拟合,得到的结果如图3和图4所示，并将拟合得到的低周疲劳特性参数列于表2。通过疲劳参数的导入，采用数值模拟软件Ansysncode预测疲劳行为，并进行试验验证。

图3和图4为搭接焊接头试样的循环应力- 应变曲线、应变- 循环次数曲线以及根据M- C方程拟合的参数曲线。

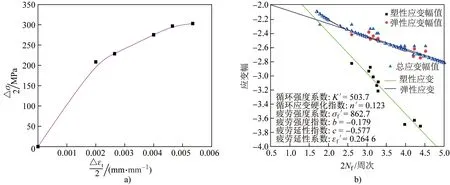
图3 循环应力- 应变曲线(a)和E- N曲线(b)Fig.3 Dependences of cyclic stress on strain (a) and of E on N (b)

图4 △εp/2-2Nf关系(a)和△εe/2-2Nf关系(b)Fig.4 Dependences of △εp/2 on 2Nf (a) and of △εe/2 on 2Nf (b)

表2 疲劳特性参数汇总Table 2 Summary of the fatigue characteristic parameters

4 铝合金副车架疲劳寿命预测及验证

4.1 疲劳寿命预测

图5为前副车架的有限元模型。铝合金副车架车身连接为硬连接，采用约束法求解准静态应力。铝合金副车架主要风险区域为焊缝区，主要包括横梁与纵梁连接处的焊缝、转向机支架处焊缝和稳定杆支架根部焊缝。

铝合金焊缝疲劳性能采用静态工况预测，求得峰值载荷下的应力后，根据应力曲线进行线性叠加，通过NCODE软件采用E-N曲线求解。通过优化支架结构和焊接走向，有效减少了疲劳损伤，如图6所示，优化结构的最大损伤为0.22， 低于软件设定的开裂门槛值2.5，满足设计要求。

图5 前副车架有限元模型Fig.5 Finite element model of the front sub- frame

图6 前副车架焊缝的疲劳损伤分布Fig.6 Fatigue- damaged distributions of welding seam for the front sub- frame

4.2 验证

对结构优化的前副车架进行单通道台架试验，以验证预测的疲劳寿命。图7为进行疲劳台架试验的前副车架。试验结果表明，4组试件试验至3倍以上的目标寿命均未开裂。此外，将按优化方案焊接的前副车架装车，通过了道路试验场100%验证，均未开裂。

图7 台架试验中的前副车架Fig.7 Front sub- frame during bench test

5 结论

(1)试验铝合金A356- 6082搭接焊接头的应变疲劳特性如下：

Δεp/2=503.7×(△εp/2)0.123，

Δεp/2=0.264 6×(2Nf)-0.577，

(2Nf)-0.577。

(2)采用试验获得的疲劳特性参数进行构件的疲劳仿真分析，前副车架台架疲劳损伤符合要求，台架试验结果表明，CAE寿命预测结果与实际结果吻合。前副车架装车通过了道路耐久性验证，证实采用试验所得的疲劳特性参数预测的疲劳寿命准确，预测方法可靠。