不完整数据下制动软管可靠性分析与应用

李权福，操 琴，李 琦，蒋增强

(1.神华铁路货车运输有限责任公司，北京 100011;2.北京交通大学 机械与电子控制工程学院，北京 100044)

铁路货车的提速和重载，对货车的可靠性和安全性提出了更高的要求[1]。其中，货车制动系统直接影响货车的安全性。制动软管作为制动系统中的关键零部件，其作用是将货车间制动主管连接起来，保证制动的及时性，减少对车钩等零部件的冲击。在列车运行过程中，制动软管会受到货车间的压缩力和牵引力的作用，加上环境影响，易造成部分制动软管产生裂纹、腐蚀和泄露等故障[2]，影响行车安全。因此，开展制动软管的可靠性分析，对整车安全及零部件的维护维修具有重要意义。

由于现场管理相对粗放，制动软管的寿命数据存在不完整、不精确的情况，可以归纳为截断和删失两种。关于含截断删失数据的可靠性研究，如林珊屹[3]针对删失数据类型，利用半参数方法建立了广义指数Cox比例风险模型，运用Newton-Rapson算法对参数进行估计，并通过艾滋病治疗临床试验验证了该方法的有效性。王灵芝等[4]采用平均轶次法对现场随机截断数据进行预处理，建立关键零部件的可靠性分析模型，并确定各设备的最佳维修周期，结果表明该方法对各种样本量均具有很好的拟合精度。张马兰[5]采用多参数分阶段非线性的融合方法计算了发动机性能指标,结合粒子滤波思想建立了发动机的性能衰退模型,借助粒子滤波预测估计了模型的时变参数,有效预测了发动机的剩余寿命,有利于航空发动机剩余寿命预测方法的研究。刘思严[6]针对左截断右删失的数据类型，以二参数Weibull分布为例，提出参数两步迭代法，并通过实例验证了参数两步迭代法估计尺度参数的可行性。徐永红等[7]针对半混合删失数据，即同时包含精确数据、右删失和严格删失区间数据，利用混合插补法将右删失数据插补为区间删失数据，进而展开分析，结果证明相对于SC(self-consistent)算法，混合插补法有更高的精确度和更好的稳健性。YANG等[8]提出了一种基于综合数据的参数经验似然估计方法，并构造了相应的参数置信区间推导公式，仿真研究表明与正态逼近方法相比，该方法在覆盖概率和置信区域面积方面有更好的效果。

综上可知，现有方法主要针对具体研究对象，应用非参数或修正方法进行可靠性参数估算，有一定的局限性。因此，笔者依据失效模式和影响分析(failure mode and effect analysis，FMEA)定位零部件的主要失效模式，根据截断删失数据类型，构建制动软管失效发生时间的概率分布模型，结合最大似然估计与自举法，得到参数的点估计与区间估计，进而预测制动软管的剩余使用寿命，并据此开展基于成本优化的制动软管报废周期优化与基于失效区间的制动软管物料管理研究，以期为零部件预防性维修和更换提供依据。

1 失效模式和影响分析

FMEA是一种确定零部件失效模式及原因的系统化分析方法[9-10]。目前，制动软管检修工艺包括外观检查、外部清洗、风压试验、水压试验、涂打标记和储存等步骤。制动软管的主要失效模式为制动软管破损和泄露，其易发性和危害性为中级，需要进行外观检测和密封试验检查。制动软管的失效模式还有如制动软管角度不正位，制动软管卡箍松动、破损和裂纹，制动软管连接器裂纹、砂眼，连接器密封圈老化、变形，制动软管接头裂纹和砂眼等，这些均属于不可测的失效模式且重要性不高。

笔者从某检修基地现场共收集到670条制动软管的寿命信息，并根据失效模式进行分类统计。失效总数为246条，除去过期的91条失效数据，得到总失效数据为155条，但各个失效模式之间存在交叉关系。其中，由于风水压泄露导致更换的软管有142条，占失效总数的91.6%；裂纹致使更换的软管有52条，占失效总数的33.5%；腐蚀 致使更换的软管有20条，占失效总数的12.9%；焊点致使更换的软管有4条，占失效总数的2.5%。因此，笔者将重点针对制动软管破损和泄露这两种主要的失效模式展开分析。由于受检修周期的限制，寿命信息属于删失数据，其中区间删失数据占221条，右删失数据占449条。另外，由于调研的企业于2015年建厂，部分零部件在建厂前的检修数据无存档记录，故属于左截断数据。

2 可靠性建模分析

针对不完整数据类型的可靠性分析，现有方法主要包括非参数方法和参数方法两大类。其中，非参数方法简单易行，但在不完整数据情况下偏差较大，如Kaplan-meier估计法[11-12]。传统的参数方法仅考虑删失数据，如JMP软件采用的统计分析方法[13-14]。近年来，在极大似然估计方法框架下，同时考虑左截断、区间删失、右删失的方法取得了较大进展[15-16]。笔者分别采用基于非参数方法(方法一)、仅考虑删失的参数方法(方法二)、同时考虑删失、截断的参数方法(方法三)分别进行建模。

2.1 累积失效概率的非参数估计方法

将原始数据按年份进行整理后，得到用于计算累积失效概率非参数估计的原始数据分布，如图1所示。

图1 制动软管数据分布图

图1中左上角小矩形框内数值表示在区间起点处于健康状态的零部件数量，大矩形框中数值表示在时间区间内的失效个体数，右上角箭头指向数值表示在该区间内未失效，但后续状态未知的右删失个体数量。以第2年为例，494个零部件在第2年年初为健康状态，在(1,2]时间区间内有124个软管失效，有91个软管在检测时并未发现故障，但后续状态未知。根据图1可以得到制动软管累积失效概率非参数估计值，并可根据相应公式计算得到累积失效概率，如表1所示。

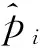
表1 制动软管累积失效概率非参数估计值

2.2 仅考虑删失数据的参数估计方法

参数估计方法的基本假设是寿命数据服从某一概率分布函数，故首先要进行寿命分布的选取。赤池信息准则(akaike information criterion，AIC)和贝叶斯信息准则(bayesian information criterion，BIC)常用于模型选择，是衡量统计模型拟合优良性的一种标准。模型中AIC、BIC值越小，则表明拟合效果越优。基于JMP软件对制动软管数据进行分布拟合，比较各寿命分布的AIC、BIC值，结果如表2所示。

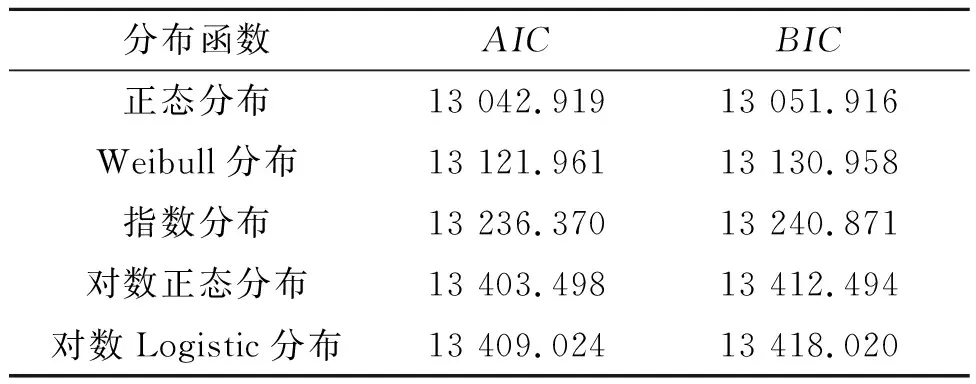
表2 不同分布模型的AIC、BIC值比较

由表2可以看出，正态分布的AIC值和BIC值均较小，是描述制动软管的最佳分布，故笔者以正态分布展开研究。在仅考虑删失数据的情况下，得到基于正态分布的累计失效概率与95%置信区间，如图2所示,可以看出服役时长1 500天时约有50%的零件失效。

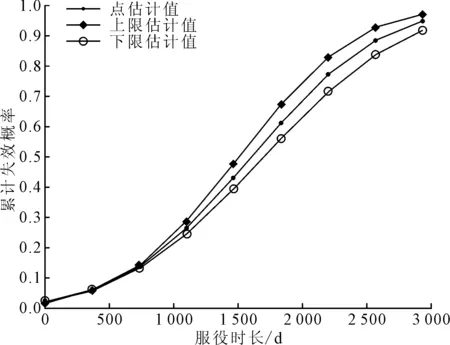
图2 基于方法二的累积失效函数图

2.3 同时考虑截断、删失数据的参数估计方法

通过对调研数据的拟合、评价，在制动软管服从正态分布的基础上，综合考虑制动软管实际检修过程中的截断、删失数据对评估结果的影响，通过求解似然函数得到参数估计值,如表3所示。

表3 基于方法三的参数模型估计值

制动软管寿命x服从截断正态分布x～N(1 525.221,829.4402),x>0。基于方法三的累积失效函数图如图3所示，可以看出制动软管服役至第5年时累积失效概率高达46.87%。

图3 基于方法三的累积失效函数图

笔者针对制动软管寿命数据不完整、不精确的特点，采用不考虑截断、删失的非参数估计、仅考虑删失数据的参数估计、同时考虑截断、删失的参数估计3种方法分别对拟合的累积失效函数进行了分析计算。非参数估计在制动软管服役第5年时累积失效概率达27.45%；仅考虑删失数据的参数估计在制动软管服役第5年时累积失效概率达43.41%；同时考虑截断、删失的参数估计在制动软管服役第5年时累计失效概率达46.87%，三者存在较大差异。由相关文献可知，同时考虑截断、删失的参数估计方法在理论上较优，但严谨起见，笔者针对不同方法进行了详细的比较和模型验证工作。

3 模型比较与验证

3.1 基于文献数据的对比分析

文献[15]中提供了含有左截断、右删失的服从Weibull分布的寿命数据，并证实了考虑截断、删失的极大似然估计法可以较为精确地进行参数估计。为了进一步进行验证，基于此数据，采用方法一、方法三进行了复刻，得到可靠度函数拟合对比，如图4所示。

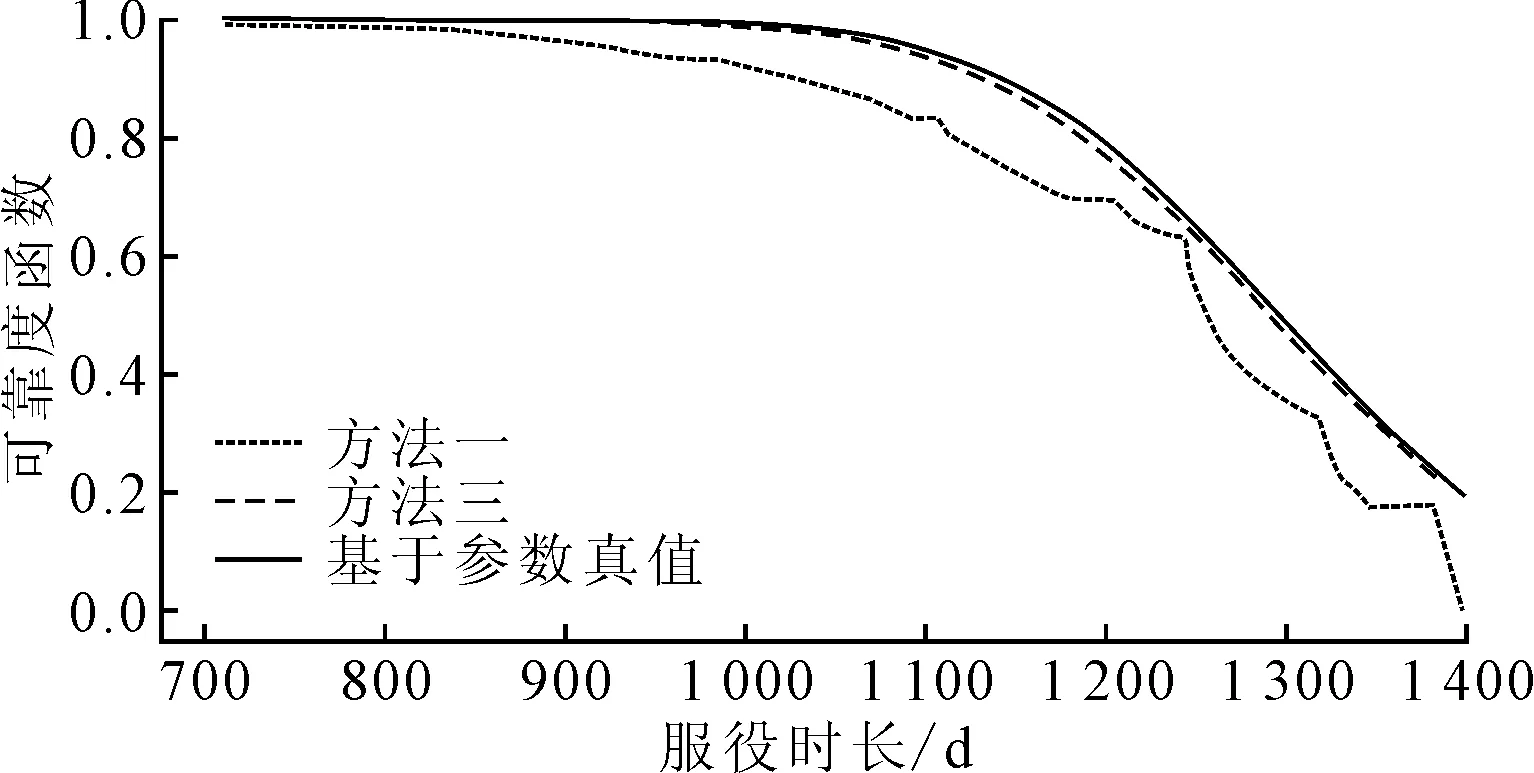
图4 基于文献数据集的可靠性函数拟合对比

由图4可看出，考虑删失、截断的参数估计法(方法三)与基于参数真值的可靠性函数基本吻合，而基于非参数方法(方法一)与真值偏差较大。可见在不完整数据下，非参数方法没有考虑删失、截断的影响，局限性较大，结果不够准确。由于制动软管的寿命数据更为复杂，不仅含有左截断、右删失，还含有区间删失情况，并且服从的分布函数与本节中的数据也有差别，因此需要进一步进行分析验证。

3.2 基于仿真的模型对比分析

由于制动软管的寿命分布参数真值不可得，因此采用蒙特卡洛仿真的方法进行分析验证。基于均值为1 525、标准差为830的正态分布生成1 000条仿真数据，对其中的2/3数据进行区间删失处理，对其中的1/3数据进行右删失处理，对30%的数据进行左截断处理，最终生成含有删失、截断的正态寿命数据，尽可能地复刻本研究中的实际数据集，然后根据3种方法对数据进行拟合，得到可靠性函数对比图，如图5所示。

由图5可以看出，基于2 000组蒙特卡洛仿真结果中，方法三的拟合效果最好，方法二次之，方法一的拟合效果欠佳。为进一步进行定量分析，将基于3种方法的拟合数据与仿真数据进行拟合曲线间面积的对比，结果如表4所示，差异面积越小，说明曲线间距离越近，拟合效果就越好。由表4可知，方法三的拟合效果最好，再次验证了以上结论。

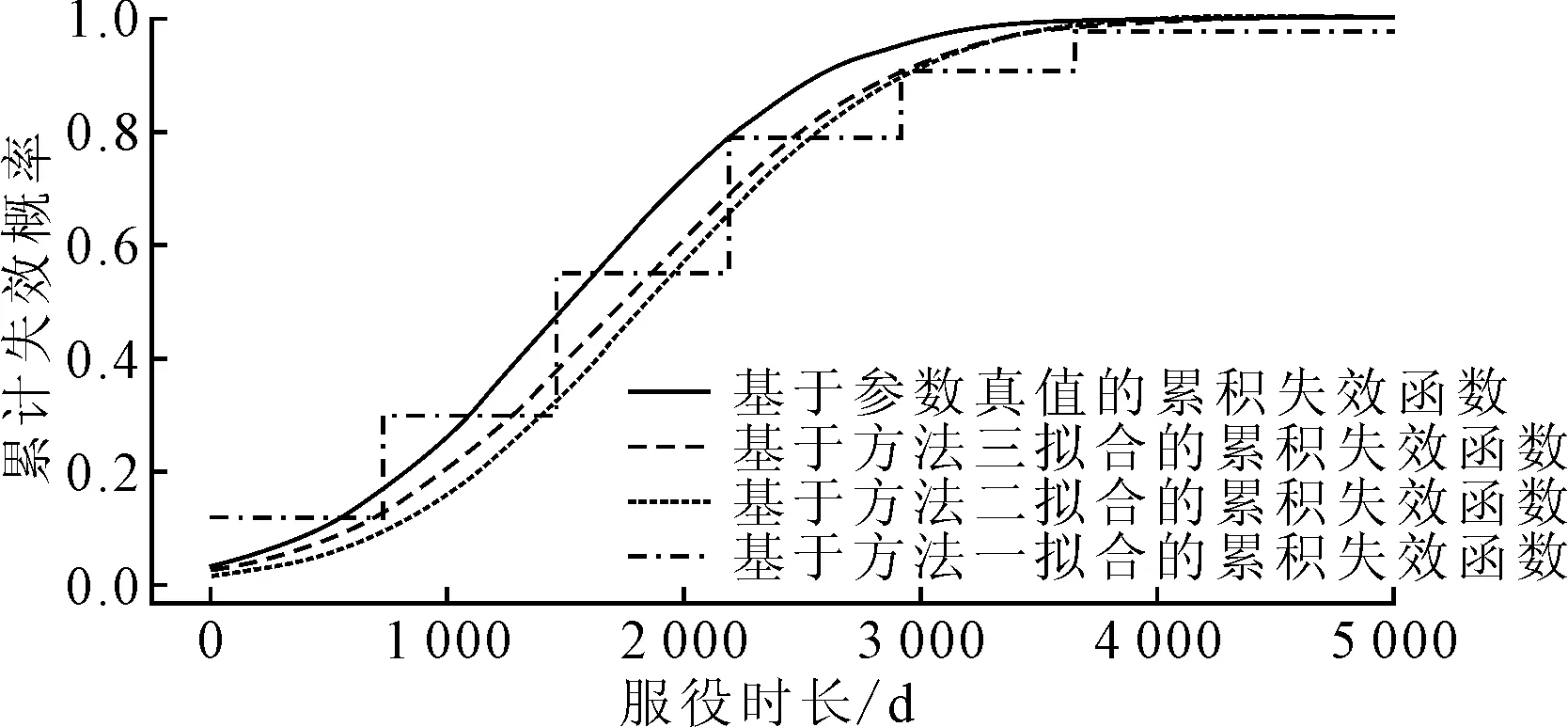
图5 基于仿真数据集的累计失效函数拟合对比

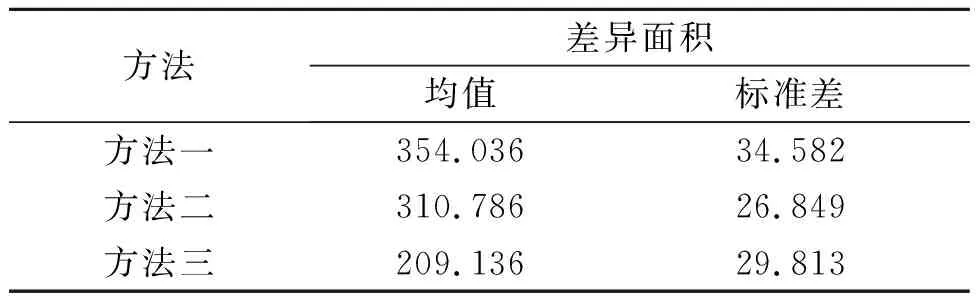
表4 3种方法的累计失效函数差异分析

3.3 基于交叉检验的模型验证

上文已证明了方法三的优越性，但由于缺少验证数据集，还需要对模型的外推精度进行验证。笔者采用K折交叉验证方法来验证上述数学模型的鲁棒性。将现有数据分割成K=3个子样本，其中1个子样本被保留为验证集，其他2个样本当作训练集。重复交叉验证3次，计算3次的平均值，最终得到一个单一估测。例如，设置1#样本数据作为验证集，则2#和3#样本数据为训练集。在3次验证中，训练集和验证集的参数值均比较近似。交叉验证的参数数值求解结果及置信区间如表5所示，可以看出参数的置信区间基本重合，且参数的点估计位于所有的置信区间内，证明了上述数学模型中失效规律的稳健性。

表5 制动软管K折交叉验证数据集参数估计值

4 模型应用

上述可靠性分析结果，可以广泛应用于零部件的维护维修和健康管理中。累计失效概率表征零部件整体寿命分布情况，对制定报废周期至关重要；条件失效概率表征零部件在服役中的寿命变化，可指导动态物料管理。因此，笔者将进行基于成本优化的制动软管报废周期优化和基于失效区间的制动软管物料管理研究。条件失效概率计算公式为：

(1)

制动软管部分条件失效概率的计算结果如表6所示，其中T0表示制动软管的当前役龄，τ表示制动软管再继续使用的时长，表中数据为该零部件在当前役龄下继续使用时长的条件失效概率。如表中0.240 5表示已使用2年的制动软管在未来2年的累积失效概率为0.240 5。

表6 制动软管部分条件失效概率参数估计值

4.1 基于成本优化的制动软管报废周期优化

定义制动软管的更换成本为CR，检修成本为CI，考虑到制动软管在使用过程中随着服役时间的增加，其期望剩余使用寿命会减少，故采用平均折旧的思想对个体的剩余价值进行估价。

(2)

式中：Gx为未来失效的概率值，为了便于说明，取中位数，即Gx=0.5；F(xt)为期望的累积失效概率；F(xs)为实际的累积失效概率。 以100个制动软管为例进行说明，由图3可看出，当制动软管使用至730天时，累积失效概率为0.080 9%，可以理解为100个个体中有0.08个失效，99.92个尚未失效。通过式(2)可计算出期望的累计失效概率为0.054，将结果代入方法三求得软管相对应的寿命时间，该结果减去已运行的天数(730 d)，得到此时尚未失效的制动软管的剩余期望运行时间为879 d，通过期望时间比值即剩余期望寿命/平均寿命(1 525 d)得到此时单个尚未失效制动软管的剩余价值为0.576CR，假设对制动软管进行全部检修，则耗费成本C1=100CI；其中尚未失效个体的剩余价值为C2=99.92×0.576CR=57.55CR，定义第一次全面维修经济判定指标ΔC1=C1-C2，若ΔC1≥0，表明第一次全面检修不经济，则不进行检修，直接进行更换；若ΔC1<0，表明第一次全面检修经济，则进行检修，对于检修失效的软管进行更换，未失效的继续使用。制动软管的寿命为6年，现有的检修制度为每2年进行1次检修，共有3次检修机会。制动软管检修成本算例中的相关参数与结果如表7所示。

表7 制动软管检修成本算例

由表7可知，设置制动软管更换成本CR为300元，检修成本CI为50元，当制动软管使用6年时，检修成本大于制动软管尚未失效个体的剩余价值，则此时不做检修，全部更换更经济，在此情境下可建议制动软管的报废周期为6年。由于制动软管购买成本和检修成本对模型结果具有一定的影响，后期如果购买成本和检修成本发生变化，可依据此模型进行更新计算。

4.2 基于失效区间的制动软管物料管理

笔者从现场共收集670条制动软管的寿命信息，其中有424件制动软管尚未失效，对其中30件制动软管的出现故障时间(即剩余使用寿命)进行预测，结果如图6所示。横坐标为经过对数转换后的制动软管服役时长，虚线展现的是在90%置信区间内零部件未来失效的时间估计，虚线左节点表示未来失效时间的区间下限，虚线右节点表示未来失效时间的区间上限。

基于个体出现裂纹时间的预测结果，可结合式(1)对未失效的424件制动软管未来1年内累积失效数量进行预测，结果如图7所示。由图7可知，该批仍未失效的制动软管自观测结束后的1年内累积失效79件，约为现存总体的18.6%，该结果可用于指导物资部开展物料采购。

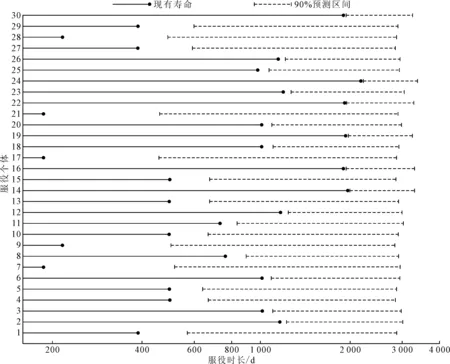
图6 个体出现裂纹时间90%预测区间

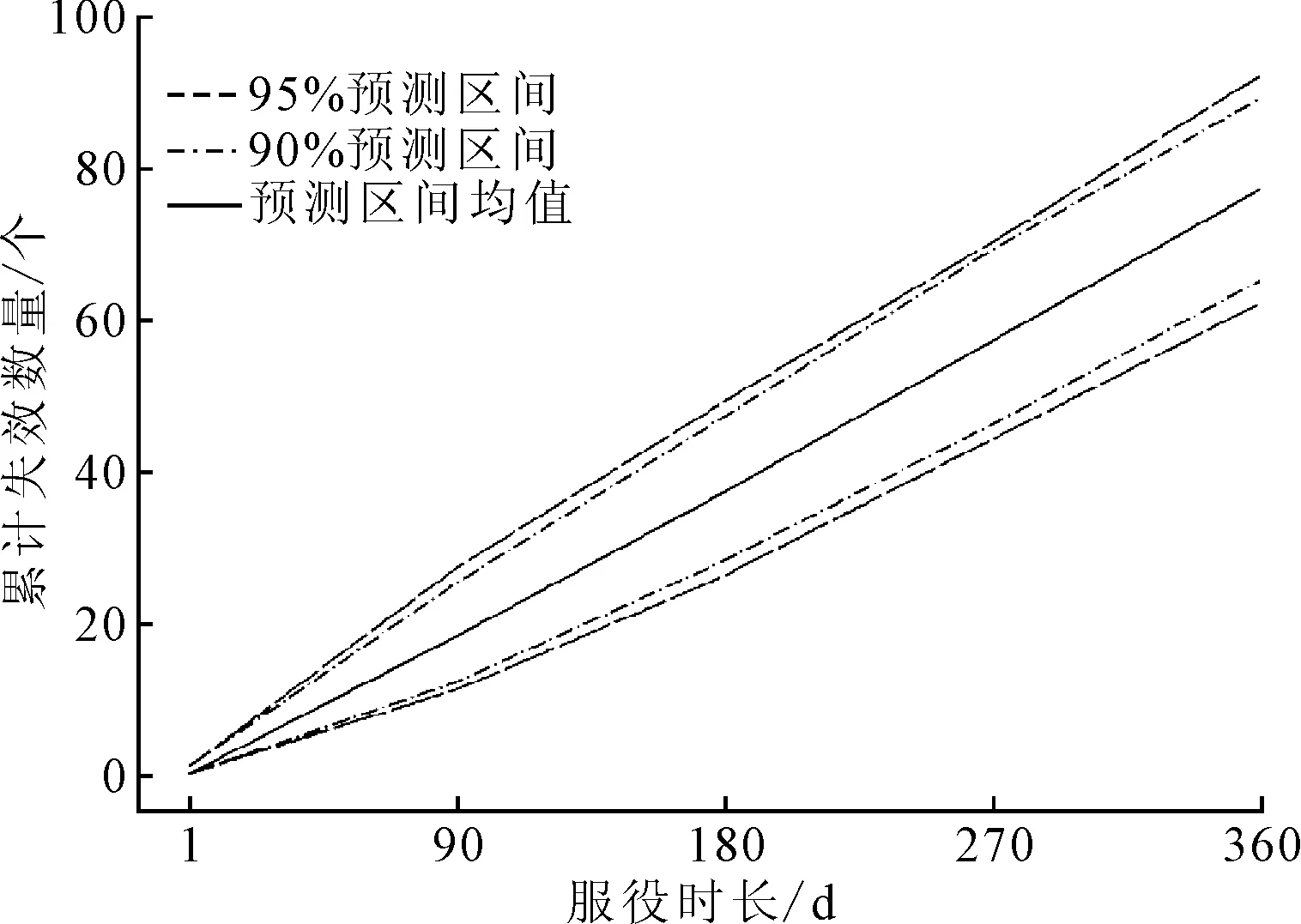
图7 现役个体1年累计失效数量预测

5 结论

(1)针对不完整寿命数据下的制动软管展开可靠性分析，通过同时考虑截断、删失的极大似然参数估计方法计算失效概率，完成了参数的点估计与区间估计，进而得到制动软管剩余寿命的区间估计。最后，基于可靠性分析结果进行了应用，包括基于成本优化的制动软管报废周期优化和基于失效区间的制动软管物料管理。

(2)深入分析了同时考虑截断、删失的极大似然参数估计方法相较于非参数方法和仅考虑删失数据的参数估计方法的优越性。非参数方法将失效数据进行一系列统计得到失效概率，在估计参数时未考虑数据的截断和区间删失，导致失效概率偏小。仅考虑删失数据的参数估计方法，无法解决“幸存者偏差”问题，在删失比例较大的情况下，参数估计不够精确。同时考虑截断、删失的极大似然参数估计方法能充分考虑数据的截断、删失情况，保证评估结果的准确性。文献数据对比和仿真数据分析均表明，同时考虑截断、删失的极大似然参数估计方法更加贴近参数真值。该研究也为复杂不完整寿命数据下的零部件可靠性分析及应用提供了技术路线和参考方法。

(3)笔者针对不完整寿命数据下的制动软管可靠性评估与应用问题展开研究，结合工程限制得到了一些成果，但还存在诸多不足，未来拟从以下3个方面进行改进。①现有的检修流程保证了制动软管的可靠性，但是会造成检修成本偏高，可展开制动软管检修流程优化研究等工作，以达到兼顾安全性和经济性的要求。②可展开检修策略优化研究，进一步推进基于状态的铁路货车维护维修模式。③可考虑零部件发生的各类失效模式，综合评判其运行状态。