含窄带噪声和白噪声的复杂染噪局部放电信号提取及应用

孙 抗，李万建，张 静

(1. 河南理工大学电气工程与自动化学院 河南 焦作 454000；2. 国网河南省电力公司商丘供电公司 河南 商丘 476000)

局部放电(以下简称局放)作为高压电气设备绝缘性能退化的主要表征形式，局放监测是评估电气设备在线运行状态的主要技术手段[1-4]。然而，局放信号十分微弱，且容易被运行环境中多种较高水平的噪声严重干扰甚至淹没，难以实现高完备度的提取，进而影响后续的局放定位精度[5-6]以及模式识别准确率[7-8]。

在实际运行条件下，局放信号中通常含有白噪声、周期性脉冲干扰和周期性窄带干扰这3 类噪声干扰[9]。其中，周期性脉冲干扰具有很强的规律性，容易滤除。白噪声的频带分布较广，可能在各个频段上与局放信号重叠；周期性窄带干扰由于常见且强度较大，针对这两类噪声的局放信号去噪是当前的研究重点和难点。

近年来，国内外学者针对局放信号去噪做了较深入的研究。文献[10]将广义S 变换与奇异值分解相结合，对局放信号中的白噪声进行抑制，但算法复杂度高，难以满足在线监测应用需求；文献[11]利用快速独立分量分析法(FastICA)对局放信号中的窄带干扰进行抑制，但去噪后信号的幅值和相位无法确定；文献[12]利用量子粒子群改进基于稀疏分解的去噪算法，但该算法必须事先构建过完备原子库；文献[13]采用紧支性准则选择小波基，克服了传统小波去噪算法中小波基选择的盲目性，但没有考虑到分解层数的问题；文献[14]利用经验模态分解方法实现局部放电去噪，算法的自适应性虽得到了验证，但其模态混叠以及端点效应等对去噪效果的影响不可忽略。

针对现有方法的缺陷，本文提出一种基于自适应噪声集合经验模态分解[15]结合小波包的染噪局放信号提取算法，能够在在复杂噪声环境下，无需先验数据，实现快速自适应的局放信号去噪。首先，利用CEEMDAN 对染噪信号进行自适应分解，并通过SVD 分解对分量中的窄带干扰及频率混叠进行抑制；然后，以信号间的互相关系数为准则判别有效分量并进行重构；最后，利用小波包阈值法滤除重构信号中残留的白噪声。实验结果表明，本文方法提取的局放信号波形畸变小、能量损失小，能够满足后续局放定位及模式识别等工作的需求。

1 自适应噪声的完全集合经验模态分解

1.1 自适应噪声的完全集合经验模态分解原理

针对经验模态分解(empirical mode decom position, EMD)存在的频率混叠、虚假分量以及端点效应的问题，文献[16]提出了集合经验模态分解(EEMD)，EEMD 算法在信号中添加一定强度的白噪声后对其进行EMD 分解，重复n次，通过求解各固有模态分量(IMF)的n次平均值确定最终的分量，但残留的白噪声使得重构信号与原信号相比有较大的误差；文献[17]提出了一种完全经验模态分解(CEEMD)，通过成对的加入正负噪声来减少EEMD 重构信号中残存的白噪声，但分解过程中计算量较大且重构信号的完备性较差。CEEMDAN算法以EMD 为基础，在原始列中自适应的加入白噪声，既解决了EEMD 加入噪声后分解模态个数不确定的问题，又减少了分解过程中的计算量，且可以得到完整度较高的重构信号。

1.2 CEEMDAN 有效分量拾取

CEEMDAN 算法去噪的关键在于分解后对有效分量的拾取。在当前研究中，主要依靠自相关系数[18]、能量门限[19]、峭度值[20]等作为有效分量的判别依据，但当分量中含有较多的窄带干扰信号时，上述方法可能会丢失部分有效分量，对去噪效果造成不良影响。

根据奇异值分解(SVD)理论可知，在分解得到的非零奇异值中，前q个较大的奇异值对应有效成分，其余的奇异值则被认为对应冗余成分。因此，可选取前q个奇异值对应的分量进行重构，从而实现信号的提纯。研究发现，局放信号在常见的高斯白噪声与窄带噪声的干扰下，对应的奇异值特征具有明显的差异，如图1 所示。

通过观察可知，3 组信号奇异值特征曲线中后段变化趋势基本相同，其中含有白噪声的局放信号相对于原始局放信号仅在幅值上略微增加。而含有窄带噪声的局放信号则在前几个奇异值处出现幅值突然增大的现象。根据此特点，可利用奇异值分解抑制CEEMDAN 分解得到的窄带干扰分量。

为了对IMFk进行SVD 分解，首先对各个分量构造Hankel 矩阵[21]。

在有效分量的拾取中，采用互相关系数法。互相关系数法在信号处理领域用来表示两个信号之间的相似性度量，通过已知信号来发现未知信号的特征[18]。通常情况下局放信号和噪声的相关系数非常小，但当IMF 中局放信号含量较高、噪声水平较低时，对应的互相关系数较大；相应地，IMF 中放信号含量较低、噪声水平较高时，互相关系数较小，且互相关系数与信号幅值无关。互相关系数计算公式如下：

2 自适应小波包阈值法

对上述有效分量进行重构后，信号中仍含有少量的白噪声，采用改进的小波包阈值法对白噪声进行抑制。如何提高阈值函数及阈值对噪声大小的自适应性，进而提高去噪后波形的拟合程度，是影响去噪效果的关键一步。文献[22]提出的阈值函数的广泛应用证明了小波阈值法去噪的优越性，但传统硬阈值函数的非连续性、软阈值函数的恒定误差会使去噪后波形发生较大畸变。随着相关研究的深入，更多的改进阈值函数被提出，有代表性的3 种改进阈值函数[23-24]分别如式(11)～(13)所示：

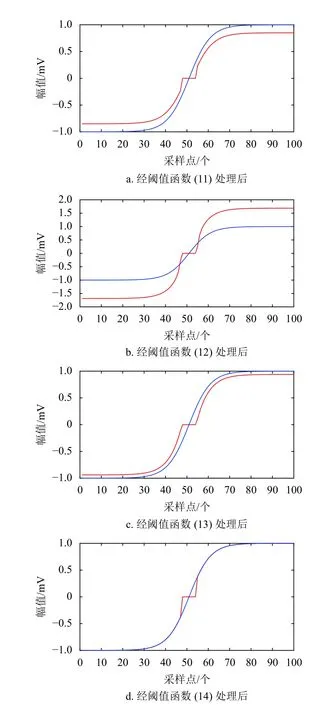
图2 不同阈值函数拟合结果对比

从上图可以明显看出，图2b 的拟合程度最差，图2a 和图2c 次之，图2d 的拟合程度最好，基本上消除了偏差。这表明本文提出的阈值函数较之其他3 种改进的阈值函数可以更有效地消除含噪信号小波系数与估计小波系数的恒定偏差。

3 基于CEEMDAN 结合小波包的去噪方法

综上所述，本文提出一种基于CEEMDAN 结合小波包的复杂染噪局放信号提取方法，步骤如下。

1)将染噪局放信号进行CEEMDAN 自适应分解，得到N个IMF。

2)构造各IMF 对应的Hankel 矩阵，对其进行SVD 分解，将奇异值不连续的点置零后进行信号重构。

3)计算各个固有模态分量与原始信号的互相关系数，提取其中有效IMF。

4)将各有效IMF 进行合成，利用改进的小波包阈值法对合成信号中的残留白噪声进行抑制。

详细流程如图3 所示。

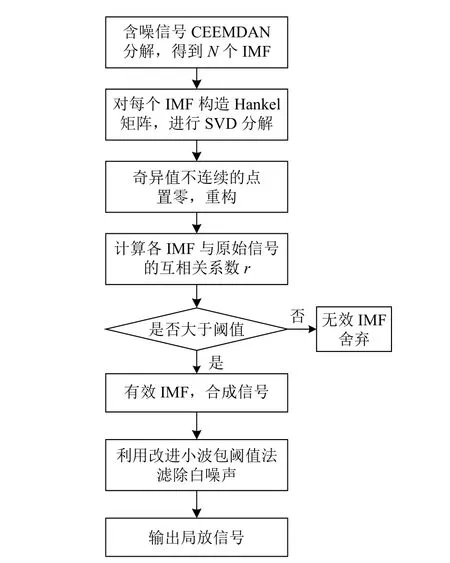
图3 算法流程

4 仿真实验及结果分析

4.1 复杂染噪局放信号生成

文献以及现场实验证明，不同类型电气设备局部放电信号可由如下两种数学模型表达[25]。

在仿真实验中，采用归一化幅值的单指数振荡衰减模型与双指数振荡衰减模型模拟局放信号。设置采样频率为20 MHz，衰减系数分别为2 μm、1.3 μm，采样时长为200 μm，振荡频率为1.2 MHz，如图4a 所示。在生成的局放信号中添加白噪声与窄带干扰模拟现场环境噪声，白噪声采用均值为0，方差为0.3 分布的高斯白噪声；根据现场测量经验，窄带干扰采用频率分别为100 KHz、500 KHz、1.2 MHz、5 MHz、7 MHz 的叠加正弦信号模拟。含噪局放信号如图4b 所示，经计算，上述设置含噪信号的信噪比为-6.5 dB。

图4 局放信号仿真波形

4.2 去噪实验及结果分析

利用本文方法对含噪局部放电信号进行去噪，在CEEMDAN 分解中，设置白噪声强度为0.2，循环次数为100 次[26]。经CEEMDAN 分解后的各个固有模态分量及其频谱如图5 所示。

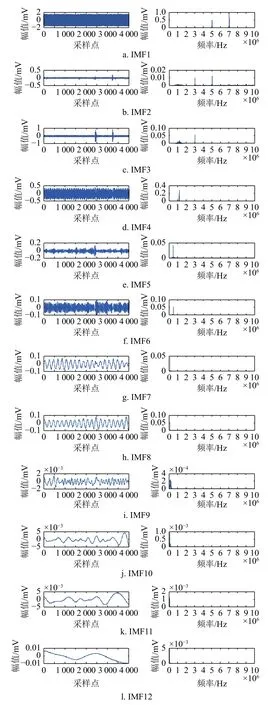
图5 染噪信号固有模态分量及其频谱

由各个固有模态分量的时域图可直观确定IMF2、IMF3 为有效分量，但仅对这两个分量进行合成必定会损失原始信号能量。本文通过计算各个固有模态分量与原始信号的互相关系数，如表1所示，以进一步对有效分量进行拾取。

表1 各固有模态分量与原始信号的相关系数

通过分析多组实验数据可知，当互相关系数大于0.001 时，可认为该固有模态分量为有效分量。分别对IMF1、IMF2、IMF3、IMF4、IMF5、IMF6、IMF7、IMF9 进行Hankel-SVD 计算，波形变化如图6 所示，左图为有效分量，右图为经Hankel-SVD处理后的有效分量。

图6 Hankel-SVD 计算前后波形频谱对比

观察图6 可知，有效分量中的窄带干扰已经明显得到了抑制，但各分量中仍存在大量白噪声。本文选择db10 小波基，结合前述阈值函数对合成分量进行小波包阈值去噪，得到波形如图7a 所示。为了验证方法的有效性，利用CEEMD降噪方法[27]和VMD 小波阈值法[28]的处理结果进行对比。基于CEEMD 的方法首先对信号进行CEEMD 分解，通过峭度值对分量中的虚假分量进行滤除，之后对有效分量合成，再利用小波阈值法进一步去噪。VMD 小波阈值法首先选择合适的分解层数对信号进行VMD 分解，利用相似系数选择有效分量后进行阈值降噪，将降噪后的分量合成后进一步利用小波阈值去噪。这两种方法的去噪结果如图7b、图7c 所示。

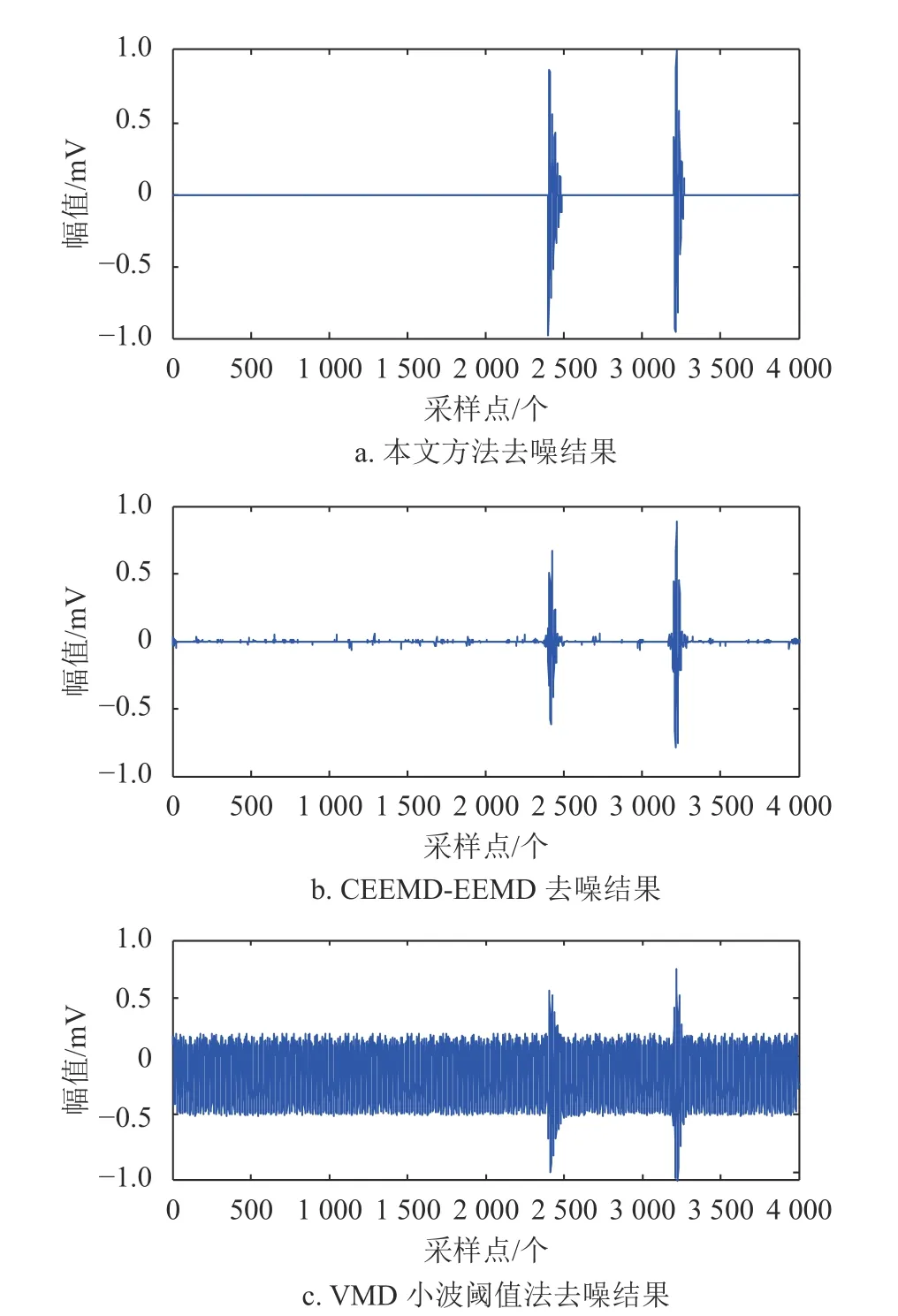
图7 不同方法去噪结果对比

为了定量对比去噪效果，引入信噪比(signal noise ratio, SNR)、波形相似系数(normalized correlation coefficient, NCC)、变 换 趋 势 参 数(variation trend parameter)、幅值相对误差4 个参量作为评价指标[29]。其中，SNR 越大表示算法的噪声抑制能力越强；NCC 用于评价去噪后信号与理想局放信号的波形相似度，其值越接近1，代表波形相似度越高；VTP 表示去噪前后波形变化趋势的相似程度，越接近1，表示两种波形的变化趋势越相似；幅值相对误差则体现了去噪过程中信号的能量损失程度。分别计算上述3 种去噪方法的评价指标，结果如表2 所示。

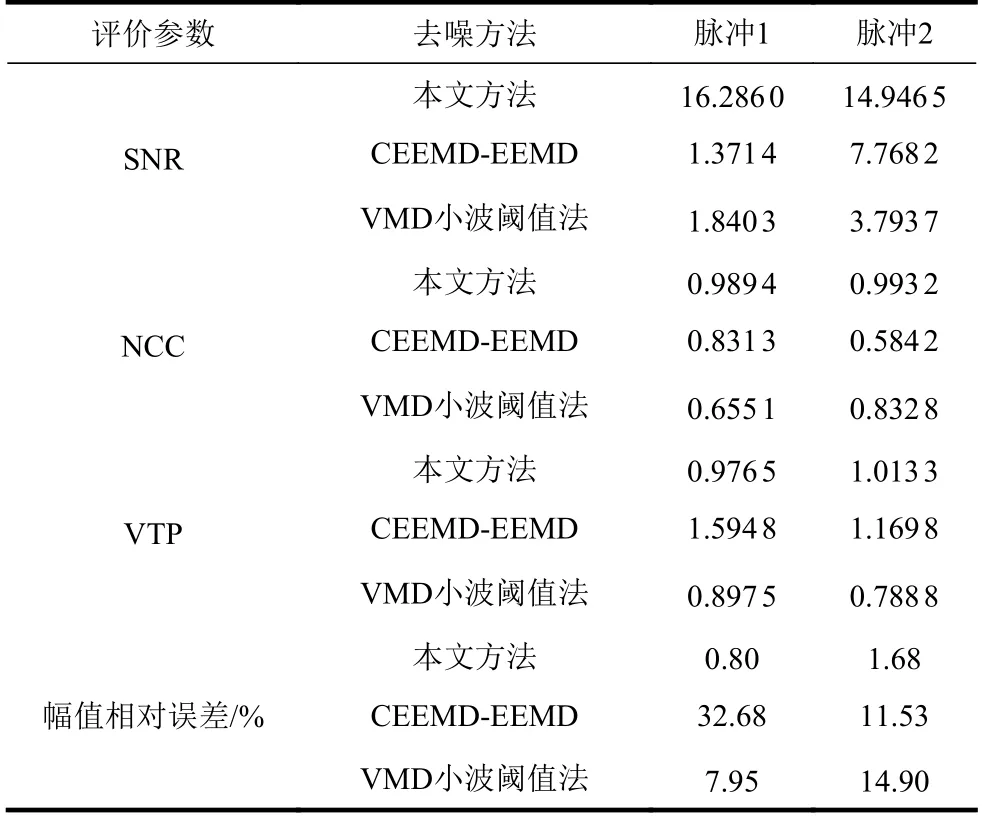
表2 各方法去噪效果评价参数

根据对比图7 及表2 所示的去噪结果和定量指标，可以得出以下结论。

1) 本文所提出的基于CEEMDAN-Hankel-SVD的局放信号去噪方法，去噪后信噪比高，波形未发生大幅度畸变，能量损失最小。

2) 基于CEEMD 的去噪方法对信号进行两次阈值处理，虽然噪声得到了良好的抑制，但去噪过程中的能量损失过大。

3) VMD 小波阈值法由于窄带干扰与局放信号的振荡频率一致，使其无法有效滤除，从而导致算法失效。

图8 为本文方法对两种局放脉冲信号去噪前后的波形叠加对比图。由图可直观发现，本文所述基于CEEMDAN-Hankel-SVD 的去噪算法，对局放信号中的窄带干扰与白噪声有着良好的抑制效果，能最大限度的还原局放脉冲信号，且波形畸变小。

图8 去噪前后波形对比图

5 实测局放信号去噪应用

为了进一步验证算法的实用性，将其应用于电力电缆局部放电的在线定位。在基于高频电流传感器(HFCT)的定位方法中，脉冲到达时间是保证局放定位精度的关键，实验采用时变峰度法提取局放脉冲到达时间。局放信号实验采集平台如图9 所示，局放信号通过将HFCT 套在电缆接地铜线上检测，示波器采样频率为100 MHz，得到局部放电波形如图10a 所示。

图9 电力电缆局放信号采集装置

由于实验室中噪声水平较低，局放信号波形较为明显，进一步添加与第4 节实验同等水平的窄带干扰与白噪声，提高干扰强度，得到的染噪局放信号如图10b 所示。为了便于后续处理，将测量到的信号幅度归一化，采用本文算法的去噪结果如图10c 所示。利用时变峰度法拾取重建信号的局放脉冲到达时间，其时变峰度曲线如图10d所示，算法拾取结果与手动拾取结果一致，皆为第262 个采样点，验证了去噪算法的有效性。

图10 局部放电脉冲提取及拾取结果

6 结 束 语

1)本文采用的Hankel-SVD 算法可有效抑制CEEMDAN 固有模态分量中的频率混叠与窄带干扰，以此为基础的局放信号提取方法能够最大程度的还原原始信号。

2)本文改进了阈值函数及阈值计算方法，阈值函数结合了软、硬阈值的优点，算得的阈值大小适中，既保留了信号的连续性，又减小了恒定误差。

3)本文方法可有效去除白噪声和窄带噪声干扰，提取的局放信号波形畸变小、能量损失小，能够满足后续的局放定位等应用需求。