CSP 焊点焊后残余应力分析与预测
2021-01-22黄春跃赵胜军唐香琼
黄春跃,赵胜军,梁 颖,匡 兵,唐香琼
(1. 桂林电子科技大学机电工程学院 桂林 541004;2. 成都航空职业技术学院电子工程系 成都 610021)
电子产品的微型化、轻薄化、多功能化与高可靠性的发展趋势,使得高密度和高精度的封装技术成为热点。芯片尺寸封装(chip scale package, CSP)作为一种新型的封装技术,具有体积小和封装密度高等优点[1]。CSP 封装器件在组装过程中,焊点材料会从固态变化到熔融状态,随焊接过程的进行而又冷却凝固到固体状态,这一变化会使得焊点内会产残余应力,若残余应力过大,就会引起焊点的损伤,这种损伤会导致器件的失效[2],因此,对焊后残余应力所引起的焊点失效问题应该给予足够重视以确保焊点服役后的可靠性。国内外学者已开展了相关研究,文献[3]针对PCB 组装板级组件焊点焊后残余应力进行了研究,结果表明残余应力与封装体积有关;文献[4]分析了BGA 焊点结构参数对焊点焊后残余应力的影响,结果表明与PCB 同侧的焊盘直径和焊料量对残余应力影响显著;文献[5]对焊点残余应力研究的结果表明,芯片的厚度、焊点间距和焊点直径是影响残余应力的主要因素。以上研究表明,焊点形态参数的变化对残余应力影响显著,但也有一些地方研究不够充分,比如,没有具体给出对残余应力有显著影响的因素之间的影响程度大小的排序,残余应力的计算工作量大等问题尚未充分解决。灵敏度分析是解决多变量分析的方法,而BP(back propagation)神经网络能够实现多个变量之间非线性映射关系,且在焊点形态、故障诊断和焊接质量等领域被广泛应用[6-8]。因此,本文以CSP 无铅焊点为研究对象,首先建立了CSP 焊点有限元模型,并进行了残余应力分析;然后基于灵敏度分析对焊点结构参数进行了分析;最后选取焊点结构参数灵敏度显著的因子,基于带动量项BP 神经网络,建立了显著因子与残余应力之间的非线性映射关系,实现了对CSP 焊点焊后残余应力的预测,为进一步深入研究CSP 焊点焊后残余应力进而提高CSP 焊点服役后的可靠性提供了理论指导。
1 CSP 焊点焊后残余应力有限元分析
1.1 有限元分析模型
基于ANSYS 软件,根据实际的芯片,建立的CSP 焊点有限元仿真模型如图1 所示。
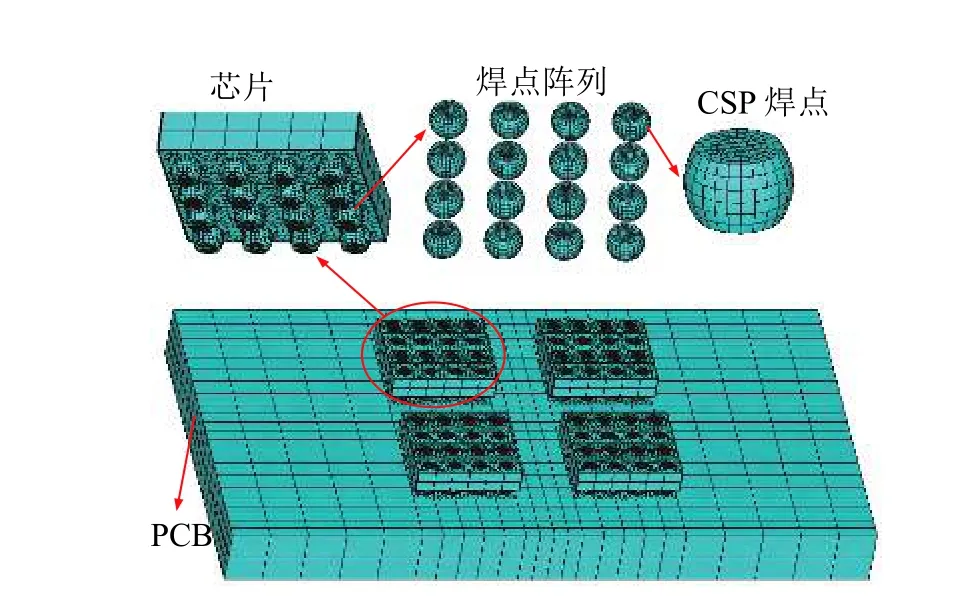
图1 CSP 焊点残余应力有限元分析模型
模型包括4 块美国仙童半导体公司生产型号为FAN48632UC33X 的CSP 芯片、CSP 焊点和PCB,芯片尺寸为1.63 mm×1.63 mm×0.4 mm;每个芯片都有16 个CSP 焊点,按照4×4 全阵列排列,材料选用SAC305 无铅焊料;焊点直径、高度和间距分别为0.25 mm、0.2 mm 和0.4 mm;焊盘直径为0.2 mm;PCB 尺寸为10 mm×6 mm×1 mm。由于焊点形态的复杂性,基于最小能量原理的surface软件对焊点形态进行模拟。为了仿真结果更加准确,网格划分时采用映射网格划分方法,并对焊点部分进行了细化,划分后模型中包含单元数81 966、节点数102 299。模型中的材料参数如表1所示。

表1 材料属性
1.2 CSP 焊点焊后残余应力分析
采用间接耦合分析方法对CSP 焊点进行再流焊焊后残余应力有限元分析。首先对模型的温度场分析,然后将温度场分析的结果作为载荷进行热结构耦合分析。热分析过程中采用Solid70 单元,边界条件为无铅再流焊温度曲线,如图2 所示,包括预热、保温、再流和冷却区域。图中a 点冷却凝固温度为187.2 °C,b 点和c 点所对应的温度为25 °C。
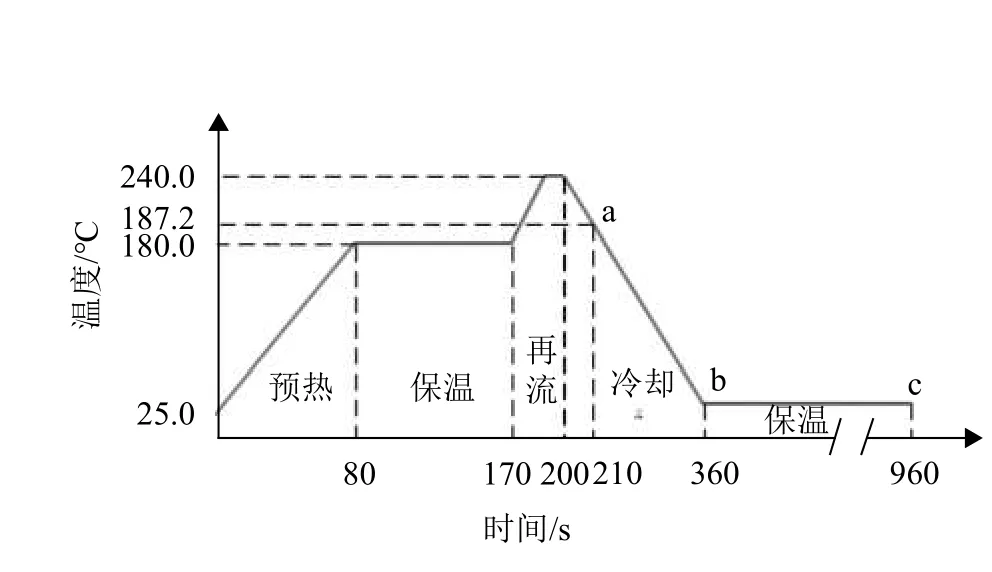
图2 再流焊温度加载曲线
对CSP 焊点模型进行残余应力分析过程中,设置焊点冷却凝固温度187.2 °C (图中a 点所对应时刻)作为模型初始温度,并将此时刻做为仿真分析的初始时刻;150 s 后冷却至b 点(360 s)时刻,再继续保温至c 点(960 s)时刻,该时刻为仿真分析结束时刻。结构分析过程中采用Solid185 单元,边界条件为模型中PCB 底面4 个角点位移全约束。对CSP 焊点焊后残余应力的仿真分析,所得应力应变结果如图3 和图4 所示。
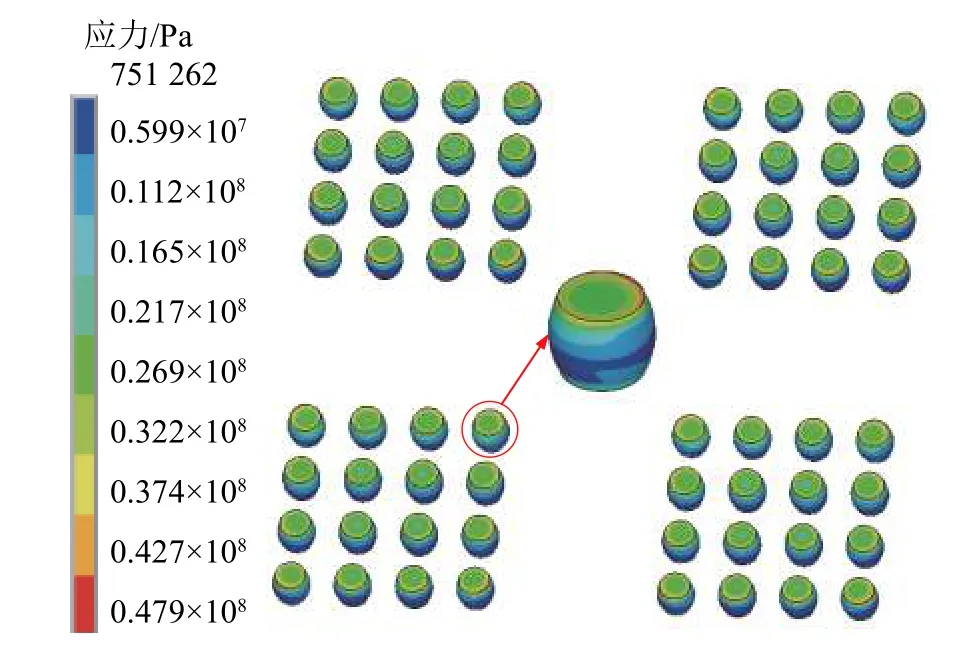
图3 CSP 焊点残余应力分布
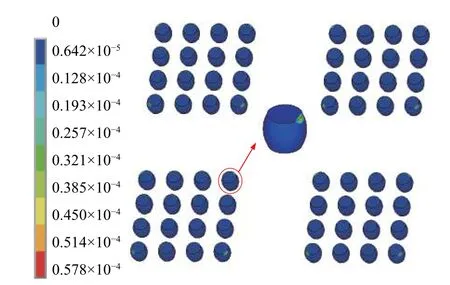
图4 CSP 焊点残余应变分布
由图3 可知,CSP 焊点焊后残余应力的分布不均匀;距离焊点阵列中心位置越远的焊点,最大残余应力越大;在单个焊点内残余应力的分布状态为,从上焊盘到下焊盘先减小后增大;最大残余应力值为47.898 MPa,位于焊点与芯片接触的区域,这是由于这3 种材料中芯片与焊点的热膨胀系数相差最大。由图4 中可知,残余应变分布不均匀,距离焊点阵列中心越远位置的焊点,残余应变越大,最大残余应变值为0.000 057 8。
2 CSP 焊点焊后残余应力灵敏度
为了研究焊点形态参数(焊点直径、焊点高度、焊盘直径和焊点间距)的变化对CSP 焊点焊后残余应力的影响,以及各参数灵敏度大小,本文对该模型进行了灵敏度分析。
2.1 灵敏度分析
灵敏度分析能够得到设计变量对输出变量的贡献率,能够分析各个参数对输出变量的影响程度,使得设计人员更能了解哪种设计变量的影响较大,哪种影响较小,以便更加关注敏感因素和剔除不敏感因素,减少设计过程中的盲目性。灵敏度分析包括局部和全局灵敏度分析,前者只能检验单个变量的变化对响应的影响程度;而后者可以检验多个设计变量的变化对响应的影响程度。本文中残余应力的大小受到了多个参数变化的共同作用,所以全局灵敏度分析的方法更为合适。因此,对CSP 焊点焊后残余应力的分析选用全局灵敏度分析方法,使得结果更加准确可信。
2.2 CSP 焊点焊后残余应力的灵敏度分析结果
在灵敏度分析过程中为了使CSP 焊点形态参数相互独立,互不干扰,本文采用ANSYS 软件PDS 模块的拉丁超立方蒙特卡罗模拟技术进行仿真分析。研究表明,蒙特卡罗法是目前可靠性分析结果准确性验证的唯一手段[9],只要建模准确,模拟次数足够多,所得结果就可以认为是可信的。灵敏度分析过程中,选用焊点高度(SB_H)、焊点直径(SB_D)、焊点间距(SB_DIST)和焊盘直径(SB_P1)作为输入参数,且分别服从上限值和下限值为SB_H(0.15, 0.25) mm、 SB_D(0.22, 0.28) mm、SB_DIST(0.32,0.4) mm 和SB_P(0.18,0.22) mm的均匀分布;选用最大残余应力(SMAX)作为输出参数。对CSP 焊点结构参数进行灵敏度分析后,所得输入参数的散点图和灵敏度图如图5 和图6所示。
从图5 中可知,焊点直径与最大残余应力成正相关关系;焊点间距与最大残余应力成正相关关系;焊盘直径与最大残余应力成负相关关系;焊点高度与最大残余应力成负相关关系。
由图6 可知,置信度为95%情况下,对CSP焊点最大残余应力SMAX 影响较为显著的因素有3 个,即为焊点直径、焊盘直径和焊点间距。按照灵敏度从大到小的顺序排序为:焊点直径>焊盘直径>焊点间距。焊盘直径与最大残余应力成负相关关系,焊点直径和焊点间距与最大残余应力成正相关关系。
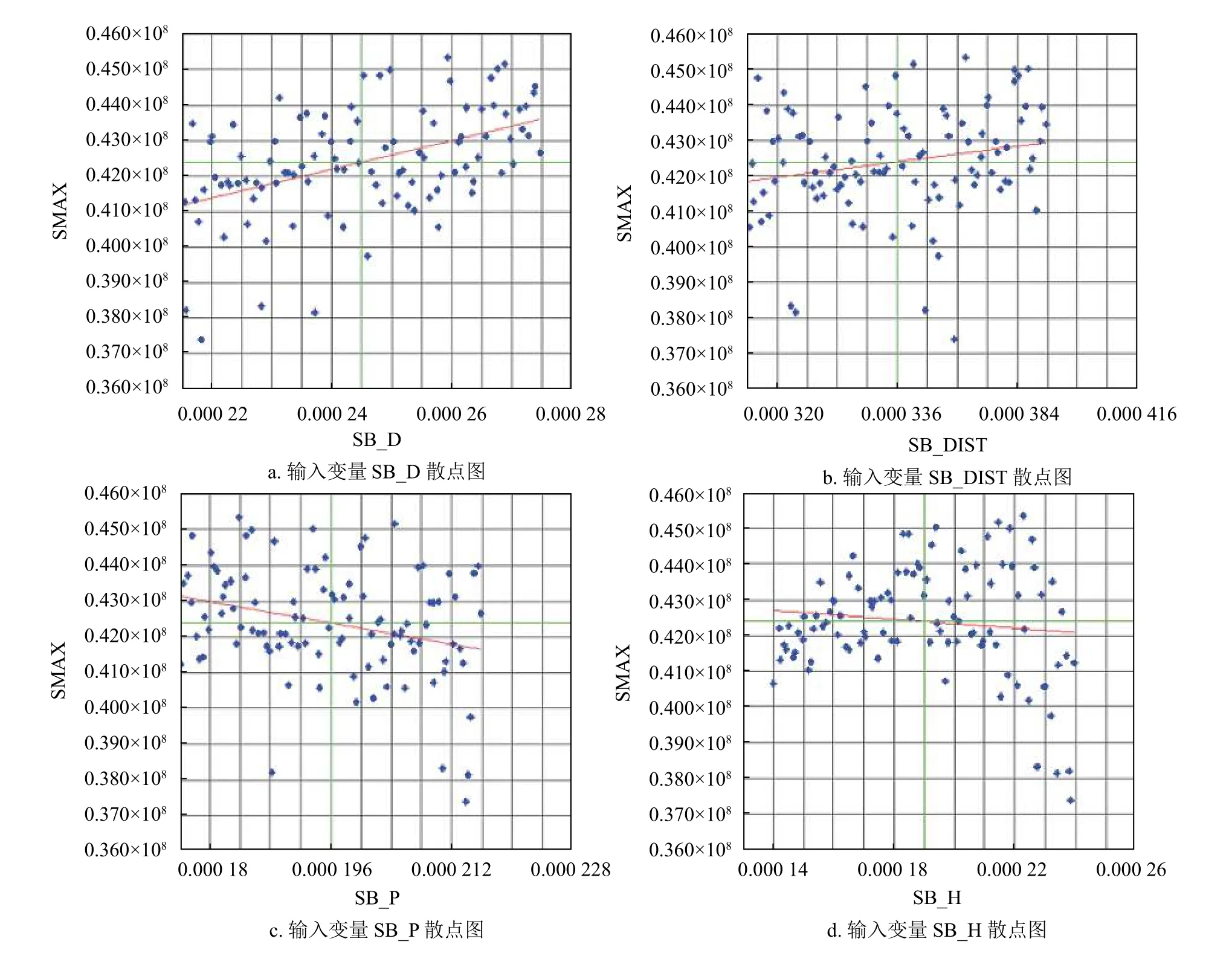
图5 输入参数的散点图
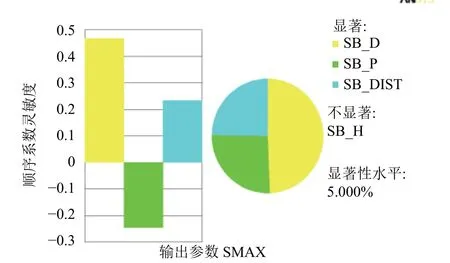
图6 灵敏度图
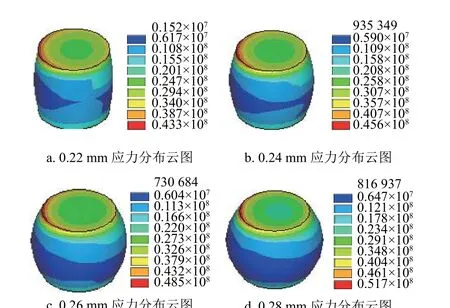
图7 不同CSP 焊点直径的残余应力云图
2.3 灵敏度分析结果有效性验证
为了进一步验证上节灵敏度分析的准确性,本文选取灵敏度分析结果中对残余应力影响最显著的因子(焊点直径)进行单因素分析。只改变焊点的直径,其他参数与初始模型参数保持一致,焊点直径取0.22 mm、0.24 mm、0.26 mm 和0.28 mm,建立相对应的4 个有限元模型并进行仿真分析,有限元分析结果如图7 和表2 所示。
图7 为4 种不同直径的CSP 焊点内的焊后残余应力分布云图,为便于相互比较,将最大焊后残余应力值列于表2 中。由图7 和表2 均可知,CSP 焊点内最大残余应力随焊点直径增大而增大,0.22 mm 所对应的最大残余应力为43.311 MPa,0.28 mm 所对应的最大残余应力增大为51.727 MPa;这一变化规律与灵敏度分析结果图5a 中所得规律一致,因此证明了本文灵敏度分析的有效性。

表2 焊点直径对残余应力影响
3 基于神经网络的残余应力预测
针对采用有限元仿真分析方法获得CSP 焊点焊后残余应力工作量大、计算周期长及要求硬件条件高等缺点,本文基于MATLAB 软件采用带动量项改进BP 神经网络算法,即带动量项BP 神经网络来预测CSP 焊点残余应力值[10-11]。
3.1 带动量项BP 神经网络
BP 神经网络是一种误差反向传播的前馈式网络。由于结构简单易掌握且能够实现快速输入到输出的非线性映射关系,因此在事物预测领域被广泛应用。标准BP 神经网络算法中学习率和稳定性存在着一定的矛盾,学习率较大时,网络的收敛快而网络不稳定;学习率较小时,网络相对稳定而收敛速度变慢。因此本文以带动量项BP 神经网络算法解决该问题,并对CSP 焊点焊后残余应力进行预测分析。增加动量项的方法是在误差反向传播过程中对权值进行修正,其公式为:
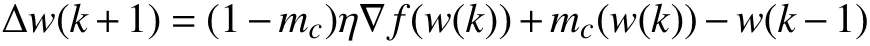
式中,w为权值;k为迭代次数;mc为动量因子,在[0,1]之间,一般取0.9 左右;η 为学习率;▽f(w(k))为误差函数梯度。阈值与权值修改公式相同。
3.2 残余应力预测模型
3.2.1 选择训练样本
根据本文灵敏度分析结果,选取对CSP 焊点焊后残余应力影响显著的焊点直径、焊盘直径和焊点间距这3 个因子做为带动量项BP 神经网络的输入,确定输入层节点数为3;以残余应力作为输出,确定输出层节点数为1;采用Kolmogorov定理确定隐含层节点数在[3, 12]之间,经多次试验,确定隐含层的节点数为9。
要实现带动量项BP 神经网络精确预测残余应力值,一定数量的训练样本尤其关键,各因素分布是否合理对最终预测效果有影响。所以,本文首先根据正交试验设计的原理,采用L16 (45)正交表获取了3 因素4 水平的16 组不同因素水平组合,然后以此为基础,把样本数据增加到了45组。以45 组不同的CSP 焊点形态参数组合与对应的残余应力值作为神经网络的训练样本,如表3所示。
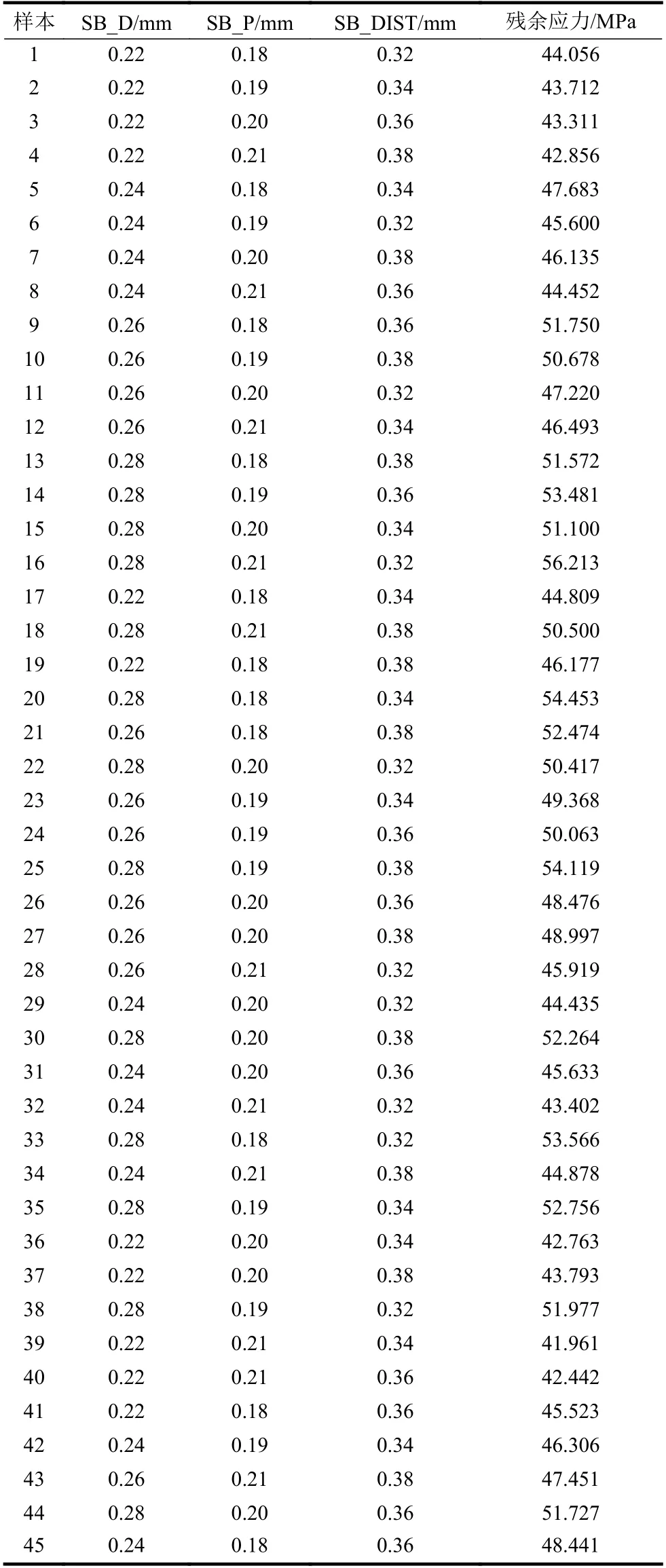
表3 训练样本数据
3.2.2 带动量项神经网络残余应力预测模型的实现
选择tansig 作为传递函数,学习率为0.05,最大迭代次数为3 000,根据带动量项的权值和阈值的修改方法,选取动量因子为0.8,编写带动量项的BP 神经网络程序,运行后所得全局误差减小,如图8 所示。误差在迭代训练第3 000 次时为0.035 15。为了分析训练后输出值和目标输出样本的相关性,对它们进行线性回归分析,其结果如图9 所示。
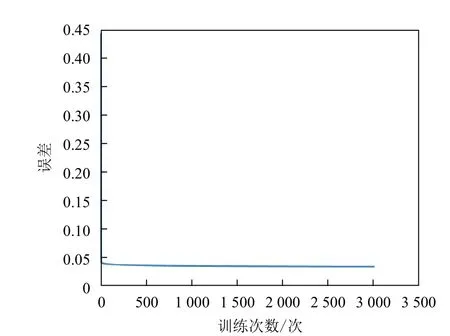
图8 带动量项BP 神经网络的全局误差
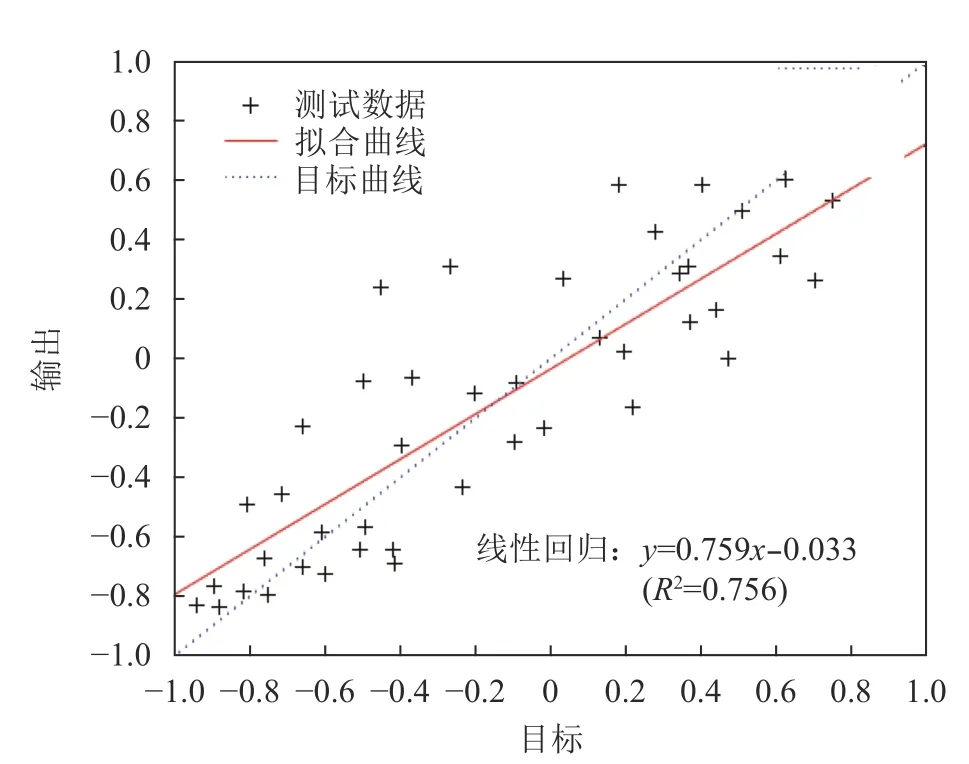
图9 带动量项BP 神经网络的线性回归分析
从图9 中可见,所得线性回归方程为y=0.759x-0.033,且带动量项的BP 神经网络经过训练后的输出值与期望输出值的线性回归分析中相关指数R2为0.756。当相关指数R2为0.75 时,就表明输出值与期望输出值有强相关关系,网络拟合效果较好。由此可见,带动量项的BP 网络残余应力预测模型的拟合效果较好。
3.3 残余应力预测模型的测试
为了测试已完成学习训练的带动量项BP 神经网络模型的预测效果,另取10 组测试样本数据对网络进行测试,样本数据与相应的预测值和仿真值对比结果如表4 与图10 所示。
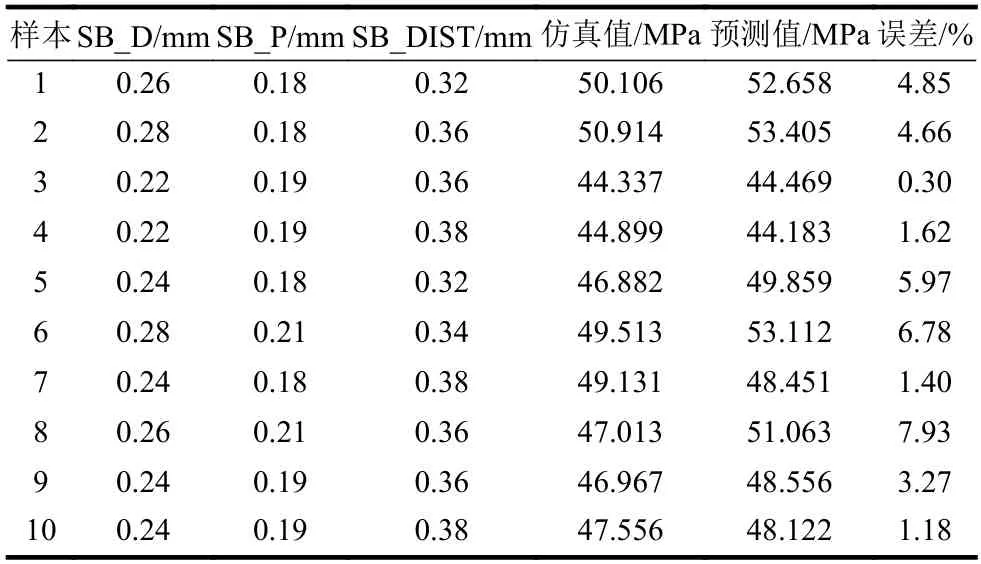
表4 带动量项BP 神经网络的预测值和仿真值对比
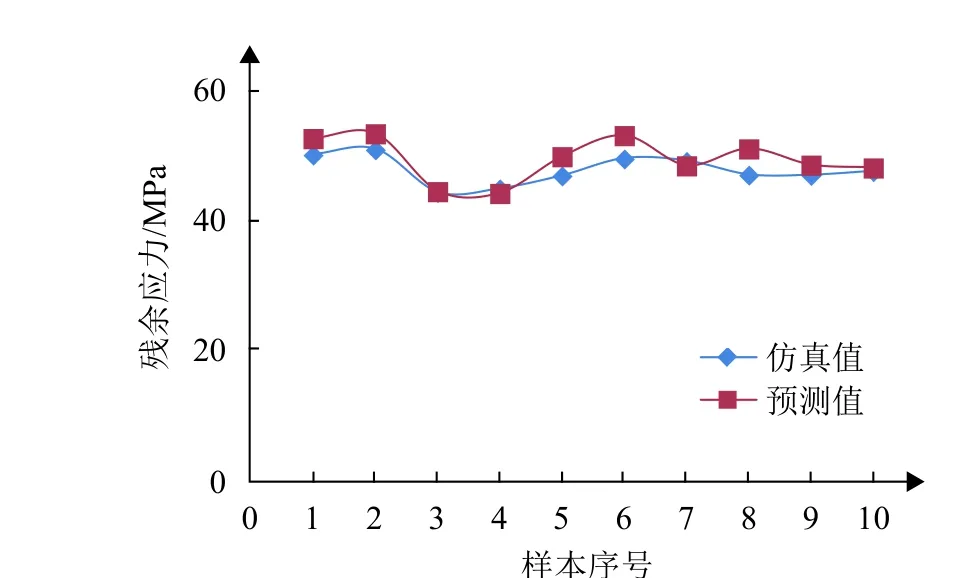
图10 带动量项BP 神经网络的预测值与仿真值对比
从表4 中数据可以看出,预测值和仿真值之间的相对误差均不超过10%,其中最大相对误差为7.93%,平均误差为3.19%。由图10 所示,可更直观的看出仿真值与预测值的误差大小。由此可见,本文所建立的带动量项BP 网络预测模型较好地实现了CSP 焊点焊后残余应力值的预测。
4 结 束 语
通过上述分析,可以得出以下结论:
1) CSP 焊点焊后残余应力随着焊点直径和焊点间距的增大呈上升趋势,而随着焊点高度和焊盘直径的增大呈下降趋势。在置信度为95%时,焊点直径、焊盘直径和焊点间距对CSP 焊点残余应力影响显著,灵敏度从大到小的排序为:焊点直径>焊盘直径>焊点间距。
2)带动量项BP 神经网络可以实现对CSP 焊点再流焊焊后残余应力的预测。预测值和仿真值之间的相对误差均不超过10%,其中最大相对误差为7.93%,平均误差为3.19%。
