基于模型补偿的逆变器交流电压自抗扰控制

2021-01-21霍思敏徐宇新黄勇李武龙聂静

电气传动 2021年2期

霍思敏，徐宇新，黄勇，李武龙，聂静

（1.国网湖南省电力有限公司，湖南长沙 410007；2.北京中恒博瑞数字电力科技有限公司，北京 100085；3.国网重庆市电力公司，重庆 400014）

逆变器作为系统的能量转换核心，一直以来都是电力电子领域的研究热点[1-2]。然而，由于开关器件的非线性特征、死区、非线性/突变负载等因素的存在，传统控制下逆变器输出波形质量难以保证。

韩京清［3］教授提出了自抗扰控制（active disturbance rejection control，ADRC）算法，ADRC 模型依赖度低，控制精度高、响应快并且抗扰能力强。最早提出的非线性ADRC，存在算法复杂、参数众多、参数调节困难等问题，限制了非线性ADRC的广泛应用[4]。高志强[5]教授为此对其进行了线性化（linear ADRC，LADRC）改造，LADRC保留了传统非线性自抗扰算法的特有优势，将众多参数归结为观测器带宽和控制器带宽的整定，调参过程大为简化，大大提高了工程实用性[6-8]。

自抗扰技术在换流器控制领域引起了研究人员的兴趣，文献[7]提出了基于非线性ADRC的并联型有源滤波器电流内环控制策略；文献[8]在文献[7]的基础上，利用Lyapunov稳定性理论证明了控制系统的渐进稳定性；文献[9]设计了VSC直流电压外环一阶自抗扰控制器，构造了基于反正切函数的光滑非线性状态反馈函数，有助于控制器收敛速度的提升，控制力抖振问题得到了较好的解决；文献[10-11]研究了自抗扰控制在级联型STATCOM静止无功补偿器电流解耦控制、直流电压控制中的应用。

上述研究内容着重将自抗扰控制技术应用于系统某一环节，替换原来的比例积分调节器，鲜有研究从被控对象具体特征出发、系统地设计ADRC控制器。本文以逆变器三相交流电压为被控对象，基于d-q同步旋转坐标系，进行控制系统数学建模，根据被控对象阶数，设计二阶LADRC，基于滤波电感电流可测的特点，引入相应的模型补偿项以降低线性扩张观测器（lineay extended state obseyvey，LESO）的观测压力。基于频域法，对双环PI控制和LADRC控制的动、稳态性能进行了对比分析。通过实验对传统LADRC、模型补偿LADRC和双环PI控制进行了进一步对比验证。

1 三相逆变器建模

三相三电平逆变器结构如图1所示，r，L和C分别为滤波电感内阻、滤波电感及滤波电容；iLa，iLb，iLc为逆变器三相电感电流；ioa，iob，ioc为三相负载电流；Ua，Ub，Uc为逆变桥侧三相电压；Uoa，Uob，Uoc为输出电压。

图1 三相逆变器拓扑结构Fig.1 Structure of three phase inverter

由图1可知，基于派克变换，可得到三相逆变器在d-q同步旋转坐标系下的模型：

式中：Uod，Uoq为输出电压再d，q轴分量；iLd，iLq为LC滤波电流d，q轴分量；iod，ioq为负载电流d，q轴分量；Ud，Uq为逆变器侧电压d，q轴分量；Uod，Uoq分别为输出电压d，q轴分量；ω为系统基频；∇为微分算子d/dt。

三相逆变器是一个多变量、负载扰动剧烈的系统，并且在派克变换后的d-q旋转坐标系下，变量间存在强耦合。采用传统PI双环控制难以取得满意的控制精度和抗扰性能。

2 三相逆变器传统LADRC设计

LADRC控制器的整体结构如图2所示。

图2 LADRC控制器的整体结构Fig.2 Overall architecture of LADRC controller

图2中，三相逆变器为以电压Uod，Uoq为状态量的二阶系统，为此针对d，q轴分别设计一个二阶LADRC。在自抗扰体系下，d，q轴间耦合归结为扰动，此时d，q轴的LADRC结构一致，为简化分析，下文以d轴为例展开。

将式（1）中的总和扰动扩张作为新的状态，可得如下的状态方程：

式中：b0为控制增益；KPWM为逆变桥增益；u为控制量；x1，x2为系统状态变量，对应输出电压及其导数；x3为扩充的状态变量；f˙(y,y˙,v,w)为系统总扰动，简记为f；h为f的微分。

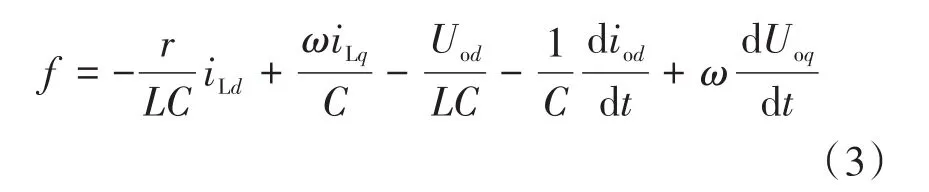
根据状态方程式（2），可建立如下三阶LESO：

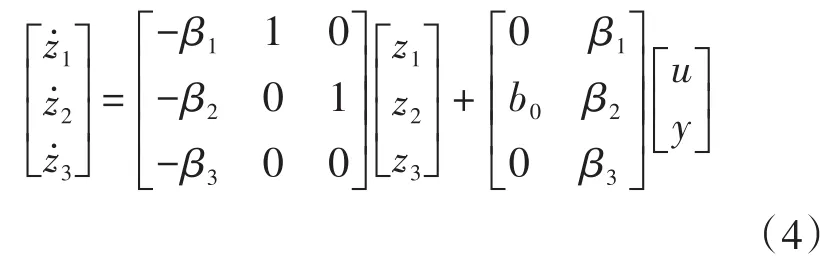
状态误差反馈律LSEF设计为

式中：kp，kd为反馈率比例和微分项增益；u0为原始控制量；v为参考量输入。

参考高志强教授[5]提出的带宽参数调节理论，LESO和线性状态误差反馈（lineay state error feedback，LSEF）的参数可简化为

式中：ωc为控制器带宽；ωo为LESO带宽。

如此一来，LADRC调参问题便可归结为LESO带宽ωo和控制器带宽ωc的设计，降低了调参难度。

3 引入模型补偿的LADRC

作为LADRC的核心，LESO的扰动观测水平直接影响系统的抗扰能力。针对阶跃扰动，LESO可对状态量快速收敛。然而，当扰动较大时，LESO存在幅值和相位的跟踪偏差。

针对传统LESO对扰动的观测问题，基于被控对象的实际情况，引入已知建模动态，以降低LESO的扰动观测压力，保证估计精度。

考虑总和扰动式（3），将其改写为

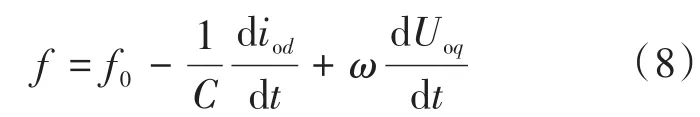
其中

式中：f0为系统已知扰动项。

扩张状态观测器重构为

状态误差反馈律LSEF重新设计为

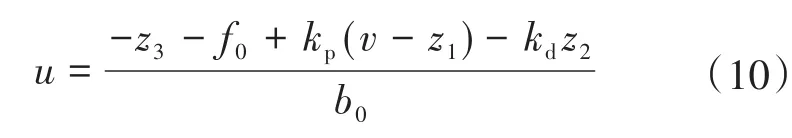
上述引入模型补偿的LADRC控制器能最大限度地利用已知建模动态，从而提高了系统的跟踪性能。

下面对LADRC控制下逆变器的跟踪性能进行分析。定义逆变器输出电压跟踪误差为：e=vy，结合式（2）和式（10），可得：

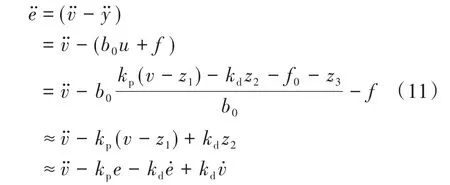
对式（11）进行拉氏变换，结合式（7），整理得：

由式（12）可见，所设计的LADRC控制器，对于给定参考信号为阶跃信号，系统的跟踪误差为零。考虑到论文是在d-q旋转坐标系下进行LADRC控制器设计的，参考信号为直流量，因此系统满足对参考信号的无差跟踪要求。

4 LADRC抗扰特性分析

4.1 模型补偿LADRC跟踪误差分析

抗扰能力是LADRC最为突出的特征，下面对其进行分析。

联立式（9）、式（10）可得：

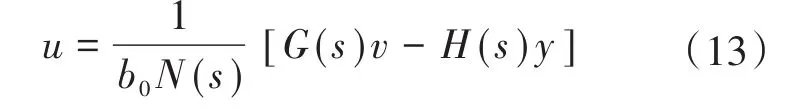
其中

被控对象记：

联立式（13）和式（14），可得模型补偿LADRC等效控制框图如图3所示。

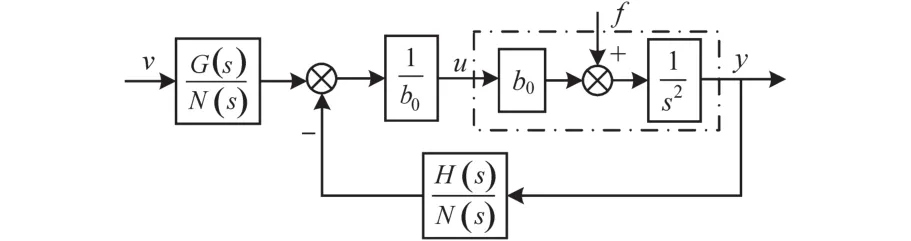
图3 模型补偿LADRC等效控制框图Fig.3 Equivalent control block diagram of model compensation based LADRC

根据图3可得模型补偿LADRC控制系统闭环传递函数为

可见，模型补偿LADRC系统输出y由参考信号跟踪项和扰动项构成，跟踪项主要由ωc决定，ωc越高，对参考信号的响应速度越快，但要考虑系统稳定性和噪声问题。扰动项取决于LESO的性能，模型补偿LADRC抗扰性能分析如图4所示，可见随着ωo增加，LESO扰动估计水平提高，相应的，系统抗扰能力也随之增强。

图4 模型补偿LADRC抗扰性能分析Fig.4 Analysis of disturbance rejection capability of LADRC with model compensation

4.2 LADRC与双环PI控制抗扰性能对比分析

三相逆变器的扰动主要来自于负载电流，如非线性负载、突变负载等，下面予以分析。

图5为三相逆变器模型补偿LADRC系统结构框图。由图5推导可得关于输出电压的传递函数为

式中：Uo为逆变器输出电压；Uref为电压参考值；io为负载电流；Gu（s）为Uref到Us传递函数；Zo（s）为io到Uo传递函数，具有阻抗性质。

图5 逆变器模型补偿LADRC系统结构框图Fig.5 System structure block diagram of model compensation based LADRC for inverter

根据文献[12]，传统LADRC控制系统闭环传递函数如图6所示。

图6 逆变器传统LADRC系统结构框图Fig.6 System structure block diagram of conventional LADRC for inverter

图6中，GN（s）和HN（s）分别为

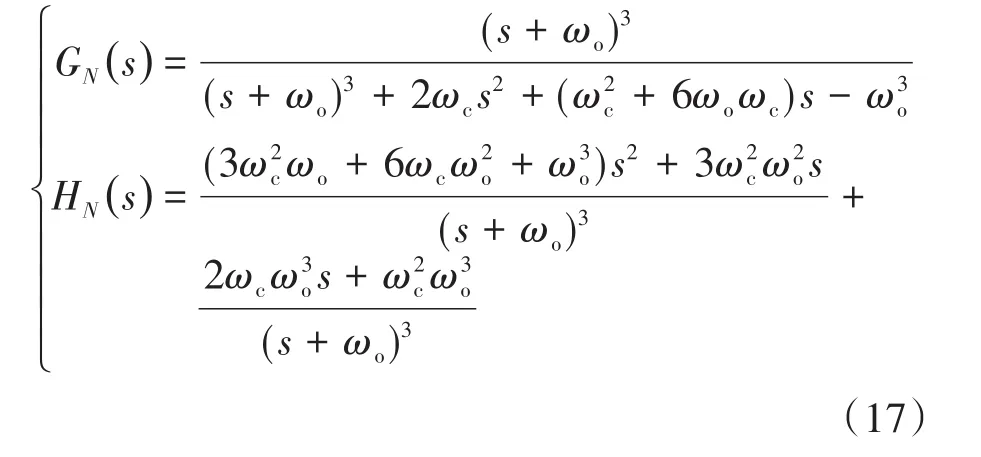
采用同样方法，可以得到三相逆变器传统LADRC系统关于输出电压传递函数：

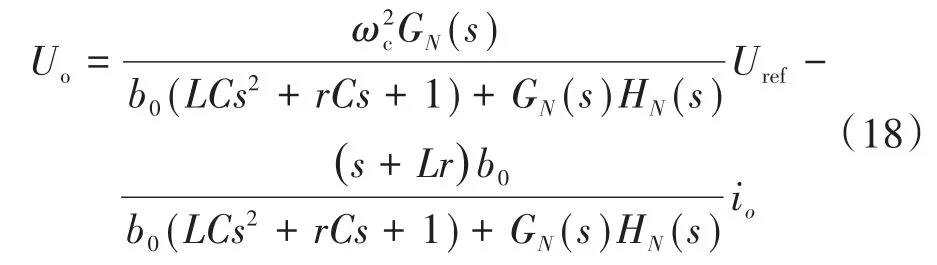
图7为双环PI、传统LADRC以及模型补偿LADRC控制系统等效阻抗Zo（s）的频率特性曲线。

图7 逆变器扰动项等效阻抗频率特性Fig.7 Frequency characteristic of equivalent impedance of disturbance for inverter

图7中，在低频段，三者的幅频特性基本相同，在中低频段，模型补偿LADRC对应的幅频特性曲线始终位于双环PI以及传统LADRC对应的幅频特性曲线下方，即模型补偿LADRC对应Zo（s）幅值较双环PI及传统LADRC的要小，能更好地抑制来自负载的扰动；在高频段，两者的频率特性曲线相近，LESO对高频扰动估计能力有限。

5 实验分析

为验证本文所提基于模型补偿的LADRC策略优势，设计了以德州仪器公司的DSP28335芯片为控制核心的三相三电平逆变装置，装置经隔离变压器后供负载接入。隔离变压器连接组别为Δ-Y，二次侧中性线引出以供单相负载接入。从LESO扰动估计能力、带不平衡负载、带非线性整流负载、突变负载等方面对双环PI控制、传统LADRC以及模型补偿LADRC控制3种策略进行了对比实验。

系统参数如下：电感L=0.74 mH，采样步长50µs，电容C=20µF，直流电压660 V，寄生电阻r=0.1 Ω，Kpwm=0.176。控制器参数如下：电压环比例系数0.21，观测器带宽ωo=9 800，电压环积分系数710，控制带宽ωc=5 500，电流环比例系数38，增益b0=Kpwn/(LC)。图8为整流负载试验波形。

图8中，在单相整流负载下，双环PI控制、传统LADRC、模型补偿LADRC输出A相电压波形畸变率分别为4.12%，3.52%和2.15%。三相整流负载下，三种控制策略对应电压波形畸变率分别为4.53%，3.85%和2.34%。

图9为逆变器在负载突变时输出电流和电压波形。

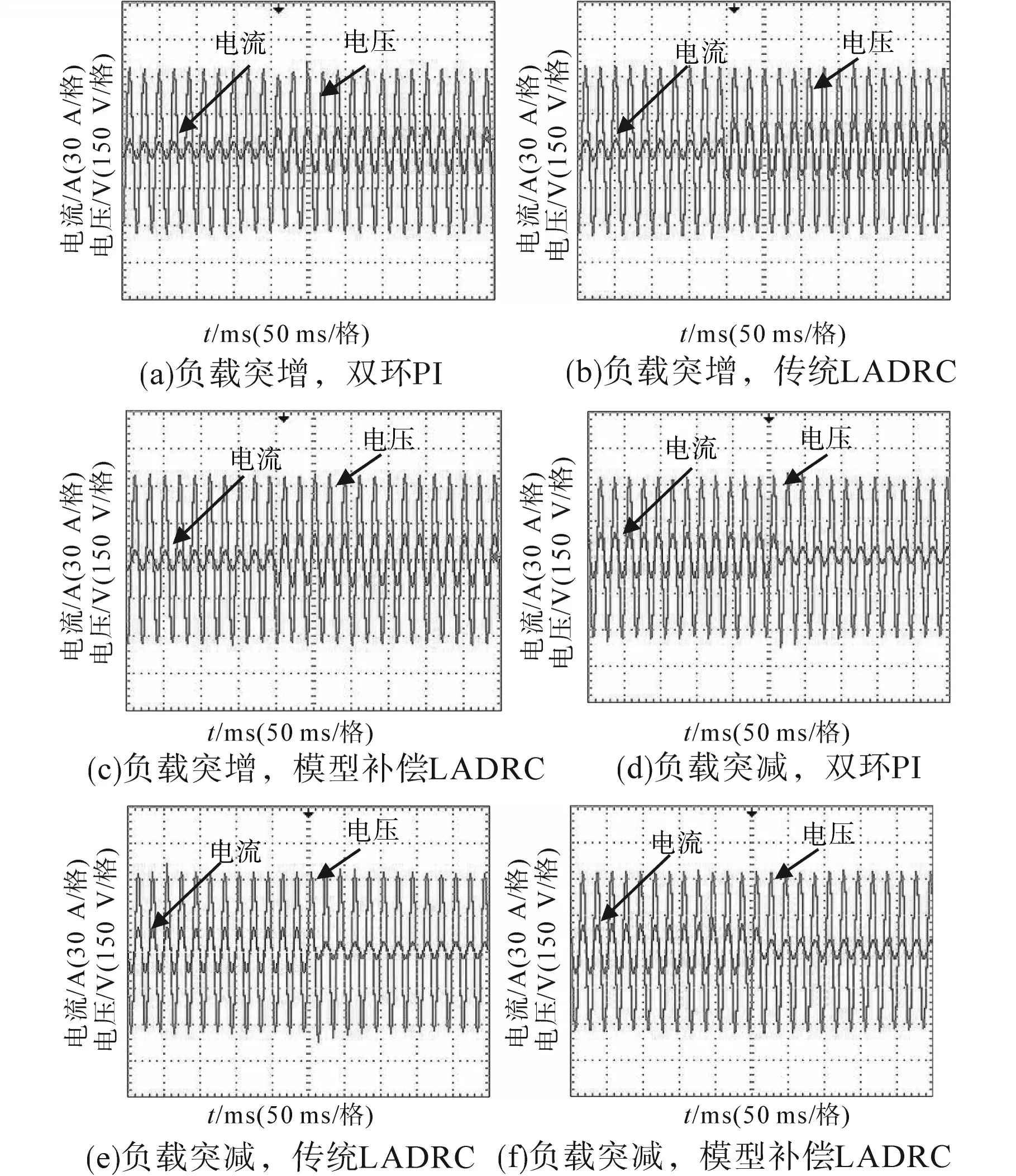
图9 逆变器在负载突变情况下输出电压、电流实验波形Fig.9 Voltage and current output experimental waveforms of inverter under condition of load mutation

图10为逆变器在负载突变情况下多种控制方式下电压有效值曲线。

图10 负载突变工况下逆变器电压有效值Fig.10 Voltages RMS of inverter under condition of load mutation

由图10可知，突增负载情况下，由20%增加到80%，此时三种策略对应的逆变器电压凹陷幅度分别为6.9 V，4.5 V及3.8 V，电压恢复时间分别为47 ms，35 ms及29 ms。突减负载情况下，由80%减到20%，此时三种策略电压超调分别为6.3 V，3.4V及2.7V，恢复时间分别为45ms，33ms及26ms。由上述的非线性负载和突变负载实验可见，LADRC的负载扰动抑制能力要强于双环PI控制。