基于改进滑模频移法的孤岛检测算法研究

胡丹丹，赵倩，许昊，朱哲然，龙洁，朱立尧

（1.国网河南省电力公司焦作供电公司，河南 焦作 454150；2.重庆大学电气工程学院，重庆 400044）

随着分布式并网光伏发电系统技术的快速发展，越来越多的分布式系统并入电网中，对其供电的可靠性和安全性要求也日益提高，同时一些问题也凸显而出，其中比较典型的便是“孤岛效应”。孤岛效应可能会造成电能质量降低、本地负载损坏、工作人员触电等危害[1]，因此及时有效地检测出孤岛效应便显得尤为重要，我国于2005年发布了孤岛检测的相关标准，要求光伏逆变器设备至少具备一种孤岛检测方法且必须保证孤岛发生时设备在2 s内切除电网。目前常见的孤岛检测法可分为三类：远程通信法、被动检测法及主动检测法。文献[2-6]介绍了各类检测方法的优缺点。

滑模频移法（slip-mode frequency shift，SMS）是主动检测法的一种，其通过扰动电流相位的方式使得频率越限，从而实现孤岛检测。文献[7]提出一种基于模糊控制的改进SMS法，优化了扰动系数的选取。文献[8]提出在检测算法中加入额外的相角偏移量，以此提高检测可靠性，但也加大了扰动对电能质量的影响。文献[9]提出了一种将滑模频移法和相位突变法结合的混合检测法，但实际情况中，由较小扰动引起的相位突变阈值难以整定。

SMS法具备对电能质量影响小、能消除特定负载品质因数（通常为2.5）以下的检测盲区等优点，但存在检测初始时刻负载曲线和扰动曲线提前重合，进而导致检测速度大幅降低甚至检测失败的问题，为改善这一问题，并提高检测速度、进一步降低对电能质量的影响，提出了一种改进SMS检测算法，文中对其可行性和有效性进行了分析，并通过PSIM仿真软件和实验平台进行验证。

1 传统SMS法分析

传统的滑模频移法通过改变公共耦合点（point of common coupling，PCC）处电流相位的方式扰动PCC处的电压频率，孤岛情况下，电压频率失去主电网的钳制，会产生一定程度的变化，而频率的变化会进一步加大相位变化量，直至频率到达稳定点，即通过正反馈的作用使逆变器输出电压的频率迅速脱离正常的频率波动范围，进而检测出孤岛。

传统滑模频移法的扰动函数可表示为

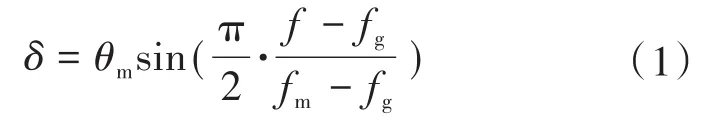
式中：θm为最大移相角（可视为扰动系数）；fm为最大移相角对应的频率；f为公共耦合点处电压频率；fg为电网频率，一般为50 Hz。

图1为PCC处电压相位与频率之间的关系，其中直线为本地负载的相位响应，曲线为滑模频移法扰动函数的相位响应。B点为系统正常运行时的额定频率点，孤岛状态下，频率会受到扰动和本地负载的影响发生偏离，最终稳定在A点或C点。

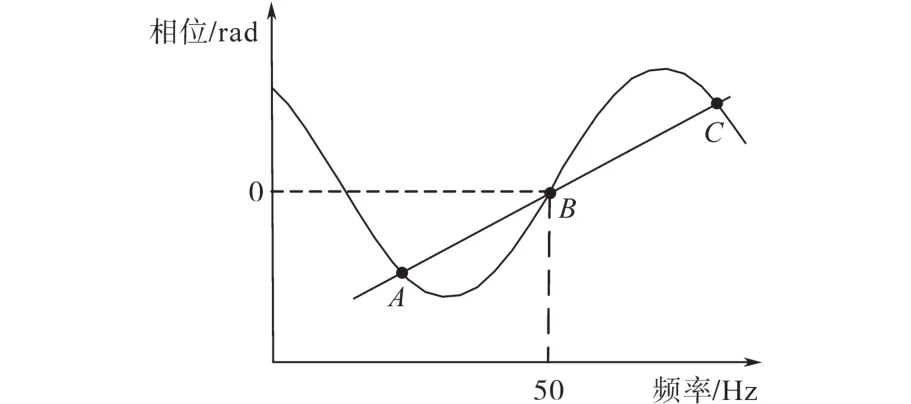
图1 滑模频率偏移法的相位与频率的关系Fig.1 The relation between phase and frequency of SMF migration method

将图1相位响应局部放大，如图2所示。

图2 滑模频率偏移法的相位与频率的关系局部放大Fig.2 Relation between phase and frequency of SMF migration method with local amplification

图2中，初始状态下，频率f位于B点，受到本地负载的影响，PCC处电压频率f会发生微小的偏移，至B′点，该频率在扰动曲线所对应的干扰点为C′点，f受其影响朝着C′点的方向继续发生偏移至B"（B"对应的相位响应与C′点一致）点，此时干扰点为C"点，不断重复这一过程形成反馈，f会不断发生偏移，直至负载曲线和扰动曲线相交，f最终达到稳定。

图3为不同扰动系数下滑模频移法相位与频率关系图，其中，直线为品质因数为2.5的本地负载的相位响应，当扰动函数响应曲线的初始斜率小于负载响应曲线（对应扰动系数θm=1°），扰动无法产生有效作用，反馈无法形成，如果扰动系数不够大（θm=3°），会在频率越限之前提前达到稳定点，因此需要合理选择扰动系数的值。随着扰动系数的增加，扰动函数的初始斜率会不断增加，越容易形成反馈，但在系统正常运行情况下的干扰量也随之增大，即对电能质量的不利影响愈加严重。

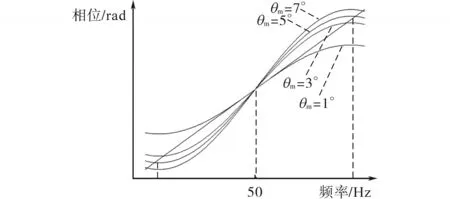
图3 不同扰动系数下滑模频移法相位与频率关系Fig.3 The relation between phase and frequency of SMS with different perturbation coefficients

综上可知，滑模频移法的实现需满足如下两点：1）B点处扰动函数的初始斜率应大于负载曲线的斜率；2）A点或C点处的频率不在系统正常频率波动范围内。

为适应我国光伏逆变器的实际情况以及对于孤岛检测的要求，通常令θm=5°，fm-fg=1 Hz，在该参数下相位扰动可使频率迅速脱离出49.5～50.5 Hz的频率范围，且对于品质因数Qf≤2.5的负载无检测盲区，因此可以较好的检测出Qf≤2.5时的孤岛情况[10]。

由于系统正常运行时，频率波动范围为49.8～50.2 Hz，因此在 Δf=±0.2 Hz时，将f-fg=0.2 Hz，θm=5°，fm-fg=1 Hz代入式（1），求解得到δ扰动=1.54°，此角度即为滑模频移法在系统正常运行时的扰动角，其可以反映所施加的扰动对电能质量的影响。

由以上分析可知，滑模频移法是通过反馈的方式不断增加扰动量，直至频率越限。由图2可见，当扰动系数较低时，在初始时刻附近，负载曲线与扰动曲线接近重合，一些微小的扰动都可能导致B′点和C′点提前重合，使得反馈作用无法可靠形成，进而导致检测速度大幅降低，甚至检测失败，因此扰动函数的初始斜率大小尤为重要。

2 改进SMS算法原理分析

2.1 改进滑模频移法提出

为减小SMS算法对电能质量的影响，并提高孤岛检测速度，避免孤岛发生初始时刻扰动曲线与负载曲线提前重合进而导致检测速度降低甚至检测失败的问题，文章提出一种改进型滑模频移孤岛检测方法，对传统SMS算法的扰动函数进行改进优化，改进算法的扰动函数表达式为

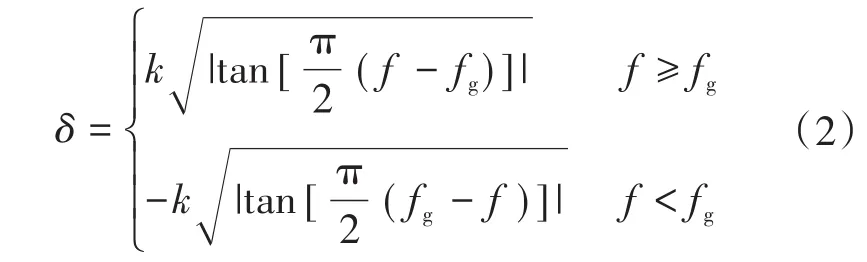
式中：k为扰动系数。

该函数的曲线如图4所示，可见扰动函数的初始斜率为无穷大，可以满足在较高品质因数条件下，负载曲线初始斜率始终小于扰动曲线的初始斜率，因此即使系数k设定值很小，初始时刻扰动曲线也会迅速脱离负载曲线附近，不会与负载曲线提前重合，使得反馈作用可以更加快速、可靠地形成，进而保证检测可靠性并提高了检测速度。

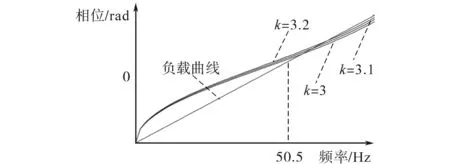
图4 改进滑模频移法的相位与频率的关系Fig.4 The relationship between phase and frequency of improved SMS method

为有效地实现孤岛检测，需要对扰动函数中的扰动系数k值进行整定，与传统SMS算法类似，扰动系数过小，可能导致检测速度降低甚至检测失败；扰动系数过高，虽然可以消除特定品质因数下的检测盲区，但也加大了扰动对电能质量的影响。因此需要设定合理的扰动系数，扰动系数k的整定过程如第2.2节所述。

2.2 改进算法盲区分析及扰动系数整定

由于扰动函数具备初始斜率无穷大的特点，因此仅需考虑第1节条件2），即稳定点的频率越限（49.5～50.5 Hz），采用Qf0×Cnorm空间描述法对扰动系数k进行整定，其中横坐标采用类负载品质因数的参数Qf0，纵坐标采用的“标准化电容”Cnorm，可表示为

其中

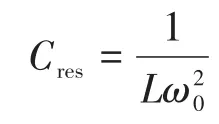
式中：R，L，C分别为本地负载的电阻、电感、电容值；ω0为电网角频率。

Qf0×Cnorm空间描述法的相位判据为下式：

式中：φinv为特定反孤岛策略下逆变器输出电流超前于公共耦合点电压的相位角。

对于文章提出的改进滑模频移法，φinv可表示为

公共耦合点PCC处的角频率ω可表示为

式中：Δω为公共电网角频率的微偏量。

由式（4）“标准化电容”的定义可知：

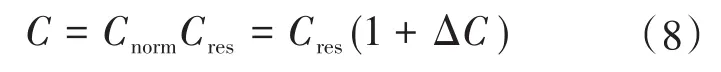
式中：ΔC为负载电容的微偏量。

联立式（3）～式（8），化简整理得到：

根据我国相关负载品质因数要求以及IEEE Std.929ㅡ2000的相关规定，取Qf0=2.5，Cnorm=1，ω0=2π×50 Hz，Δω=±2π×0.5 Hz，f-fg=0.5 Hz根据孤岛检测理论无盲区条件，令ΔC=0，将以上各参数代入式（9），化简得到：

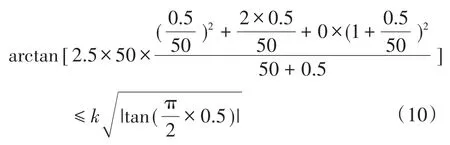
求解式（10），可得到k≥2.86，即k取2.86时，理论上改进滑模频移法不存在检测盲区，由于电网正常频率波动范围为Δf=±0.2 Hz，将f–fg=0.2 Hz，k=2.86代入式（2），求解得此时改进滑模频移法带来的扰动角δ扰动（k=2.86）=1.68°，可见此时扰动角较大，为降低初始扰动角，并进一步提高检测效率，选择设定可变的系数k，其参数整定过程如下：系统正常运行时，频率在49.8～50.2 Hz，可使扰动系数k在这一频率范围内较低，当频率脱离这一范围时，增大k值，以此加大扰动，加快频率越限速度。由于改进滑模频移法具备初始斜率为无穷大（远大于负载线斜率）的特点，因此初始较低的k值不会降低检测成功率。

为得到可变系数k的初始值，将Δf=±0.2 Hz代入式（9），得到下式：

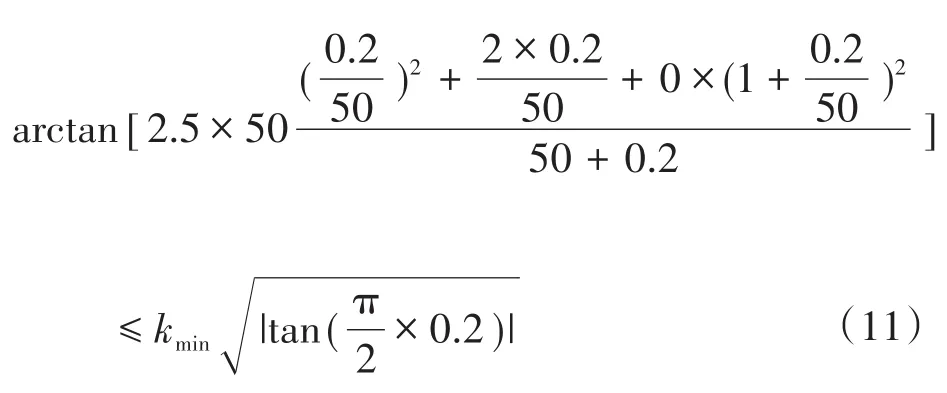
求解式（11）可得kmin=1.94，取kmin=2，此时可保证扰动使得频率变化量足以达到0.2 Hz，之后提高k值，取kmax=5，以此加快扰动速度。

在此扰动系数下，设置f–fg=0.2 Hz，kmin=2代入式（2），求解得此时扰动角δ扰动（k=2）=1.13°，而SMS法的扰动角δ扰动=1.54°，可见此时扰动带来的相位偏差有了较大程度的降低。

2.3 改进算法工作流程

我国相关标准对孤岛检测的规定是从检测出孤岛至逆变器断开的时间不能超过2 s，同时如前文所述，为减小算法在正常运行状态下对电能质量的影响，在正常情况下加入较小的扰动，一旦频率超过一定的范围，认为系统可能处于孤岛状态下，此时增大扰动，加速频率的越限速度。具体流程如下：

如果孤岛发生后，电压和频率的变化程度满足以下4个条件之一：1）f＞50.5 Hz；2）f＜49.5 Hz；3）UPCC＞1.10UN；4）UPCC＜0.88UN，即可直接通过PCC处的电压幅值或频率检测出孤岛，其中，UPCC为公共耦合点处的电压；UN为系统额定电压。

如果孤岛发生后，电压和频率的变化程度不满足以上4个条件，即需要额外加入扰动使频率越限才可以有效地检测出孤岛。文中所加入的扰动如下：

当公共耦合点处电压频率f满足49.8 Hz≤f≤50.2 Hz时，扰动函数如下式所示：

扰动函数的方向应与PCC处电压频率方向保持一致，即50.2 Hz＞f＞50 Hz时，施加k=2的正向扰动；49.8 Hz＜f＜50 Hz时，施加k=-2的负向扰动；当f位于f＜49.8 Hz或f＞50.2 Hz时，扰动函数如下式所示：

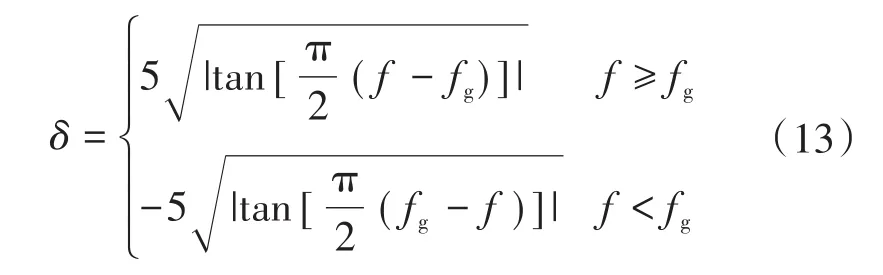
当f＜49.8 Hz，施加恒定的负向扰动1 s；反之，若f＞50.2 Hz，施加恒定的正向扰动1 s。如果在1 s内频率越限（f＜49.5 Hz或f＞50.5 Hz），则认为孤岛发生，立即断开逆变器；反之，认为是由其他问题引起的频率短暂超出正常波动范围（49.5 Hz＜f＜49.8 Hz或 50.5 Hz＞f＞50.2 Hz），重新进行检测流程。

图5为改进SMS算法整体流程图。

3 仿真及实验验证

3.1 仿真验证

图6、图7分别为SMS法和改进法在谐振频率50 Hz时的孤岛检测情况，三相电网在1.2 s时断电。本地负载为三相对称的RLC并联负载，其中电阻为20.88 Ω，电容为365.5µF，电感为24.58 mH，此负载所消耗的有功功率与逆变器提供的有功功率相等，因此在断网前后电压幅值不会产生变化，仿真测得此时负载谐振频率对应为50 Hz，该仿真环境为孤岛检测最不利情况。

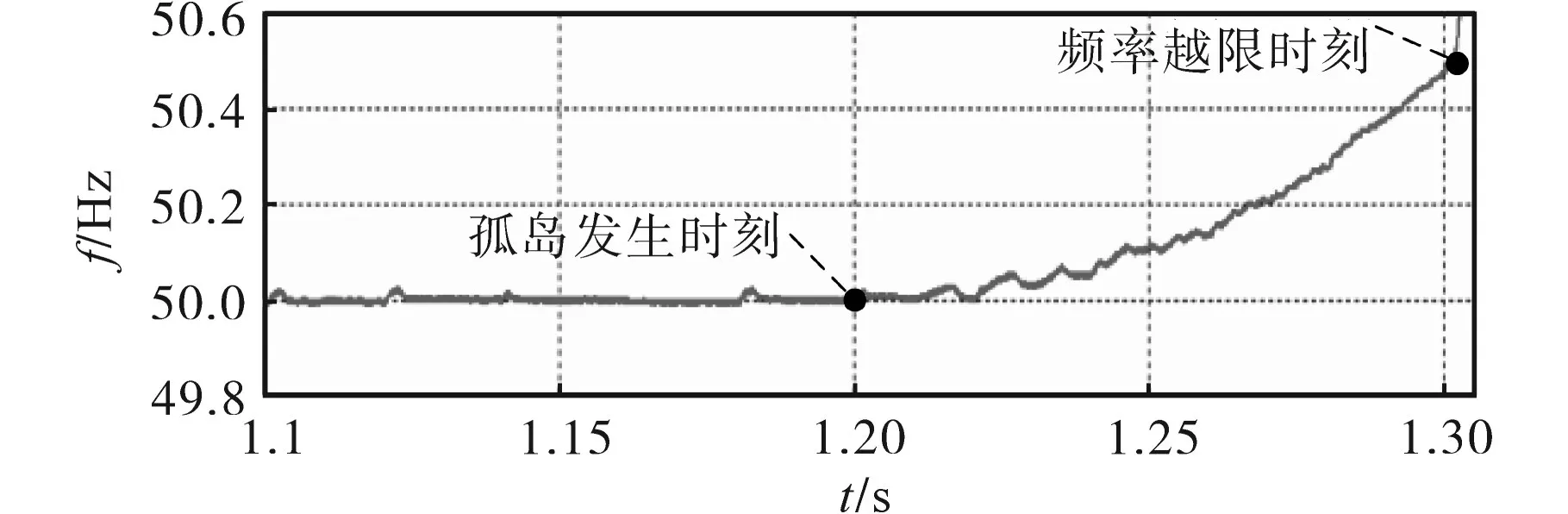
图6 SMS法在谐振频率50 Hz时的孤岛检测情况Fig.6 The islanding detection of SMS method at 50 Hz resonance frequency

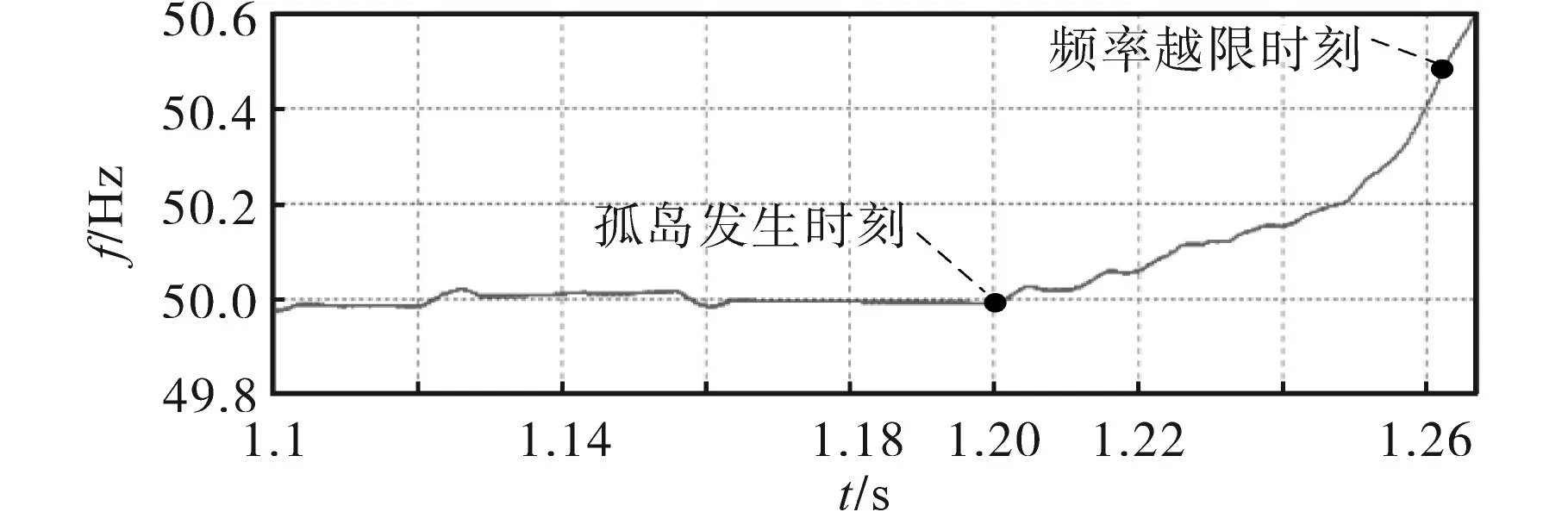
图7 改进法在谐振频率50 Hz时的孤岛检测情况Fig.7 The islanding detection of the improved method at 50 Hz resonance frequency

由图6、图7可以看出：两种检测法在谐振频率为50 Hz时所对应的孤岛检测速度，SMS法在孤岛发生后0.103 s会检测到频率越限，而改进法在孤岛发生后0.064 s即可检测到频率越限，检测速度有了较大的提升。

为测试两种方法在不同谐振频率时所对应的检测效果，改变三相负载为R=20.88 Ω，L=24.58 mH，C=358.5µF。此时所对应的谐振频率为50.1 Hz。SMS法和改进法的仿真结果如图8、图9所示。

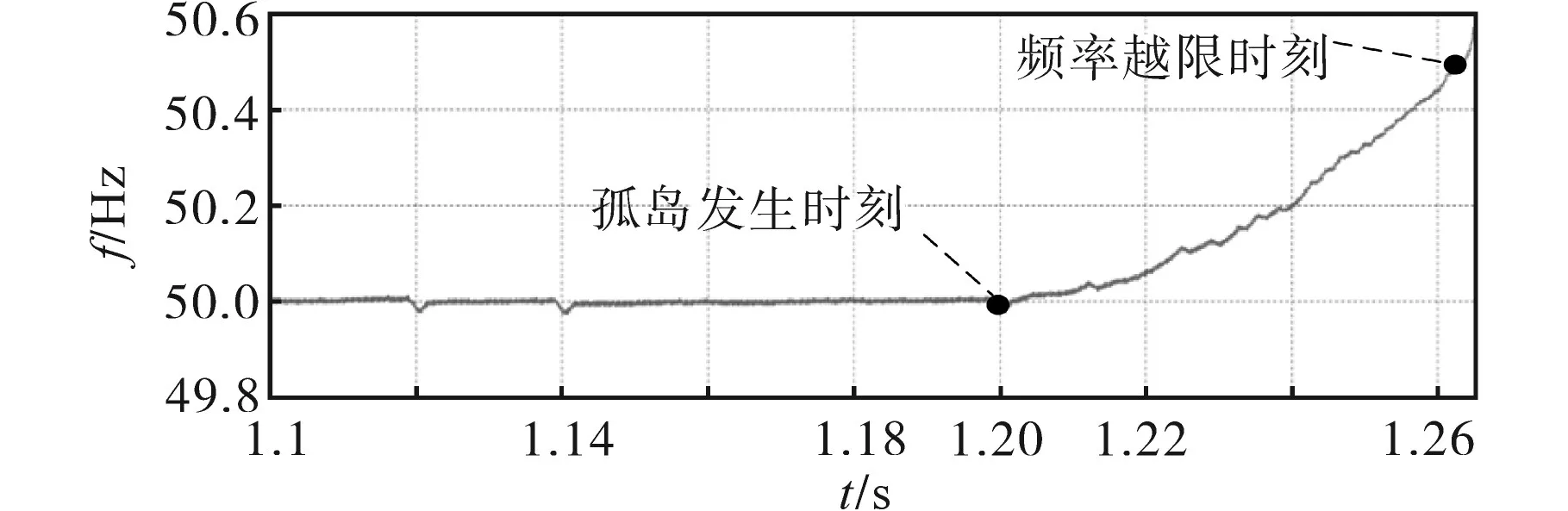
图8 SMS法在谐振频率50.1 Hz时的孤岛检测情况Fig.8 The islanding detection of SMS method at 50.1 Hz resonance frequency

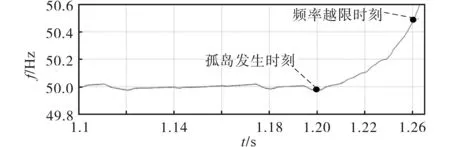
图9 改进法在谐振频率50.1 Hz时的孤岛检测情况Fig.9 The islanding detection of the improved method at 50.1 Hz resonance frequency

由图8、图9可以看出：两种检测法在谐振频率为50.1 Hz时所对应的孤岛检测速度，SMS法在孤岛发生后0.062 s会检测到频率越限，而改进法在孤岛发生后0.04 s即可检测到频率越限。

3.2 实验验证

为验证算法的有效性，搭建相应的孤岛检测实验平台，其中控制芯片选用DSP28335，功率器件选用IPM模块，三相电网电压有效值为79.5 V，频率50 Hz，直流母线电压260 V，采用LC滤波方式，L滤波=5 mH，C滤波=10µF，负载电感L=20.5 mH，电容C=590µF，实际测试得到此时对应的负载谐振频率为50.05 Hz，负载电阻为可变电阻，通过调整可变电阻来改变负载品质因数Qf，测得Qf分别为2.54和3.16，将SMS算法和改进算法的扰动函数加入并网控制算法，利用PSIM生成相应DSP代码，实验得到波形如图10、图11所示。

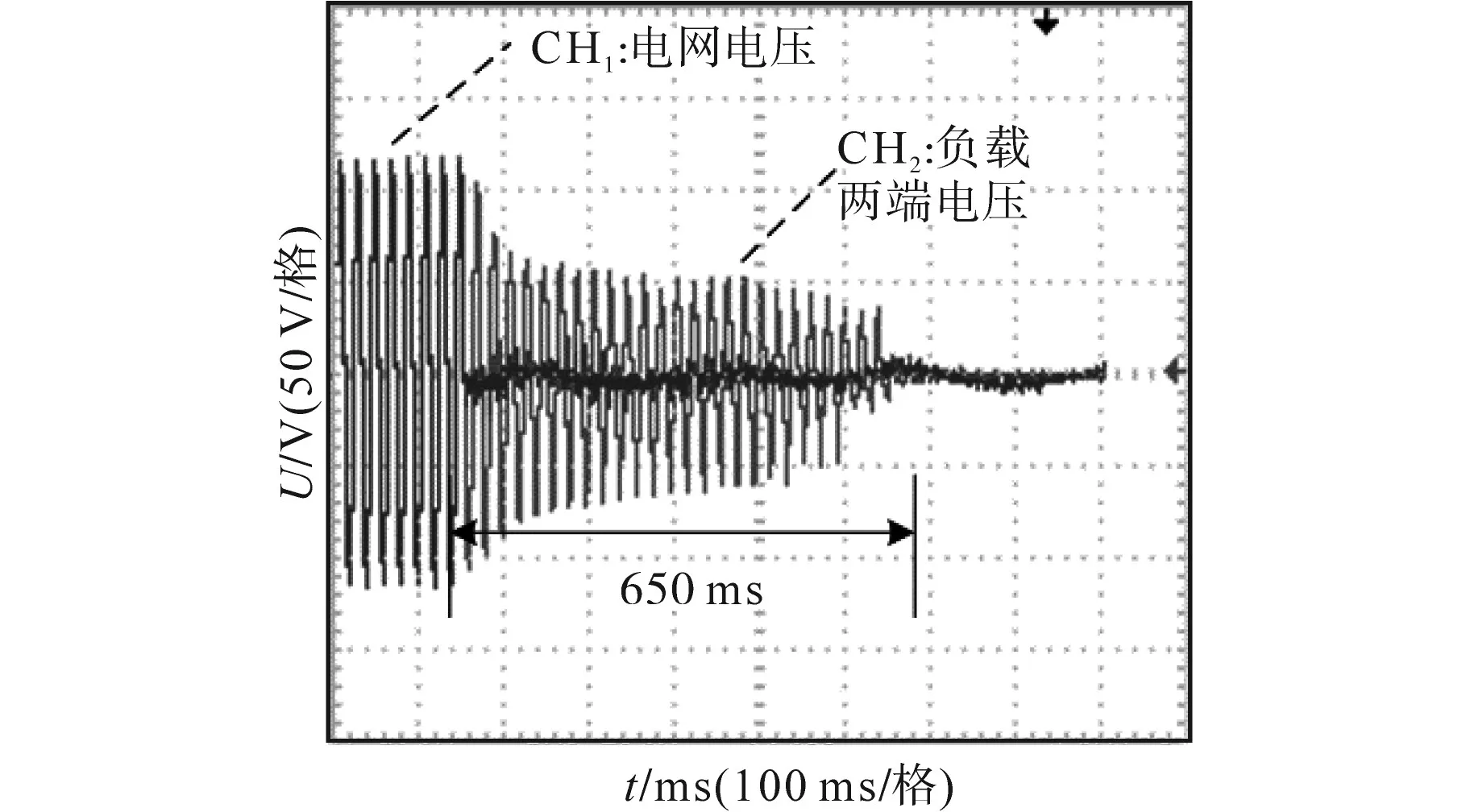
图10 SMS法，Qf=2.54断电时孤岛检测波形Fig.10 SMS method，Qf=2.54 isolated island detection waveforms

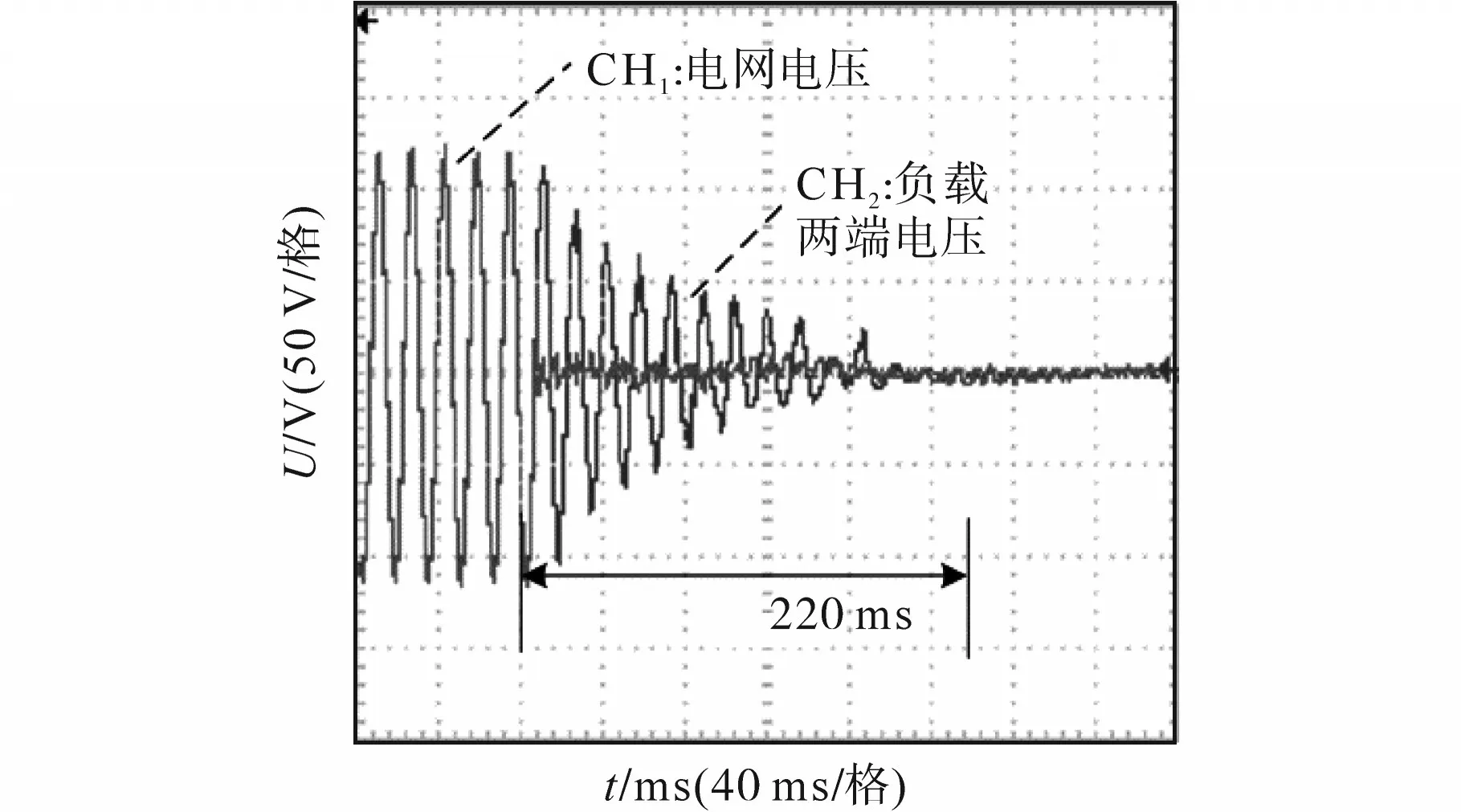
图11 改进法，Qf=2.54断电时孤岛检测波形Fig.11 Improved method，Qf=2.54，isolated island detection waveforms

图10、图11分别为SMS法和改进法在Qf=2.54，断电时的孤岛检测情况，CH1为电网u相电压波形，CH2为u相负载两端电压波形，可见CH1突变为0时即为电网断电时刻，由于频率还未越限，逆变器仍然在工作，因此负载两端仍有电压，当频率越限时，使逆变器输出断开，负载电压降为0。由图10和图11对比可以看出，SMS法从孤岛发生至逆变器输出电压降为0需要约650 ms，而改进法仅需约220 ms，可见检测速度有了较大的提升。

图12、图13分别为SMS法和改进法在Qf=3.16，断电时孤岛检测波形。

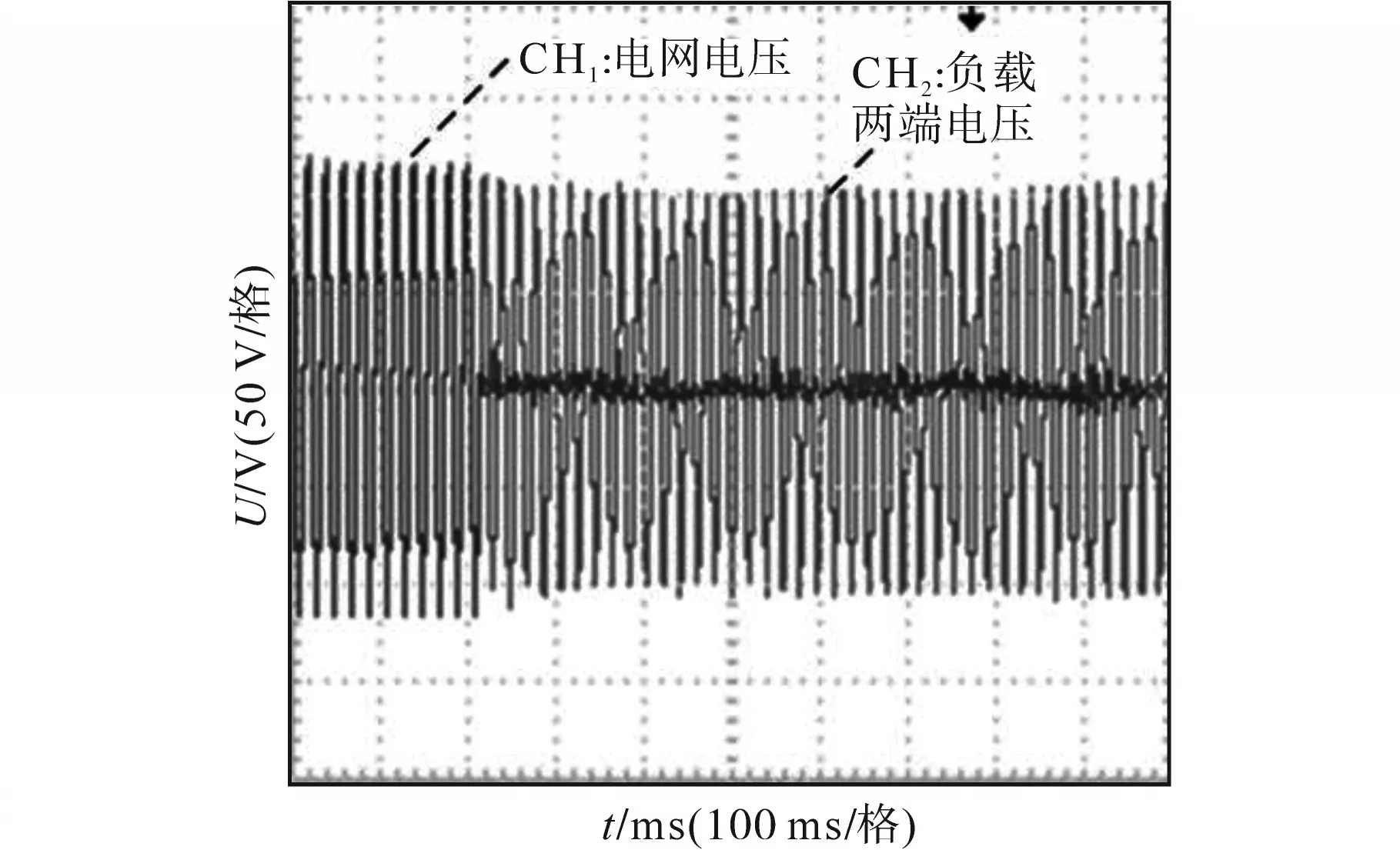
图12 SMS法，Qf=3.16断电时孤岛检测波形Fig.12 SMS method，Qf=3.16，isolated island detection waveform

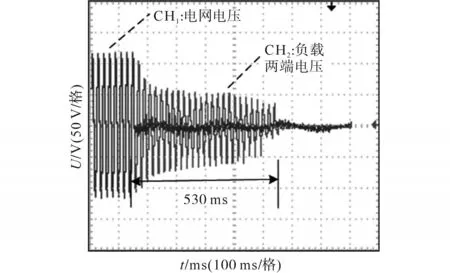
图13 改进法，Qf=3.16断电时孤岛检测波形Fig.13 Improved method，Qf=3.16，isolatedisland detection waveforms

由图12和图13对比可以看出，SMS法在扰动系数为5°时，无法有效检测出孤岛状态，而同情况下采用改进方法则可以有效检测出孤岛的发生，从孤岛发生至逆变器输出电压降为0需要约530 ms。通过实验结果看出，改进法较传统SMS法而言，在实物平台上能够适应更加恶劣的检测情况，同时也能保证检测速度。

4 结论

文章针对传统滑模频移法所存在的问题，提出了一种新的改进算法，利用改进函数的特点，使得负载曲线与扰动曲线不会提前重合，进而使得反馈作用可以有效产生，提高检测速度，同时使系统正常运行时检测算法所产生的扰动角（δ扰动）明显减小，从而降低了扰动对电能质量的影响。通过仿真和实验结果表明，所提出的检测方法，可以有效地提高检测速度和准确性。