虚拟同步发电机稳定性分析与参数设计

2021-01-21

电气传动 2021年2期

（国网北京市电力公司电力科学研究院，北京 100075）

虚拟同步发电机（virtual synchronous generator，VSG）是一种模拟同步发电机特性的控制策略[1]。VSG可工作在并网或孤岛模式，并且能够像不间断电源一样利用下垂特性均分负载[2]。VSG的惯性对电力系统稳定性尤为重要[3]。

VSG控制器的实现目前已有几种方案，VSG首次由Beck和Hesse在文献[4]中提出，其实现方案中将传统发电机的全阶模型作为控制系统的一部分。控制中电机模型输入为所测量的并网点电压，从而计算出电机电流，然后将这些电流作为电流滞环控制器的参考值来实现发电机特性模拟。文献[5]和文献[6]中设计了全阶模型的VSG方案，且改为电压源型设计，更准确地模拟了发电机特性。后续为了降低系统复杂度，将降阶模型代替全阶模型，不再考虑对同步发电机的电磁暂态模拟，而只是引入了惯性和阻尼[7]。文献[8]和文献[9]中的VSG最为简单，直接采用转子方程来实现惯性，即由转子方程和无功功率控制器结合一起为PWM生成模块提供电压参考。该设计确保了控制器结构简单，惯性模拟和无功功率控制确定的电压参考值可以输入到电压电流双闭环级联控制器的内部。该控制方案可方便地实现电流和电压限制，以保护逆变器免受过流影响并避免意外的过调制。尽管使用电压电流双闭环级联控制器可方便地实现逆变器控制，但相对较多的控制器参数和各个环路之间的相互作用使参数整定变难，同时还需详细分析系统稳定性[10-11]。

对此，先介绍传统的控制器参数整定。然后，导出VSG线性化状态空间模型，利用特征值评估小信号稳定性。分析结果表明，如果逆变器以低开关频率（如2～3 kHz）运行，则内环电流控制器的带宽受到限制，从而导致系统失稳。因此，提出了一种由线性化模型的特征值的灵敏度矩阵引导的VSG参数调整方法。利用特征值的灵敏度可识别对临界模态影响最大的参数，同时利用迭代算法将系统特征值从临界位置移开，从而增强系统稳定性。最后，通过对比仿真验证了所提出参数整定方法的有效性。

1 VSG控制策略概览

本文的研究对象为并入电网或者带负载的三相逆变器，逆变器输出端包含有LC滤波器。图1为所分析的逆变器配置示意图。

图1 所分析的逆变器配置示意图Fig.1 Schematic of the analyzed inverter configuration

本文设计的系统主要参数如下：额定容量Sb=1 MV·A，额定输出线电压有效值US_LL_RMS=690 V，LC滤波器电阻R1=0.003（标幺值），LC滤波器电容C1=0.074（标幺值），LC滤波器电感L1=0.08（标幺值），VSG虚拟惯性时间常数Ta=2 s，VSG阻尼系数kd=10 000，额定电网频率fn=50 Hz，电源电阻Rs=0.003（标幺值），电源电感Ls=0.1（标幺值）。以下分析将以这些参数为基础。为了简化分析，假设直流链路上的储能单元所蕴含的能量等效于VSG模拟的电机旋转惯性。

1.1 同步参考坐标系中的电气模型

逆变器在忽略开关暂态后可由连续时间平均模型描述：

式中：L1，C1，R1分别为滤波电感、滤波电容和寄生电阻；iLd，iLq分别为电感电流d，q轴分量；uLd，uLq分别为电感前端电压d，q轴分量；iOd，iOq分别为逆变器输出电流的d，q轴分量；uOd，uOq分别为逆变器输出电压的d，q轴分量；ωb，ωpu分别为频率基值、标幺值。

逆变器侧滤波电感方程如式（1）所示，滤波电容方程由式（2）给出。网侧或负载侧可由RL电路描述，相应模型形式和式（1）一样。

1.2 基于VSG的控制系统

图2为基于VSG的逆变器控制器结构。

图2 基于VSG的逆变器控制器结构Fig.2 Controller structure of the VSG-based inverter

从图2中可看出，控制系统含有五部分，其中控制器末端为PWM调制模块，然后依次是基于同步参考坐标系的电流、电压控制环，无功功率下垂控制模块和VSG惯性和阻尼模块。q轴电压参考值等于0，同步参考坐标系定向到滤波电感电压矢量上，d轴电压参考则是由传统的无功功率下垂控制器提供的。同步参考坐标系的相位角是根据下式给出的转子方程对惯性和阻尼模拟后输出的频率进行积分得到的。

式中：Tv为虚拟转矩；ωpu，ωgpu分别为角频率标幺值、电网角频率标幺值；P*，P分别为有功功率设定值和实际测量值；kd为下垂系数；s为算子。

如果逆变器在并网模式下运行，则VSG通过转子方程的功率平衡与电网电压相角同步。因此，VSG的正常运行时不依赖于任何电网同步算法，如锁相环等。与传统的发电机一样，VSG本身也具有孤岛运行的能力。

2 传统的VSG控制器参数整定

2.1 电流闭环参数设计

为了对图2中所示电流闭环参数进行设计，需考虑逆变器PWM工作模式的延迟效应。采用一阶传递函数近似PWM的影响，并假设测量电压的前馈和d，q轴电压理想解耦，则电流控制器的开环传递函数hcc，dq可定义如下：

其中

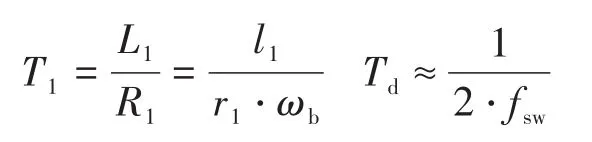
式中：kpc，kic分别为电流闭环PI调节器的比例、积分系数；L1，R1分别为滤波电感、滤波电阻标幺值；l1，r1分别为滤波电感、滤波电阻实际值；T1为滤波电感时间常数；Td为延迟效应近似时间常数；fsw为开关频率。

基于式（4），按照极点抵消原则来选择增益，从而产生临界阻尼闭环传递函数，对应kpc和kic的计算式如下：

由式（5）可知，PI参数和带宽直接受逆变器开关频率限制。以开环传递函数极点抵消原则设置参数得到的系统相角裕度约为65°，可进一步降低相角裕度以获取更多的控制器增益和带宽。

2.2 电压闭环参数设计

从图2中的级联控制器结构可看出，电压闭环参数受到电流控制带宽的限制。为了简化，将电流控制器用一阶传递函数近似。假设d，q轴理想化去耦，则电压开环传递函数为下式：

式中：kpu，kiu分别为电压闭环PI调节器的比例、积分系数；C1，c1分别为滤波电容标幺值、实际值；Teqcc为电流闭环时间常数；TC为滤波电容积分时间常数。

电压闭环参数是根据确保电压开环传递函数的穿越频率处最大相角裕度的原则设计的。增加设计参数a将电压闭环PI调节器的参数整定和闭环传递函数阻尼因子ζ关联，如下所示：

其中

传统参数整定要求电压环和电流环间带宽保持较大差异。这是通过增大a的值来保证的，直到电压闭环带宽比电流控制带宽低至少十倍。

3 稳定性和参数敏感度分析

对于图2中所示的VSG控制方案，必须显著降低电压控制闭环的带宽，否则无法确保无功功率控制和虚拟惯性控制的预期性能以及整个控制系统的稳定性。而如果电流控制闭环带宽较低，则可能发生不同控制回路之间的相互作用。故下面对控制系统稳定性和动态性能开展分析。

3.1 状态空间系统模型

由图1和图2，可导出VSG小信号数学模型如下式所示：

其中

式中：“Δ”代表状态变量在工作点附近的小信号扰动；kFFu为电流闭环中电压反馈系数；kFFi为电压闭环中电流反馈系数；ξ，σ分别为电流和电压控制器中积分器的状态辅助变量。下标“0”为工作点的变量值；γ为逆变器控制系统和电源相关的两个同步坐标系之间的相位差，有γ0=θVSG，0-ωgt0。

3.2 特征值分析和系统稳定性

基于式（8）中状态矩阵的特征值可分析VSG稳定性。

图3为调节a从0.5变化至50时，系统特征值在复平面中的轨迹。图3为前述传统参数整定的3种情况，但具有不同的开关频率。当系统不稳定时，特征值为黑色，图3中结果表明，当开关频率为2 kHz时，系统稳定工作范围非常窄，当开关频率增加到5 kHz时，系统稳定区间更宽，但仍对控制闭环的参数整定非常敏感。进一步将开关频率提高到10 kHz，系统具有相当宽的稳定工作范围，这意味着传统参数整定方法适用于高开关频率的低功率逆变器设计，如kW级小规模微电网应用VSG技术时。

图3 对应参数a变化的系统特性值轨迹Fig.3 The trajectories of the system eigenvalues with variation of parameter a

图3所示的特征值轨迹分析结果表明，系统稳定性受电流闭环带宽的强烈影响，即受到逆变器开关频率影响。此外，当VSG方案中采用相对较低的开关频率时，传统的参数整定方法可导致较差的动态响应性和低稳定裕度，因为各个级联控制闭环不能充分解耦。实际上，尽管各个控制闭环设计均为稳定的，但它们之间的相互作用会对系统整体稳定性产生负面影响，从而导致稳定工作范围变窄。因此，有必要探索新的参数整定方法。

3.3 参数灵敏度矩阵

定义系统极点的参数灵敏度为系统特征值对于系统参数的导数，从而可通过参数灵敏度辨识对系统临界特征值影响最大的参数，并可以揭示修改这些参数影响特征值位置的规律。

假设n阶系统具有k个可调参数，灵敏度矩阵为n×k阶。参数ρk相对于特征值λn的灵敏度αn，k可由下式表示：

式中：Ψn，ΦnT分别为与特征值λn相关联的左、右特征向量；Г为n阶系统的状态矩阵。灵敏度的实部和虚部分别与沿着实轴、虚轴的极点位置的导数相关联。由于极点位置的实部表征了系统的稳定性，故下面仅需研究灵敏度矩阵的实部。

参数灵敏度的两个例子如图4所示，系统配置见第1节中系统主要参数设置，开关频率为2 kHz，设定参数a=4。

图4 参数敏感度分析Fig.4 Parameter sensitivity analysis

图4a为参数整定导致系统失稳的情况下不稳定特征值的分布，其中深色点代表稳定特征根，浅色点代表不稳定特征根。图4b为不稳定的特征值对13个参数的灵敏度，该不稳定的特征值位置主要取决于控制器参数kpc和kpu，但LC滤波器参数和电网电感参数也有一定影响，如kpc或kpu增大，则该特征值将向左移动，从而稳定了系统。类似地，图4c、图4d绘出了接近于虚轴的另一个特征值的分析结果，图4c中浅色点代表接近于虚轴的特征值，反之则为深色点。在这种情况下，电网电感参数有显著影响，但特征值也受kiu和kd的影响。

4 VSG控制器参数整定算法

利用3.3节的灵敏度矩阵可整定系统参数。下面将引入VSG控制器的新型参数整定算法。参数整定基于一个迭代过程，其中每一步都将修改控制器参数将系统极点配置到一个更合适的位置。

图5为参数整定算法流程图。

图5 参数整定算法流程图Fig.5 Flow chart of parameter tuning algorithm

由图5可知，VSG控制器的新型参数整定算法主要步骤如下：首先，将系统参数和一组初始控制器参数配置作为迭代起点，初始参数通常是采用传统整定方法得到的。然后，计算出稳态工作点。值得注意的是，计算得到的工作点可能不稳定，但是不会影响到后续迭代过程和最终结果。接着，计算围绕该工作点的小扰动线性化系统的状态矩阵Г及其特征值。同时，辨识出具有最大实部的极点并将其选择为当前优化步骤的目标。继续计算灵敏度矩阵以得到该关键极点相对于每个可调参数的灵敏度，并找到最高灵敏度对应的参数，在每次迭代中，略微改变该参数。灵敏度的符号确定了参数是增加还是减小，以便迫使目标极点向左移动。

通常，可以根据预设的终止条件终止迭代过程。为简单起见，在该示例中，迭代过程采用固定数量的迭代。示例中整定后的参数将确保最关键的极点移动到具有较小实部的位置。尽管可以考虑更高级的改变系统参数的标准，但该算法采用简单条件通常是有益的，因为造成不稳定的极点将逐渐移动到稳定区，而极点特性将通过迫使特征值向左移动而得到改善。然而，值得注意的是，某些参数的修改可能导致其他极点右移，导致算法可能表现出在每个迭代周期的不同临界极点之间不停交替振荡。还要注意的是，可调参数不仅仅限于控制器增益，还包括物理参数如滤波电感和滤波电阻等。从这个角度来看，所提出的算法还可用于系统设计早期阶段。

5 仿真验证

图6 参数整定过程Fig.6 Parameter tuning process

对图1、图2所示的逆变器及其VSG控制器进行了基于迭代算法的参数整定，并将参数设置后的系统性能与传统参数设计进行对比，从而验证新型算法的效果。其中可调参数集设为7个参数，即kpc，kpu，kic，kiu，ωf，pu，mq和kd，因为考虑主回路参数已固定。图6a、图6b为随着迭代过程参数改变导致的系统极点位置变化，从图中可以看出，由于极点向左偏移，系统动态响应更快，同时稳定裕度更大。图6c、图6d给出了迭代运算中参数kpc和kpu具体的优化过程。由图6中可看出，电流闭环控制器的增益kpc在前约1 500次迭代中保持不变，但电压闭环控制器的增益kpu增加，随后kpu在约2 500次迭代中保持不变，而kpc持续增加。

选择2 500次迭代后得到的参数集合作为最终结果，以避免过高的电流控制器增益。将这些参数在系统中设定后与传统参数整定（a=3）得到的系统性能进行时域仿真对比，工作点选择一致，然后比对功率参考阶跃后的系统动态响应。图7、图8分别为使用传统参数整定方法和新型参数整定方法得到系统动态响应结果，其中Δ|uO|为输出电压动态扰动值，Δ|iO|为输出电流动态扰动值，Δωpu为VSG转速动态扰动值。对比图7、图8可看出，系统稳态输出是一致的，两种时域仿真都产生了稳定的系统动态和足够的阻尼振荡，但是，图8的动态响应速度明显更快。同时，如前所述，传统参数整定方案得到系统稳定区较小，故对干扰、参数不匹配、工作点变化更为敏感。而利用所提出的算法获得的参数集可得到更稳定的系统运行条件。