基于扰动抑制的三相逆变器模型预测控制策略
2021-01-21张薇琳陈灵敏
张薇琳,陈灵敏
(1.广东交通职业技术学院轨道交通学院,广东 广州 510650;2.广东工业大学试验教学部,广东 广州 510006)
三相逆变器广泛应用于不间断电源、储能系统和分布式发电系统中[1]。通常,三相逆变器在电压源模式下运行时的控制目标是:能够提供高质量的正弦电能,即动态响应快速、稳态误差小和总谐波失真(total harmonic distortion,THD)低[2]。
目前,三相逆变器的控制策略包括:比例积分控制[3]、最优控制[4]、自适应控制[5]、重复控制[6]、滑模控制[7]、无差拍控制[8]和模型预测控制(model predictive control,MPC)[9-15]等。比例积分控制属于线性控制,结构简单,但需进行较好的参数整定以优化闭环性能,同时在违反输入约束或不确定参数情况下难以保证稳定性。最优控制可基于指标约束优化闭环控制性能,但在处理非线性因素时难度较大。自适应控制和重复控制在处理诸如负载波动和参数变化等系统扰动中非常有效,然而这两种方法计算复杂,且控制增益选择上难度较大。滑模控制可有效处理有界参数变化问题,但切换结构可能带来降低输出电能质量的抖振问题。无差拍控制提供了非常好的动态响应,但对干扰或参数不匹配较敏感,鲁棒性一般。
通常,用于电力电子设备的MPC控制器可分为两种:连续控制集MPC控制器[9-10]和有限控制集MPC控制器[11-15]。连续控制集MPC方法中,控制输入被视为有界连续变量,MPC可为调制器实现离线优化。然而,复杂约束或模型非线性将使得优化过程困难,甚至可能无有效解。有限控制集MPC控制器则是利用有限开关矢量来处理优化问题。由于控制集的元素数量有限,故计算负担不大,从而MPC控制器可在线实现。有限控制集MPC控制器的最大优势是快速的动态响应和灵活的目标约束[11]。然而,其也会导致可变的开关频率、高采样频率和高纹波输出,故有文献改进了预测方式试图降低MPC控制器带来的不利影响[12-13],但牺牲了预测精度。文献[14]结合传统调制策略设计了固定开关频率的MPC控制器,但存在计算负担重的问题。同时,MPC控制器的稳定性分析难度也较大[15]。
根据前述研究,本文提出了一种基于扰动抑制的MPC控制器,其具有无约束和有约束两种模式,分别对应处理动态和稳态。MPC控制器基于离散时间扰动观测器(disturbance observer,DOB)对预测模型进行了优化,可补偿模型不确定性。同时,基于Lyapunov函数分析了MPC控制器的稳定性。最后,采用实验验证了新型MPC控制器的性能。
1 三相逆变器的预测模型
三相逆变器前端为直流电源,三相桥臂输出经由LC滤波器至三相负载,如图1所示。基于扰动抑制控制法可推导三相逆变器的离散时间状态空间数学模型。
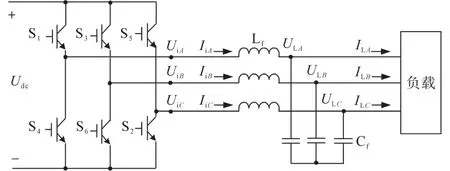
图1 三相逆变器电路图Fig.1 Diagram of the three-phase inverter circuit
图1中,逆变器三相桥臂输出线电压矢量Uiabc=[UiAUiBUiC]T,逆变器三相桥臂输出相电流矢量Iiabc=[IiAIiBIiC]T,负载线电压矢量ULabc=[ULAULBULC]T,负载相电流矢量ILabc=[ILAILBILC]T。
使用前向欧拉方法得到离散化的基于d-q同步参考坐标系的逆变器模型:
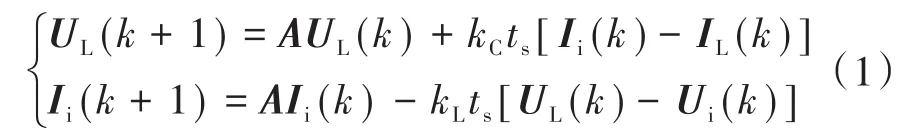
其中

式中:ω为电角频率;ts为采样周期;Cf,Lf为滤波电容和电感;Ui(k)为逆变器电压矢量,即控制输入;UL(k)为负载电压矢量,即受控输出;Ii(k)为逆变器电流矢量,即状态变量;IL(k)为负载电流矢量,即未知干扰。k为离散时间域中的第k个采样时刻。
在后续描述中为了简化,不再附加k,因为始终在离散域中分析,对于k+1时刻则采用上标“+”表示。此外,上标“*”表示参考值。
通常,MPC控制器中预测模型可由式(1)实现。然而,为了使用Lyapunov函数证明系统稳定性并且利用基于误差模型预测的优点,需导出误差动态模型。首先,式(1)的平衡状态定义为:,式(1)所描述的数学模型的状态变量没有变化。因此,平衡状态下的逆变器电流和控制输入为
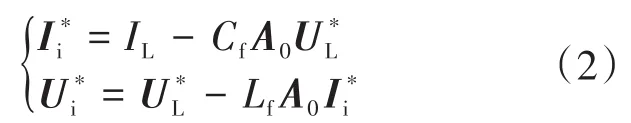
其中
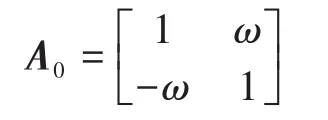
然后,引入以下误差矢量来推导误差动态模型:

式中:ULe为负载线电压误差矢量;Iie为输出相电压误差矢量;Uie为输出线电压误差矢量。
将式(3)代入式(1)可得到误差动态模型:

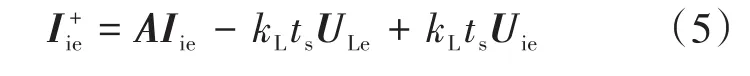
式(4)和式(5)构成了一个单输入矢量Uie∈R2×1和单输出矢量ULe∈R2×1的二阶系统。为简单起见,采用矩阵描述如下:
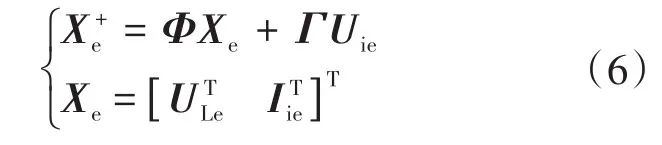
其中
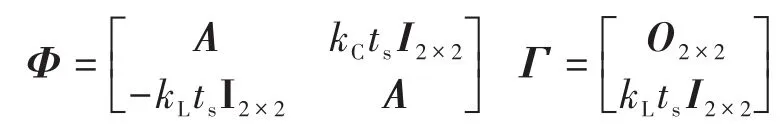
式中:Im×n和Om×n分别为m行n列的单位矩阵和零矩阵。
式(5)代入式(4)后可得两步超前预测如下:

其中

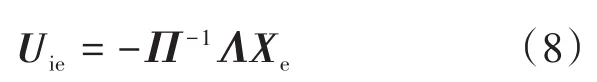
2 MPC控制器的无约束模式设计
总扰动估计方法的优点是可以基于系统动态来简化模型。值得注意的是,电压参考U*L是已知的,同时在小采样周期下,负载电流IL与状态变量动态相比,变化更缓慢。此外,式(2)中的平衡变量在较小的采样周期内变化也很慢,即,然后组合误差动态模型式(4)和式(5)可导出DOB的增强动态模型如下:
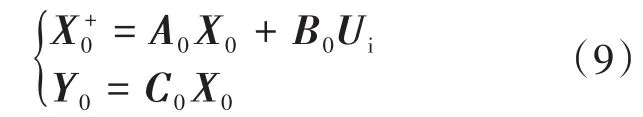
其中
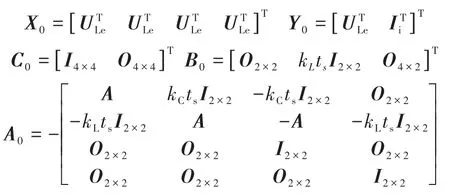
进一步,DOB可表示如下:
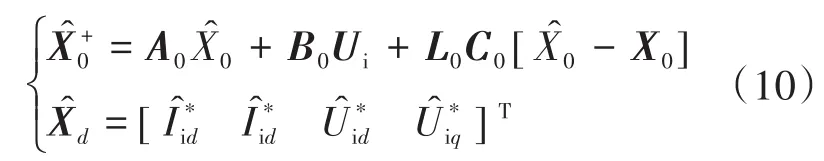
式中:上标“^”表示估计值;L0为观测器增益矩阵,L0∈R8×4。
联立式(9)和式(10)可得到的DOB的误差动态如下式:
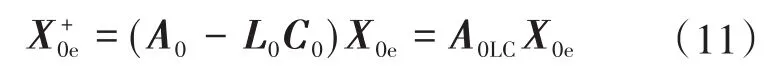
其中
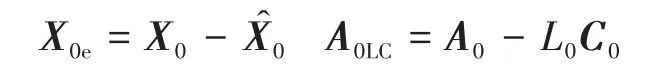
可通过下式计算优化增益矩阵:
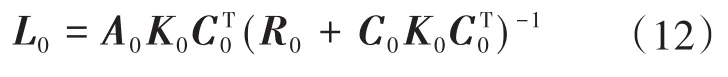
式中:K0为离散时间代数Riccati方程的解,K0∈R8×8,如下所示:
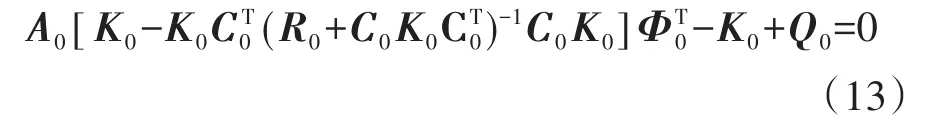
式中:Q0为对称正半定矩阵,Q0∈R8×8;R0为对称正定矩阵,R0∈R4×4,0是考虑设计参数高斯白噪声的协方差矩阵。
注意,这些设计参数被简化为Q0=λR0,其中λ为比例系数,是一个正实数。
选择Lyapunov函数如下:
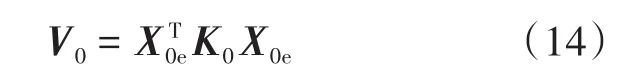
对Lyapunov函数进行稳定性判定如下:

式(15)证明了AA0LC是稳定的矩阵,XX0e是指数稳定的。
图2为基于DOB的MPC控制器框图。
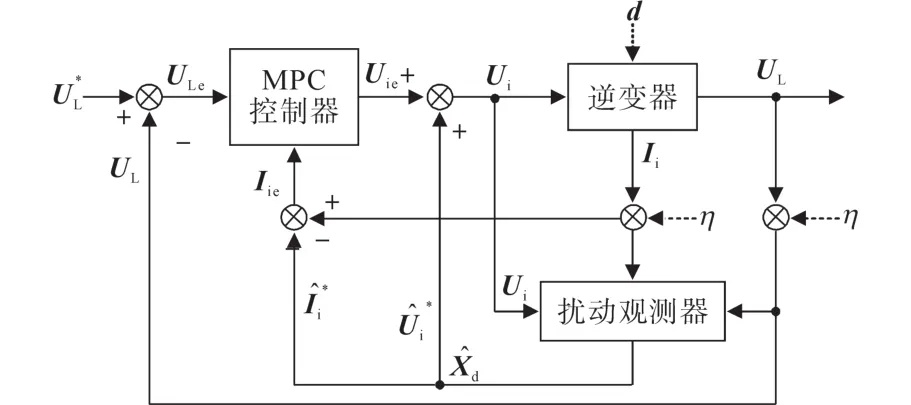
图2 基于DOB的MPC控制器框图Fig.2 Block diagram of MPC controller based on DOB
图2中,d和η分别为过程干扰和测量噪声,图中所示,通过I*i和U*i补偿模型和输入控制后,一旦DOB观测到干扰,控制器就可以拒绝这些对系统的扰动而实现稳定运行,而与运行模式无关。因此,DOB既观测扰动,又可处理噪声。补偿模型如下式:
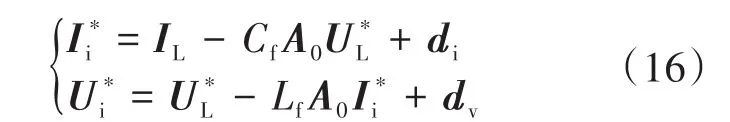
式中:di,dv为其他过程扰动。
由式(12)和式(13)给出的基于Kalman-Bucy滤波的观测器稳态增益依赖于两个协方差矩阵Q0和R0表示的噪声统计条件概率。基于DOB的预测可利用合适的协方差矩阵来提高所提出的MPC控制器的抗噪性。
MPC控制器源于下述成本函数的优化问题:
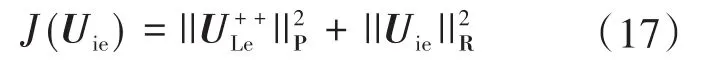
式中:P∈R2×2和R∈R2×2是正定加权矩阵;||.||2P=(.)TP(.)为二次型。
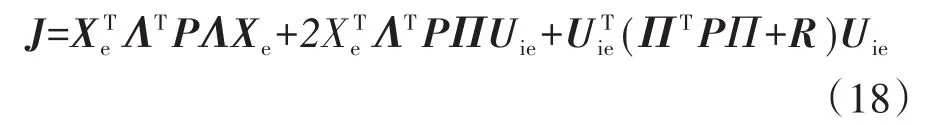
对式(18)求偏导可得全局最优解:

式(19)给出了一个线性反馈最优控制律,其最佳增益为

因此,基于扰动抑制的最优控制律可表示为
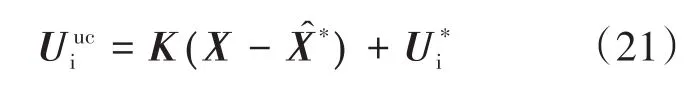
下式为求解加权矩阵P的方程:
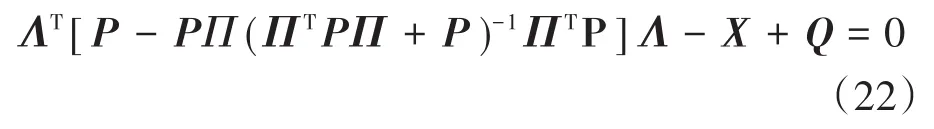
其中
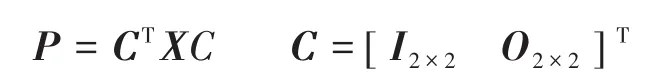
通过选择加权矩阵P为式(21)的解,则控制律式(21)变为的线性二次型(linear quadratic regulator,LQR)控制器,将使成本函数最小化,成本函数最小化公式为

从而所提出的方法可通过在设计中适当地调整P和R来实现成本函数的灵活性。
无约束模式定义为不违反空间矢量调制(space vector modulation,SVM)确定的输入约束的模式。图2中的MPC控制器即是处于无约束模式,因为其满足约束如下:
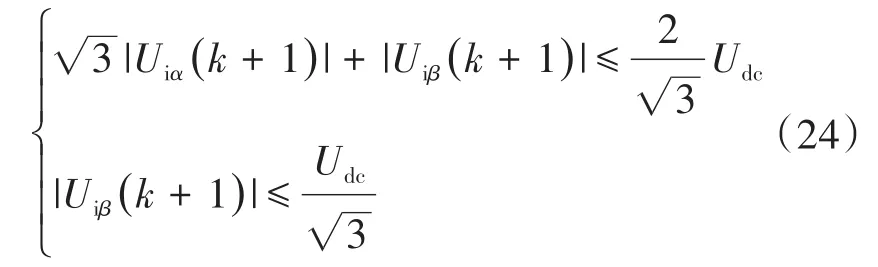
式中:Uiα,Uiβ为静止α-β坐标系中的控制输入。
以上约束是SVM六边形边界确定的,在实际中,通常是采用了六边形内圆简化式(24)中的约束。无约束模式下的MPC控制器可精确调节稳态输出电压,其中式(21)的最优控制输入直接通过标准的SVM模块生成控制脉冲。
3 MPC控制器的约束模式设计
当违反输入约束式(24)时,通过利用无约束解式(21)和SVM的切换,可设计MPC控制器的约束模式。MPC控制器的约束模式主要用于处理快速动态。
图3为基于扇区的SVM开关矢量合成示意图。
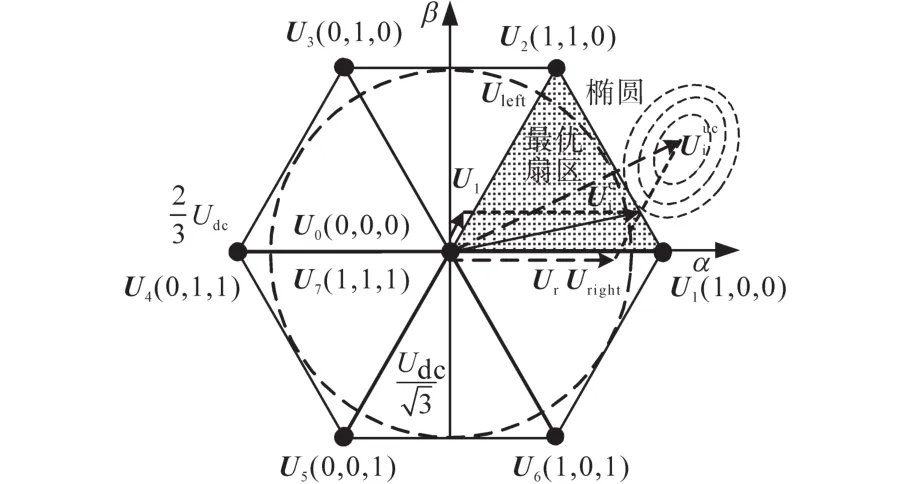
图3 基于扇区的SVM矢量合成Fig.3 Sector-based vector synthesis of an SVM
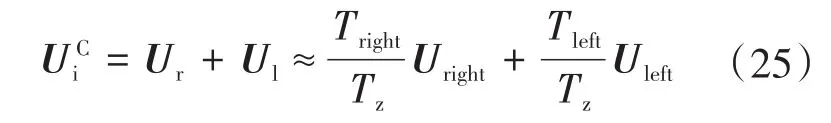
其中
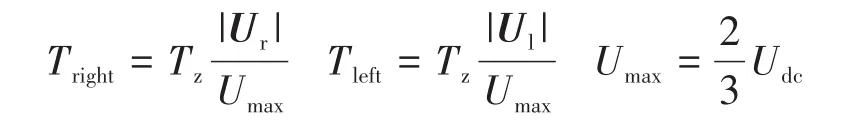
式中:Tz为调制周期。
在约束模式中,仅使用有效基本矢量来获得参考矢量,即使用传统SVM中相邻基本矢量Uright和Uleft分别在作用时间Tright和Tleft来近似,不再使用零矢量,同时不考虑Tz内的系统动态。在图3中,Tz内关联最优扇区得到开关序列由˜=[Ui0,Ui1,…,UiN-1]=[Uright,Uright,…,Uleft,Uleft]表示,其中N为预测范围。开关序列中(Uright,Uleft)保持1个采样周期ts,故N=Tz/ts,并且在每个Tz中,对于开关序列存在N+1个可能的选项。
图4给出了所提出的基于SVM的约束模式MPC控制器的有限开关序列,其中N=6。在图4中,从Uright至Uleft的切换瞬间,控制序列有7个选项(N*=0,1,2,…,6)。然后,对于每个控制序列,从初始状态Xe开始到最终状态XeN,可使用式(6)递归预测,如下所示:
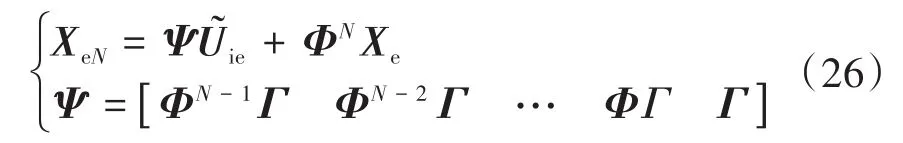
从而约束模式下的MPC控制器优化问题为
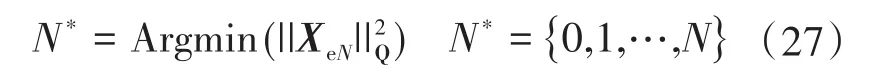
式(27)可解释为在N+1个选项内找到最优N*。为了求解式(27),所有开关序列可基于有限控制集MPC方式评估得到最优解。基于预测模型式(26)可采用不同的非线性模型和不同的离散方法,如显式前向欧拉法。本文即采用前向欧拉法,主要考虑到在短时预测背景下,其计算简单,且精度可接受。综上,含两种运行模式的新型MPC控制器设计完成,与其他MPC方法不同,其利用SVM简化了最优开关序列求解,同时还固定了开关频率。
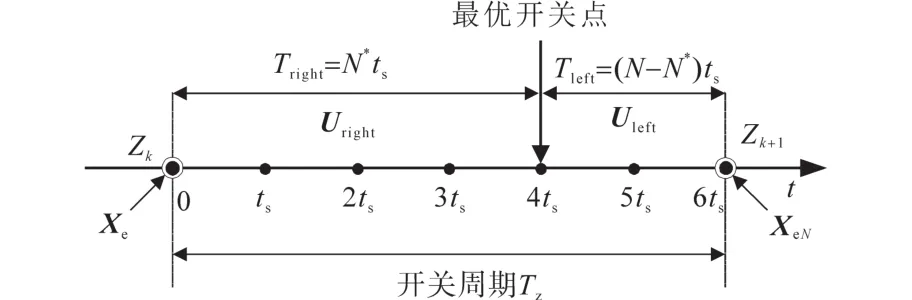
图4 N=6时约束模式下的有限开关序列Fig.4 Finite switching sequences in constrained mode with N=6
4 MPC控制器稳定性分析
使用Lyapunov稳定性理论证明了无约束模式下MPC控制器的稳定性。由估计扰动重写式(21)如下:
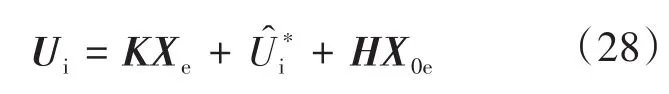
其中
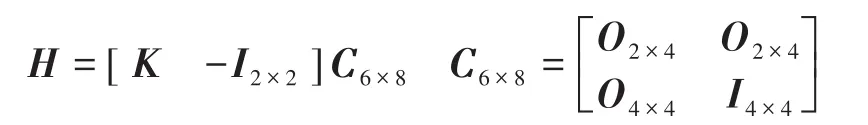
选择Lyapunov函数为
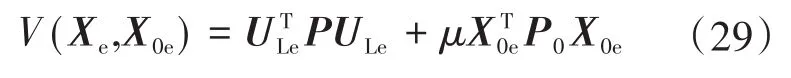
对Lyapunov函数进行稳定性判定如下:
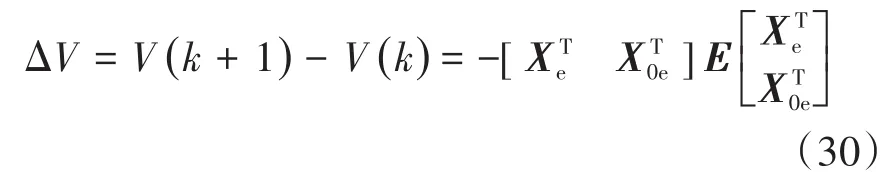
其中
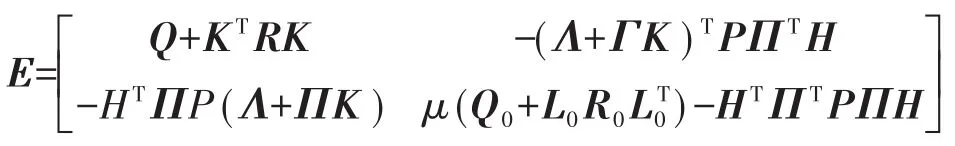
令
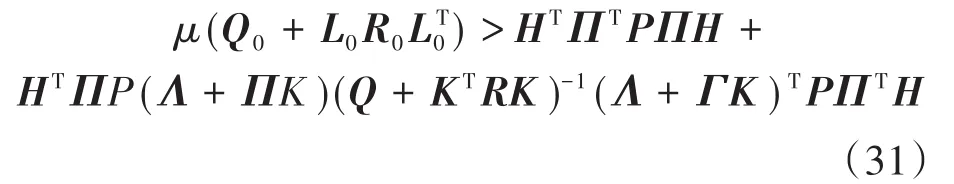
式中:μ为一个标量系数。
式(30)中ΔV<0(仅在期望的平衡状态下ΔV=0)对应的μ足够大。至此,证明了所提出的基于DOB的MPC控制系统的渐近稳定性。
5 实验验证
为了验证所设计的控制策略,搭建了如图5所示的实验平台。实验系统主要参数为:额定容量Sn=4 kV·A,直流电压Udc=570 V,LC滤波器滤波电容Cf=6.6µF,滤波电感Lf=10 mH,开关频率fsw=5 kHz,采样频率fs=20 kHz,约束模式参数N=20/5=4,输出频率f1=50 Hz,额定输出电压UL,rms=220 V。

图5 三相逆变器实验平台Fig.5 Experimental platform of the three-phase inverter
本文设计了3组实验,包括动态性能实验、鲁棒性实验和负载阶跃实验。
实验采用新型MPC控制器和LQR控制器对比的方式进行。选择LQR控制器是因为其是一种完善的控制方法,具有明确的性能指标定义。为了公平对比,成本函数、采样频率、开关频率、工况和LC参数均相同。为了减少在线计算负担,预先离线计算了式(20)中反馈增益矩阵K和式(26)中常数矩阵Ψ和Φ。
5.1 动态性能实验
MPC控制器动态响应与式(17)中成本函数和加权重矩阵Q和R相关。考虑到式(17)中U++Le和Uie具有相同的单位和等效维度,故选择为P=I2×2和R=εI2×2,其中加权因子ε是正实数。利用ε可简化加权矩阵设置。在约束模式中,期望快速的动态响应,因此选择ε为小值,而在无约束模式下,需要达到较好的稳态性能,故调整ε为大值。值得注意的是,新型MPC控制器允许在两个模式中独立选择Q和R以避免LQR控制器中Q和R的折衷。
图6为当参考输出电压U*Ld在逆变器空载下阶跃变化时传统LQR控制器和新型MPC控制器的动态性能实验结果。
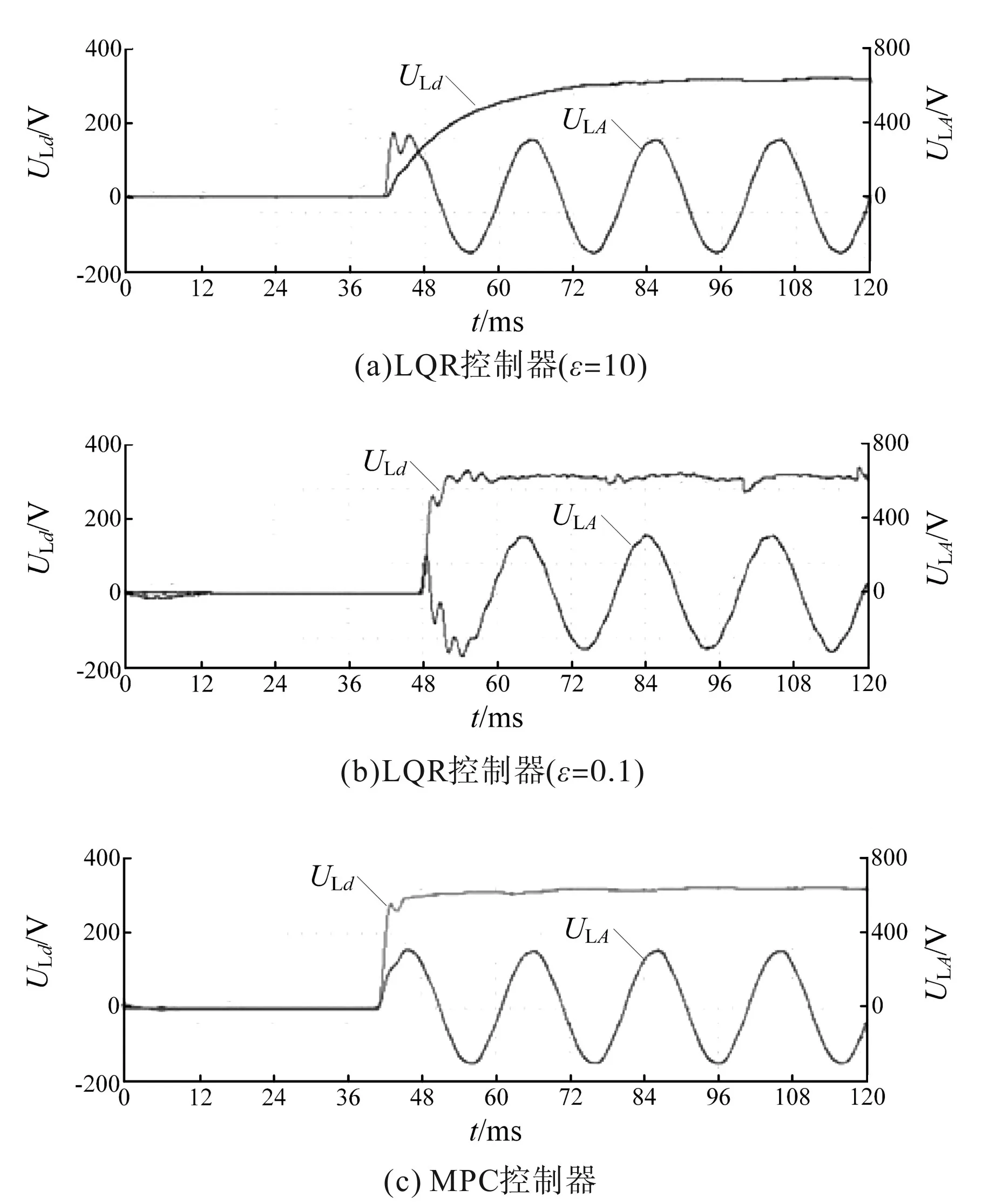
图6 LQR与MPC控制器动态性能对比Fig.6 Dynamic performance comparison between LQR and MPC controller
图6a为传统LQR控制器设置ε=10的实验波形,ULd上升时间为25 ms,稳定后ULA的THD为0.70%,对应图6b为传统LQR控制器设置ε=0.1的实验波形,上升时间降低至2 ms,但THD增加至1.6%,故传统LQR控制器需在动态和稳态期望性能之间权衡。图6c为所提出的MPC控制器的实验波形,上升时间为1.8 ms,同时THD只有0.65%,这说明了其无需折衷动态和稳态期望性能的优越性。
5.2 控制器鲁棒性分析
在负载阶跃变化条件下,进行评估基于扰动抑制的MPC控制器对参数误差的鲁棒性性能的实验。
将滤波电感和电容参数设置为标称值的2倍(Lf=20 mH,Cf=13.2µF),图7为采用传统LQR控制器和新型MPC控制器的实验结果对比。从图7中可以看出,LQR控制器出现了19 V(6.1%)的稳态电压误差,而MPC控制器只有1 V(0.6%)的稳态电压误差。同时,A相电压的THD分别为0.75%和0.65%。

图7 LQR与MPC控制器鲁棒性对比Fig.7 Robust comparison between LQR and MPC controller
5.3 负载阶跃变化实验
图8和图9为线性负载阶跃变化下LQR和MPC控制器的测试结果波形图。由图8、图9可知,LQR控制器作用下的稳态电压误差为1.6 V,THD为0.75%,负载阶跃变化对应的恢复时间为6.5 ms;而MPC控制器作用下的稳态电压误差为0.6 V,THD为0.7%,负载阶跃变化对应的恢复时间为2.8 ms,同时,对比LQR控制器,MPC控制下的逆变器输出电压在负载阶跃变化时的电压尖峰和跌落都更小。
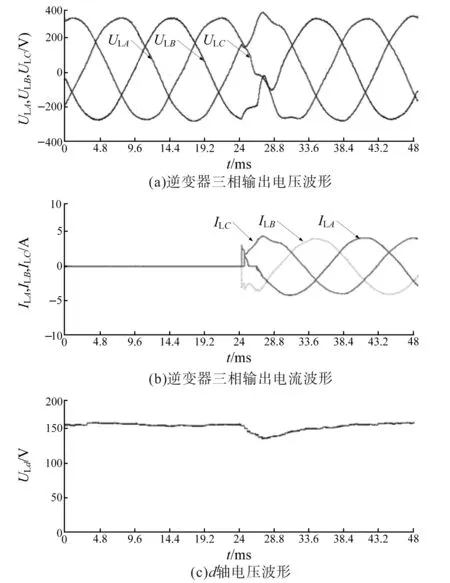
图8 线性负载阶跃下的LQR控制器实验结果Fig.8 Test results of LQR controller with linear load step
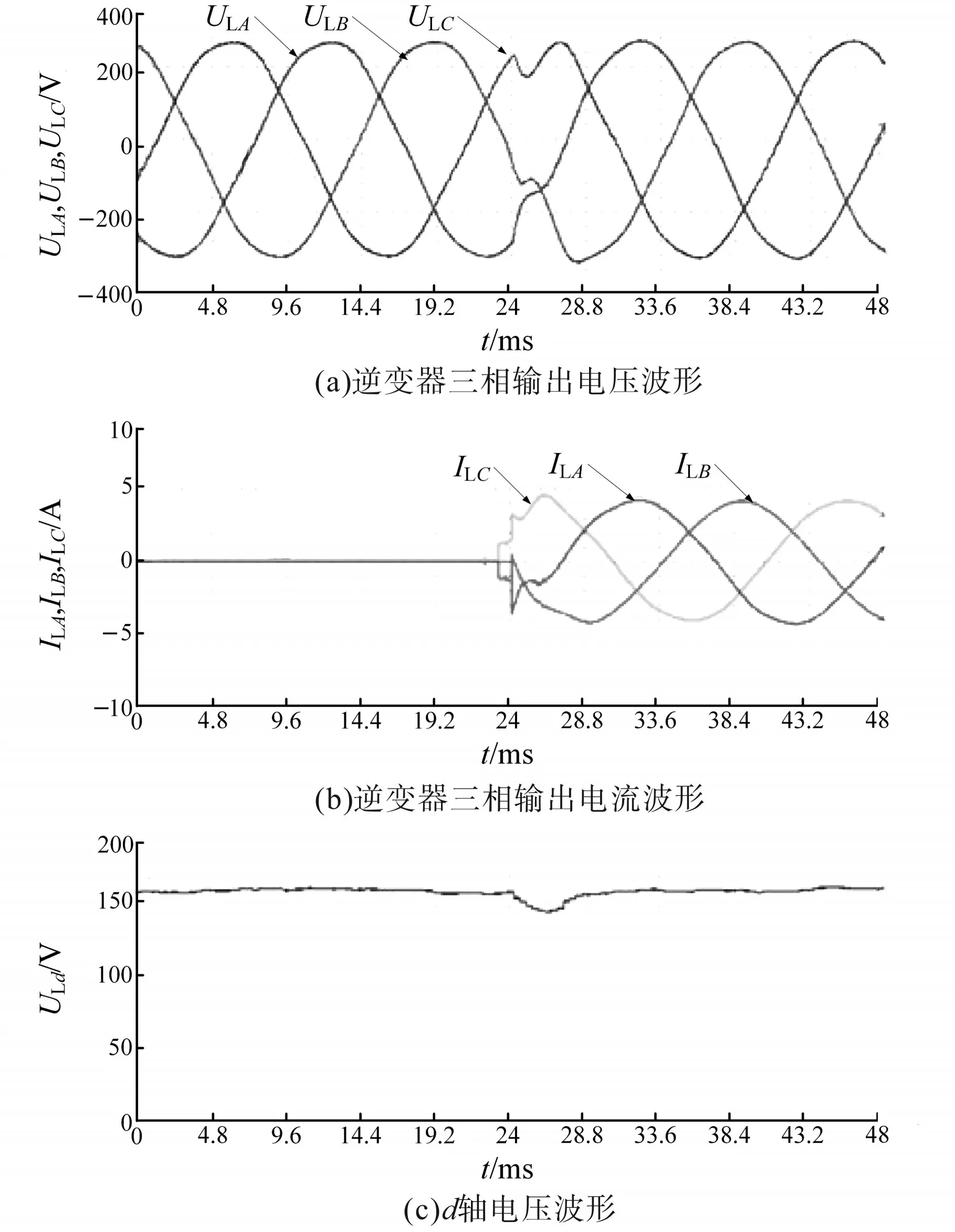
图9 线性负载阶跃下的MPC控制器实验结果Fig.9 Test results of MPC controller with linear load step
图10、图11分别为非线性负载阶跃变化下LQR和MPC控制器的控制实验结果波形图。

图10 非线性负载阶跃下的LQR控制器实验结果Fig.10 Test results of LQR controller with nonlinear load step
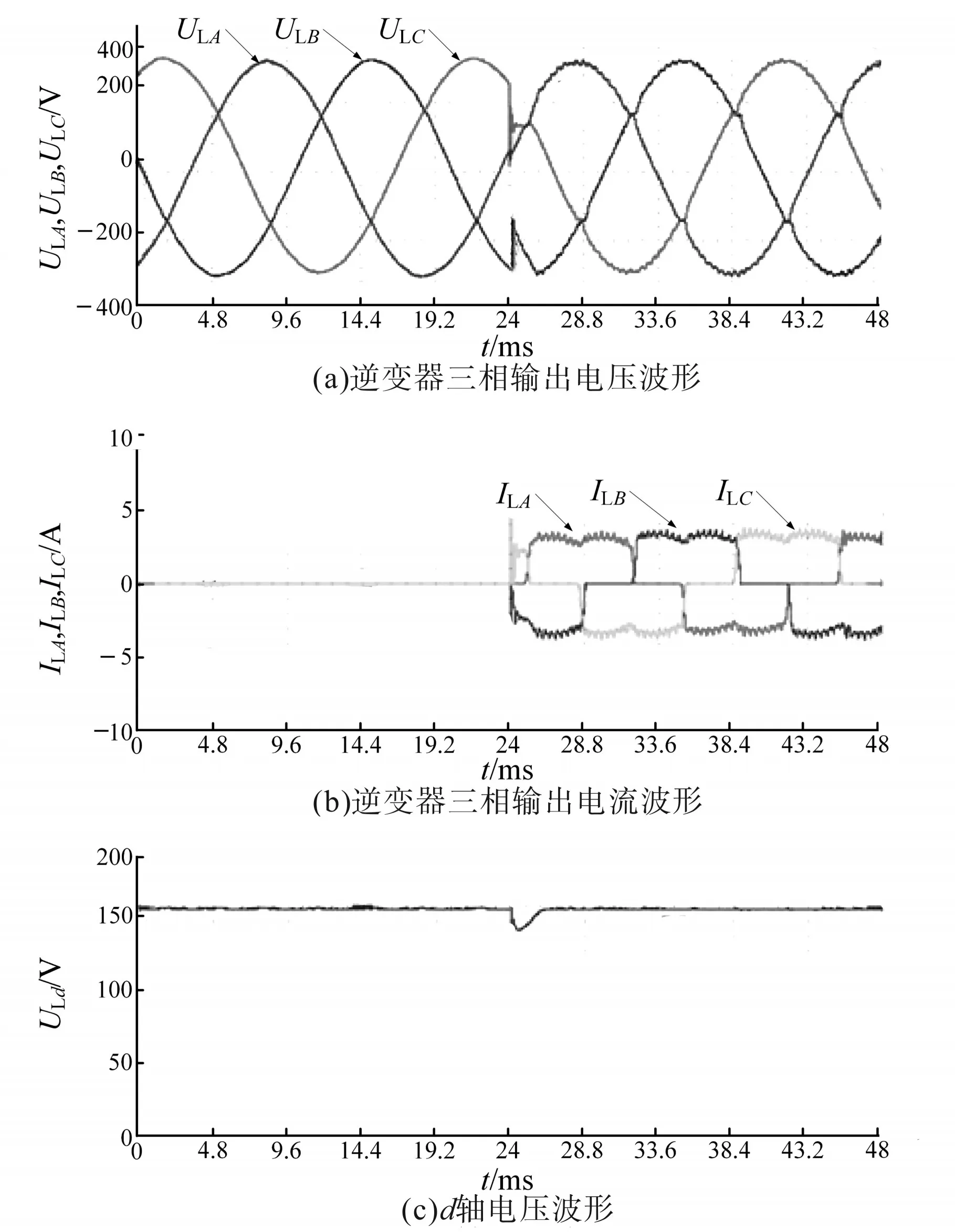
图11 非线性负载阶跃下的MPC控制器实验结果Fig.11 Test results of MPC controller with nonlinear load step
从图10、图11中可以看出,非线性负载阶跃变化下,LQR控制器对应的电压恢复时间为4.8 ms,其电压跌落为184 V,稳态电压误差为3 V,THD为2.6%,而新型MPC控制器作用下,恢复时间降低至1.8 ms,电压跌落为96 V,稳态电压误差为0.5 V,THD为1.4%。
6 结论
围绕对三相逆变器的控制性能提高,提出了一种基于扰动抑制的三相逆变器灵活模式设置MPC控制器。
基于DOB对MPC控制器中的预测模型进行了简化,并设计了无约束和有约束两种模式,在提高系统动态性能的同时保持了较好的稳态输出性能。
基于Lyapunov函数证明了新型MPC控制器的稳定性。
对比实验结果说明,与传统LQR控制器相比,所提出的MPC方法在稳态和动态中都表现出了更好的控制性能。
