颗粒形状对粗粒土剪切变形影响的细观研究

魏 婕，魏玉峰，黄 鑫

（成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059）

粗粒土作为一种颗粒状无黏性土广泛存在于自然界中，力学性质极其复杂，其抗剪强度主要源于颗粒间的滑动摩擦强度和咬合摩擦强度两部分，而颗粒形状又影响着咬合摩擦强度，因此对粗粒土颗粒形状的研究至关重要。近年来，国内外众多学者从颗粒级配、孔隙比、颗粒破碎等方面对粗粒土的抗剪强度、变形特性、渗流性能等角度取得了丰富的研究成果[1-8]，发现颗粒形状是影响粗粒土密实度、力学与渗流等特性的主要因素之一[9-13]。杨贵等[10]采用水泥净浆浇筑方法，制备了相同体积不同形状的粗颗粒近似模拟堆石料颗粒，通过三轴剪切试验发现：随着颗粒球度的增大，人工模拟堆石料峰值强度增大，内摩擦角增量随着颗粒球度的增大而减小。何亮等[14]认为粗粒土颗粒随圆度减小，更易在颗粒边界棱角处产生微裂纹使颗粒磨损，且同一类型颗粒法向应力增大，达到损伤临界状态圆度损伤所需能量增大，圆度损伤因子减小。J.S.Dodds[15]、刘秉清等[16]的研究结果表明，颗粒形状等微观参数对砂土力学性质的影响较大。史旦达[17]基于PFC2D离散元软件，采用“clump”构造了“椭圆团颗粒”，研究了颗粒形状对砂土抗剪强度和变形特性的影响。孔亮等[18]用 PFC2D模拟颗粒堆积试验、双轴试验和直剪试验，探讨了颗粒形状对类砂土材料宏观力学特性的影响规律。张翀等[19]在研究中发现颗粒形状对颗粒试样的宏观特性有较大的影响，异形颗粒由于颗粒形状的特殊性，显著地提高了颗粒试样的剪切强度。任树林等[20]发现异形颗粒间的咬合自锁作用大于圆形颗粒，致使异形颗粒填充的断层破碎带摩擦强度高于圆形颗粒填充的断层破碎带摩擦强度。

本文通过PFC2D颗粒流程序对不同形状的粗粒土试样进行直剪数值模拟。选定特定状态对试样直剪过程中的宏细观力学特性进行分析，主要对不同颗粒形状粗粒土试样在剪切过程中的剪切带厚度、颗粒旋转量值、平均接触数、孔隙率增量及接触力系等宏细观参量的演化规律进行研究，进而揭示出颗粒形状对粗粒土剪切影响的深层内在机理。

1 粗粒土直剪试验方案及结果

1.1 颗粒形状参数与试样参数的选定

按照孔亮等[18]提出的形状系数法来量化颗粒形状，其计算公式为：

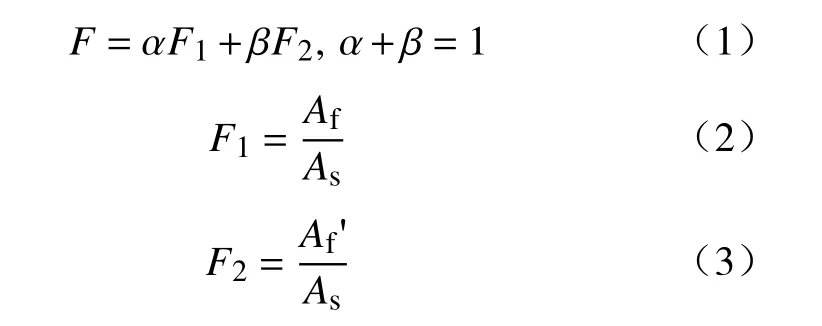
式中：F-形状系数；

F1-圆形度；

F2-凹凸度；

α、β-F1、F2的权重系数；

Af-颗粒面积；

Af'-颗粒最大内接标准椭圆面积；

As-与颗粒周长相同的圆面积。

取α=β=0.5，即形状系数为二者的平均值。根据面积等效、质量等效和质心不变等原则[21]，采用clump单元，建立如图1所示的4种试样颗粒。初始构建模型时，颗粒试样的方位角范围在0°～360°内随机分布，进而分析颗粒形状对粗粒土剪切力学特性的影响。依据公式（1）、（2）和（3），得到图1四种不同形状颗粒参数的F1，F2和F（表1）。

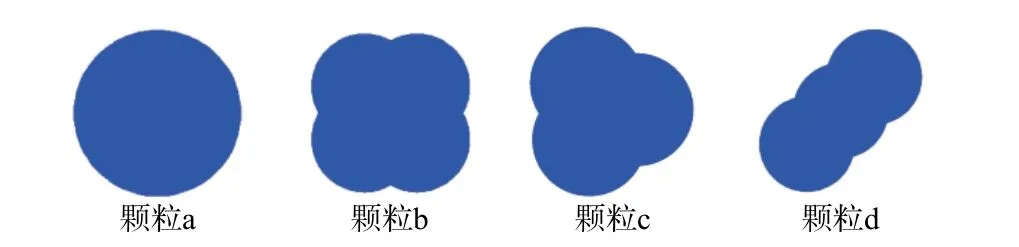
图1 试样颗粒Fig.1 Sample particle

表1 形状参数统计表Table1 Statistics of the shape coefficients

本文的数值试验采用ball 及clump 构建4种不同形状的粗粒土颗粒，黏聚力按零考虑，颗粒间接触采用线性接触刚度模型。数值试验剪切盒的尺寸为200 mm×200 mm，颗粒粒径范围为2～20 mm，本文不考虑级配的影响，因此异形颗粒的级配与初始纯圆颗粒级配一致。主要细观参数有颗粒间的接触刚度、墙体的接触刚度、粒间摩擦系数、初始孔隙率及密度等，根据J.Wang[22]及蒋明镜等[23]所采用的数值试验参数并进行了适当调整，具体取值情况见表2。颗粒试样生成后，对颗粒间的接触应力进行初始化，再对模型进行伺服控制，固定下剪切盒，再保持法向应力恒定的条件下，对上剪切盒施加一个水平向右的速度进行剪切，颗粒a的初始数值模型如图2所示。

表2 模型细观参数Table2 Mesoscopic parameters of the model

图2 颗粒a 初始模型结构图Fig.2 Structure diagram of the initial model of particle a

1.2 颗粒形状对粗粒土剪切特性的影响分析

1.2.1 直剪试验参数验证

为了验证数值试验参数的可靠性，本文室内物理试验选用a型颗粒与数值试验的结果作对比分析。试验仪器使用的是可视化中型直剪仪，主要由反力基座（可拆卸式外框架）、应力加载系统、滑动装置、可观测式剪切盒、数据采集系统组成。根据土工试验规程规定，为满足试验要求本文试验选用颗粒粒径范围在2～20 mm的圆形颗粒。剪切过程中分别施加100 kPa，200 kPa和300 kPa的法向应力。

图3为不同正应力条件下颗粒a 物理试验与数值试验的剪应力-剪切位移对比曲线。由图3可知，数值试验与物理试验剪切过程中的剪应力-剪切位移曲线的变化趋势较为一致，剪切过程中表现为先增加后达到残余强度。

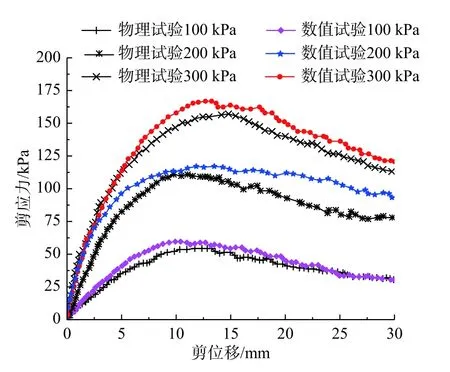
图3 颗粒a 室内试验与数值试验结果对比图Fig.3 Comparison chart of the numerical test and indoor test results of the particle a

1.2.2 颗粒形状对粗粒土剪切特性的影响

考虑到粗粒土颗粒在高正应力下可能发生破碎，本文以200 kPa 下的试验结果来分析不同形状颗粒在剪切过程中表现出的剪切特性的异同。图4、图5分别为200 kPa 法向应力下四种颗粒的剪应力-剪切位移曲线和剪位移-体应变曲线（图中体积应变坐标轴，体积压缩为负，体积膨胀为正），图中表明：在颗粒形状的影响下，粗粒土试样颗粒在正应力一定条件下均表现出一定的应变软化和先轻微剪缩再大幅度剪胀特性。

由图4可知，随着形状系数F减小，粗粒土峰值剪应力增大，即在相同粒级、颗粒级配的情况下，颗粒轮廓形状越复杂，颗粒之间的咬合及摩阻力也越大，其抗剪强度也就越高。由图5可知，在加压初期，F=0.720试样产生体积剪缩效应最明显，而纯圆颗粒的剪缩幅度最小。持续加压时，4种颗粒均大幅剪胀，异形颗粒剪胀幅度明显大于纯圆颗粒。

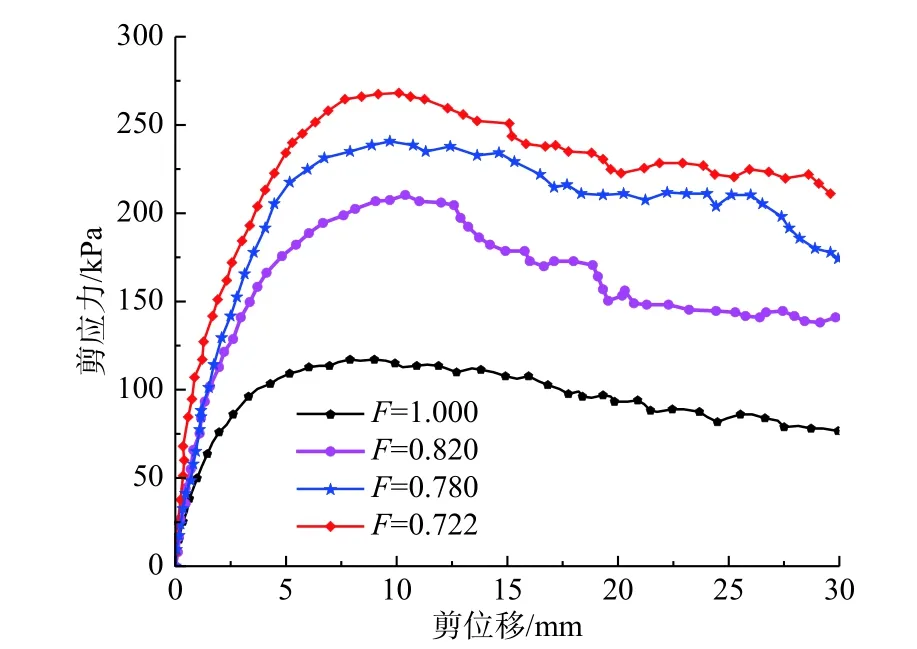
图4 不同形状系数试样的剪应力-剪切位移关系曲线Fig.4 Shear stress-shear displacement curve of specimens with different shape coefficients

图5 不同形状系数试样的体应变-剪切位移曲线Fig.5 Volume strain-shear displacement curves of specimens with different shape coefficients

剪切过程中，颗粒实际上受到的合力方向是非水平的，若将实际合力当作轴向应力，将剪切盒的约束力当作围压，剪切带内的颗粒受力情况与三轴试验的受力形式十分类似。在三轴试验中，围压的大小决定了试样破坏时的峰值强度，而围压就起到了限制试样剪胀的作用，因此粗粒土的剪胀幅度是影响其抗剪强度的主要因素。

M.Oda 等[24]指出颗粒试样的体积变化主要反映在剪切带区域，且剪切带内力链的崩溃主要由滚动引起。通过观察剪切过程中剪切带内颗粒位置的变化情况，将剪切位移为10 mm时的4种颗粒剪切带的形状绘于同一图中，根据剪切盒的尺寸计算得出各自的剪切带宽度（图6）。剪切时颗粒形状变化对剪切带厚度有一定影响，表现为变形的局部化发生在狭长的剪切带内，且上下剪切盒内的颗粒运动幅度不相同，上剪切盒位移较大。分析图6，随着F的减小，剪切带厚度增大，当F=1.000，0.820，0.780，0.722时，所对应的剪切带厚度分别为38.2 mm，41.8 mm，43.5 mm和44.7 mm，纯圆颗粒剪切带内的剪胀幅度不如异形颗粒。

对试验过程中试样不同高度范围内颗粒的旋转角度进行统计，得到图7所示旋转角度与试样高度的对应关系。剪切带内颗粒平均旋转量较大，向两侧逐渐减小。另外，纯圆与异形颗粒的峰值旋转角度相差较大，形状系数F越小，颗粒平均旋转量越小。纯圆颗粒旋转角度最大可达67.8°，且随着F的减小，峰值旋转角度减小。说明在相同外力作用下，纯圆颗粒试样在剪切过程中的旋转幅度更大，其结构稳定性较差。

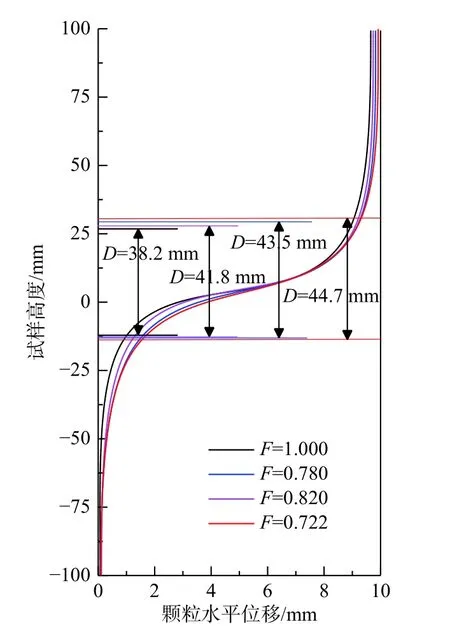
图6 剪切带厚度Fig.6 Shear zone thickness

图7 颗粒旋转量值Fig.7 Particle rotation value

1.3 颗粒形状对粗粒土剪切变形影响的力学机理

剪切过程中，颗粒主要以滑动和滚动两种方式运动，粗粒土的抗剪强度主要由两方面组成：颗粒间的滑动摩擦强度和咬合摩擦强度。在外力作用下，颗粒发生相对运动，导致颗粒重新定向排列。试样颗粒越光滑，其颗粒间的咬合嵌锁作用越弱，咬合摩擦强度越小，其抗剪强度主要体现为滑动摩擦强度；而试样颗粒表面若有起伏，颗粒间则存在较强的咬合嵌锁作用，且颗粒表面越粗糙，其咬合嵌锁作用越强。

图8为考虑滚动阻矩的圆形颗粒和形状系数F=0.820、F=0.780的clump颗粒在平面上滚动的示意图。分别在两种颗粒的质心上作用水平力T来推动颗粒滚动，同时在质心上作用一个垂直力Fn[25]。

图8 异形颗粒等效滚动示意图[25]Fig.8 Schematic diagram showing equivalent rolling of irregularly shaped particles [25])

根据Iwashita 等[26]的研究，采用Mr来定义抗滚动模型中的滚动阻矩，其表达式为：

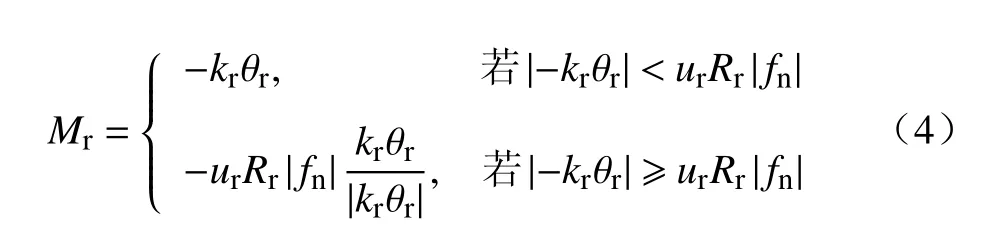
式中：kr-滚动刚度，Iwashita 等[26]建议其取值为

ks-颗粒切向刚度；

ur-滚动摩擦系数；

fn-颗粒间法向接触力；

Rr-两颗粒的共有半径，

滚动摩擦系数的取值可根据Estrada N[27]提出的方法确定。周伦伦[25]根据图8得到了对于考虑滚动阻矩的圆形颗粒和F=0.820、F=0.780的颗粒在水平推力T的作用下平面上滚动一周所做的功，再令等效颗粒滚动一周所做的功相等，即Wa=Wb=Wc，这样就可以得到形状系数F=0.820、F=0.780的clump颗粒的等效滚动摩擦系数ur,b和ur,c，根据颗粒面积等效原则，式（5）、式（6）可换算成关于 δ的表达式：

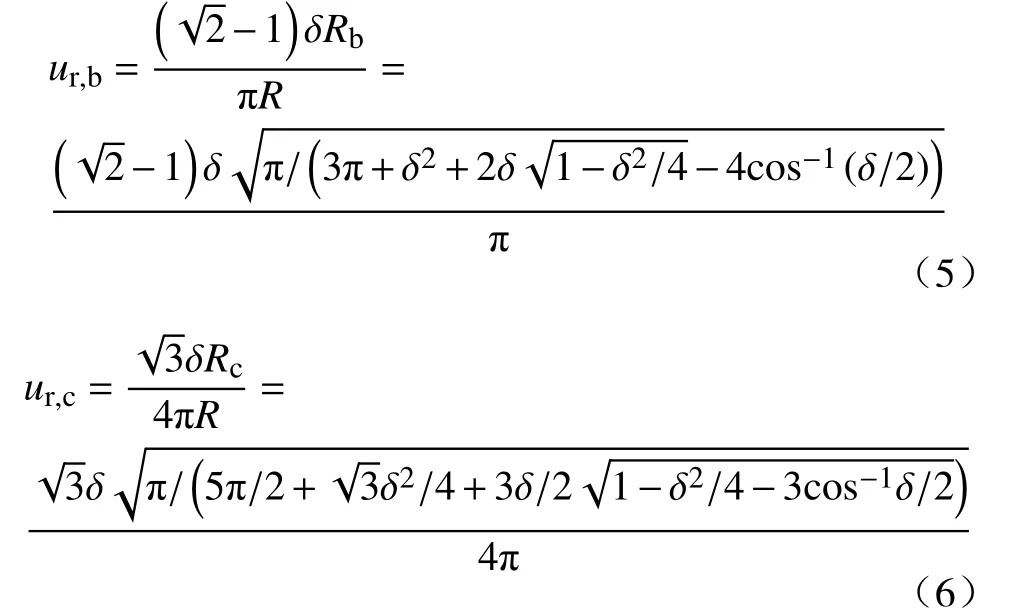
式中：δ-组元颗粒的间距。

δ增大，等效滚动摩擦系数增大，故ur,b＜ur,c，即F=0.820 受到的摩擦阻力要小于F=0.780的颗粒。在实际剪切过程中，异形颗粒之间有咬合作用，比在平面上滚动受到的阻力大，ur,b′＞ur,b，ur,c′＞ur,c，且ur,b'＜ur,c'，F=0.780的颗粒滚动摩擦系数比F=0.820颗粒增大的多，滚动时更困难。故形状系数F越小，颗粒间咬合摩擦作用更强烈，其咬合摩擦强度也越高，在宏观上反映为抗剪强度更高。

2 颗粒形状对粗粒土细观参数的影响

在法向应力作用下，粗粒土颗粒发生运动，致使试样重新排列，以适应法向应力变化引起的应力状态的改变。剪切过程中，粗粒土所表现出的宏观力学特征都是细观结构不断演化的结果。因此，对粗粒土试样剪切过程中细观组构参数的特点及其演化规律的分析，有助于进一步揭示颗粒形状与粗粒土剪切特性的对应关系。

2.1 颗粒形状对接触状态的影响

Oda[28]研究了平均接触数与抗剪强度之间的关系，研究表明，对于同一形状试样，抗剪强度在宏观上取决于初始密度和围压，在细观上取决于粒间的平均接触数。平均接触数越大，颗粒间的接触越充分，颗粒骨架体系能承担更大的外力。而剪胀现象的本质是颗粒体系在外荷载作用下发生运动和重新排列的结果，这一系列变化直接影响平均接触数。

通过监测4种试样接触数的变化情况，得到剪切过程中不同形状颗粒试样的平均接触数Cn的演变规律（图9）。由图9可知：当F=1.000，0.820，0.780，0.722时，初始平均接触数分别为3.67，3.99，4.15，4.31。平均接触数整体呈现先小幅增大，再大幅减小，最后趋于稳定。荷载的施加使得试样发生挤密，接触数有一定增加，当剪切继续时，颗粒发生运动，试样在外荷载作用下发生重排列，试样体应变增大，发生剪胀，平均接触数逐渐减小。形状系数F的减小使得Cn的峰值及稳定后的值越大。

图9 剪切过程中平均接触数Cn的演变规律Fig.9 Evolution law of the average coordination number cn in the shear process

根据颗粒直剪试验所获得的内摩擦角，得到初始平均接触数与颗粒形状系数F、内摩擦角φ与颗粒形状系数F的对应关系（图10）。颗粒形状系数影响着试样的初始平均接触数，且试样的抗剪强度受颗粒形状及其初始平均接触数的影响。其规律为：在同一初始孔隙率条件下，颗粒形状系数F减小，试样的初始平均接触数增加，内摩擦角φ增大，即抗剪强度增大。表明在相同孔隙率条件下，异形颗粒试样能与更多颗粒互相接触，即颗粒间接触更加紧密，试样整体结构会更加稳定，在宏观尺度上表现为异形颗粒抗剪强度更高。

图10 C0-F，φ-F 关系Fig.10 Relationship between C0 -F and φ-F

与接触数一样，孔隙率用于反映粒间接触的密实程度。以剪切带作为分界线，将试样分为剪切带、剪切带上侧及剪切带下侧3个条带，图11为F=1.000时孔隙率增量的演化过程。可以看出，剪切带内孔隙率均明显增大，说明剪切带内发生大幅度剪胀，导致试样整体的剪胀；剪切带外发生轻微剪胀或剪缩，对试样整体剪胀影响较小。

由图11可知，试样的大幅度剪胀发生在剪切带内，是影响整个试样剪胀幅度的关键。因此，对形状系数不同的另外3组试样剪切带内孔隙率增量的演化过程进行了统计，结果如图12所示。几种颗粒的孔隙率演化均符合随着剪切位移逐渐增大的规律，且颗粒形状系数越小，孔隙率增量越大。在相同法向应力作用下，纯圆颗粒的剪胀率最小，形状系数F越小，剪胀幅度越大。

图11 F=1.000时孔隙率的演化Fig.11 Evolution of porosity when F=1.000

图12 不同颗粒形状粗粒土剪切带内孔隙率的演化Fig.12 Evolution of porosity in the shear zone of coarse-grained soils with different particle shapes

2.2 颗粒形状对粗粒土力链变化的影响

当试样被施加外荷载时，相邻颗粒会相互接触，形成许多强度不同的力链，非均匀地分布在颗粒体系中。力链网络是宏观上用来表征土骨架体系上粒间接触力的形式，是颗粒体系受外荷载作用时受力响应机制的反应[29-30]。图13为4种颗粒试样在200 kPa法向力作用下同一时刻剪切带内的力链网络结构图。相较于初始时期，力链网络的强弱力链区分愈加明显，主要表现为强力链聚集并起骨架作用，且沿剪切盒对角线分布。

将F=1.000时的力链长度进行统计并得到其力链长度的概率分布（图14）。力链长度的分布概率随着力链的长度增大而减小，长度n=3的力链占比最高，n＞15的力链长度数目仅占3.39%。力链越长，引起其变化的因素就越多。对于过长的力链，在微小扰动下就会使长力链发生变化，甚至断裂成稳定的较短力链。统计4种试样的力链长度各自所占百分比并绘于图15，可见整体上表现出在力链长度0～5 范围内所占百分比最高。随着形状系数F的减小，力链长度在0～5所占百分比呈增大趋势。

图13 剪切过程中的力链网络Fig.13 Force chain network in the shear process

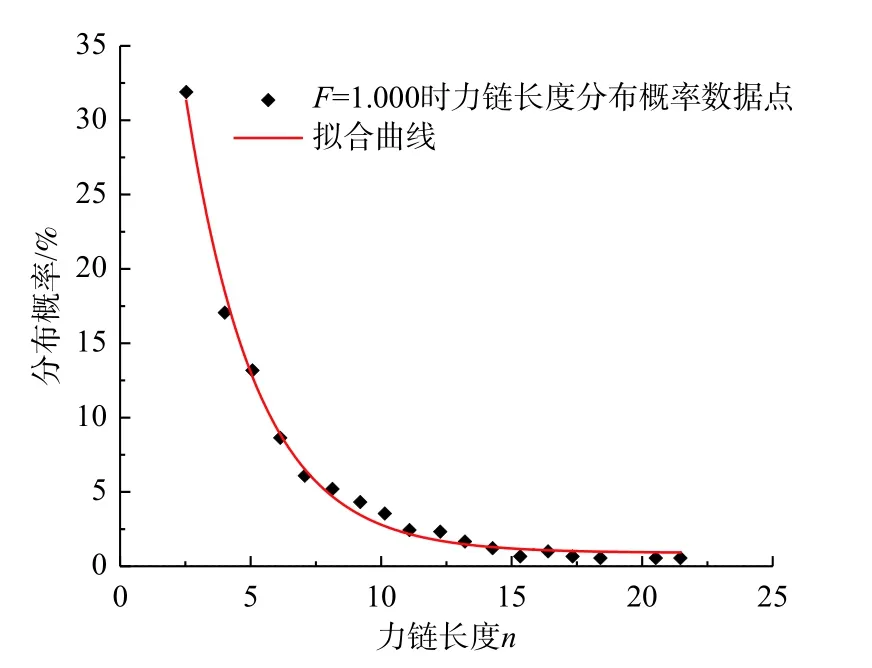
图14 力链长度分布概率Fig.14 Probability of the force chain length distribution

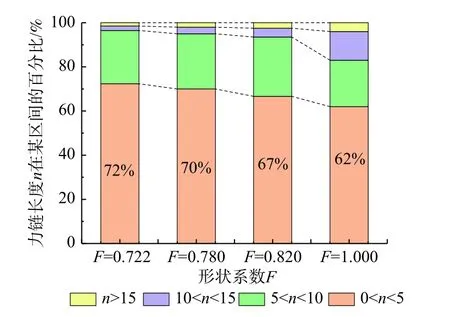
图15 不同形状系数试样的力链长度分布Fig.15 Force chain length distribution ofspecimens with different shape coefficients

为了进一步定量分析剪切过程中不同颗粒形状粗粒土粒间作用力的变化规律，本文研究中以200 kPa作为强弱力链的分界值，大于200 kPa的为强力链，小于200 kPa的为弱力链。利用Image Pro Plus 图像处理分析软件，分别统计了4种颗粒形状粗粒土剪切过程中，不同时刻剪切带内土体中不同力链的面积。用强力链的面积占被测区力链总面积的百分比，作为强力链的百分含量（图16）。

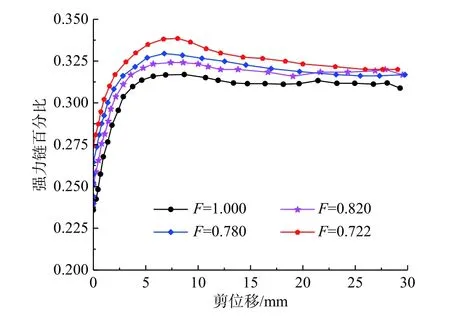
图16 不同颗粒形状试样剪切过程中剪切带内强力链含量百分比Fig.16 Evolution of the strength chain content percentage in the shear process of specimens with different particle shapes

图16中4种形状的粗粒土试样剪切带内强力链含量百分比所表现出的趋势较为一致。在剪切位移为零时，由于正应力的施加，颗粒间会发生挤密，产生一部分强力链；当剪切进行时，随着剪切位移的增加，剪切带内强力链逐渐汇集，且在剪切峰值时强力链的含量达到最大；越过峰值后，剪切带开始发生破坏，强力链也随之减少并逐渐趋于稳定。另外，峰值时，4种颗粒强力链占比在30%～35%之间，且随着形状系数F的减小，剪切带内强力链含量百分比呈增大趋势。

颗粒个体是互相离散的，颗粒体系的宏观变形和强度特性等主要取决于颗粒个体的空间排列及相互作用力。剪切过程中粗粒土颗粒间相互作用力的大小与土体宏观剪切应力的大小具有一定的对应关系：剪切过程中土体颗粒间的相互作用力越大，土体的宏观剪切应力也越大。

3 结论

（1）通过对剪切时颗粒剪切特性的分析，可知试样的应变主要表现在颗粒运动剧烈、剪胀幅度较大的剪切带内，剪切带外发生轻微剪胀或剪缩，对试样整体剪胀影响较小，说明剪切带的变化是影响整个试样变形的关键。

（2）剪切过程中，试样在外荷载作用下颗粒发生运动，试样剪切带厚度、平均接触数、孔隙率等宏细观参量发生变化，这些宏细观参量的变化也反映了剪切带内的剪胀现象。通过对试样的接触力系的分析：颗粒形状的不规则，导致剪切带内强力链的数目随着形状系数的减小而增加；另外，随着形状系数的减小，力链长度在0～5 范围内所占百分比呈增大趋势。

（3）异形颗粒间的咬合自锁作用大于纯圆颗粒，剪胀幅度随形状系数的减小而增大，对应的试样的抗剪强度随形状系数的减小而增大。