滑源区粒序分布及颗粒粒径对碎屑流冲击作用的影响研究

张志东，樊晓一,2，姜元俊

（1.西南科技大学土木工程与建筑学院，四川 绵阳 621010；2.工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621010；3.中国科学院成都山地灾害与环境研究所，四川 成都 610041）

滑坡碎屑流是我国山区常见的地质灾害，具有突发性高、破坏性强的特点，严重威胁着山区的交通工程、建筑安全，其致灾机制和防治措施是山区工程建及设防灾减灾需要解决的关键问题。滑坡碎屑流的颗粒粒序分布和粒径是影响其致灾速度、拦挡堆积和冲击力分布的重要因素。滑源区岩体性质的差异及结构分布控制了滑坡碎屑流运动过程中的粒径大小和运动分布。一般而言，强度高的坚硬岩体在运动过程中，破碎程度较低，易形成大粒径块体；强度低的软岩体在运动过程中颗粒破碎程度高，易形成小粒径块体；而介于之间的较硬岩体易形成中等粒径的块体。此外，处于不同地层的岩体，其内部结构的差异同样会造成破碎程度的差异。因此，明确滑源区粒序分布及颗粒粒径对滑坡碎屑流冲击作用的影响，对滑坡碎屑流的预防与治理及建筑结构的设计与规划具有重要的科学意义。

由于碎屑流内部不同粒径大小的颗粒其物理力学性质存在差异，粗大颗粒的碰撞分离有利于块体之间的能量传递[1-3]，对滑体冲击作用影响显著；而高速流动的细粒组分，在上部滑体物质的压力下有利于滑动面颗粒液化效应，并使得碎屑流速度进一步提升[4]。此外，大、小粒径颗粒的含量、粒径差还会影响颗粒的分选程度及堆积形态[5-7]；碎屑流的粒序排布可分为正粒序、反粒序和混杂粒序3种，部分研究结果表明，不同的初始粒序排布会通过不同颗粒分选模式造成不同的冲击效应，并塑造出不同的反粒序堆积形态[8]。因此滑坡碎屑流岩土体粒径大小及粒序分布制约着滑体的运动特征，影响了滑体的冲击作用，决定了碎屑流的致灾程度。不同粒径大小及粒序分布的岩土体，其运动过程中的速度-时程分布与演化、堆积形态及长度、深度分布特征和冲击力等因素关系到碎屑流致灾机制的研究。

虽然运用能量传递理论[1-3]、振动筛分假说[9-10]、颗粒分选效应[11-13]的理论模型能较为合理地解释碎屑流运动特征及冲击作用，物理模型试验研究[14-16]及数值模拟研究[17-20]也基本还原、验证了实际碎屑流的运动及冲击参数，但现有研究对不同岩性结构和组合控制的颗粒粒径及滑源区初始粒序分布对滑体运动和冲击作用影响的探讨较少。本文在物理模型试验[14]的基础上。运用离散元软件PFC3D建立颗粒、滑槽与挡墙的数值模型，在取得物理模型验证的基础上，探究滑源区粒序分布及颗粒粒径对碎屑流冲击作用的影响，为滑坡碎屑流预防与治理、建筑结构设计与规划提供理论参考。

1 三维离散元模型

1.1 模型建立

如图1所示，碎屑流底板长2.7 m，滑槽宽0.3 m，高0.35 m，挡墙与滑槽等高，滑源区设置料槽，长0.44 m，高0.2 m，宽0.3 m，料槽前设置激发门，距挡墙2.19 m，滑槽倾角30°。

图1 滑槽模型示意图（单位：mm）Fig.1 Sketch of the flume model (mm)

本文选用整体质量相等的Large颗粒、Mid颗粒与Small颗粒，分别模拟粒径为40 mm、20 mm 与10 mm的大、中、小碎屑流颗粒。结合实际滑坡中滑源区不同位置的不同岩性[21-23]（图2）及同一岩性地层的不同内部构造（如整体状结构、块状结构、碎裂状结构、散体状结构等），考虑不同地层岩土体破碎时块体颗粒粒径大小（硬岩破碎时易形成大粒径颗粒、软岩易形成小粒径颗粒），设置7组碎屑流初始堆积体的粒序分布（表1），设置不同粒序分布的初始堆积体（图3）。

图2 滑源区不同位置处的岩性Fig.2 Different lithologies in the slip source area

表1 数值模拟中岩土样粒径分布Table1 Gradation composition of the samples in the numerical simulation

图3 各工况初始堆积体粒序分布图Fig.3 Grain order distribution of the primary deposits under different working conditions

1.2 参数标定

本文采用PFC3D软件中的Hertz-Mindlin模型对滑槽实验进行数值模拟，在Hertz-Mindlin模型中材料的基本本征参数主要包括：剪切模量、泊松比、摩擦系数、密度和法向、切向黏性阻尼比。

离散元模拟中，泊松比、剪切模量和密度（真实密度）为材料的本征参数，表示各种材料的自身属性，与外界条件无关，改变滑体粒序和粒径不会影响材料属性，可直接用于数值模拟，故基于模型试验及计算结果，确定其参数（表2）。摩擦系数是指两表面间的摩擦力和作用在其一表面上的垂直力之比值，和表面粗糙度有关，由于实验中真实颗粒的不规则形状与数值模拟中球形外形存在差异，使得通过实验测得的摩擦系数不能直接用于数值模拟中，故需通过多次调试数值模拟中的摩擦系数，以使模拟结果与模型试验结果吻合，黏性阻尼相当于在颗粒法向上添加的弹簧，切向上添加阻尼器，其值主要反映颗粒碰撞、摩擦时引起的能量耗散。根据试验计算得到的法向黏性阻尼为0.16，切向黏性阻尼为0.07。由于模拟颗粒为规则球形，导致与实际颗粒相比碰撞较少，能量损耗不足，故通过适当增大黏性阻尼的方式增大颗粒流内部的耗能，为此通过多次调试并对比模型试验结果确定法向阻尼为0.60，切向阻尼为0.07。

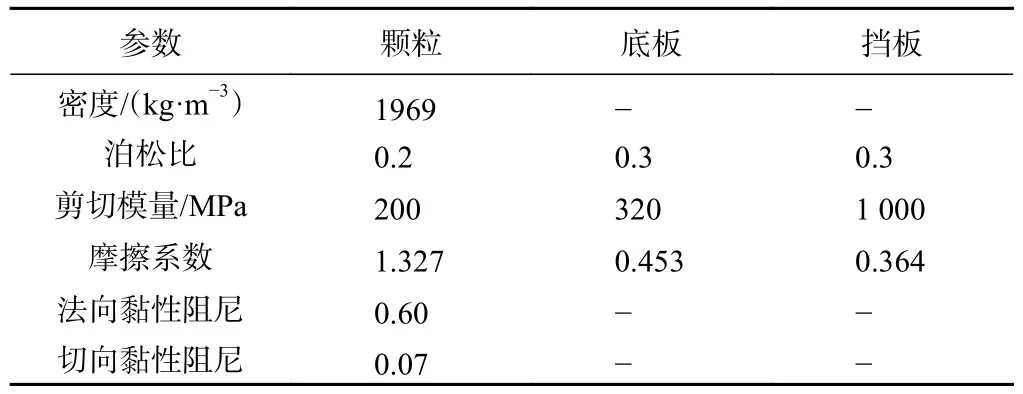
表2 模拟参数Table2 Parameters used in the model

2 模型验证

鉴于模型试验中的颗粒级配较为连续，运用筛分的方式无法单独分离出粒径单一的Large、Mid、Small颗粒，故在模型试验中以不同粒径范围内的颗粒分别表示Large、Mid、Small颗粒（以1～10 mm的颗粒为Small颗粒，10～20 mm的颗粒为Mid颗粒、20～40 mm颗粒为Large颗粒）。表3及图4记录了模型试验中滑体的3组级配分布。在相同颗粒级配、滑槽坡度条件下，通过还原模型试验全过程，对模型试验与数值模拟的运动过程、冲击力变化规律进行比对分析，验证数值模拟所取参数的可靠性，为下一步运用数值模拟探究滑源区粒序分布对碎屑流不同粒径颗粒冲击作用机理研究提供依据。

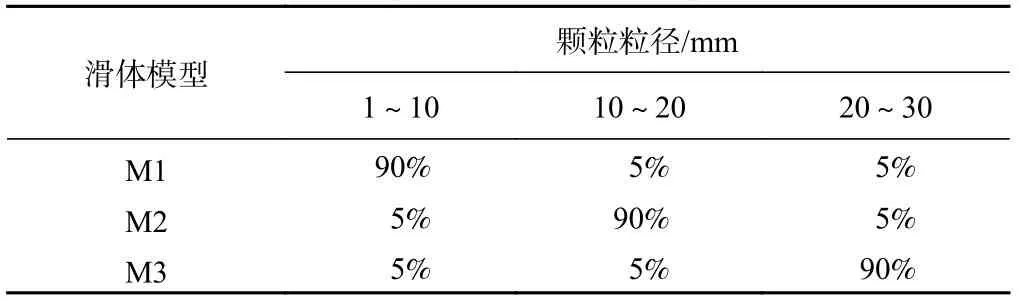
表3 模型试验岩土样级配组成Table3 Gradation compositions of the samples in the model test

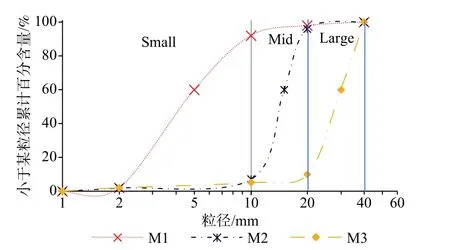
图4 滑体模型试验级配曲线Fig.4 Curve of gradaton of the samples

以滑体模型M2（颗粒见图5）为例，图6为坡度为30°、35°、45°时数值模拟与模型试验的颗粒堆积形态的对比，可见模拟结果与实验结果吻合较好。数值模拟与模型试验的冲击力曲线（图7）同样较为接近（最大误差不超过8%）进一步证实了参数的可靠性。

3 颗粒粒径及滑源区粒序分布对碎屑流运动特征的影响

3.1 对碎屑流运动速度的影响

3.1.1 颗粒粒径对碎屑流平均速度的影响

图5 M2级配颗粒材料Fig.5 Grain material of the M2 grade

图6 不同坡度模型试验与数值模拟的颗粒堆积形态对比Fig.6 Comparison of the deposition forms between the numerical simulation and model test under different slopes

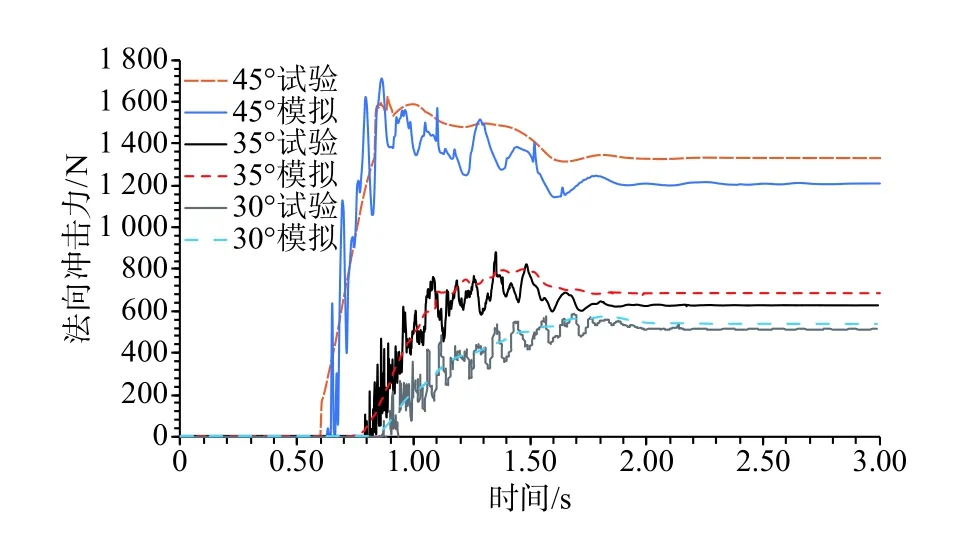
图7 不同坡度下数值模拟与模型试验冲击力对比Fig.7 Comparison of impact force between the numerical simulation and model test under different slopes

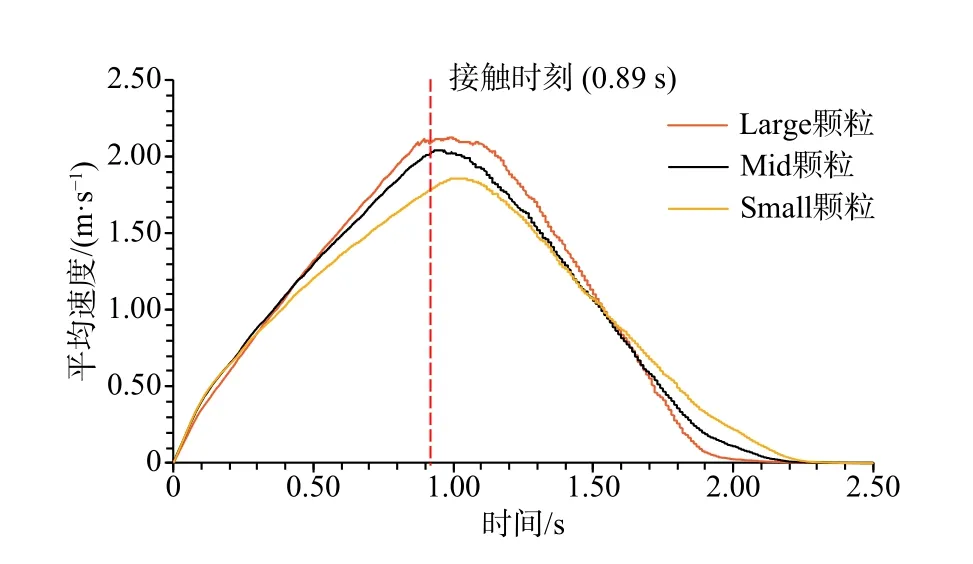
图8 MIX工况下不同粒径颗粒的平均速度时程曲线Fig.8 Time-history curve of the average speed of particles with different particle sizes under the MIX conditions

在初始时刻，MIX工况条件下3种颗粒在空间位置上的分布均服从高斯函数，这导致3种颗粒整体的重心位置相同，从而使得颗粒的不同初始粒序分布对速度造成的影响可以忽略不计，故可得到颗粒粒径这一单一因素对平均速度的影响。如图8所示，3种颗粒平均速度的变化规律是一致的，均为先增大后减小，这反映出3种颗粒相似的运动过程，即颗粒先在重力的作用下做加速运动，随着颗粒在滑槽上充分展开（图9a），平均速度逐渐达到最大，而当颗粒在受到挡墙拦挡作用后速度逐渐减小并趋向0。然而，在碎屑流前缘与挡板接触的时刻，颗粒的平均速度并未达到最大值（平均速度最大时碎屑流的运动状态见图9b），这是因为虽然碎屑流前缘已经受到挡墙的拦挡作用，但碎屑流的中后缘仍然在做加速运动，所以碎屑流的整体速度仍在增大，即平均速度的峰值时刻要略微滞后于颗粒与挡墙发生接触的时刻。图8中，MIX工况下3种颗粒的平均速度峰值及达到峰值的时刻对比表明：大粒径颗粒的平均速度和峰值速度最大，到达峰值时刻的历时最短，且随着峰值速度的增大，达到峰值所需的时间减少。

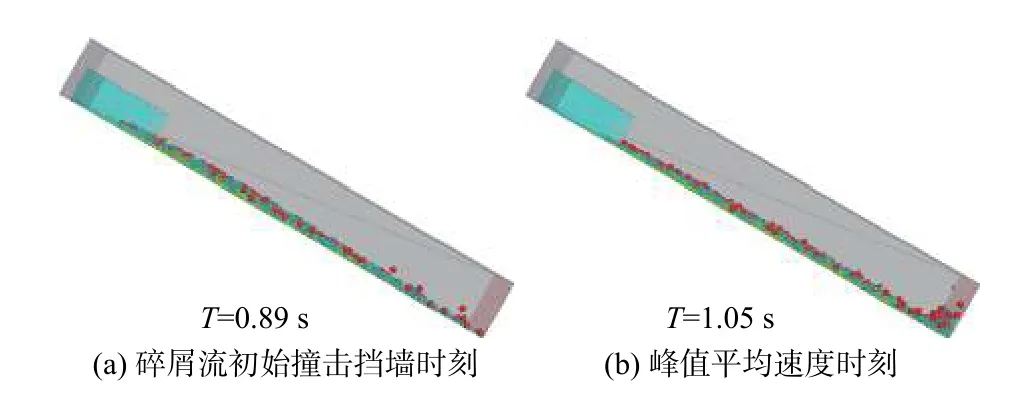
图9 MIX工况下不同时刻运动对比Fig.9 Movement comparison at different moments under the MIX conditions

3.1.2 初始粒序对碎屑流平均速度的影响

表4、表5记录了3种不同颗粒在7种工况条件下颗粒平均速度峰值及达到峰值所需的时间。结合图10，对颗粒平均速度作对比可以发现：颗粒初始空间分布会显著影响不同颗粒的平均速度峰值及其对应时间，即某种颗粒初始分布位置越靠近堆积体的表层，其平均速度的峰值越大，达到峰值所需的时间越短。反之，某种颗粒的初始分布位置越靠近底层，平均速度的峰值越小，达到峰值所需的时间越长。其原因在于：（1）不同分布方式造成的重心位置不同（越靠近初始堆积体表层，重心位置越高，反之越低）；（2）位于表层的颗粒与内部颗粒接触面积较小，使得其受到的摩擦力较小，而位于底层的颗粒同时要与上部颗粒和下部滑道接触，导致其受到的阻力较大。

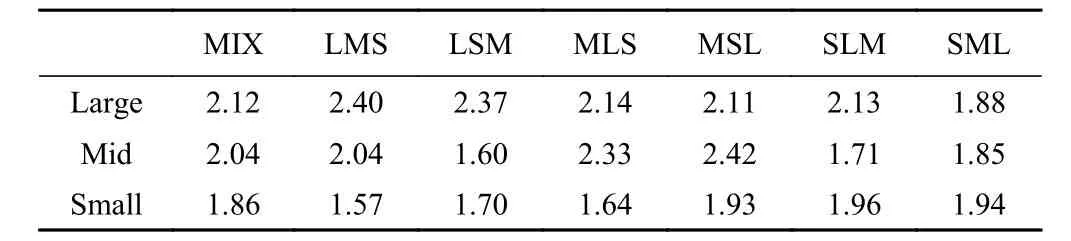
表4 不同工况下的平均速度峰值Table4 Average maximum speed under different working conditions /（m·s-1）

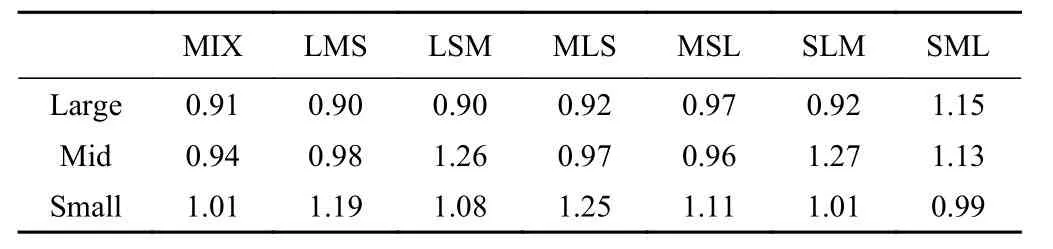
表5 不同工况下平均速度峰值时刻Table5 Time of the average maximum speed under different working conditions /s

图10 3种颗粒在不同工况下的平均速度时程曲线Fig.10 Curve of the average speed vs time of three kinds of particles under different working conditions

3.1.3 初始粒序及颗粒粒径对碎屑流平均速度耦合影响

茄子幼苗度过缓苗期后会逐渐步入到快速生长期，这个时期温室大棚白天温度控制在30℃以下，温度太高会造成花器发育不良，影响茄子结实。夜间温度控制在15℃以内。当茄子进入开花坐果期后，可以选择晴朗天气，在早晨使用30 ppm的2，4-D或者防落素对番茄花和植株进行处理，增强植株开花坐果能力，促进果实快速膨大，提高茄子产量。

由前述可知，3种不同颗粒的平均速度受到颗粒粒径和滑源区粒序分布的共同作用。但两种因素的强弱关系仍需进一步讨论。如表4所示，在非混合情况的6组工况条件下，LMS、LSM、MLS工况中3种颗粒平均速度峰值与其相应的初始空间分布位置存在一一对应的关系。以MLS工况为例，其初始粒序为：Mid颗粒在最上层，Small颗粒位于最下层，Large颗粒处在二者中间，恰好与速度峰值的大小存在对应关系（VMid＞VLarge＞VSmall）；而MSL、SLM、SML则不完全对应，但仍然部分对应（MSL工况下Mid颗粒的平均速度峰值最大、SML工况下Small颗粒的平均速度峰值最大，SLM工况下Small颗粒的速度峰值仍然比Mid颗粒大）。而颗粒大小与最大平均速度的对应关系则较不明显（除去工况MIX）。

速度峰值的出现时刻如表5所示，LMS、LSM、MLS 3组工况中3种颗粒平均速度峰值的出现时刻与其相应的初始空间分布位置也存在一一对应的关系，以LSM工况为例，其初始粒序为：Large颗粒在最上层，Mid颗粒位于最下层，Small颗粒处在二者中间，恰好与速度峰值出现时刻存在对应关系（TMid＞TSmall＞TLarge）。而MSL、SLM、SML 则不完全对应但仍部分对应。

综上，碎屑流在运动过程中，其速度峰值及峰值出现时间既受到颗粒粒径的控制，又受滑源区粒径空间分布的影响，且粒序分布起主要作用，颗粒粒径起次要作用。故在碎屑流速度分析及相关研究方面，应重点考虑粒序分布造成的影响。

3.2 对碎屑流堆积形态的影响

碎屑流的最终堆积形态可以从侧面反映出碎屑流在冲击挡墙过程中冲击作用的相关特性以及挡墙在承受冲击作用时的动力响应机制。表6 记录了碎屑流冲击挡墙后的侧面堆积形态。为避免二维视图造成的颗粒重叠，对颗粒做半透明化处理（透明度70%），并分别对3种颗粒进行单独监测，从而更直观地显示3种颗粒在堆积体中的空间分布。从碎屑流的整体堆积形态看，LMS、LSM工况下碎屑流堆积体的堆积长度较长，堆积高度较低，堆积体表面较平坦。相反，SLM、SML工况条件下，堆积体的堆积长度较短，堆积高度较高，堆积表面呈圆弧状。而MLS、MSL工况下堆积长度和高度与SLM、SML工况相似，但其堆积表面轮廓呈不规则状，即存在一个“偏转点”（图11），使得堆积体表面轮廓发生较大变化。而对某种单一颗粒在不同工况条件下的堆积形态进行对比观察发现：碎屑流启动前，若某种颗粒越靠近初始堆积体表面，则冲击作用结束后其堆积形态越接近三角形（图12a），平均堆积长度越短（表7）。相反，若某种颗粒越靠近初始堆积体底面，冲击完成后，其堆积形态越接近长条形（图12b），表面轮廓越接近拱形，且平均堆积长度越长。这表明，初始时刻不同粒径颗粒的分布位置和排布方式会造成不同的沿长度、高度方向的堆积粒序排布，且区别于长度方向上堆积体粒序分布特征，任何工况条件下，不同颗粒在高度方向的分布皆严格遵循“上大下小”的反粒序分布规律（表8）。这表明沿高度（厚度）方向上的分选效应主要受粒径大小的影响，而初始时刻堆积体的粒序分布对其影响较小。

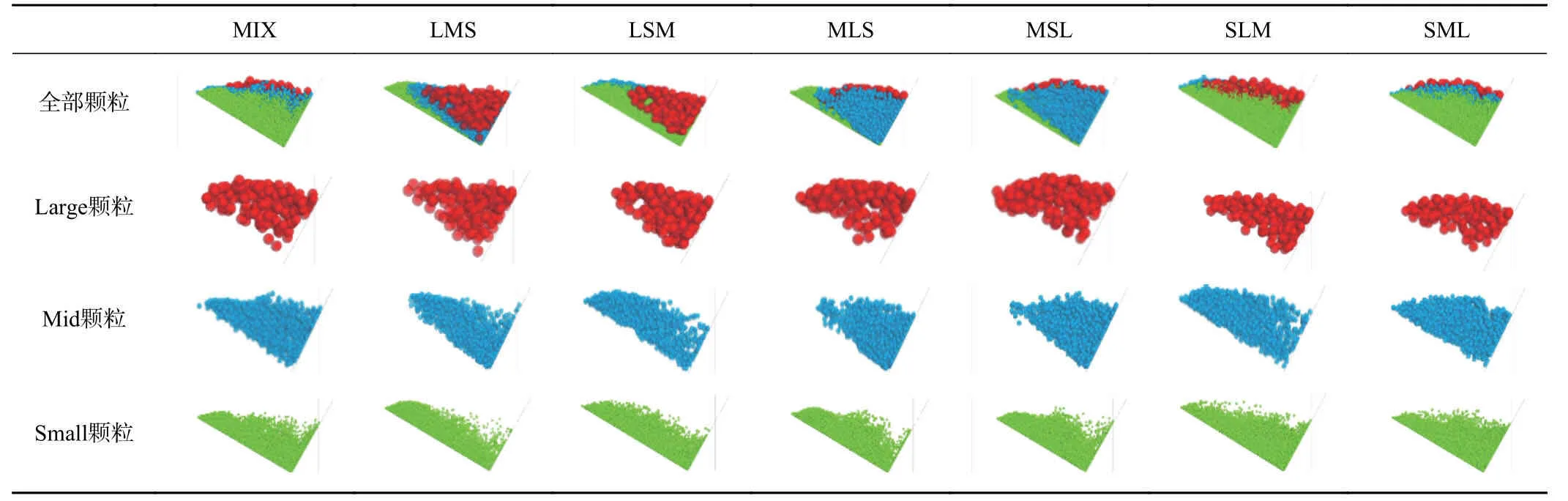
表6 碎屑流冲击挡墙后的侧面堆积形态（侧视图）Table6 Side deposit shape after the impact on the parapet by the fluidized landslide-debris flow (side view)

3.3 对挡墙所受冲击力的影响

滑体冲击挡墙的过程可划分为动态冲击阶段和准静态堆积阶段[8]（图13、图14）。

动态冲击过程中，前缘滑体与挡墙直接碰撞接触并堆积于挡墙底部，后续滑体越过前缘堆积物继续冲击挡墙，堆积体高度不断增加。准静态堆积阶段，堆积体高度基本保持稳定，挡墙所受冲击力主要为后续滑体颗粒重力分量的累积以及后续颗粒冲击能量的碰撞传递。两种阶段冲击力的作用方式、挡墙的动力响应均有较大差异，故应分开讨论。此外，需要注意的是，图13中数值模拟的冲击力曲线与图7中倾角30°的物理模型试验冲击力曲线有较大差异，数值模拟的冲击力明显偏小，这是因为数值模拟中的颗粒为3种单一粒径颗粒的有序排列。其相同粒径颗粒较多导致颗粒间的空隙较大，滑体松散程度较高。相反，模型试验采用连续的粒径级配曲线，颗粒间的空隙较少，滑体较密实。故而在同等体积下，模型试验中较密实的滑体对挡墙造成了较大的冲击力。

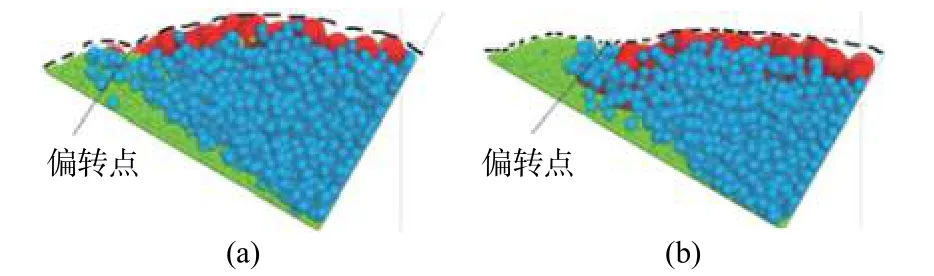
图11 工况MLS（a）和MSL（b）下滑体堆积形态Fig.11 Deposit shape of the sample under the (a) MLS and(b) MSL working conditions

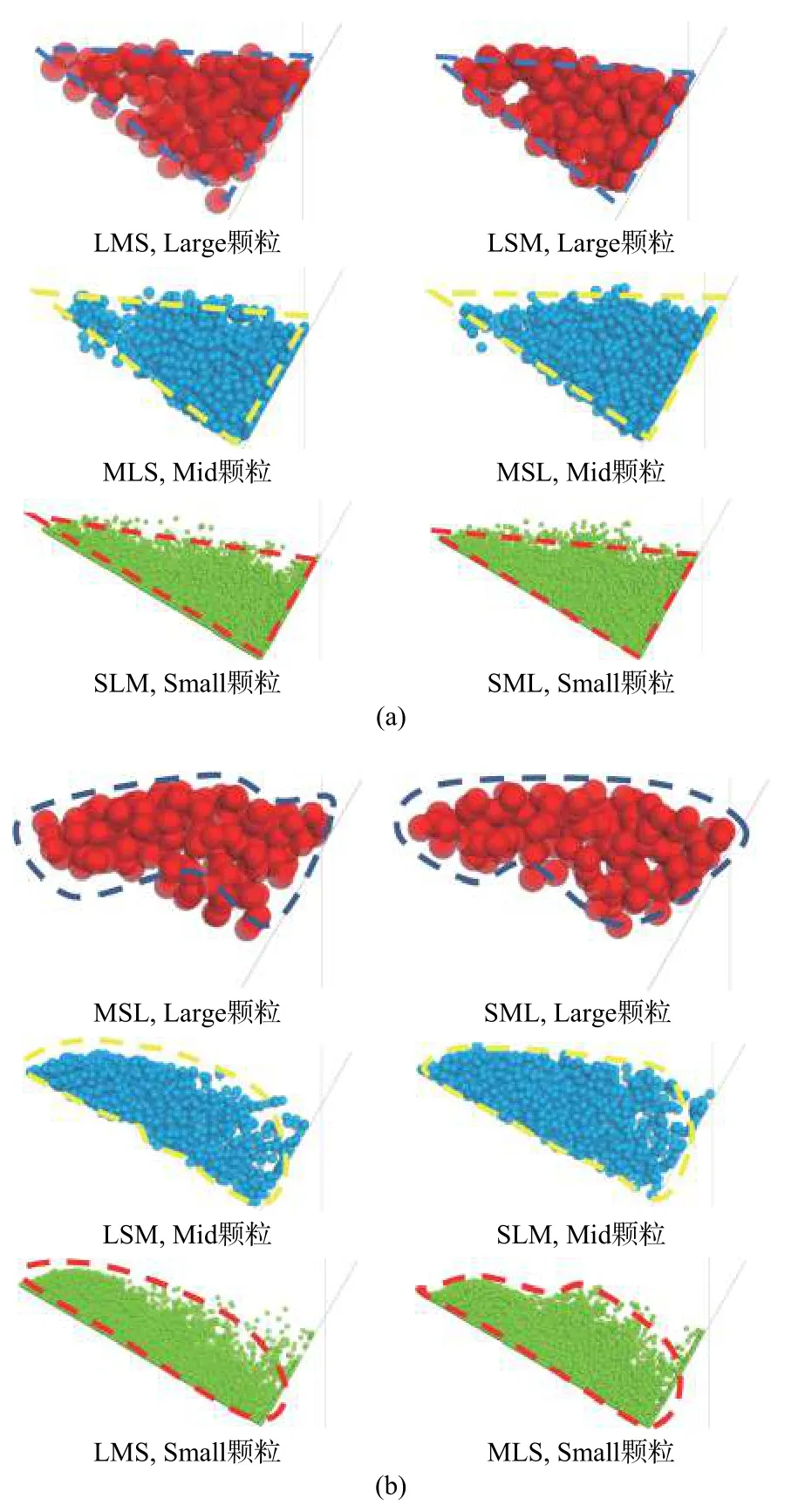
图12 单颗粒靠近初始堆积体表面时（a）和底面时（b）不同工况下3组不同颗粒单粒的堆积形态Fig.12 Deposit shape of the three groups of different particles under different working conditions when the single particles close to (a) the surface and (b) the bottom of the initial accumulation body

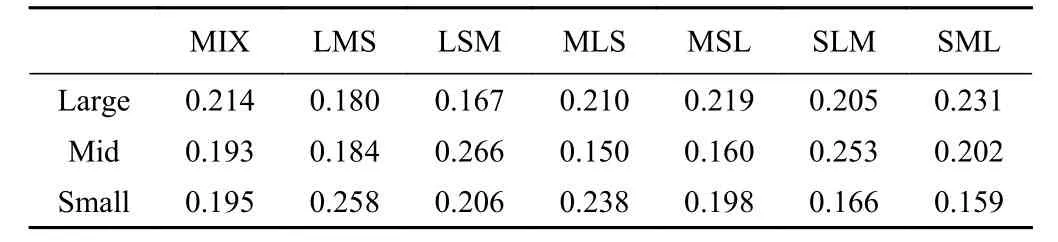
表7 3种颗粒的平均堆积长度Table7 Average deposit length of three kinds of particles/m

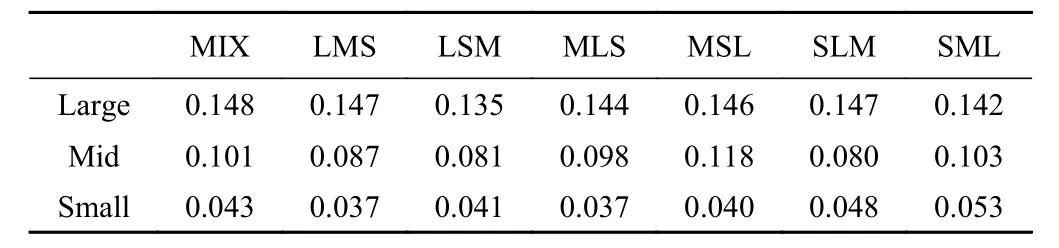
表8 3种颗粒的平均堆积高度Table8 Average deposit height of three kind of particles /m

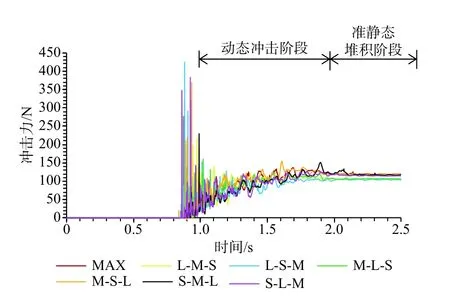
图13 冲击挡墙阶段各工况冲击力时程曲线Fig.13 Time-history curves of the impact force under various working conditions during the impact retaining wall

3.3.1 动态冲击阶段

在动态冲击阶段，衡量冲击力最重要的指标是冲击力峰值，不同工况条件下各种颗粒的冲击力峰值及峰值对应的时刻如表9、表10所示（图15为3种颗粒在不同工况条件下对挡墙的冲击力作用）。对比每组工况内3种颗粒整体冲击力峰值可知，在颗粒质量相同的条件下（表1），粒径较大的Large颗粒整体对挡墙的冲击力峰值明显高于其他两种颗粒。而对于Mid颗粒和Small颗粒，二者整体冲击力峰值的大小关系则决于二者初始空间位置的相对分布（初始位置更靠近堆积体表面的颗粒，其整体冲击力峰值更大）。这反映了颗粒粒径和初始堆积体粒序对碎屑流冲击力的共同作用，且颗粒粒径的影响更大，因为通过对Large颗粒和所有颗粒的整体峰值冲击力及峰值冲击力的出现时刻作对比可以发现，Large颗粒与全部颗粒的整体峰值冲击力非常接近，且出现时刻基本一致，这体现了Large颗粒的整体峰值冲击力对碎屑流整体峰值冲击力的重要贡献。此外，在不同工况条件之间，Large颗粒和Mid颗粒的整体冲击力峰值未显示出明显的规律（表9），表明粒径较大的颗粒在不同初始粒序分布条件下，其整体冲击力峰值具有一定随机性。而Small颗粒则仍然具备一定规律，即初始分布位置越接近堆积体表面，其整体冲击力峰值越大。

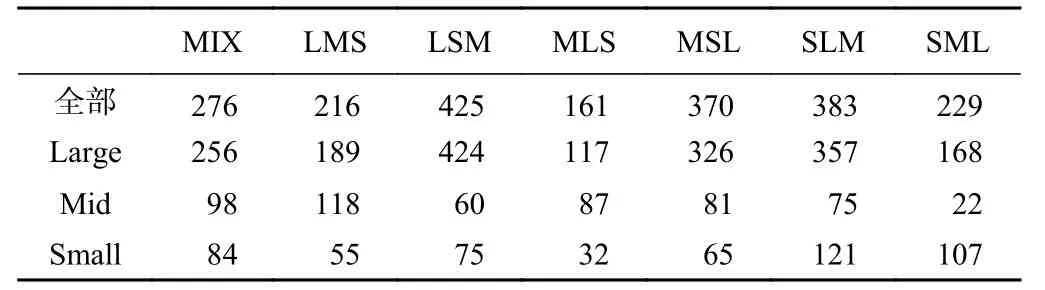
表9 各颗粒的整体峰值冲击力Table9 The maximum impact force of each kind of particles /N

表10 各颗粒整体峰值冲击力作用时刻Table10 Time of the maximum impact force of each kind of particles /s

为进一步量化分析颗粒粒径对碎屑流峰值冲击力的影响。对碎屑流峰值冲击力的贡献率进行统计（即碎屑流最大冲击力时刻，各颗粒整体冲击力占总冲击力的百分比）。表11 记录了各工况条件下不同粒径的粒组对碎屑流整体峰值冲击力的贡献率。Large颗粒对碎屑流整体冲击力峰值的贡献率占据明显优势（均在50%以上，且有3组超过90%），这表明粗大颗粒的瞬时撞击是造成峰值冲击力的主要原因，而初始粒序对碎屑流峰值冲击力的影响较小，且只能在中小颗粒中起作用（Mid和Small颗粒中越靠近初始堆积体表面者，其对峰值冲击力的贡献率越高）。

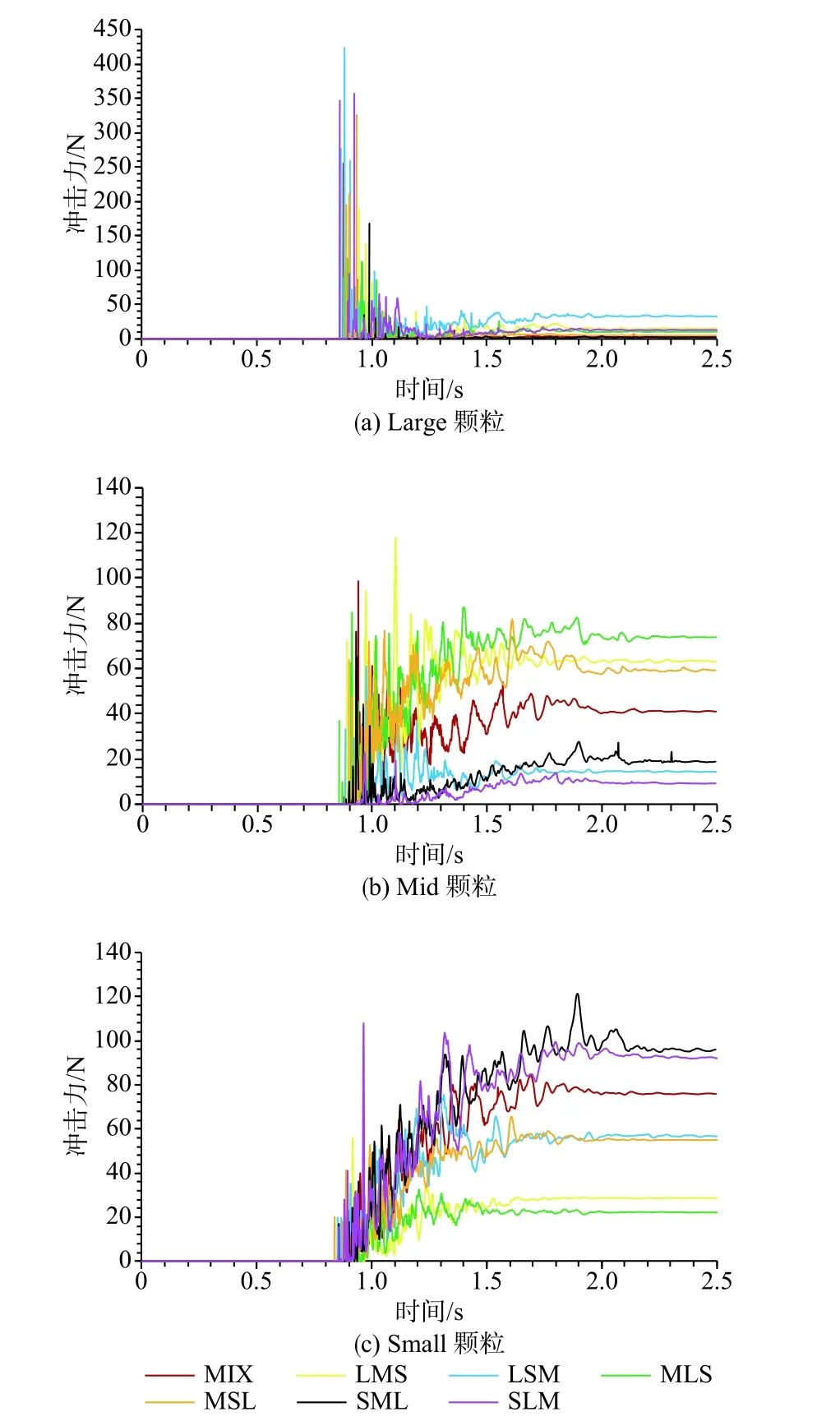
图15 3种颗粒在不同工况下的整体冲击力时程曲线Fig.15 Time-history curves of the impact force of three kinds of particles under different working conditions

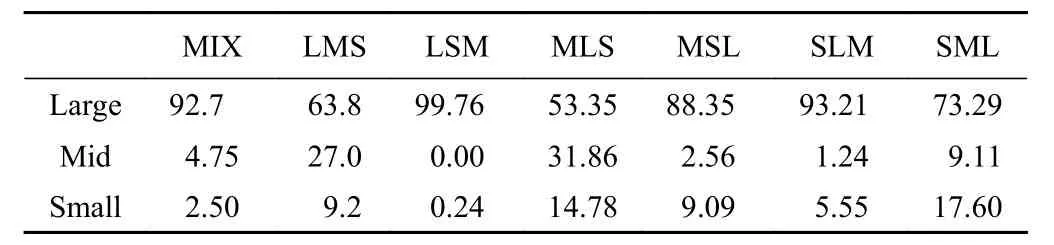
表11 3种颗粒峰值冲击力在滑体峰值冲击力中的占比Table11 The maximum impact force of three kinds of particles as a percentage of the maximum impact force of the sliding body /%

3.3.2 准静态堆积阶段

在准静态堆积阶段，碎屑流颗粒对挡墙的冲击力远小于峰值冲击力，并基本保持稳定，只在一定范围内作微小的上下波动。表12 记录了碎屑流完全停积后（2.5 s）挡墙的受力情况，能较好反映准静态堆积阶段挡墙的受力情况。

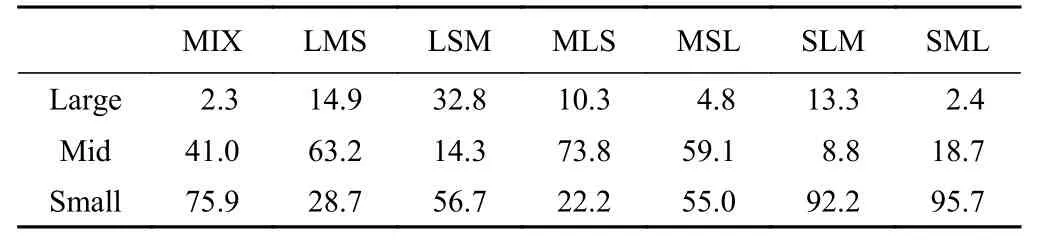
表12 3种颗粒准静态冲击力Table12 Quasi-static impact force of three kinds of particles /N

如表12和图15所示，不同工况之间同种颗粒的准静态冲击力呈现明显的规律性，即某种颗粒越靠近初始堆积体表面，其整体准静态冲击力越大。而在单一工况条件下，3种颗粒间的准静态冲击力规律性不够明显，但总体呈现Small颗粒的整体静态冲击力较大，Large颗粒的整体静态冲击力较小的规律，并且从MIX工况下静态冲击力的统计结果表明，颗粒粒径越小，其整体的准静态冲击力越大。

综上，在动态冲击阶段，控制峰值冲击力的主要因素为颗粒粒径，次要因素为初始堆积体粒序。相反，在准静态冲击阶段，控制某种粒径颗粒冲击力的主要因素为初始堆积体粒序，次要因素为颗粒的粒径。

4 讨论

通过对7种工况条件下的滑体模型进行数值模拟试验，探讨滑源区粒序分布及颗粒粒径对滑坡碎屑流运动堆积特征及冲击作用的影响机制。

对于滑源区粒序分布为混合粒序（MIX工况）的初始滑体，碎屑流在运动过程中，大粒径颗粒整体在消散压力的作用下向滑体表层运动，细小碎屑颗粒在运动筛分过程中向底板运移，即颗粒分选效应。颗粒的分选效应使得顶部的大颗粒基本不与滑槽底面接触，而只在其底部与下部颗粒部分接触，导致大颗粒受到的摩擦阻力较小，运动速度较大，而较大的运动速度又结合较大的单位质量使得单个大颗粒获得极大的动能，进而在与挡墙碰撞时转化为碎屑流的峰值冲击力。相反，由于底部的细小颗粒既要与上部的较大颗粒接触，又与底面的滑槽接触，导致其受到的摩擦阻力较大，动能损耗较大，使得其对峰值冲击力的贡献较小。

对于滑源区粒序分布为规则粒序的初始滑体（内部颗粒存在明显分层现象的滑体）。不同的初始粒序起到了与颗粒分选相似的作用机制，即在颗粒运动初期，位于表层的颗粒由于受到的阻力较小，导致其达到的平均速度峰值较大；而位于底层的颗粒由于受到的阻力较大，导致其达到的平均速度峰值较小，这表明滑源区上部的细小颗粒的平均速度峰值可能大于下部粗大颗粒（SML工况、SLM工况），但由于颗粒分选效应仍然存在，使大颗粒仍然有向碎屑流表层运动、小颗粒仍然有向碎屑流底层运动的趋势，即颗粒分选效应仍然会作用于滑体，并减弱滑源区粒序分布造成的“表层加速、底层减速”的效果，从而减小了大小颗粒之间的峰值速度差。因而导致了在不同滑源区粒序分布条件下，峰值冲击力仍由大粒径颗粒控制的现象，即在大小颗粒速度相差不大的情况下，颗粒粒径成为了峰值冲击力的主要控制条件。

由于滑源区初始粒序造成的速度差异，使得各种颗粒的堆积形态存在明显区别，即，处于滑源区上层的颗粒整体上由于平均速度较大，导致其在运动过程中处于碎屑流前端，并在冲击挡墙过程中受到后部其他颗粒的推挤、抬升，最终形成较为形状规则且长度较短的三角形。相反，处于滑源区下层的颗粒，由于平均速度较小，使得其在冲击挡墙过程中不断受到前缘颗粒的阻碍，使其速度进一步降低，动能减小，停积长度增加，最终形成表面存在一定弧度的拱形。而不同的堆积形态，又造成了不同的传力机制：三角形形状规则，长度较短，有利于冲击力的传递，导致位于滑源区表层的颗粒在准静态冲击阶段具有较大的冲击力。相反，拱形作为典型的承压结构，有利于冲击力的耗散，导致位于滑源区底层的颗粒在准静态冲击阶段具有较小的冲击力。

5 结论与建议

（1）碎屑流中各粒径颗粒的平均速度受颗粒粒径及滑源区初始粒序的共同影响，且初始粒序对各颗粒平均速度影响更大。在初始粒序为混合分布条件下，受颗粒分选效应影响，粒径越大的颗粒其峰值平均速度越大，而在非混合粒序条件下，由于初始粒序对颗粒分选效应的影响，导致颗粒越靠近初始堆积体表面，其峰值速度越大。

（2）碎屑流的最终堆积形态受初始堆积体粒序分布和粒径的共同影响。由于颗粒分选现象的存在，导致在厚度方向，粒径对堆积体堆积形状影响较大。而在长度方向，滑源区粒序分布通过控制碎屑流的速度大小，决定了堆积体的形状。

（3）碎屑流对挡墙的冲击可分为动态冲击和准静态堆积两部分，在动态冲击阶段，受颗粒分选效应的影响，颗粒粒径是峰值冲击力的主要控制因素，即粒径越大，峰值冲击力越大。在准静态堆积阶段，初始粒序起到了与颗粒分选相似的作用机制：促进了表层颗粒速度的增加而抑制了底层颗粒速度的增加，同时通过塑造堆积体形状，控制了准静态冲击力的大小。

（4）对于混合粒序的初始滑体，颗粒分选效应使得大粒径颗粒升至滑体表面，获得较大的速度和动能，最终转化为峰值冲击力；较小粒径颗粒沉至滑体底部，在内部剧烈摩擦作用下，获得较小速度和动能，使其对峰值冲击力的贡献较小。

（5）受限于试验材料和检测手段等客观因素，在模型验证方面未能通过模型试验完全还原数值模拟的相关内容，且未能将数值模拟所得的相关结论与同等模型试验的结论相印证。此外本次研究未能充分考虑滑动距离、更大颗粒粒径范围、实际地形条件等客观因素对颗粒分选机制的影响。

（6）进一步的工作已渐次开展，包括设计与数值模拟一致的模型试验、扩大滑体材料的粒径范围、在滑槽试验的基础上模拟实际地形条件下滑源区粒序分布及颗粒粒径对碎屑流冲击特性的影响等。