基于CEEMD 的冲击回波分析方法研究
2021-01-21朱先祥许军才倪福海
朱先祥 , 许军才 , 倪福海 , 丁 伟
(1.无损检测技术教育部重点实验室(南昌航空大学),南昌 330063;2.河海大学 力学与材料学院,南京 210098;3.安徽中盛建设工程试验检测有限公司,合肥 230051)
0 引言
冲击回波法是混凝土结构质量检测中一种常见无损检测方法。该方法是根据纵波在结构中的传播特性对结构质量进行检测,其原理如图1 所示[1-2]。利用钢锤敲击待测结构表面,冲击产生的振动波在结构内部传播过程中,当遇到一定尺度的缺陷或边界,因2 种材料的波阻抗不同而发生反射和透射现象,结构冲击表面上的质点就会产生振动响应,这种振动响应以加速度的信号形式被传感器采集到,再通过对该信号进行快速傅里叶变换(Fast Fourier Transform,FFT),得到反映结构信息的频谱图,最后对频谱图分析来判断结构的内部质量情况。
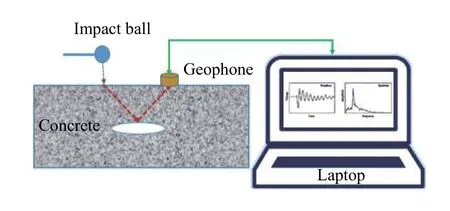
图1 冲击回波法基本原理Fig.1 Principle of impact echo method
但是,在实际的检测过程中很难得到理想的纵波反射信号,通常伴有干扰信号如面波干扰、随机噪声以及体波散射等[3-4]。为了解决这一问题,学者提出了不同时频分析方法,如短时傅立叶变换、连续小波变换及Hilbert-Huang 变换(HHT),来对冲击回波信号进行分析和研究[5-7]。这些分析方法中,HHT 相对于短时傅立叶变换和连续小波变换能获取更高的频率分辨率。集成经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)是HHT 过程中的关键步骤。但是,EEMD 通过加入高斯白噪声消除模态混叠问题,却带来了残余噪声的影响,导致分解出的IMF 不是唯一,而加总平均又增大了相应的计算成本[8-11]。为消除EEMD方法的局限性,Torres 提出了一种对噪声有自适应分解特性的完备集成经验模态分解(Complementary Ensemble Empirical Mode Decomposition,CEEMD),该方法效果明显好于早期的EEMD方法[12-13]。
针对传统方法对冲击回波信号分析的局限性,本研究将CEEMD 引入冲击回波信号分析,建立基于CEEMD 的冲击回波分析方法,通过仿真与试验证明研究CEEMD 对冲击回波信号分解后频谱特征和有效信号提取性能,为实际的冲击回波检测方法提供工程参考。
1 方法原理
1.1 冲击回波原理
冲击回波法对混凝土结构缺陷处反射信号的有无及强弱来识别缺陷的存在,入射弹性波的反射率越高检测的分辨率就越高。
根据弹性波传播理论,弹性波在遇到不同介质的交界面时,会发生反射和折射现象。对于双层介质,当弹性波从介质1 传播到介质2 时,其反射率 R计算式为:

式中: z1、 z2分别为介质1、介质2 的波阻抗,对于弹性波而言, z =ρv( ρ为 介质密度, ν为波速)。
对于夹层介质的情况,如图2 所示,反射率计算式为:
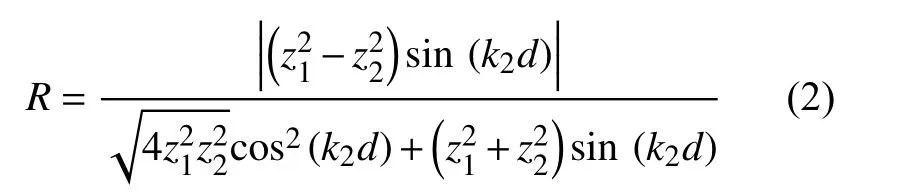
式中: k2为 介质2 中的波数, f 为频率, d为中间层厚度。
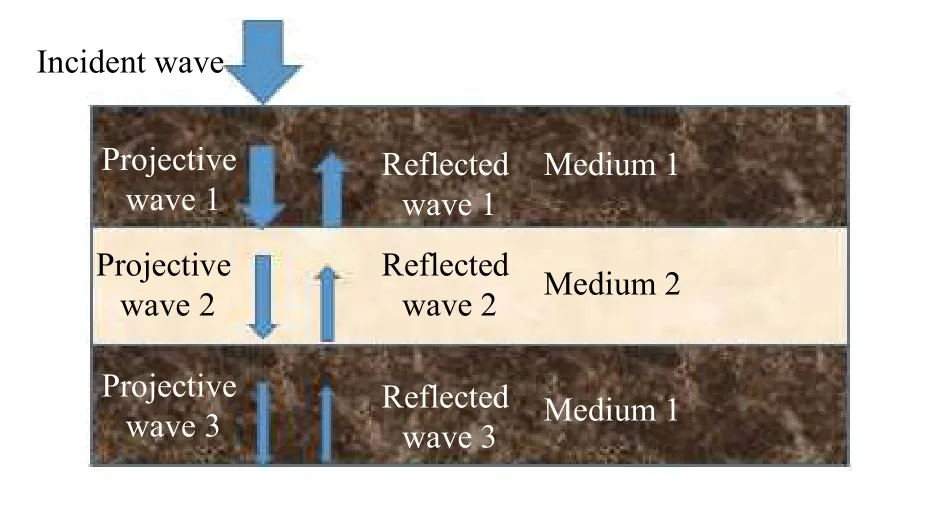
图2 介质含夹层时弹性波的传播与反射Fig.2 Elastic wave propagation and reflection in the medium sandwich
冲击回波测试结构厚度是通过回波信号最大峰值的频率来计算的,混凝土结构底板厚度或缺陷位置有下列关系式:

式中:D 为底板厚度或缺陷位置,Vp为纵波波速,f 为最大峰值频率,β=0.96 为经验校正系数。
1.2 冲击回波CEEMD 方法
CEEMD 方法在EEMD 的基础上进行改进,是一种自适应信号分解方法,有效地解决了EMD方法存在的分解不稳定、模式混叠和端点效应等问题。CEEMD 方法基本原理利用添加一对振幅相同、相位相反的高斯噪声来降低噪声残余,方法实现流程(图3)如下:
首先,将振幅相等、相位相反的n 组辅助高斯噪声加入原始冲击回波信号中,从而产生2 个集合IMF:
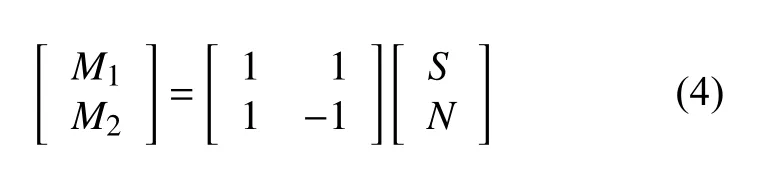
式中:S 代表原始信号,N 为高斯噪声,M1、M2加入噪声后的正负对信号集合。
其次,对集合 M1和 M2中所有信号进行EMD分解处理,分解后得到2 组集成的IMF 分量,即IMF1 和IMF2,IMF1 为正噪声组集成的平均结果,IMF2 为负噪声组集成的平均结果。
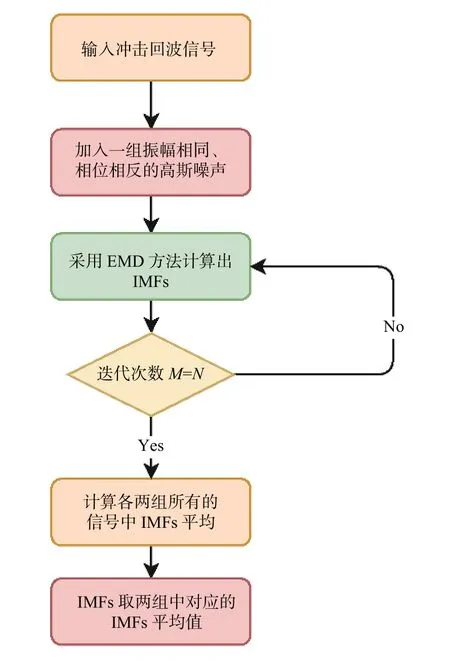
图3 CEEMD 方法冲击回波信号分解流程图Fig.3 Decomposition flow chart of CEEMD
最后,算法分解为2 组IMF 分量,对IMF1、IMF2 集成平均,结果为:
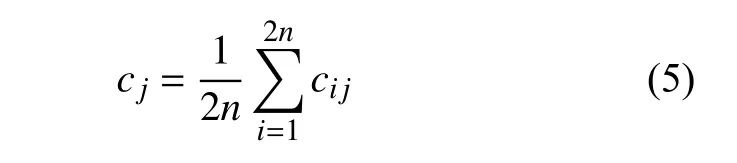
式中:cj代表CEEMD 分离得到的第j 个IMF 分量,cij为i 信号分离所得的编号为j 的IMF 分量。
CEEMD 方法通过在冲击回波原信号中加入正负对白噪声,消除了后期进行信号重构时出现的残余辅助噪声,不仅继承了EEMD 方法的优点同时提高了计算效率,而且减小了添加辅助白噪声带来的重构误差[14]。
2 冲击回波检测信号分析
2.1 冲击回波模拟信号分析
设计的仿真模型尺寸为200 mm×200 mm×20 mm 的混凝土板,在板内部有一尺寸为30 mm×30 mm×16 mm 夹层空隙(图4a)。模拟中计算参数混凝土密度为2500 kg/m3,弹性模量为37.8 GPa,泊松比为0.2[15]。相应的夹层和底部的回波的频率分别为12.3、9.8 kHz。利用有限元方法对该混凝土板冲击回波检测模拟,模拟出的冲击回波信号如图4b 所示。
根据图4 中的冲击回波信号,利用本研究提出的CEMMD 方法对冲击回波信号进行分析,将原始信号分解为相应的IMF,原信号分解后的结果见图5。
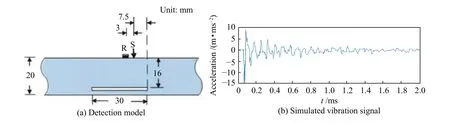
图4 冲击回波模拟试验Fig.4 Impact echo simulation testing
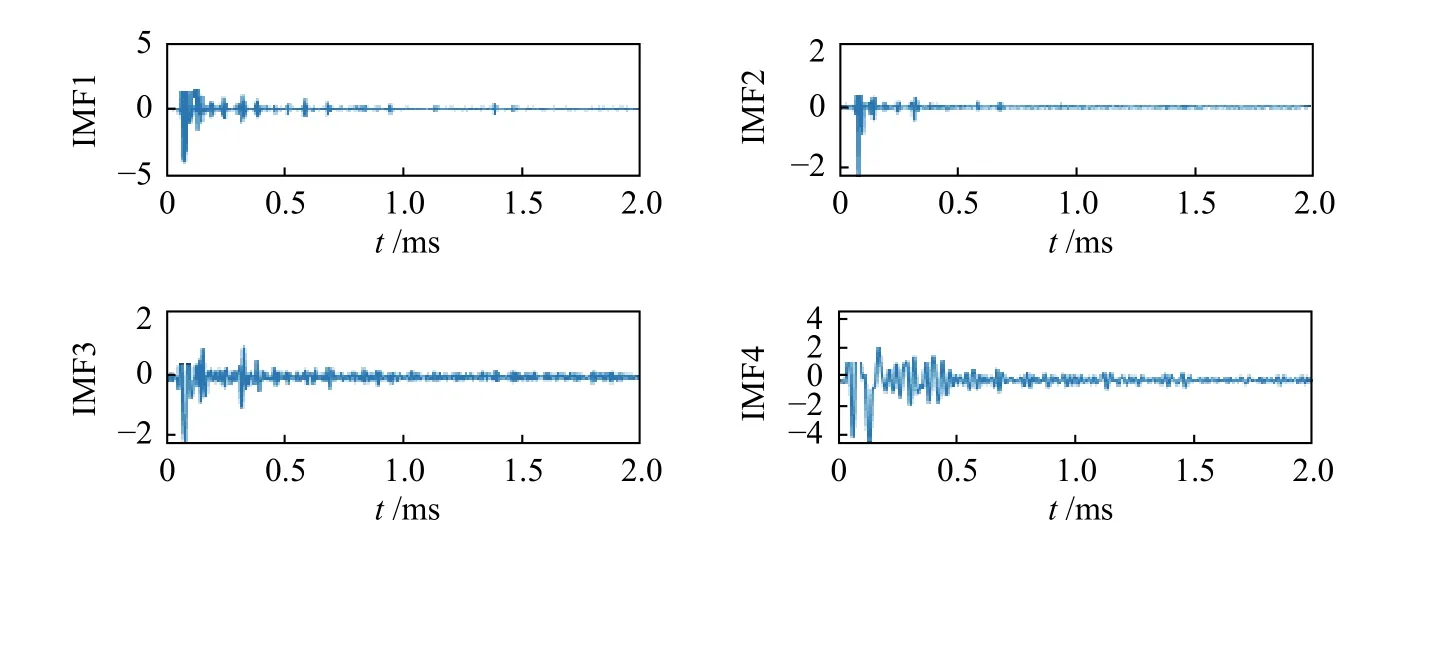
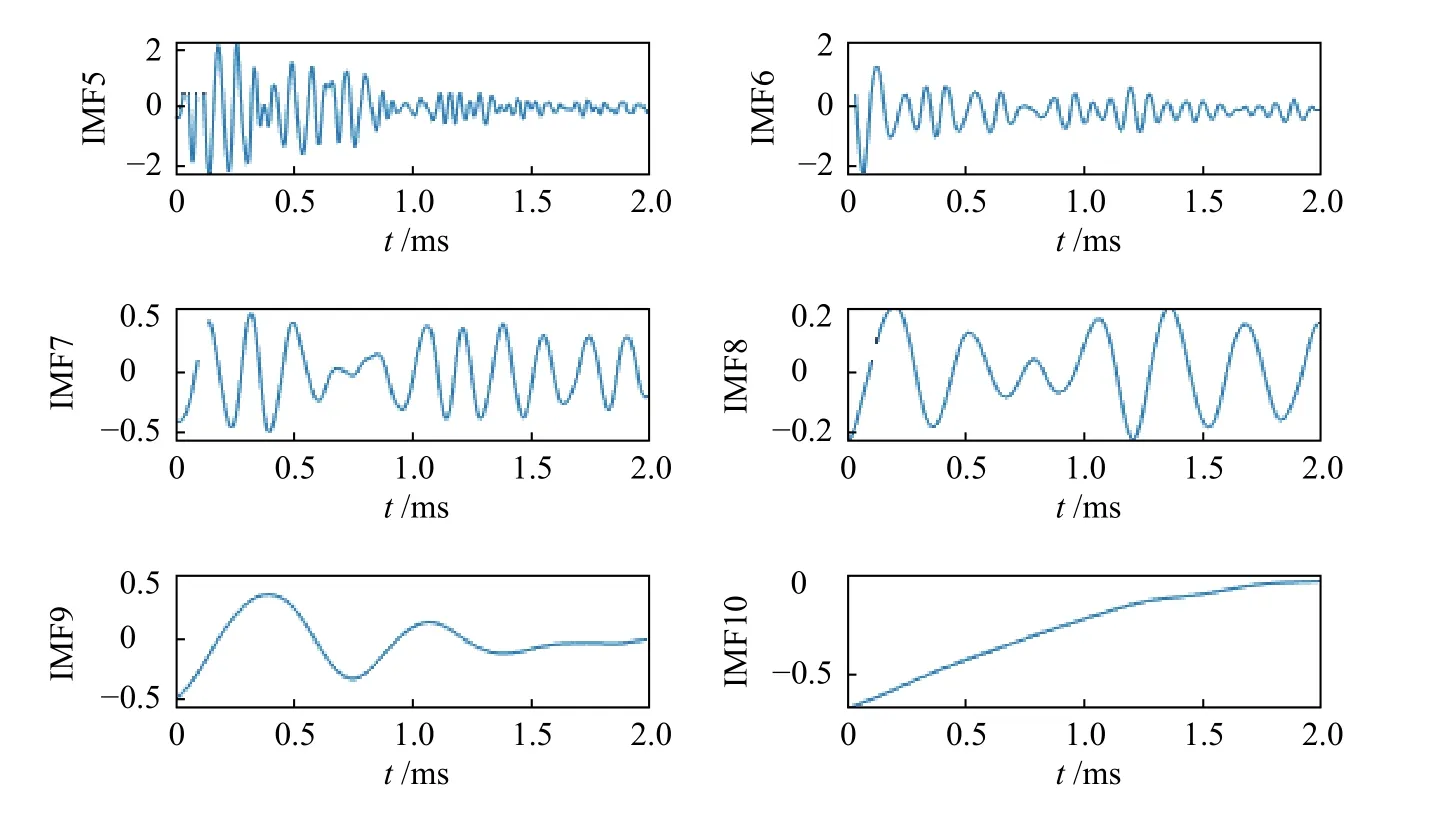
图5 CEEMD 分解冲击回波模拟信号的IMFFig.5 IMF decomposed on impact echo simulation signal by CEEMD
根据图5 结果,CEEMD 方法能够将原始冲击信号分解为不同的IMF,模态函数IMF1~IM10。从IMF1~IMF10 特征来看,模态函数振动频率排序逐渐减小,其中,IMF1~IMF4 主要以高频为主的成份,IMF5~IMF10 反映了冲击回波信号结构振动特征,IMF1~IM10 频率特征如图6 所示。
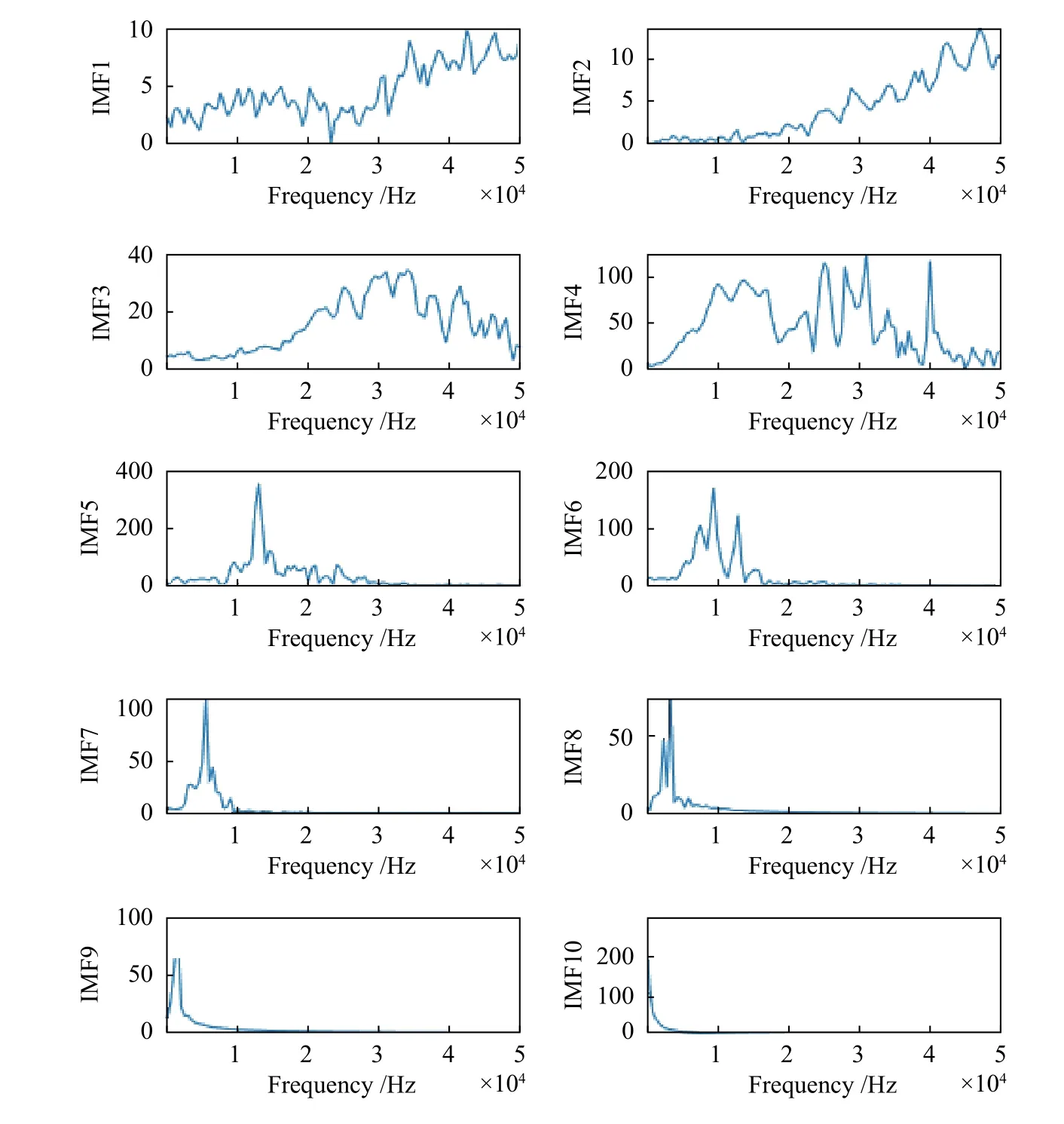
图6 冲击回波模拟信号的IMF1~IMF10 频谱图Fig.6 IMF1~IMF10 spectrogram on impact echo simulation
图6 的结果显示,IMF 能够很好与冲击回波信号特征相吻合。IMF1~IMF4 主要体现的是振动冲击回波信号高频成份。而IMF5、IMF6 对应的峰值频率分别为12.3、9.8 kHz,该频率是来自夹层空隙和板底反射信号的频率;由此可见,CEEMD方法能够很好地将板底和夹层空隙处的缺陷很好分离出来,并能对缺陷位置进行确定。
2.2 冲击回波工程检测信号分析
以美国弗吉尼亚州Gainesville 15 号公路的冲击回波现场测试为例(图7a),现场检测过程中检测位置进行了钻孔取芯,芯样如图7b 所示[15]。芯样路面面层厚度为21.6 cm,面层纵波波速大约为4000 m/s,由厚度和频率的关系式(3),计算得到底部反射波频率为9 kHz。但由于面波和噪声干扰,图7a 中的检测信号的频谱很难识别出底面的反射波频率。
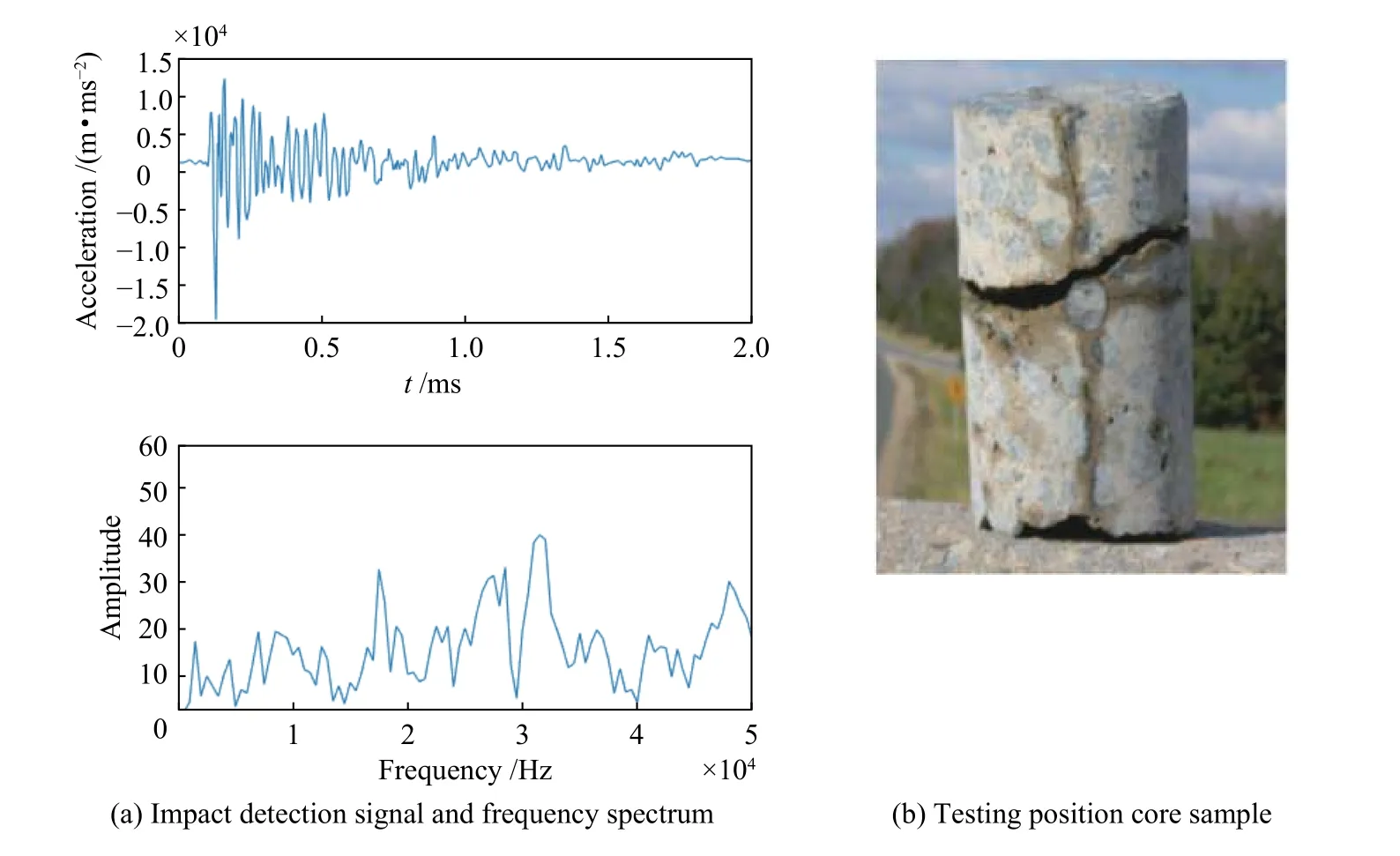
图7 冲击回波现场试验Fig.7 Impact echo on site testing
对该现场检测的冲击回波信号采用CEEMD方法进行分析,将该检测信号分解为相应的IMF,原始信号分解后的结果见图8。
根据图8 结果,CEEMD 方法能够将原始冲击信号分解为IMF1~IM10 特征模态函数。从IMF1~IMF10 特征来看,模态函数振动频率排序逐渐减小,其中IMF1~IMF4 主要以高频为主的成份,主由噪声信号和干扰信号组成。IMF5~IMF10 反映了冲击回波信号结构振动特征,IMF7~IMF10 成分为单调函数为主,与上节仿真冲击回波信号的分析结果一致。对IMF1~IM10 特征模态函数进行频谱变换,其频率特征如图9 所示。
图9 显示出IMF1~IM10 特征模态函数变化规律,IMF1~IMF4 主要体现的是振动冲击回波信号高频成份,是由噪声和面波干扰形成的高宽频信号。而IMF5、IMF6 对应的峰值频率分别为17.5、9.0 kHz,可判断出该频率是来自夹层空隙和底面反射信号形成。根据频率与厚度的函数关系式(3),脱空位置在10.5 cm 处,图7b 中芯样脱空位置大致在10.0 cm 附近;而底面反射波峰值频率也为9.0 kHz,与实际情况相符。由此可见,冲击回波信号受干扰波影响时,CEEMD 方法能正确识别出结构中的缺陷位置和混凝土厚度。
3 结论
1)CEEMD 方法能够有效地将冲击回波信号从含有严重的面波和噪声干扰中分解为相应的IMF 分解为相应的IMF,IMF 模态函数频率由高到低按序排列。
2)IMF 对应的频谱显示,高频成份一般为噪声干扰成份为主的面波信号,处于中间的IMF 则为夹层处缺陷和板底反射成份的信号。
3)分析缺陷和板底反射信号的对应IMF,确定缺陷和板底反射信号频率,再由频率准确计算内部夹层缺陷位置和混凝土板厚。
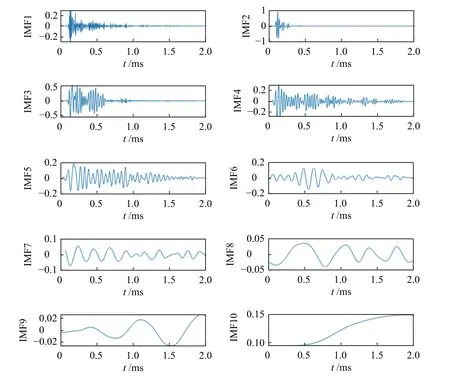
图8 CEEMD 对现场测试信号分解的IMFFig.8 IMF decomposed on site testing by CEEMD
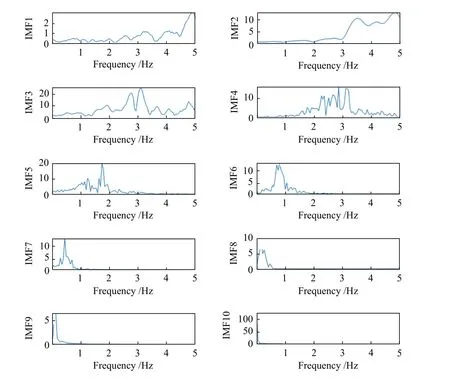
图9 现场检测信号的IMF1~IMF10 频谱图Fig.9 IMF1~IMF10 spectrogram on site testing signal
