五轴加工中奇异问题分析及优化方法

洪欣宇,洪荣晶,林晓川

(1.南京工业大学 机械与动力工程学院,江苏 南京 211800; 2.江苏省工业装备数字制造及控制技术重点实验室,江苏 南京 211899)

在实际生产中,五轴机床常用于曲面较复杂的零件加工。五轴机床虽然提高了零件的加工质量,但同时也带来了一系列问题,Zlatanov等[1]提出当零输出的机床存在非零输入时,即发生加工奇异问题。该问题易造成表面加工轨迹不光顺,甚至产生干涉和擦伤[2]。五轴加工中发生奇异问题的区域通常与该机床的运动相关,因此每个五轴机床都有一个造成冗余输入的奇异点。当在奇异区域内进行加工时,为了获得恒定的切削进给速率,机床轴运动会发生突变。

关于奇异问题优化的研究主要分为3类:① 在CAD/CAM建模阶段对奇异区域内刀具轨迹进行调整。但该类方法可能会引起新的误差。Affouard[3]基于旋转轴运动的最小增量和定位精度,提出了用于规避奇异点的奇异锥体(singular cone)概念。Yang等[4]通过旋转位于奇异锥体内的刀轴矢量来进行优化,但旋转角度过大会导致加工精度降低。Lin等[5]将奇异区域内的刀轴矢量整体进行平移,从而避开奇异锥度圆，但该方法不适用于侧面铣削,经优化后采用粒子群算法来计算最佳平移向量,改善了加工工件的表面纹理[6]。② 在后处理阶段进行优化。但该类方法可能会造成机床轴的运动速度发生突变,对伺服电机和机床床身产生损坏。Srby[7]通过修改靠近奇异点的逆运动学矩阵进行优化。Boz等[8]通过调整旋转轴变量大于90°时的主旋转轴角度来规避奇异点。王峰等[9-11]提出基于雅可比矩阵的奇异区域检测和处理方法,修改了奇异点附近的刀轴矢量。③ 在实际切削阶段进行优化。但该类方法受限于刀具轨迹的特定形状。Anotaipaiboon等[12]和Pessoles等[13]通过改变工件配置来提高加工效率和避免奇异问题。Cripps等[14]指出奇异区域与旋转工作台的系数有关,还提出通过利用特殊设计的夹具重新定位工件来解决奇异问题。

因此,对于五轴加工中的奇异问题,通常在刀位数据生成阶段进行调整,避免与设计模型本身产生较大误差[15]。国内还有部分学者通过分析刀具运动的非线性误差来提出优化方法,文献[16-18]通过分析旋转轴运动过程中线性插补引起的刀具偏差角,限制相邻刀轴矢量的夹角来进行误差控制。耿聪等[19-20]在此研究基础上采用等幅旋转法对旋转轴坐标值进行优化。笔者通过分析影响旋转运动误差的相关变量,结合旋转变化率(R)提出一种奇异问题优化方法，并以叶轮流道表面加工为例,验证该方法的可行性。

1 旋转运动引起的奇异问题

五轴机床中的旋转运动轴能够提高各种复杂曲面加工的灵活性,但也会造成奇异问题。五轴加工中实际加工轨迹与理想刀具轨迹的不同会对表面质量和机床本身性能产生影响。笔者以AC式摆头/转台回转型五轴机床为主要研究对象,分析其加工时的旋转运动轨迹,并研究产生奇异问题的原因。

1.1 五轴机床运动模型

AC式五轴机床结构如图1所示。由于工件在工件坐标系中坐标位置与在机床坐标系中不同,因此将工件坐标系中的刀位点和刀轴矢量经过转换后,生成机床坐标系中各轴的运动坐标。图1中机床的正向运动链依次为刀具、A轴旋转、Y轴、Z轴、X轴、机床床身、C轴旋转和工件。依照运动链转换后得到工件坐标系下刀轴矢量Nk如式(1)所示。

(1)

式中:θA和θC为机床坐标系下A、C旋转轴的运动角度,Nkx、Nky和Nkz分别为工件坐标系下x、y和z轴的刀轴矢量坐标。

图1 AC式摆头/转台回转型五轴机床Fig.1 AC-type five-axis machine of tool and table separated rotation

机床坐标系下A、C旋转轴运动坐标与刀轴矢量关系如式(2)所示。

(2)

1.2 五轴加工中奇异问题分析

如图2所示,以某两个相邻刀轴矢量Nk1到Nk2运动为例,图2中，Nkp为理想运动中某时间点的刀轴矢量；N′kp为实际加工中相应时间点的刀轴矢量；δ为Nkp和N′kp之间的误差；α为Nkp和N′kp之间的误差角；λ为Nk1与Nk2之间的夹角；tλ为Nk1与Nkp之间的夹角；t为单位时间，t∈[0, 1]。当δ过大时，不仅会对表面加工质量产生影响,还会造成奇异问题。因此,通过计算相邻刀轴矢量间的最大刀轴误差角αmax,并分析各变量对奇异问题的影响,从而提高加工表面质量。

图2 相邻刀轴矢量间的运动轨迹Fig.2 Movement between adjacent tool orientations

运用四元数球面法表示理想运动中某时间点的刀轴矢量Nkp，如式(3)所示。

(3)

根据式(2),得到实际加工中相应时间点的刀轴矢量N′kp，如式(4)所示。

N′kp(t)=-cosθA(t)sinθC(t)-

cosθA(t)cosθC(t)-sinθA(t)

(4)

刀轴误差角α如式(5)所示。

(5)

式中：θA1和θA2分别为Nk1和Nk2的A轴运动角度，θC1和θC2分别为Nk1和Nk2的C轴运动角度，U为中间量。

由式(5)得,当U(t)求得最小值时,α(t)也可求得最大值,即δ为最大值。通过对U(t)关于t求导,得出当t=1/2时,dU(t)/dt接近于0。所以当刀具运动至相邻刀轴矢量中间位置时,α(t)最大,则δ也达到最大值[17]。

在t值确定后,式(5)可简化为式(6)。

(6)

式中,ΔθA和ΔθC分别为A、C轴运动角度变化量。

λ在实际加工中如式(7)所示。

cosλ=Nk1·Nk2=cosθA1sinθC1cosθA2sinθC2+

cosθA1cosθC1cosθA2cosθC2+sinθA1sinθA2=

cosθA1cos(θA1+ΔθA)cos ΔθC+

sinθA1sin(θA1+ΔθA)

(7)

因此,得出α(t=1/2)如式(8)所示。

(8)

由式(8)可得出,由α过大而导致的奇异问题与变量ΔθA、ΔθC和θA1的取值有关。

1.3 旋转变化率对奇异问题的影响

从式(8)很难观察出变量ΔθA、ΔθC和θA1取值对α(t=1/2)的直接影响,因此利用控制变量法对α进行数值化分析,探讨各变量对α的影响,如图3—5所示。其中,为了避免式(8)中一些特殊角度取值对结果产生误差,也为了更好地观察ΔθA和ΔθC之间变化关系对α的影响,引入了旋转变化率R这一概念。旋转变化率指五轴加工中两个旋转轴在同一时间运动角度变化量之间的比值,如式(9)所示。

(9)

由于该机床A轴运动角度取值范围通常为-90°～0°,θA1分别取值-60°、-45°和-30°进行对比(图3)。θA1的变化对α影响不明显,且实际加工中θA1取值和曲面零件模型本身有关,改变θA1可能会造成整体走刀运动的较大变化而造成新的加工误差,甚至产生碰撞干涉问题。

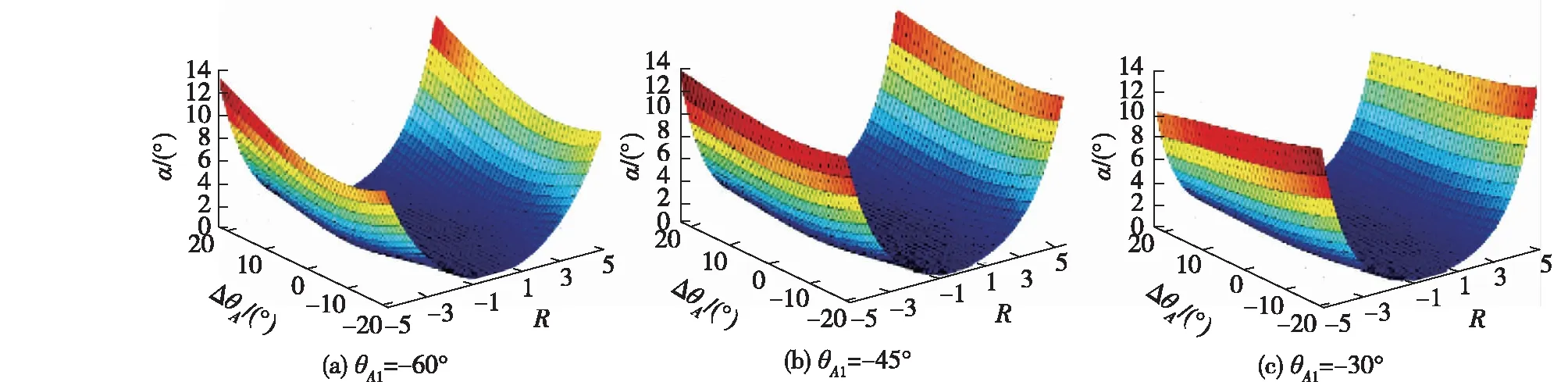
图3 R和ΔθA对α的影响Fig.3 Effects of R and ΔθA on error angle α

图4 R和θA1对α的影响Fig.4 Effects of R and θA1 on error angle α

图5 ΔθA和θA1对α的影响Fig.5 Effects of ΔθA and θA1 on error angle α

由图4和5得出:ΔθA绝对值越大,α越大。所以在对奇异问题进行优化时,要缩小ΔθA的范围。R绝对值越大,α越大。当R>2时,α数值变化图像会产生两个波峰(图5(c))。

综上可以得出:R和ΔθA绝对值过大是使α过大的主要因素,也同样会导致加工中的奇异问题。

2 五轴加工奇异问题优化方法

对于五轴加工中旋转运动的奇异问题,笔者提出的优化方法如下:对相邻刀轴矢量坐标进行调整,控制A轴运动角度变化量的绝对值|ΔθA|小于其限定最大值ΔθAmax(ΔθAmax>0),同时缩小旋转变化率的绝对值|R|。该方法同样也能对两个旋转轴的运动角度变化量ΔθA和ΔθC取值范围进行限定。

2.1 刀轴矢量的坐标转化

在刀位数据中,刀轴矢量Nk通常为一个三维单位向量,其坐标为 (Nkx,Nky,Nkz)。如图6(a)所示,Nk的定义:将刀轴矢量Nk放置在一个单位球中,其中起始坐标设定为单位球球心,末端坐标(Nkx,Nky,Nkz)为在单位球表面的取值[5]。因此,根据AC式摆头/转台回转型五轴机床运动特点,刀轴矢量沿单位球同一纬度线的运动相当于在C轴的运动变化,则刀轴矢量沿单位球同一经度线的运动相当于在A轴的运动变化。如图6(a)所示,在实际加工中刀轴矢量Nk1到Nk2的运动为刀具围绕A轴的摆动,刀轴矢量Nk2到Nk3的运动为转台围绕C轴的转动。

若直接将刀轴矢量在空间中进行旋转变换,不仅计算过程较复杂,对ΔθA和R的控制也比较困难。因此，需要将刀轴矢量转化到平面中进行优化。如图6(b)所示,选取平行于xOy的平面,将单位球中三维向量转化为平面单位圆中的二维向量坐标。则刀轴矢量Nk1到Nk2在二维坐标中沿圆径向的运动相当于在A轴的运动,刀轴矢量Nk2到Nk3沿圆周向的运动相当于在C轴的运动。具体向量坐标转化的操作:将刀轴矢量Nk的三维坐标整体除以z轴坐标Nkz,转化为(Nkx/Nkz,Nky/Nkz,1);由于z轴坐标相同,所以刀轴矢量Nk坐标转化为二维坐标(Nkx/Nkz,Nky/Nkz),记为Nk(x,y)。

图6 刀轴矢量的坐标转化Fig.6 Coordinates transformation of tool orientations

式(2)中的A、C旋转轴运动角度坐标如式(10)所示。设l=x2+y2,A轴运动角度坐标与l有关,C轴运动角度坐标与x/y有关,该验证结果与图6(b)中描述一致。

(10)

2.2 奇异问题优化方法

图7 改变刀轴矢量坐标优化RFig.7 Changing the coordinates of tool orientations to optimize R

3 实验验证

运用针对奇异问题的刀轴矢量优化方法,以直径为100 mm的八叶片叶轮为例,优化叶片间流道的加工表面。在二维坐标平面内对刀轴矢量进行旋转调整,缩小旋转变化率R,最后进行加工试验验证。

如图8所示,将叶轮流道内刀轴矢量用点表示。图8中,蓝色点表示刀轴矢量的旋转变化率R小于限定值,红色点表示待优化的刀轴矢量。为了更加直观地分析旋转变化率R与奇异区域的联系,取值范围依次为R<15、R<10、R<5和R<2。图8中R取值越小,红色点面积越大,需要优化的刀轴矢量也越多。红色点主要集中在叶轮流道与叶片交界处,该部分表面曲率变化较大,因此旋转轴运动角度变化量也较大,容易产生奇异问题。

图8 叶轮流道刀轴矢量的R分布点图Fig.8 Point distribution diagrams of R of tool orientations in impeller passage

将优化后不同R取值范围内的刀位数据转化为机床坐标,分别在五轴机床上进行加工。主轴转速为3 000 r/min,进给速度为200 mm/min,切削深度为0.1 mm。图9为在不同旋转变化率取值范围下,经过表面加工后同一处的叶轮流道表面局部放大图,其中R取值范围越大,表面呈现的轨迹中奇异问题越明显,表面质量也越差。

图9 表面加工后叶轮流道表面局部放大图Fig.9 Local enlarged views of the machined surface of impeller passage

采用粗糙度测量仪分别对加工表面进行测量,得出轮廓算术平均偏差(Ra)、均方根粗糙度(Rq)、轮廓峰谷最大高度(Rz)、轮廓最大的高度(Rt)、最大的峰值(Rp)和最大的谷值(Rv)，具体测量数据如表1所示。当旋转变化率R<15时,Ra、Rq和Rz的两次测量平均值分别为2.496、3.157和6.396 μm,在4组测量中数据最大;R<2时,Ra、Rq和Rz两次测量平均值分别为0.970、1.224和4.535 μm,在4组测量中数据最小。从表1中的测量数据还可以得出:R取值范围越小,表面粗糙度越小,加工表面质量也有所提高。

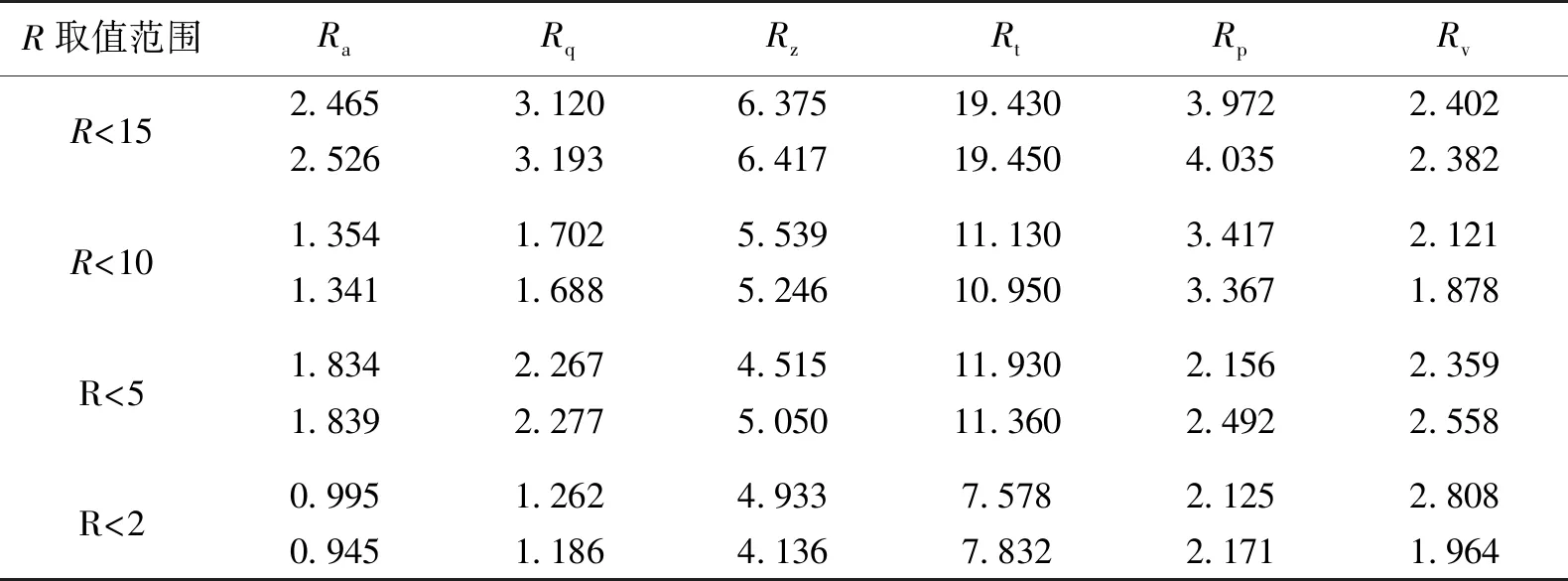
表1 局部叶轮流道表面粗糙度

4 结论

1) 通过分析相邻刀轴矢量间的旋转误差角,并观察不同变量对其的影响,探讨五轴加工中奇异问题产生原因。结合旋转变化率R提出了一种奇异问题的优化方法,并在刀位数据生成阶段调整刀轴矢量来减小R,从而控制旋转误差角,提高表面加工质量。

2) 以叶轮流道为实验加工对象,验证该优化方法的可行性,并对加工表面的粗糙度测量数据进行对比,证明旋转变化率R较大时易产生奇异问题。

3) 笔者所提出的优化方法是在A轴旋转运动角度变化量ΔθA不变的基础上,结合R取值范围对刀轴矢量进行调整,因此可以直接有效运用于自由曲面的工业制造。