基于反义RNA膜计算的欠驱动桥式吊车最优消摆控制

2021-01-21杨世品许云辰李丽娟薄翠梅

南京工业大学学报(自然科学版) 2021年1期

杨世品,许云辰,李丽娟,薄翠梅,徐启

(南京工业大学电气工程与控制科学学院,江苏南京 211800)

欠驱动系统作为一类驱动器个数少于系统自由度的系统,仅通过较少的控制量可实现更多状态量的控制,控制难度非常大[1]。桥式吊车是一种典型的非线性欠驱动系统,由于其负载能力强、操作灵活而被广泛应用于车间、仓库、码头等重要工业搬运场所。桥式吊车系统的主要控制目标为对负载的快速、准确“点对点”搬运,然而由于吊车搬运系统的欠驱动特性、吊车的加减速和外界各种干扰,桥式吊车在吊运过程中负载极易发生大幅摆动的现象[2-3]。该现象不仅严重影响了负载的定位精度,而且还降低了桥式吊车的吊运效率,给实际工业生产带来了货物碰撞、损坏和人员伤害等不安全因素[4]。基于这一特性,桥式吊车系统消摆控制问题的研究受到了控制领域学者们的广泛关注。

通过对桥式吊车系统的合理建模,利用计算机仿真手段,结合各种控制策略,可对桥式吊车系统的消摆控制进行预测,性能良好的控制模式可作为实际桥式吊车精准位移下快速消摆的理论依据,其形成的自动搬运技术可显著地提高桥式吊车系统的工作效率。从稳定及抗扰角度出发,国内外学者提出了一系列的闭环控制方法,例如有限时间控制[2]、最优控制[5]、部分状态反馈控制[6]、输出反馈控制[7]、模糊控制[4,8]、跟踪控制[3,9]、最优比例积分微分(PID)闭环控制[10]、滑模控制等[11-13]。文献[2-13]表明:这些策略在非线性严重的桥式吊车快速消摆过程中均有一定的控制效果。但无论采用何种控制器,其控制参数的整定都十分棘手,大量人工试凑的控制器参数往往不能使得该类欠驱动桥式吊车在到达指定位置后吊绳摆动在尽可能短的时间内消除。近年来的一系列研究成果表明,利用智能优化算法获取控制器参数是最有效的途径之一[14-15]。

众所周知的智能优化算法如遗传算法(GA)、蚁群算法(AA)、粒子群优化(PSO)、神经网络(NN)、DNA计算、进化计算(EC)等已被用于解决实际中的各种优化问题[16]。但在生物界的遗传、神经网络、免疫系统、生命个体和生物群体中,生命不仅仅是以神经网络这种结构形式存在,也不只是以DNA分子这种遗传物质形式存在,更不仅仅是以群体的形式存在,更准确地说它是以细胞为基本单元的有机整体。而作为生命基石的细胞,在长达几十亿年的进化中必然保留了很多非常优秀的行为,但是早些时候,这一具有复杂结构的精妙“机器”却被研究人工智能的学者们忽略了[16]。基于对生物体内细胞膜生命进程的研究,欧洲科学院院士、罗马尼亚科学院院士Pǎun[17]于1998年在芬兰图尔库计算机中心的研究报告中首次提出了“膜计算(MC)”的概念,它是一个从生命细胞以及由细胞构成的组织和器官的结构和功能中抽象出来的计算模型。文献[16]表明:膜计算在系列复杂优化问题处理中较传统的智能优化算法具有更高的搜索精度和更快的收敛速度。

然而,传统的膜计算只是对生命细胞的结构和功能的简单模拟,细胞作为生命活动的场所也并非只进行物质和能量的简单交换以及细胞核内遗传信息DNA→RNA→蛋白质的单一复制和翻译。值得一提的是,除了众所周知的一类遗传物质及活动,反义RNA(aRNA,与信使RNA互补的RNA分子)引起了越来越多科学家的关注和重视。反义RNA最早在原核生物中被发现,最新研究发现真核生物中也存在反义RNA,其在抑制与疾病发生相关基因的表达调控过程中意义非凡[18], 但这一重要概念在众多的膜计算优化算法中鲜为报道。

受反义RNA对细胞内基因表达调控的启发,笔者提出一种新型的基于反义RNA膜计算(aRNA-MC)的优化算法,以欠驱动桥式吊车最优消摆控制器的设计为目的,通过所提算法分别对桥式吊车消摆控制中经典的PID控制器和滑模控制器的参数难以整定这一实际问题进行针对性地解决。

1 问题描述

1.1 欠驱动桥式吊车数学模型

一个理想的二维桥式吊车系统模型如图1所示。吊车在控制力作用下沿桥架水平移动,其带动吊绳对负载进行牵引直至运送到目标位置。根据拉格朗日法,对桥式吊车进行建模,数学模型如式(1)和(2)所示[11-12]。

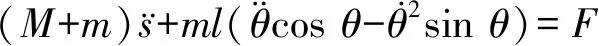
(1)

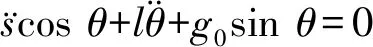
(2)

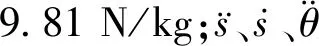
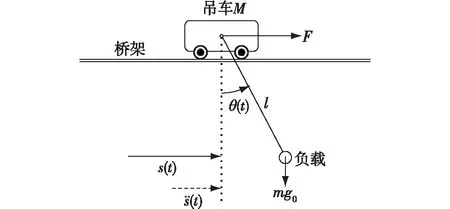
图1 欠驱动桥式吊车系统模型Fig.1 Under-actuated overhead crane model

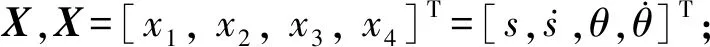
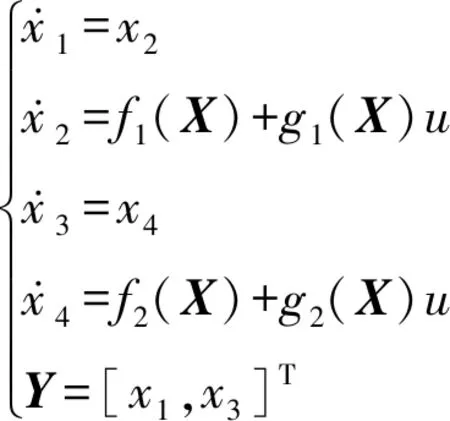
(3)

式中:f1(X)、f2(X)、g1(X)、g2(X)均为非线性函数,表达式分别如式(4)—(7)所示。

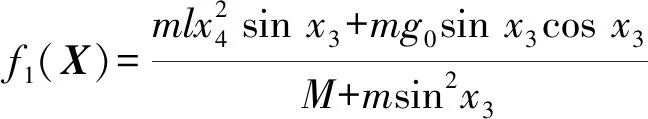
(4)

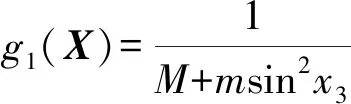
(5)

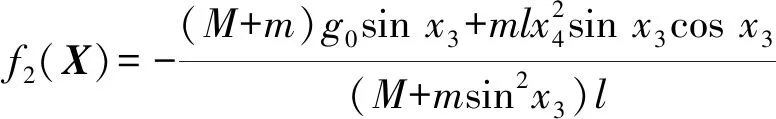
(6)

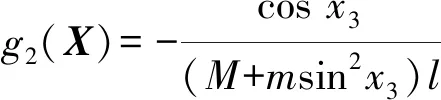
(7)

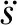
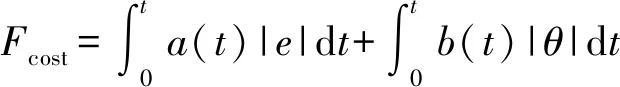
(8)

式中:Fcost为期望最小化的指标;t为仿真时间;e为吊车期望位置sd和实际位置s的误差,e=sd-s;a(t)和b(t)分别为位置误差和摆角的权值。

1.2 消摆控制策略

1.2.1 PID控制

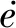
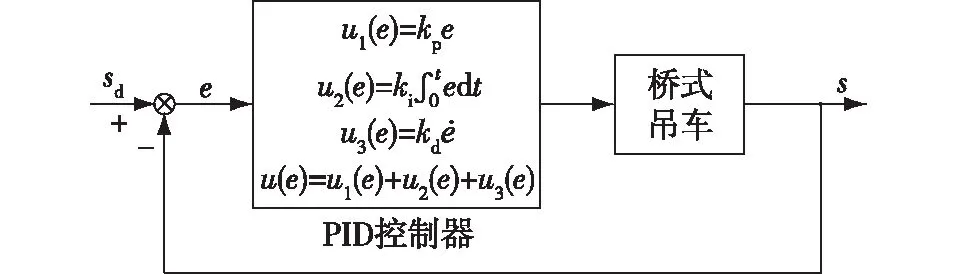
图2 桥式吊车位置PID控制系统框图Fig.2 Block diagram of position PID control for overhead crane

由图2可知:位置PID控制器的输出直接作为吊车的控制信号对吊车进行控制,由于吊车位移s和吊绳摆角θ互相耦合,但图2中并无专属的摆角抑制控制规律,如何对PID控制器的参数进行整定同时实现吊车准确定位和吊绳摆角迅速消除具有很高的难度。针对PID控制器的3个重要参数kp、ki、kd的各种组合,只需要使式(8)的评价函数数值最小,获得3个最优可调参数,即可实现该非线性欠驱动强耦合桥式吊车系统准确定位下的快速消摆。

1.2.2 滑模控制(SMC)

滑模控制作为一种变结构系统,其在控制的动态过程中可根据系统当前的状态(如偏差及各阶导数等)有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运行,系统状态先从超平面之外向切换超平面收束,然后再沿切换超平面向原点滑动。研究表明,滑模控制对非线性系统具有良好的控制效果[5,11-12]。

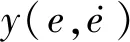
(9)

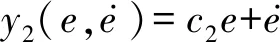
(10)

(11)

式中,c1、c2、λ1、λ2均为滑模控制器的可调参数。

基于综合切面函数的滑模控制器输出usw为

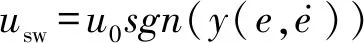
(12)

式中:u0为滑模控制器的增益因子,sgn(y)为y的符号函数。结合图3可知:只需要获得能使式(8)数值最小的5个最优参数值(c1、c2、λ1、λ2、u0),滑模控制器输出的控制力可尽可能地最优消摆。此外,鉴于这5个参数与usw之间的关系,可预置λ1=1,而仅调节其余4个参数以提高搜索效率。

图3 桥式吊车滑模控制系统框图Fig.3 Block diagram of sliding mode control for overhead crane

针对上述两种控制器的参数需要整定的情况,结合传统智能优化算法进行参数整定时容易造成局部最优而难以找到全局最优解这一问题[19],笔者在前人的工作基础上,设计了一种新型的生物启发式算法,即反义RNA膜计算(aRNA-MC)优化算法。

2 反义RNA膜计算优化算法

2.1 膜计算优化算法基本结构

膜计算作为一种从生命细胞以及由细胞构成的组织、器官的结构和功能中抽象出来的计算模型,在随机优化领域拥有巨大的潜力[16]。标准细胞型膜计算的分层膜结构如图4所示,除了表层膜外,其他膜均嵌在其临近的外层膜中。图4中,S为膜内的对象或优化问题的可行解;1, 2,…,L为膜的层数;表示优化进程中对象子集交流的方向。当表层膜内所有对象均更新完毕但不满足终止条件时,表层膜将向最内层膜直接与部分对象集进行交流。

膜计算优化算法可以用一个结构体Π形式化表示，如式(13)所示。

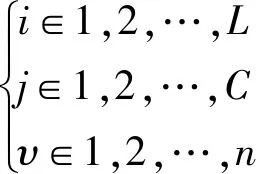
(13)

式中:V为字符表,表示一个非空的抽象字符集,对象都由字符集中的字符编码而成,如果系统中的对象都采用实数编码,则这些对象可直接看成某一问题的可行解;B为结构体中膜计算优化算法的最佳可行解,B⊂V;μi为第i层膜内的区域;Rij为第i层膜内第j个对象更新时采用的规则集;Sij=f(x1x2…xn)为对象,其中f为该对象对应某一待优化问题的适应度或目标函数值;ζυ为问题解的第υ维变量的搜索范围,ζυ=[xmin,υ,xmax,υ];C为每层膜内初始对象规模;n为待优化问题的自变量个数或维度。

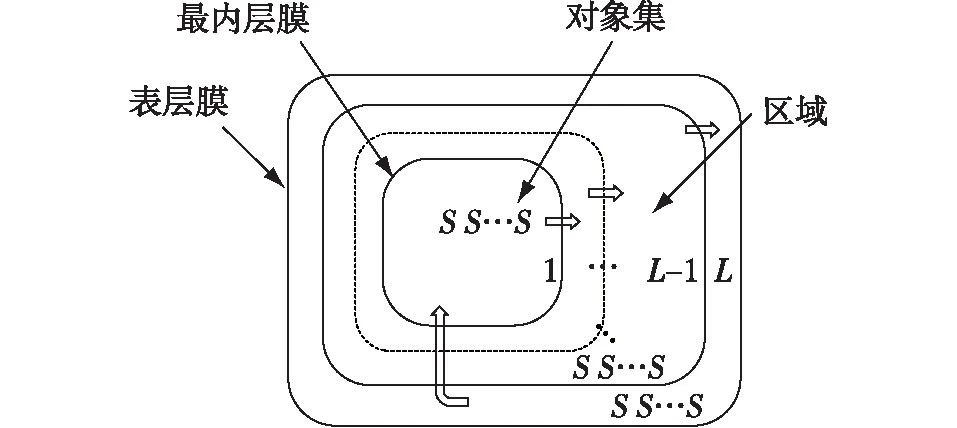
图4 标准细胞型膜计算的结构图Fig.4 Structure diagram of a standard cell-like membrane computing

膜计算中三大要素除了膜的结构、对象外,规则对膜计算的搜索性能至关重要,如何有效地使得算法既具有较好的全局勘探能力又具有非常好的局部搜索精度,是检验算法整体性能优劣的重要依据。除标准膜计算[16]中原有选择规则、交流规则、算术交叉规则、终止规则外,受细胞生命活动中反义RNA调控功能机制的启发,笔者设计了一种新型的反义RNA动态抑制规则。

2.2 反义RNA动态抑制规则

根据文献[18]的描述,反义RNA作为与靶RNA(多为mRNA)互补序列的RNA分子,其与靶RNA进行碱基配对结合的方式参与基因表达的调控。值得注意的是,这种低丰度、有特异选择性的反义RNA同样具有高效的阻抑效应,其在抑制一些有害基因的表达或失控基因的过度表达上具有重要的意义。膜计算优化算法也是对各层膜内对象不断地更新、选择、复制和交流的过程,而局部最优解的大量复制和聚集可被认为是一种有害或失控基因的过度表达。

为了抑制这种有害对象可能过早熟及算法易陷入局部最优的现象,膜计算优化过程中当前膜内对象集应选择性地参与到下一循环周期的更新操作中。同时,为防止过度抑制,考虑到算法前期应尽可能地跳出局部最优解,后期应搜索到精度尽可能高的解,抑制程度也应科学地动态调节。笔者所提出的反义RNA动态抑制规则如式(14)所示。

(14)

式中:x′v为对象Sij的第v维变量xv更新后的值;S′ij为动态抑制更新后的对象;f′为新对象S′ij的适应度；rand为区间随机实数函数；round为取整函数；Na为整型抑制阈值;pa为抑制率，是随优化进程动态变化的抗早熟抑制函数,pa变化曲线如图5所示;g为膜计算优化当前循环周期数;G为指定的最大循环周期数。

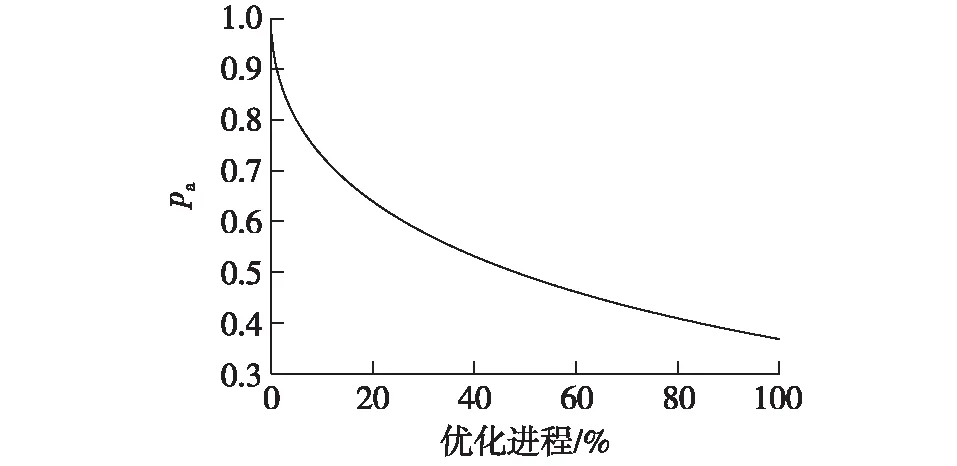
图5 反义RNA动态抑制率曲线Fig.5 Antisense RNA dynamic inhibition rate curve

为防止算法早熟,算法应更多关注搜索空间中对象集的大范围全局勘探,而非早期可能已陷入局部最优的个体集局部优化及复制。同时,也应对算法已找到的当前最优解进行部分保留。反义RNA动态抑制规则具体表述:设当前循环周期数为g, 第i层膜内所有个体均完成更新,执行i=i+1和j=1,并通过式(14)计算出当前抑制率pa和抑制阈值Na,针对i+1层膜内的C个对象,依据各自适应度函数值由大到小进行排序。前1～Na个对象保留,而余下C-Na个对象集则优先随机重分布,新组成的C个对象再进行逐个更新,这无疑增加了对象集更新过程中的多样性。但过多的重分布势必造成算法收敛速度下降以及对象集中有效信息的累积缺失,故在优化进程中,应适当逐步减小抑制率,使得算法在已实现全局勘探之后,将搜索重心逐步转移至全局最优解的精度提升(局部开采)上,但后期也不应只进行局部开采而忽视外部少量散点的作用。

由图5可知:在反义RNA动态抑制规则搜索进程中,pa从0.96逐渐降为约0.37,该动态抑制可同时兼顾算法初期的全局勘探和后期的局部开采。

2.3 反义RNA膜计算优化算法流程

反义RNA膜计算优法算法流程具体实现步骤如图6所示。

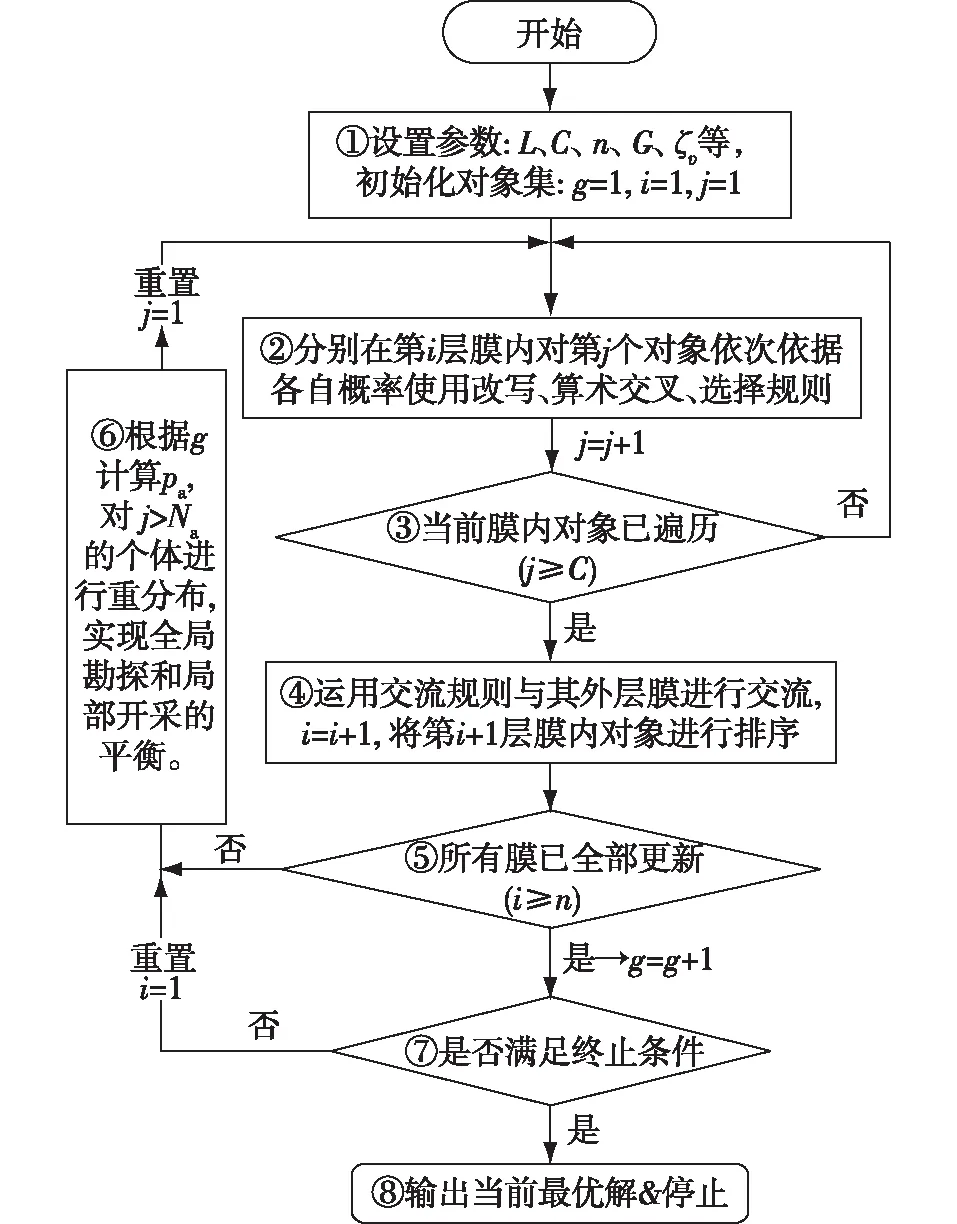
图6 反义RNA膜计算算法流程Fig.6 Flowchart of antisense RNA membrane computing

3 控制性能比较及结果分析

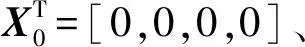
3.1 相同算法下不同控制策略的比较

欠驱动桥式吊车需同时满足负载的快速搬运和摆角的快速消除,鉴于式(8)中|e|和|θ|的量纲不同以及数量级的差异,笔者将同时选取文献[10]和[12]的权值作为测试平台。文献[12]中,a(t)=1、b(t)=2,即目标函数值是与时间无关的误差绝对值累积(IAE);文献[10]中a(t)=b(t)=t,该文献将两种误差的绝对值与时间的乘积作为累计项(ITAE)。通过比较和分析,发现文献[12]的IAE目标评价法倾向于桥式吊车运行及消摆的前期快速性,而文献[10]的ITAE目标评价法更倾向于桥式吊车运行及消摆的后期稳定性。为了实现不同控制策略和目标函数的交叉比较,基于反义RNA膜计算无时间参与IAE的PID最优控制实验表示为aRNA-MC-PID-NT;基于有时间参与ITAE的PID最优控制实验表示为aRNA-MC-PID-T;基于反义RNA膜计算无时间参与IAE的滑模最优控制实验表示为aRNA-MC-SMC-NT；基于有时间参与ITAE的滑模最优控制实验表示为aRNA-MC-SMC-T。4组实验下控制器的参数均由同一种算法在相同参数平台获取,仿真时间为20 s,采样周期为0.001 s。

反义RNA膜计算优化算法的参数设置:G=100、L=5、C=10,其他参数设置与文献[16]相同,每组实验算法均独立运行20次,取最优结果作为最终结果。当进行PID闭环控制参数优化时,n=3,每个参数搜索范围均为[0,200];当进行滑模控制参数优化时,n=4,每个参数搜索范围均为[-10,200]。不同控制策略下的最优控制器参数、桥式吊车位置、摆角曲线分别如表1、图7和8所示。

表1 相同算法下不同控制策略获取的最优控制器参数

图7 相同算法下不同控制策略获取的最优参数的控制位置响应Fig.7 Position responses of optimal parameters obtained by the same algorithm with different control strategies

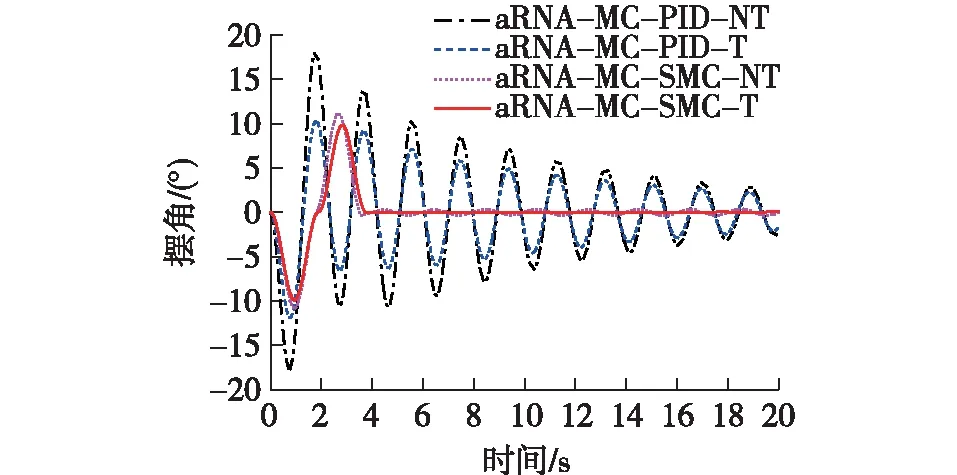
图8 相同算法下不同控制策略获取的最优摆角消除响应Fig.8 Optimal anti-swing angle responses obtained by the same algorithm with different control strategies

由图7和8可知:在相同参数优化算法下,无论目标函数改变与否,滑模控制较PID控制在位置控制中的上升时间和调节时间上均更短,在摆角消除过程中消摆更快,整体性能更加优异。这是因为PID控制器的线性控制特点很难有效地解决这类复杂非线性系统控制问题。此外,aRNA-MC-SMC-T在桥式吊车位置控制和摆角消除两方面与aRNA-SMC-NT相比,前者的综合性能更好,尤其是aRNA-MC-SMC-T对摆角消除有较大改善(4 s后吊绳摆动几乎完全消除)。

3.2 相同评价函数下不同算法比较

无论是经典的PID控制还是滑模控制,摆角和吊车位置之间的耦合使得控制器的参数整定变得尤为困难,为防止笔者所提算法较差的搜索性能对消摆控制的影响,基于相同的实验环境、消摆策略和目标函数,将笔者所提反义RNA膜计算优化算法与文献[12]所提动态差分进化(DDE)、文献[20]所提PID算法结果进行对比。反义RNA膜计算优化算法参数设置与第3.1节一致,PID[20]、DDE-PID[12]、SMC[12]、DDE-SMC[12]与笔者所提优化算法aRNA-MC均在a(t)=1、b(t)=2所形成的相同评价函数控制要求下,再次进行结果对比和验证。不同算法所得最优控制器参数、吊车位置、摆角曲线分别如表2、图9和10所示。

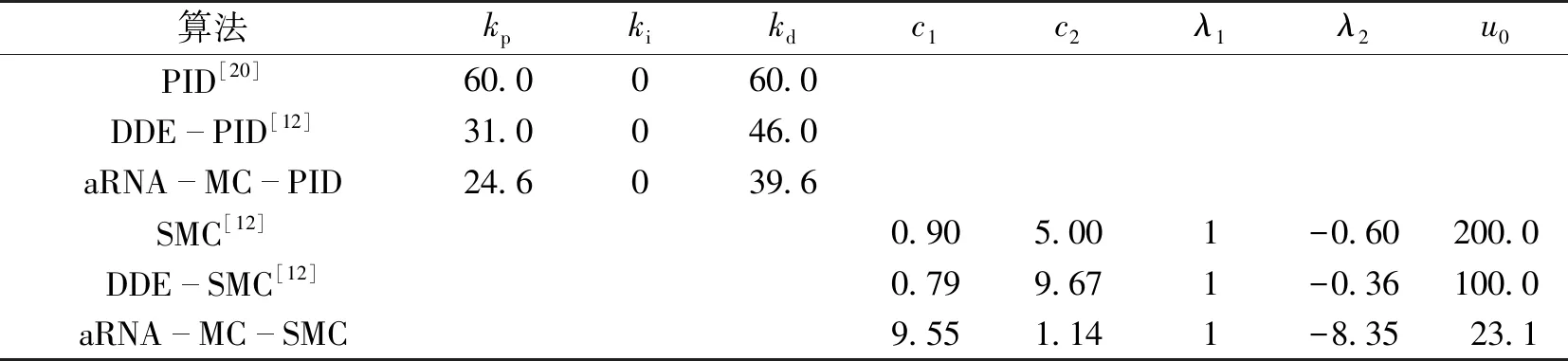
表2 相同评价函数下不同算法获取的最优控制器参数

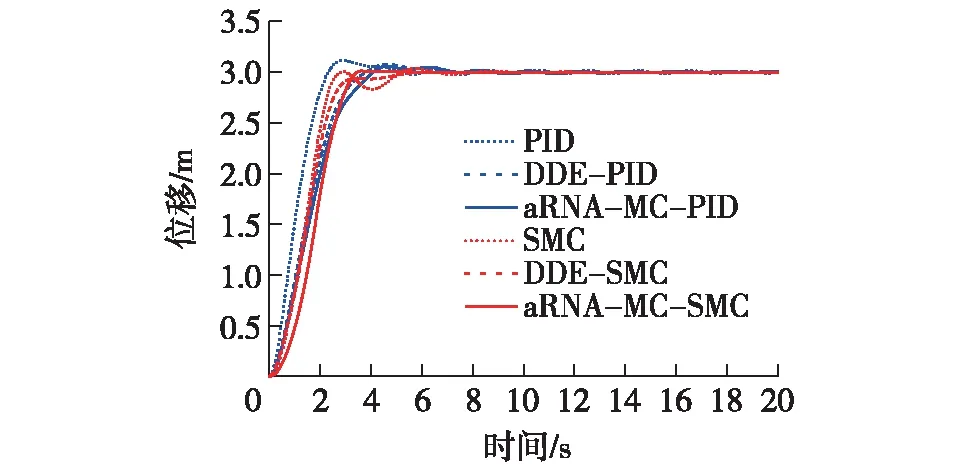
图9 相同评价函数下不同算法获得的最优参数的控制位置响应Fig.9 Position responses of optimal parameters obtained by different algorithms with same evaluation function

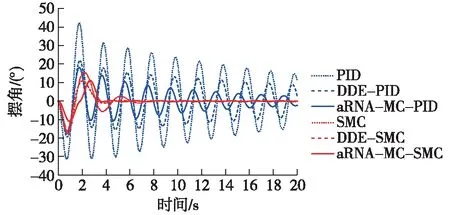
图10 相同评价函数下不同算法获得的最优摆角消除响应Fig.10 Optimal anti-swing angle responses obtained by different algorithms with same evaluation function

由图9和10可见:相同评价函数下进行不同控制器的参数优化结果表明,DDE-PID(蓝色虚线)与DDE-SMC(红色虚线)的最优消摆性能存在差异,这再次印证了滑模控制器的优势。PID这类线性控制器对桥式吊车控制效果不理想,且控制性能受负载重力的影响较大。主要原因是其自身的线性控制特点使得单纯的PID控制策略很难有效地解决这类复杂非线性系统控制问题。在负载摆角抑制上,基于笔者所提出的aRNA-MC-PID摆角消除响应(蓝色实线)较PID[20](蓝色点线)和DDE-PID[12](蓝色虚线)的摆角响应消摆更快。而基于笔者所提出的aRNA-MC的滑模控制(红色实线)也较SMC[12](红色点线)、DDE-SMC[12](红色虚线)的控制性能更为优越,在aRNA-MC-SMC的控制下,实验所讨论的欠驱动桥式吊车在更短的时间内实现了更加理想的搬运过程。

针对笔者所研究的这一类欠驱动桥式吊车最优消摆控制,基于反义RNA膜计算(aRNA-MC)优化算法的欠驱动桥式吊车系统滑模最优消摆控制性能更优,可更加高效地避免负载运输过程中的安全问题。