基于时变和动力耦合作用的钢管混凝土拱桥受力性能研究

汪继文 叶惠忠 潘兴虎 周愉涛 卢彭真

摘要：为了解时变和动力效应耦合作用下的钢管混凝土拱桥的受力性能，文章以跨径布置为（30+80+30）m的某钢管混凝土拱桥为依托工程，采用数值积分和有限元方法，建立较为精确的空间有限元模型，系统地研究大跨度钢管混凝土拱桥结构在动力和时间效应耦合作用下的受力性能。分析结果表明：在收缩徐变和动力效应的耦合作用下，钢管混凝土拱桥的受力更为复杂，其内力值较未考虑耦合作用的情况大，且放大效应较明显，因此在钢管混凝土拱桥的结构设计和验算中应充分考虑时变和动力效应的耦合作用。

关键词：钢管混凝土拱桥;有限元分析;时间效应;动力效应;受力性能

0 引言

钢管混凝土拱桥具有施工快、承载力好、经济效益高等优点[1]。近些年来，不少学者对大跨度钢管混凝土拱桥的时间效应及动力效应展开了较为深入的研究;王元丰[2-3]和泮以龙[4]等分别对钢管混凝土构件和钢管混凝土拱桥的徐变进行了研究;王少钦等[5]对移动车辆作用下桥梁的动力反应进行研究;李清海等[6]研究了在车辆荷载作用下桥梁结构力响应问题。现有研究成果中多是将收缩徐变和动力效应对结构承载力影响分开考虑，并研究各自的处理方法，而忽略了对时变和动力效应耦合作用下的受力性能的研究。然而由于钢管混凝土拱桥在实际运营过程中会受到钢管混凝土的收缩徐变和车辆移动荷载的同时作用，这二者之间是否会发生耦合效应，甚至加速拱桥劣化，尚处于研究的空白区域。

针对上述问题，本文依托永宁江2号大桥工程，通过对比分析选择较为合适的收缩徐变预测模型，并以此建立ANSYS全桥模型，模拟分析该桥十年以内的混凝土收缩徐变下的位移，并分别对其核心混凝土和钢管应力变化进行了研究。

1 工程概况及有限元模型的建立

永宁江2号大桥为飞鸟式钢管混凝土拱，桥跨径布置为（30+80+30）m，全宽64.6 m;80 m中跨采用中承式钢管混凝土拱肋，拱轴线采用二次抛物线线形;拱桥矢高为20 m，矢跨比为1/4，净跨径为74.75 m;拱肋截面呈宽哑铃形，其中钢管和平联壁厚为24 mm，钢管内部填充C50微膨胀混凝土。[=XQS（]基于时变和动力耦合作用的钢管混凝土拱桥受力性能研究/汪继文，叶惠忠，潘兴虎，周愉涛，卢彭真[=JP2] 本文采用ANSYS15.0软件建立了钢管混凝土拱桥的有限元模型，对其拱肋核心混凝土进行了成桥十年内的收缩徐变效应模拟计算。借鉴以往钢管混凝土拱桥有限元建模方法[1，7]，本研究采用Beam188空间梁单元模拟主拱肋钢管及混凝土、横梁、纵梁、风撑、立柱等结构，采用link8单元模拟拱桥的系杆和吊杆之间的联系，而立柱和横梁之间的联系则采用combine14模拟。钢管和混凝土单元均采用共节点的形式建立。其中钢管和核心混凝土的弹性模量分别采用实际的材料特性，保证截面应力非平均化，以真实反映截面的实际受力状态。全桥模型如图1所示。

式中：徐变应力为σc（t）=σ（t）-σc（τ0），E′（t，τ0）为按龄期调整的有效模量;E′（t，τ0）=E（τ0）[1+χ（t，τ0）φ（t，τ0）]，χ（t，τ0）为老化系数，建议取0.8。

为准确模拟钢管混凝土的收缩徐变，根据该拱桥所在地的全年气候条件信息，在融合上述收缩徐变公式的精细化模型中，设置该钢管混凝土拱桥全年平均湿度RH=80%，年平均气温为17 ℃，最高气温和最低气温分别为40 ℃和-7 ℃。

本文着重分析汽车过桥时桥面及拱肋的竖向位移、弯矩及轴力的时程反应。分别计算汽车以3.6 km/h、18 km/h、36 km/h、72 km/h的速度通过桥面时桥梁的竖向动力响应，并且考虑收缩徐变的影响。当移动荷载速度v=3.6 km/h时，基本不会引起桥面的振动，可近似视为桥面承受静载作用。

考虑到动力效应下结构的动弹性模量与静弹性模量的不一致性，参考文献[9]中的研究，在建模中考虑钢管内填混凝土的动弹性模量为静弹性模量的1.14倍。然而这只是根据先验理论的一种估计，有关动力与时间效应耦合作用下动弹性模量与静弹性模量之间关系的研究仍需进一步开展。

3 控制截面变形

在不同速度和收缩徐变下拱顶位移峰值和跨中位移峰值如表1所示。

由表1可知，随速度的增大，位移变化规律比较复杂：拱顶位移先增大后减小，而跨中位移则持续增大，且在速度为72 km/h时达到峰值;同时，随收缩徐变时间的增长，位移均逐渐增大。可见动力作用会对位移产生一定的放大效应。4 控制截面内力

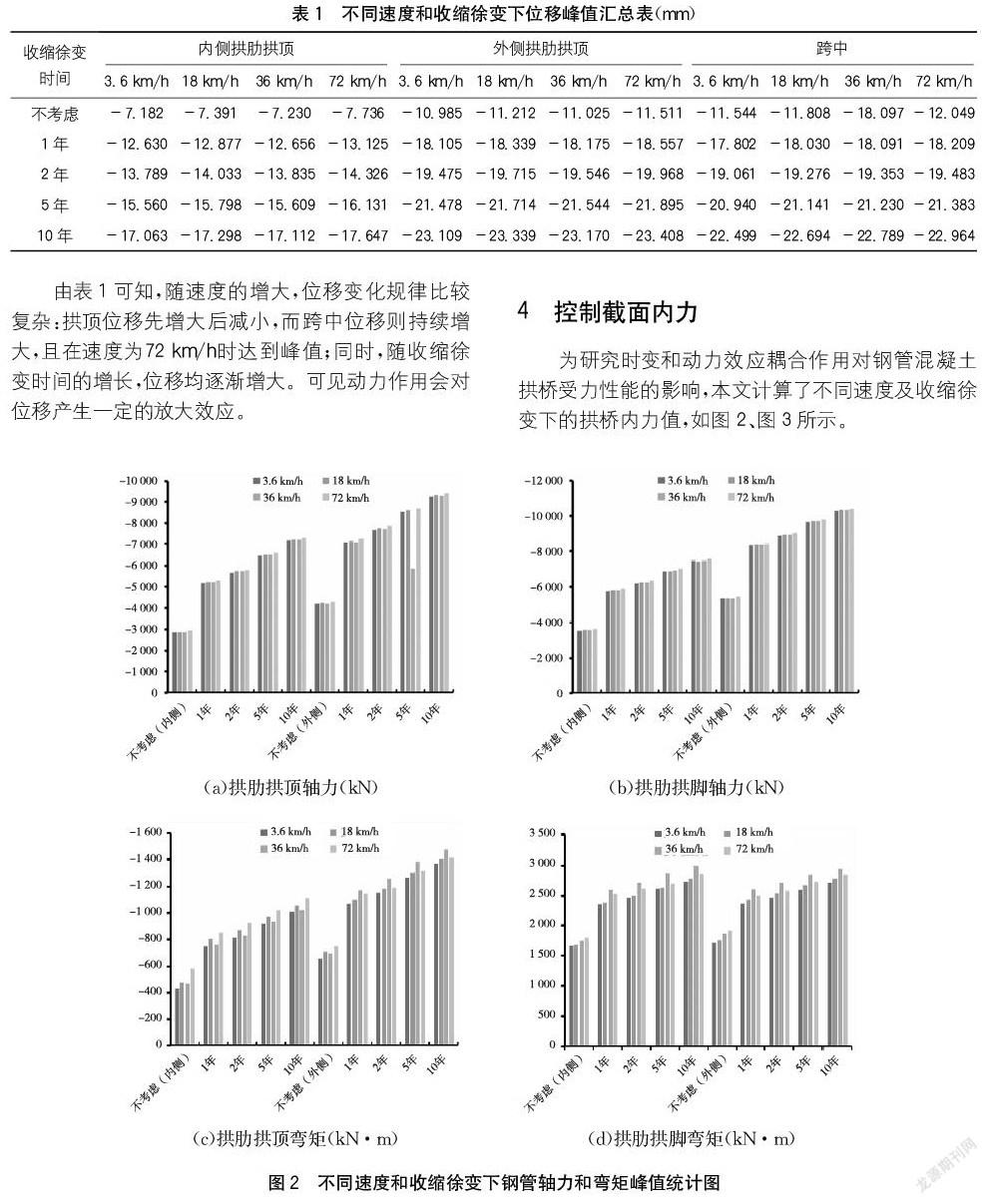
为研究时变和动力效应耦合作用对钢管混凝土拱桥受力性能的影响，本文计算了不同速度及收缩徐变下的拱桥内力值，如图2、图3所示。

由图2～3可知，随速度的增大，内力均较静载作用下的内力值大;随收缩徐变时间的增长，钢管内力增大，混凝土除拱顶弯矩外均减小。随速度的增大，动力和徐变耦合作用对内力会产生一定的影响。当移动荷载速度逐渐增大时，拱肋的动力效应基本呈现放大的趋势。

内外侧吊杆N2軸力峰值如表2所示。

由表2可知，随速度的增大，内侧吊杆N2内力增大，外侧吊杆内力则先增大后减小，但均比静载下的内力大，增长幅度峰值达7.8%，对内力的放大效应较显著。随收缩徐变时间的增长，吊杆内力变化比较复杂，但总体而言其对吊杆内力的影响较小。

5 结语

本研究建立了永宁江2号大桥的有限元模型，分析该桥十年内的混凝土收缩徐变下的位移，及其核心混凝土和钢管应力变化，得出了如下结论。

（1）随着速度的增大，钢管混凝土拱桥的位移、内力变化规律较复杂，但均较静载下的位移、内力要大。其中拱顶位移先增大后减小，跨中位移则持续增大，且在速度为72 km/h时达到峰值;内侧吊杆N2内力增大，外侧吊杆内力先增大后减小，但均较静载作用下的内力大，增长幅度最高可达7.8%，对内力的放大效应显著。

（2）随着收缩徐变时间的增长，钢管和混凝土位移均增大;同时，钢管内力增大，而混凝土除了拱顶弯矩外均减小;拱桥的吊杆内力变化较复杂，但就分析结果而言，收缩徐变对吊杆的内力影响较小。

（3）收缩徐变和动力耦合作用会对拱肋位移和内力产生一定的影响，随着速度的增大这种增幅效果将会越明显。在钢管混凝土拱桥的结构设计和验算中应充分考虑行驶车辆的车速问题，在必要时应予以限速。

（4）未来的工作仍需围绕以下两部分开展：①根据实验结果建立动力与时间效应耦合作用下动弹性模量与静弹性模量之间的新型关系模型;②实验和模拟分析结合，确认行车因素（荷重、累计作用次数、幅值、组合材料面积）对收缩徐变的影响。

参考文献：

[1]张德生，李远瑛，刘 洋.钢管混凝土拱桥静载试验与有限元分析[J].混凝土，2005（8）：64-66.

[2]刘可为，王元丰，韩冰.钢管混凝土框架结构的徐变分析[A].中国钢结构协会钢-混凝土组合结构分会第十次年会论文集[C].中国钢结构协会钢-混凝土组合结构分会：中国钢结构协会钢-混凝土组合结构分会，2005.

[3]周 耀，王元丰.考虑徐变的钢管混凝土拱桥动力分析[J].大连理工大学学报，2006（S1）：82-87.

[4]泮以龙，卢彭真，曾 新，等.考虑收缩徐变的钢管混凝土拱桥稳定性参数分析[J].山东交通科技，2019（5）：53-54，67.

[5]王少钦，岳祖润，马 骎.车辆对桥梁动力作用简化方法的研究[J].石家庄铁道学院学报，2005（3）：47-51.

[6]李清海，谭笃光.车辆荷载作用下桥梁动力效应的有限元分析[J].振动与冲击，1994（1）：15-22.

[7]林春姣，林春伟，欧 伟.新型哑铃型钢管混凝土拱肋施工阶段水化热温度试验研究[J].混凝土，2011（8）：138-139，143.

[8]陈扬瑞，曾 新，朱明礼，等.混凝土徐变对钢管拱桥受力性能的影响[J].北方交通，2019（11）：1-4，9.

[9]王佳雯.混凝土抗压强度与动弹性模量关系试验研究[D].武汉：湖北工业大学，2017.