基于广义Choquet积分的职位推荐算法
2021-01-20陆佳雯雷志丹朱儒康
陆佳雯,武 频,雷志丹,朱儒康
(上海大学 计算机工程与科学学院,上海 200444)
0 引 言
传统线下招聘模式因成本高,效率差逐渐被线上招聘模式所取代。目前网站招聘推荐内容主要以目标职位精准性为主,推荐的职位类别相对狭窄[1]。根据求职者自身技能性质以及对岗位的要求,本文将通常概念的求职者分为两大类:专业型人才和通用型人才。专业型人才指通常有着明确的行业方向意愿,从事职业对专业技能要求高的人群。通用型人才从事的职位通常对专业技能要求不高,且这类人群跨行就业率高,如快递员、保洁和导购等等。传统的推荐算法针对专业型人才有着不错的推荐效果,而对于通用型人才,推荐结果准确率不高且岗位多样性不足。
如广泛使用的协同过滤推荐算法[2]通过分析用户历史评分情况,由于职位推荐数据集缺乏评分等反馈信息,所以该方法不适合人才岗位匹配型数据。基于内容的过滤推荐[3-5]通过抽取物品属性进行特征学习,但是没有考虑到求职者本身的属性特征对择业心理的影响。
针对传统方法无法根据通用型人才这类人群本身的特点来实现多样性、有效性的职位推荐的问题,本文算法从求职者本身的特点出发,在人口统计学数据的基础上,利用层次分析法构建用户属性的层次结构模型并量化,用广义Shapley函数与离散Choquet积分相结合的方法计算相似人群的最终评分,根据相似人群列表来进行职位推荐。该方法能有效缓解冷启动问题,实现对通用型人才多样及有效的职位推荐。
1 相关工作
1.1 基于人口统计学数据的推荐
基于人口统计学数据的职位推荐将用户本身非敏感的个人基本信息融入到相似人群的计算当中,建立用户特征模型,得到最近用户邻集,最后系统将邻集中评分高的职位进行推荐[6]。基于人口统计学数据的推荐相比其它的推荐算法,有以下几方面优势:
(1)有效缓解冷启动问题。初次使用系统的用户根据自身的属性进行分析推荐,这些属性不会因没有使用记录而缺失;
(2)不依赖用户本身的数据。这个方法具有领域独立性,可以应用在不同的领域。在一些特殊的领域,像音乐、电影以及职位的推荐,邻近用户的不同喜好及经历不同,传统的协同过滤方法不能有针对性的推荐。
加入人口统计学数据的推荐算法,弥补了传统推荐算法的一些缺陷。通过加入用户本身的属性特征,计算相似人群,综合考虑了通用型人才这类人群的相似属性特征对择业心理的影响,实现推荐的多样性。本文利用层次分析法,对人口统计学数据进行量化处理[7],并使用广义Shapley函数和人口统计学数据计算用户间的相似度,最后利用逐级离散Choquet积分自下而上计算最终的模糊综合评分[8],将最终评分列表的TOPN个用户对应的职位列表推荐给当前用户。
1.2 λ-模糊测度和广义Shapley函数
传统的赋权方法大多存在着主观因素强的问题[9,10]。在利用AHP算法对用户指标进行重要度计算时,指标之间可能存在非独立性依赖关系。传统的可加测度虽然考虑到指标本身的重要性,却忽视了两两组合时的联合重要度。为了解决上述问题,本文将专家对应指标给出的权重通过公式计算出指标间的模糊测度,然后通过广义Shapley函数求得最优权重。
定义1λ-模糊测度[11]:设P(X) 是非空集合X={x1,x2,…,xn} 的幂集,给定λ∈(-1,∞),μ∶P(X)→[0,1], 如果满足以下条件则称μ是X上的λ-模糊测度:
(1)μ(∅)=0,μ(X)=1
(2)∀A,B∈P(X), 若A⊂B, 则μ(A)<μ(B);
(3)μ(A∪B)=μ(A)+μ(B)+λμ(A)μ(B), 其中λ∈(-1,∞)。
λ模糊测度可以理解为属性集A的重要程度。若λ=0即μ(A+B)=μ(A)+μ(B), 则μ是X上的可加测度,表示A和B之间是相互独立的;若λ<0,μ(A∪B)<μ(A)+μ(B), 则μ是X上的次可加测度,表示A和B之间存在冗余关系;若λ>0,μ(A∪B)>μ(A)+μ(B),则μ是X上的超可加测度,表示A和B之间存在互补关系。在多指标决策问题当中,λ-模糊积分能实现更精准表达指标间的复杂相互影响关系。
定义2 广义Shapley函数[12]:在决策过程中,由于指标间存在关联关系,指标集S∈P(X) 的重要度不仅与自身有关系,还要考虑到其它指标。Shapely函数在博弈论领域中被广泛研究。由于模糊测度μ是基于幂集的,所以一般的模糊测度增加了计算广义Shapley值的复杂度。为了降低计算复杂度,本文利用λ-模糊测度来替换一般模糊测度。综合考虑指标集S的重要度。广义Shapley值定义如下
(1)
其中,X是所有指标 {x1,x2,…,xn} 的集合,S是X的任意一个子集,XS表示X的差集,n,t和s分别是N,T和S的基数,μ是X上的模糊测度。
由式(1)可知,如果S={i}, 则
(2)
2 算法设计
本文利用相似人群来进行职位推荐,相似人群选择的有效性对后期推荐的精度有直接影响。传统的协同过滤算法会受数据量大的影响而增加数据稀疏的概率。本文通过基于人口统计学数据和广义Choquet积分的层次分析法来计算用户相似度,融入用户个人基本属性可以反映用户特征及兴趣偏好,具体算法流程如下:
步骤1 建立评估目标的递阶层次结构
该步骤主要是剖析复杂系统的过程,将目标的注意力放在层次结构的顶层且顶层仅有一个元素,下层元素的个数不定。评估目标的基本层次结构包含3层,从上往下依次是目标层、准则层以及指标层,这是基于逐层分解的思想而建立系统的评估体系。根据用户在职位选择过程中的影响因素,本文将用户指标定为个人信息相似度及能力相似度这两个准则,个人信息相似度准则包含的指标有年龄、性别、最高学历、专业和城市,能力相似度准则包含的指标包括求职意向、历史职位、工作经验(时间)。构造的层次结构如图1所示。
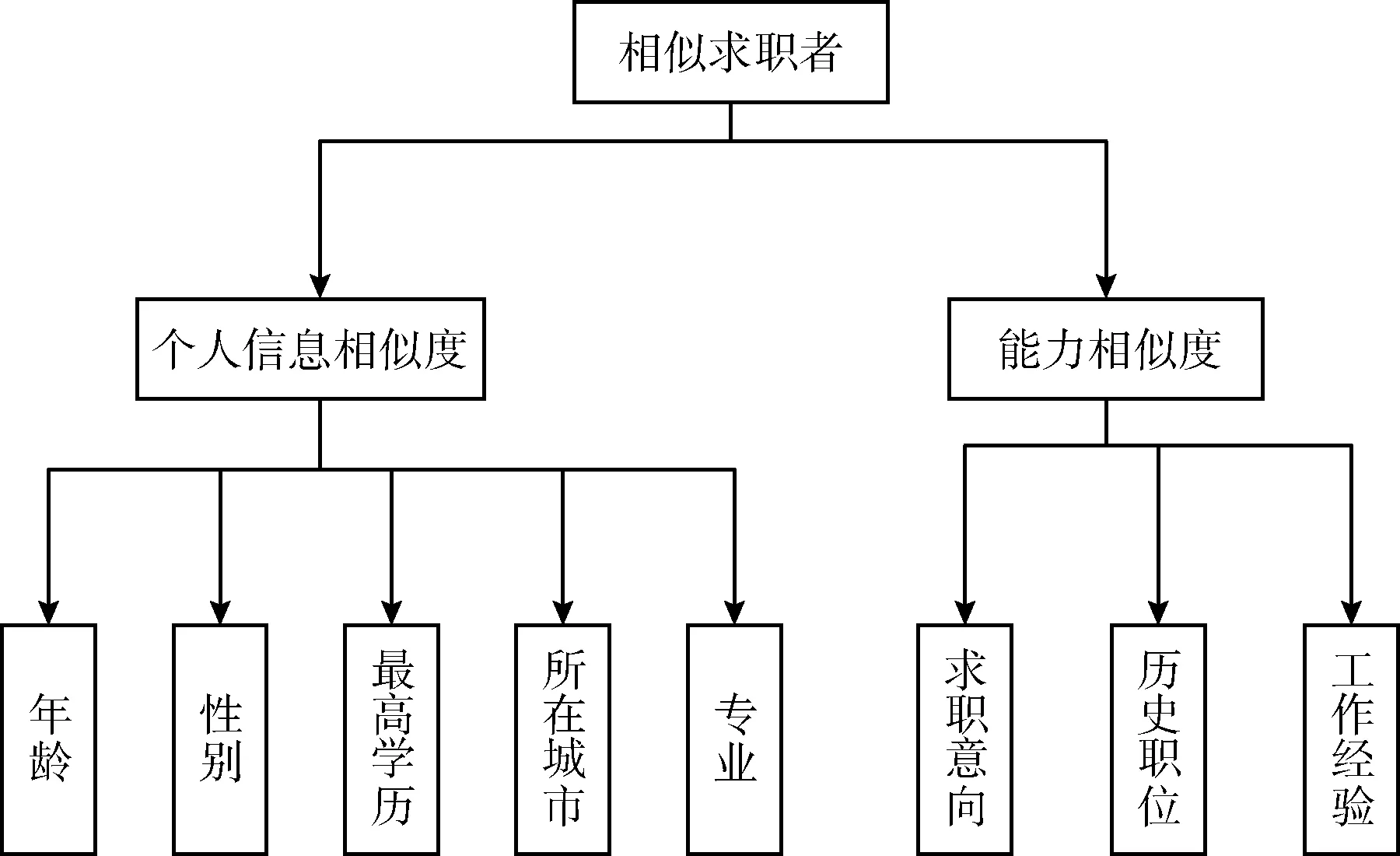
图1 层次结构模型
步骤2 计算模糊测度及Shapley值
以图1中个人信息相似度指标为例,其对应有5个评估指标:年龄C1, 性别C2, 最高学历C3, 城市C4, 专业C5。 通过专家对应5个指标构造判断矩阵,即任意两因素之间的重要程度比值。对比矩阵如下
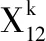

表1 1~9数量标度
上诉构造的判断矩阵不一定满足一致性,例如C1∶C2=2∶1,C2∶C3=3∶1,C1∶C3=5∶1 (如果满足一致性应该为6∶1)。当CR小于0.1时则认为该判断矩阵具有一致性。如果满足一致性,那么最大特征值所对应的特征向量即为各指标对应的权值。一致性可通过计算一致性比率CR来判定,由式(3)表示
CR=CI/RI
(3)
其中,RI大小为固定值,它和矩阵的阶数n有关,具体数值见表2。

表2 RI指数对照
CI计算公式如式(4)所示
(4)
其中,n为判断矩阵的阶数,λ是最大特征值。由最大特征向量得到各指标的权值μ=(μ(C1),μ(C2),…,μ(Cn))。 考虑到指标之间的联合重要度。令μ(Ci) 是Ci的权值,P(C) 是C={C1,C2,…,Cn} 的幂集。基于λ-模糊测度,一些学者[12]给出了计算μ(A)(A⊆C即∀A∈P(C)) 的方法,模糊测度公式如下
(5)
尤其当A=C时,μ(A)=μ(C)=1。 因为集合C={C1,C2,…,Cn} 存在关联关系,所以有下式成立
(6)
将每个指标对应的权值代入式(6)求得λ的值,再将所求λ值代入式(5),可以分别求得C={C1,C2,…,Cn} 各指标子集的模糊测度。根据式(1)、式(2)以及得到的各指标子集的模糊测度,进一步计算得到各指标的广义Shapley值作为指标最终权重。
步骤3 相似度计算
求职者间的指标相似度F={f(c1),f(c2),…,f(cn)} 计算包括数值型数据和字符型数据,指标间相似度的度量f(ci)=sim(x,y) 应该具有以下几个特性:
(1)对称性:sim(x,y)=sim(y,x);
(2)等价性:sim(x,y)=1,sim(y,z)=1, 那么sim(x,z)=1;
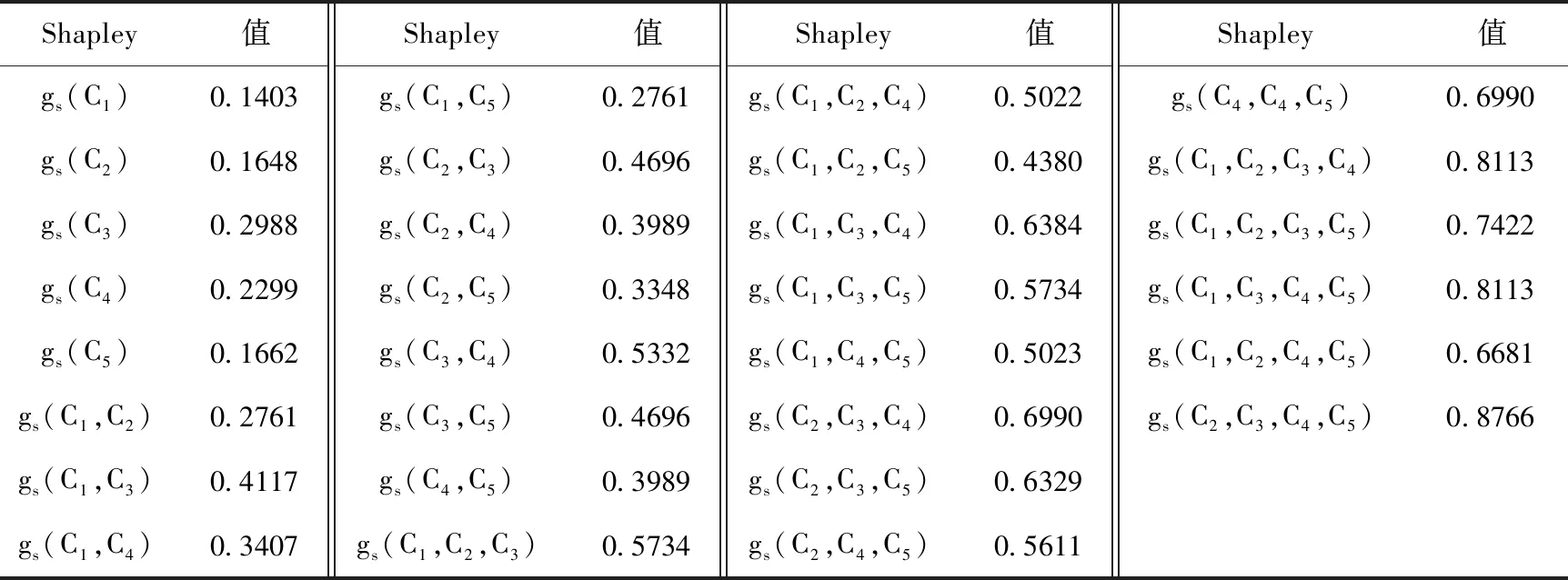
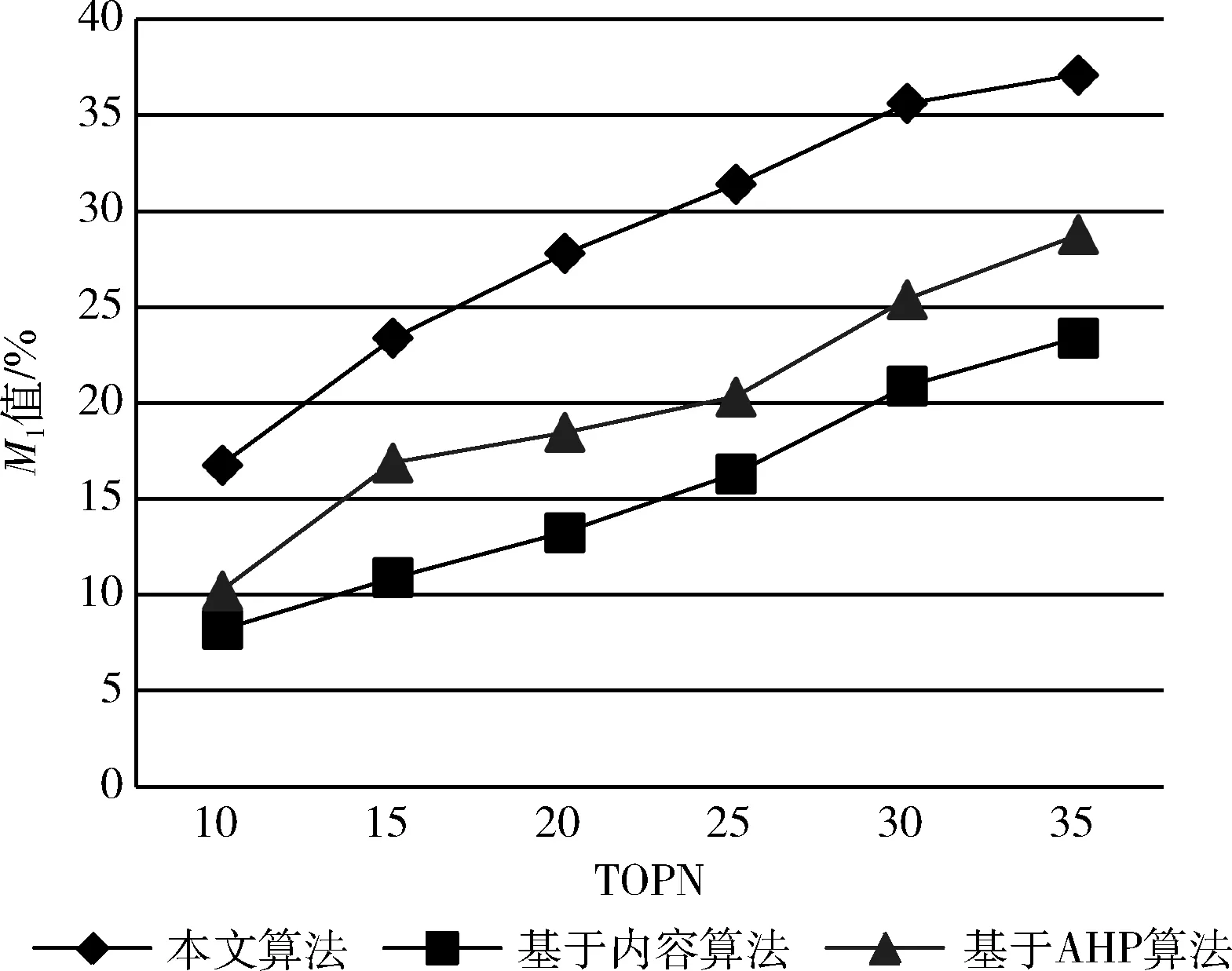
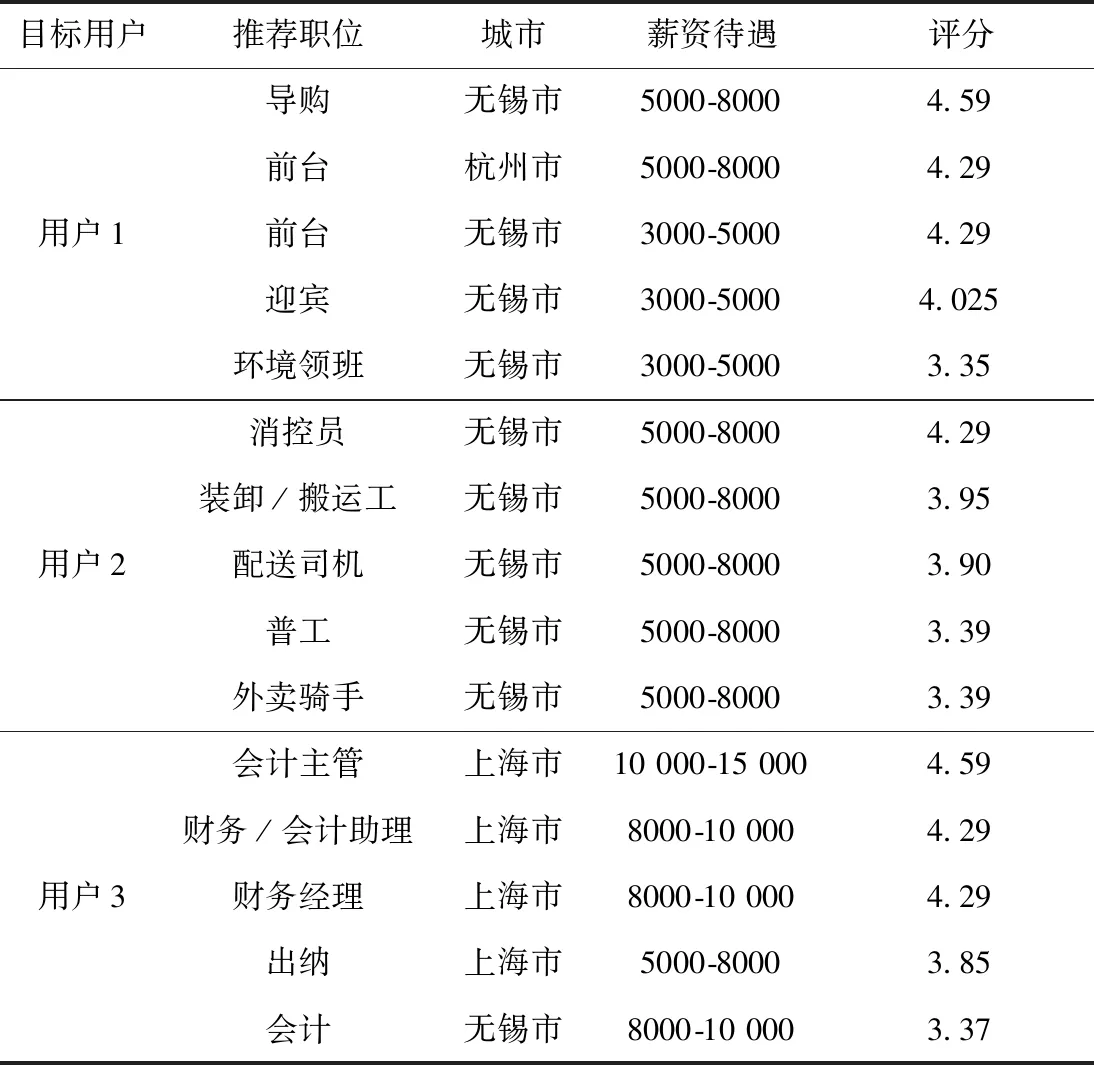
(3)非负性: 0 局部相似度计算公式见表3。 表3 具体局部相似度计算公式 步骤4 求综合评估结果 每个用户最终相似度评分通过离散Choquet积分公式计算得出。设 (X,F) 是可测空间,μ∶F→[0,+∞] 上的非负单调集函数,且μ(∅)=0,f是空间上的非负可测函数的集合。f关于μ的积分定义为 (7) 其中,Fα={ci|f(ci)≥α,ci∈C},C={C1,C2,…,Cn},α∈[0,∞)。 设μ为P(C) 上的模糊测度。f(Ci) 表示函数f(C) 在点Ci处的值,令W={f(C1),f(C2),…,f(Cn)},W中的函数值按升序排列,表示形式如下 上述条件成立,式(7)可以变形如下 (8) 基于底层的广义Shapley的模糊测度和相似度数值,通过Choquet积分自下而上逐级求得评估结果。将得到的TOPN个相似用户的对应数据库中的职位列表推荐给当前用户。 实验数据是由招聘公司提供的真实的招聘匹配信息,包括3217条职位-求职者匹配信息、2041条公司信息、12 335 条求职者信息、5519条职位信息。以这些数据的匹配信息作为实验数据集。 实验结果通过计算准确率、召回率来衡量。其中,L(v) 表示通过上述算法为求职者v推荐的职位列表。Mv表示职位录取的求职者列表 根据准确率和召回率计算调和平均值M1, 公式为 本文依据图1并参考招聘公司专家给出的评价矩阵得到C={C1,C2,…,C5} 各指标的权重向量μ1=(0.2,0.3,0.5,0.4,0.3)T, 考虑到指标之间的关联关系,由式(6)可以得到 从而得到λ=-0.804。 同理,对于能力相似度准测的指标:求职意向C6, 历史职业C7, 工作经验C8赋予权重向量μ2=(0.6,0.4,0.4)T, 可得λ=-0.698; 目标层的指标:个人信息相似度C9, 能力相似度C10赋予权重μ3=(0.5,0.6), 可得λ=-0.33。 根据式(5)获得每个指标子集的模糊测度,根据式(2)进一步计算各指标子集的广义Shapley模糊测度,以个人相似度指标为例,其各指标子集的广义Shapley值见表4。 表4 个人相似度各指标子集的广义Shapley值 在求得各层的广义Shapley值与表3中的相似度计算公式的基础上,根据式(8)离散Choquet积分公式,逐层计算Choquet积分,得出相似用户列表。 图2展示了调和平均值的对比结果,通过利用众和雷达招聘网站提供的真实招聘数据来计算推荐成功率,将结果与传统推荐算法进行对比。发现本文提出的基于人口统计数据和广义Choquet积分的职位推荐算法在TOPN的各个取值中都有更好的效果。面对通用型人才这类跨行就业率高的人群,传统推荐算法很难通过计算职位的精准性来满足求职者的择业心理。当N取值较小时其推荐效果仍然优于另外两种算法,因为在计算时融合了人口统计学数据与广义λ-Shapley Choquet积分,很好弥补了权重赋值的主观性并考虑了指标间的关联关系,且有效缓解了冷启动问题。当N的取值越大时,推荐效果也越好。这是由于对于通用型人才来说,择业没有一个固定的行业意愿,受不同岗位待遇的影响较大,跨行就业率高。传统职位推荐算法从追求岗位推荐的精准性方面很难满足这类人群的需求。从图2中可以看出,当N的取值达到35时,本文提出的职位推荐算法M1达到了37.1%,传统的基于AHP的推荐算法为28.75%,而基于内容的推荐算法仅为23.4%,M1值至少提高了8.35%。由此验证了融合广义Shapley函数和Choquet的层次分析法的职位推荐算法要比单独考虑一种因素的算法效果好得多,这也验证了本文算法的有效性。 图2 3种算法调和平均值比较 在职位推荐高有效性的前提下,为了更直观地展示为通用型人才在职位推荐时的岗位多样性,选取了表5中3个具有不同属性特征的人群代表,用户1和用户2属于通用型人才,这类人群在求职时会更关注工作地点以及薪资待遇,且同类别人群跨行就业概率大,所以表6通过计算相似人群来获取的推荐结果呈现出推荐岗位的多样性。同时,通过相似人群的共同特征来获取的职位推荐列表也为求职者提供了潜在职业的可能性。而用户3属于专业型人才范畴,由于这类人群本身在求职时有明确的目标岗位,推荐结果的行业跨度不如前两者来得大,这样也满足了这类人才在求职时的行业需求。 表5 待推荐目标求职者 表6 目标用户TOP-5职位推荐 本文提出了一种基于人口统计学数据和广义Choquet积分的职位推荐算法,结合了非可加测度与广义λ-Shapley Choquet积分对传统的层次分析法进行优化,对相似用户进行排序和择优。区别于传统基于内容的推荐算法,本文充分考虑了通用型人才这类人群在择业时考虑的外在因素,算法从个人基本信息相似度和能力相似度出发,考虑了年龄、性别、最高学历、专业、城市、求职意向、历史职业、工作经验这几个指标,利用改进的层次分析法将个人属性进行量化,由专家给出每个指标的重要度,利用广义Shapley函数计算出指标之间的最优模糊测度。最后利用Choquet积分从下而上逐层计算得出最终的模糊综合评分,选取TOPN个用户ID,在用户库中查询对应的职位列表进行推荐。 该方案有效处理了不同指标之间的关联关系,弥补了传统推荐算法中职位推荐范围局限、无法融合求职者本身的属性特征、挖掘潜在职业可能性的问题。因而具有很强的可操作性以及实用性。实验结果显示,对比传统的基于内容或者基于AHP的推荐算法,本文提出的职位推荐算法效果对于通用型人才人群更佳。为推荐算法的应用研究提供了参考。融合职位的流行度走势进行职位推荐是下一步的研究方向。
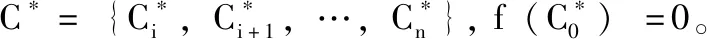
3 实验结果
3.1 实验数据集
3.2 基于人口统计学与广义Choquet积分的推荐实验结果

4 结束语
